[Перевод] Простое и строгое доказательство 26/10 измерений в теории струн14.09.2020 12:03

yvhlds5br-74hqh3uwgt0y3oxna.jpeg

… вы нигде не найдете.

По крайней мере, у меня не получилось сделать его таковым. Требование определенного и большого числа пространственно-временных измерений (26 для более простой бозонной теории струн и 10 для более сложных суперструн) это один из наиболее неправильно понимаемых аспектов, который, собственно, является основным источником негативных чувств к данной теории. Придется очень постараться, чтобы объяснить происхождение этих странных чисел неспециалистам.

Строго говоря, действительно магическим числом является не сама D-мерность пространства-времени, а D−2 измерений, поперечных струне, в которых она может колебаться (минус один для измерения времени и минус один для измерения, продольного струне). Другими словами, 1D-струна образует в пространстве-времени 2D-поверхность, называемую мировым слоем. Магическое число — это число оставшихся направлений, доступных для струны. Так и выходит D-2.

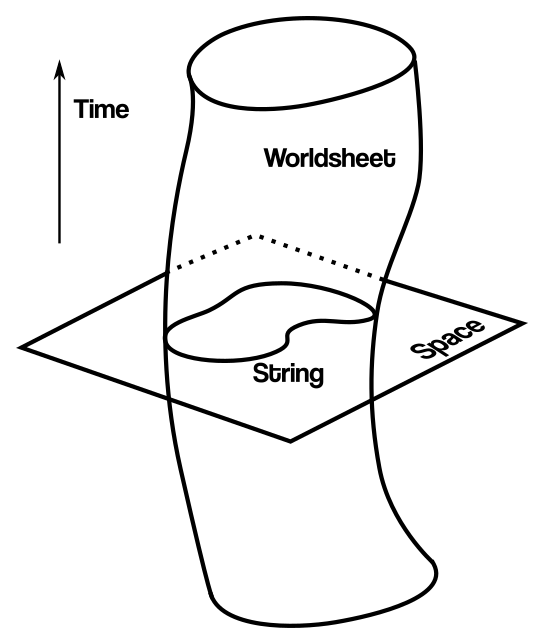
he_cwkzylxgzmyd78civ3ummz8e.png
Эта картинка была плохо нарисована по крайней мере тысячу раз, так что пусть будет еще одной плохой картинкой больше

24-поистине мистическое число. Джон Баэз дает фантастический отчет о том, почему его любимое число именно 24 — которое является одним из драгоценных камней разбросанных по математике. Некоторые из них выглядят абсолютно ничем иным, как чистой нумерологией:

$ 1^2 + 2^2 + 3^2 + \ldots + 23^2 + 24^2 = 70^2 $

и это работает только для 24, за исключением 0 и 1, конечно. (Если вы любите сложные математические головоломки, попробуйте доказать это. А я не буду). И уж совсем невероятно, как это забавное тождество связано с неожиданно сложной и увлекательной (чудовищно вздорной) математикой и теорией струн (которая действует как «клей» для чудовищного вздора). Немаловажное значение имеет рождение 24/2 из ряда:

$$display$$ 1 + 2 + 3 + 4 + \ldots »=» -\frac{1}{12} $$display$$

Собственно, именно поэтому в бозонной теории струн D-2=24. В суперструнах эквивалентным безумием будет:

$$display$$ 1 — 2 + 3 — 4 + \ldots »=» \frac{1}{4} $$display$$

что дает D-2=8. В конце концов, это звучит как случайные несвязанные факты (и «факты» в кавычках), и хотя каждый из них может быть легко объяснен непрофессионалу, я на самом деле не объясняю, какова должна быть связь с числом измерений в теории струн. Я кажусь сумасшедшим не потому, что говорю что-то неправильное, а потому, что эти вещи непоследовательны и бессвязны. Проблема в том, что соединительная ткань слишком сложна с технической точки зрения, и с математической, и с физической, и с психологической, — чтобы я мог ее просто объяснить.

Как с наименьшими возможными усилиями убедить кого−то, что D-2 = 24? Это намного проще, если этот кто-то принимает сумасшедшее уравнение 1+2+3+... = -1/12;, но это явно не удовлетворительно строго. Даже если это можно понять, например, с помощью ζ-регуляризации, то есть с регуляризацией теплового ядра + аналитической перенормировкой (и на этот счет уже есть много материала), то это все равно будет неудовлетворительно, поскольку нет никакой причины, по которой все эти манипуляции должны иметь какое-либо отношение к физике. Возможно ли прийти к правильным результатам без этого сумасшедшего уравнения; то есть, по сути, не сталкиваясь с какой-либо «нерегулярностью» для регуляризации? Да, конечно. Но как именно кратко и элементарно такое проделать?

Я обнаружил, что доказательства D=26 можно примерно классифицировать как:


  1. Квантование светового конуса
    • с сумасшедшим уравнением. Требуется немного знаний о поляризациях массивных / безмассовых векторных бозонов.
    • без сумасшедшего уравнения. Требуется, по существу, изучить все о квантовании струн / алгебре Вирасоро.
  2. Конформная теория поля
    • без сумасшедшего уравнения. Требуется знание конформных теорий поля и конформных аномалий.
  3. Модулярная инвариантность
    • с сумасшедшим уравнением. Требует довольно элементарной квантовой механики и математики.
    • без сумасшедшего уравнения. Требуется элементарная КМ, но с базовым нудным комплексным анализом.

Доказательство 1.1, я недавно привел здесь. Это довольно просто, но вы должны доверять сумасшедшему уравнению. Другое доказательство с сумасшедшим уравнением 3.1, находится в слайдах Баэза.

Доказательства, свободные от безумия, любопытным образом образуют нечестивую Троицу. Каждое из них требует знания только из одной вершины треугольника, который образуют:


  • Теория струн
  • Теоретическая физика
  • Математика

Доказательство 1.2 является наиболее распространенным во введении в теорию струн, так как вы уже изучаете необходимую физику струн в любом случае, и это математически не пугает. Доказательство 2.1 предназначено для более углубленного изучения и дает очень четкую физическую интерпретацию критического числа измерений, поскольку оно непосредственно связано с отменой конформной аномалии. Доказательство 3.2 я никогда раньше не видел — оно кажется идеальным для людей, которые знают что-то из базового комплексного анализа (теорема вычетов и все такое) и некоторые азы квантовой механики, что не требует почти никаких знаний о физике струн.

Я очень старался выжать простое доказательство, которое является «строгим» (не использует сумасшедшее уравнение), но у меня ничего не вышло. Я пришел к убеждению, что три вершины треугольника следует понимать как перевод на разные языки одного и того же концептуального ядра, и это ядро нередуцируемо. Так что если два звена в цепи доведены до минимальной сложности, то третьему приходится все это съедать.

Все, что у меня вышло — это следующая реализация доказательства 3.2. Оно отодвинет теоретическую и струнную физику на задний план и сосредоточит внимание на математике, то есть будет максимально строгим с математической стороны (хотя иногда будут замахи и на физику). Доказательство будет довольно длинным, но я нахожу его удовлетворительным. Мы соберем 24 по частям (как 2, умноженное на 3, умноженное на 4). Считайте это письмом с извинениями за освобождение 1+2+3+...=-1/12 в дикую природу.


Пруф

Мы уже говорили о мировой поверхности, которую струна образует в пространстве-времени. На этой поверхности мы можем установить систему координат $(\sigma^1,\sigma^2)$. Очевидно, что, хотя наблюдаемые могут быть записаны в терминах этих координат, они должны быть инвариантны при изменениях координат $(\sigma^1,\sigma^2) \rightarrow (\sigma^{1}\prime,\sigma^2 \prime)$. В конце концов, координаты изначально произвольны. Простым примером (локального) изменения координат является растяжение/масштабирование:

$ (\sigma^1, \sigma^2) \rightarrow (\lambda \sigma^1, \lambda\sigma^2) $

Итак, мы понимаем, что наблюдаемые в нашей теории должны быть инвариантны при таких масштабированиях. Это легко сделать классически, но становится очень нетривиальным, когда проблема переходит в удел квантовой механики. Эта масштабная симметрия является частью так называемой конформной симметрии мировой поверхности теории струн.

Представьте себе ситуацию, в которой струна делает петлю во времени, оставляя торовидный след в пространстве-времени. Конечно, множество возможных форм торов — это все равно правильный выбор. Мы хотим вычислить вероятность того, что этот процесс произойдет с определенной формой тора, или лучше, квантовой амплитудой, квадрат модуля которой является вероятностью. Основной момент квантовой механики состоит в том, что мы можем вычислить амплитуду, суммируя $exp(iE_it)$ по всем возможным состояниям i, каждое из которых имеет энергию $E_i$, через время t. таким образом,

$ Z = \sum_i e^{i E_i t} $

это общая амплитуда. Z должна удовлетворять нашим симметриям.

Важным моментом является то, что составная система AB из двух невзаимодействующих подсистем A и B имеет вид $Z_{AB} = Z_A Z_B$. Благодаря этому хорошему свойству мы можем сначала сосредоточиться на вычислении Z струны, колеблющейся в одном поперечном измерении, а затем возвести ее в степени D-2, чтобы заставить ее колебаться в поперечных измерениях D-2.

zf0i4lwnymks9-uopay04oyz5fk.jpeg
Подобно реальным вибрирующим струнам, струны теории струн имеют гармоники, которые являются целыми кратными фундаментальной.

Таким образом, струна почти точно похожа на настоящие гитарные струны и имеет бесконечные режимы колебаний, или гармоники, или обертоны. Каждая из них представляет собой гармонический осциллятор, который в квантовом варианте имеет энергетические уровни

$ E_n = \omega \left( \frac{1}{2} + n \right) $

Так ведь? Таким образом, Z одного квантового гармонического осциллятора будет

$ Z_{QHO} = \sum_{n=0}^\infty e^{i E_n t} = e^{\frac{i}{2}\omega t} \sum_{n=0}^\infty e^{i n \omega t} = \frac{e^{\frac{i}{2} \omega t}}{1 - e^{i\omega t}} $

Геометрический ряд, который я только что суммировал, кажется, имеет отношение |r| = 1, что означает, что он на самом деле не сходится. Давайте сорвем повязку прямо сейчас: такие вот Z, определенные наивно как у нас, почти никогда не сходятся в лоренцевой (то есть пространственно-временной) теории. Часто мы, физики, говорим, что они «осциллирующие», потому что мы суммируем кучу множителей exp (ix), а затем махаем руками, дескать, они каким-то волшебным образом отменяются, но это дешевая ложь — мы просто имеем в виду, что они не сходятся. Это справедливо не только в теории струн, но и для всей квантовой теории поля, или для стандартной квантовой механики, или даже для низкочастотного квантового гармонического осциллятора.

И что дальше? Правильней будет сделать время комплексной переменной. Придавая ему мнимую часть, мы заставим Z сходиться. Мало того: когда вы вычисляете из этого непосредственно наблюдаемые величины, а затем возвращаете t обратно к реальной оси, вы восстанавливаете разумные ответы (которые соответствуют эксперименту, когда это возможно). Итак, это не трюк; этот рецепт — наше определение того, что значит иметь квантовую теорию в пространстве-времени (не волнуйтесь, предположим, что t является сложным и в верхней полуплоскости Im t > 0.).

Чтобы вернуться в нужное русло, мы предположили, что одна струна в одном измерении имеет бесконечные моды колебаний, которые явно имеют частоты, кратные фундаментальной. На самом деле ω=1,2,3,… и поэтому Z для нашей 1D-струны является произведением

$ Z_{1,L} = \prod_{k=1}^\infty \frac{e^{\frac{i}{2}k t}}{1- e^{ikt}} = e^{\frac{i}{2} (1+2+3+\ldots)t } \left(\prod_k 1- e^{ikt}\right)^{-1} $

… и со всего размаху бухаемся на дно. Безумие 1+2+3+ … вновь настигло нас. Если бы мы были слабы духом, мы бы поддались и заменили его 1+2+3+…→-1/12, и получили бы правильный ответ, пропустив почти всю математику в этой статье. Но мы здесь не для этого, мы здесь для того, чтобы выдавить 24 без использования колдовства. Поэтому давайте продолжим.

Почему расходящаяся сумма вообще появилась в этом показателе? Если вы проследите наши расчеты назад, то увидите, как оно вылазит из нулевых энергий КГО — $ E_0 = \frac{\omega}{2} $. Однако энергии нулевого уровня произвольны, и это был просто полезный традиционный выбор. В конечном счете, существует двусмысленность в построении квантового ГО из классического ГО, называемая упорядочивающей двусмысленностью, поскольку вам нужно преобразовать коммутирующие переменные p, q в некоммутирующие операторы $\hat p, \hat q$, и нет никакого предпочтительного «квантования» таких вещей, как pq. Нужно квантование $\hat p, \hat q$? Или $\hat p, \hat q$? Разницей будет константа — произвол в энергии нулевой точки. Таким образом, наш самый консервативный заклад заключается в том, что нулевые колебания здесь фактически суммируются до конечного, но неизвестного значения:

$ Z_{1,L}^{-1} = e^{-irt} \; \prod_k 1 - e^{ikt} $

где r — неизвестное вещественное число. Обратите внимание, что безумный расчет дал бы магическое значение r = 1/24. Итак, потребуется парочка трюков:


  • Я собираюсь показать, используя симметрию, что 1 / r — это число поперечных измерений.
  • Я собираюсь показать, используя другую симметрию, что r = 1/24 в любом случае, даже без 1+2+3+…=-1/12

Чтобы начать говорить об этих симметриях, мне нужно связать мою переменную t с формой тора. Связь заключается в том, что тор строится путем склеивания одноцветных ребер в этом параллелограмме:

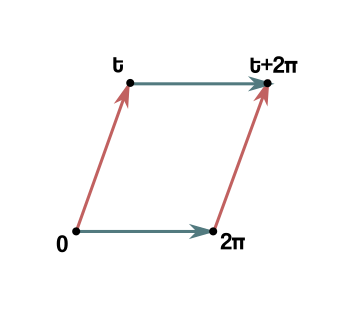
8kaog9365-gtzegspz428ell0ye.png

где t представляется в виде точки на комплексной плоскости. (Сторону 2π выбрали чтоб частоты ω=1,2,3,… были целыми числами). Или для чистоты нотации примем τ=t/2π (+ простое масштабирование, которое, я напоминаю, является симметрией):

ncaxybqm96vjkwdy4-lzr2cblhm.png

Заметим, что при приближении τ к вещественной оси тор вырождается. Это имеет физический смысл: может ли струна действительно замкнуться в себе в реальном времени? Это было бы путешествие во времени. Такое может произойти только во мнимом времени (по крайней мере, в верхней полуплоскости).

При определении $q:=e^{i2\pi\tau}$, наша $Z_{1, L}$ становится

$ Z_{1,L}^{-1}(\tau) = q^r \; \prod_k (1-q^k) $


Трюк первый

Прежде всего, если мы сдвинем τ→τ+1, то получим разные параллелограммы

2ki32vt7rsfak8xrs0cg0minwri.png

но они образуют один и тот же тор после склеивания (проверьте это!). Если форма на самом деле не меняется, то и физические величины не должны меняться.

Однако при этом преобразовании наша амплитуда действительно преобразуется:

$ Z_{1,L}^{-1} \rightarrow e^{2\pi i r} \, Z_{1,L}^{-1} $

Это не имеет смысла… пока мы не вспомним, что это все только для одного измерения. Для поперечных размеров D−2 полная амплитуда равна $Z^{D-2}_{1, L}$, и она останется инвариантной, если

$ r(D-2) = 1 $

это уравнение определяет критическое измерение теории струн. Если мы найдем целое значение 1 / r, то теория будет иметь смысл только в D = 1/r+2 пространственно-временных измерениях.

Теперь доказать, что r = 1/24, будет не так просто. Чтож, попробуем.


Второй трюк

Другая симметрия, которую мы будем рассматривать, — это τ → -1/τ. Полученные торы не идентичны, но они похожи — это масштабированные версии друг друга. Вы можете проверить, что исходная сторона 1 совпадает с новой стороной -1 / τ, а исходная сторона τ совпадает с новой стороной 1. Как мы уже говорили, масштабирование мирового пласта должно быть симметрией.

Таким образом, полная амплитуда должна быть инвариантной; однако мы не должны ожидать этого от $Z^{D-2}_{1, L}$. А? Разве $Z^{D-2}_{1, L}$ не является полной амплитудой? Нет, я солгал, чтобы защитить вас от суровой правды. Истина (часть ее) состоит в том, что колебания на струне всегда происходят парами. Существует множество возможных характеристик этой дихотомии: левые и правые движущие силы, голоморфные и антиголоморфные, синус и косинус…

Важно то, что для нашего $Z_{1, L}$ (L теперь понимается как «левый») также будет парный $Z_{1, R}$ для сестринских колебаний. К счастью, я просто махну рукой, что $Z_{1, R} = Z_{1, L}^*$ так, чтобы общая амплитуда была произведением $|Z^{D-2}_{1, L}|^2$.

Однако это еще не все: хотя мы и учитывали колебания струны относительно «опорного» положения, нам также необходимо учитывать общее движение центра масс в пространстве. Мы хотим, чтобы струна вернулась в исходную точку через время τ, если мы хотим, чтобы она замкнулась в тор;, но мы не можем просто хотеть этого, нам нужно включить амплитуду вероятности, чтобы это заработало.

Какова амплитуда вероятности того, что квантовая частица в 1D останется в одном и том же месте через определенное время? Намек состоит в том, что для чисто мнимых времен уравнение Шредингера является уравнением теплопроводности. И бесконечно концентрированное пятнышко тепла эволюционирует в соответствии с уравнением теплопроводности в 1D, распространяясь в гауссовский пик, пик которого уменьшается как $(time)^{-1/2}$. Таким образом, позвольте мне предположить, что амплитуда для центра масс примерно такова

$ (\Im \tau)^{-1/2} $

Если это так, то, общая амплитуда должна быть примерно такой

$ Z \sim (\Im \tau)^{-\frac{D-2}{2}} \, | Z_{1,L} |^{2(D-2)} $

и для τ→−1/τ:

$ \Im \tau \rightarrow \frac{1}{ | \tau |^2} \Im \tau $

поэтому, если бы $Z_{1, L}$ была трансформирована как-то так

$ Z_{1,L} \rightarrow \tau^{-1/2} Z_{1,L} $

наша общая амплитуда была бы инвариантной, и тогда теория имела бы смысл. Теперь я собираюсь доказать, что это может произойти только в том случае, если r=1/24.


Колдовство

Давайте сделаем некоторые предварительные переобозначения

$ Z_{1,L}^{-1} (\tau) = q^r P(\tau)\,,\quad P(\tau) := \prod_{\ell=1}^\infty (1-q^\ell) $

Тогда, наиболее удобным вариантом представления произведения P (τ) будет:

$-\log P(\tau) = - \sum_{\ell=1}^\infty \log(1-q^\ell) = \sum_{l,k = 1}^\infty \frac{1}{k} q^{k\ell} = \sum_{k = 1} \frac{1}{k} \frac{q^k}{1-q^k} = \sum_{k=1} \frac{1}{k} \frac{1}{q^{-k} -1} $

Я использовал разложение Тейлора для -log (1-x) и геометрический ряд. Если вы не уверены, вы можете более тщательно проверить, разумны ли эти шаги (включая своп суммы) для Im τ>0.

Следующий психоделический аргумент принадлежит Зигелю (да, именно Зигелю). Мы начинаем без видимой причины вот с такой функции комплексной переменной w, с τ в качестве параметра:

$ f(w) = \cot w \cot \frac{w}{\tau} $

а затем, вводя еще один реальный параметр $\nu$ (наш завершающий ход будет заключаться в том, чтобы устремить его в бесконечность), мы строим комбинацию

$ g(w) = \frac{f(\nu w)}{w} $

Давайте посчитаем полюса g. Быстрый осмотр показывает, что существует набор простых полюсов при w=±nkv и еще один при w=±nktv, для k=1,2,3,…; плюс тройной полюс при w=0. Вычеты легко вычисляются следующим образом:

$ \operatorname{Res}_{\pm\frac{\pi k}{\nu}} g = \frac{1}{\pi k}\cot \left( \frac{\pi k}{\tau} \right)\\ \operatorname{Res}_{\pm\frac{\pi k \tau}{\nu}} g = \frac{1}{\pi k}\cot \left( \pi k \tau \right)\\ \operatorname{Res}_{0} g = - \frac{1}{3} (\tau + \tau^{-1}) $

Если вычет в тройной точке (полюс третьего порядка) не кажется очевидным, вспомним, что разложение Тейлора котангенса в нуле начинается $\cot s \sim \frac 1 s - \frac s 3$.

77okvbl1vy6_ii4kti-4ilfpdmu.png
График g (w), для (τ = i), (ν = 1). Белые пятнышки — это полюса, и порядок таков, сколько раз цвета повторяются вокруг них.

Теперь должно быть ясно, что g нам для применения теоремы вычетов. Рассмотрим траекторию γ бегущую против часовой стрелки вокруг параллелограмма с вершинами 1, τ, −1, −τ.

Теорема вычетов гласит:

$ \frac{1}{2\pi i} \int_\gamma \frac{f(\nu w)}{w} d\omega = \sum_{p \in \operatorname{poles}} \operatorname{Res}_p g $

Сумма на самом деле пробегает по полюсам, которые находятся внутри параллелограмма, но мы скоро увидим, что это не то, о чем нам следует беспокоиться.

Теперь я хотел бы использовать это уравнение, чтобы доказать тождество, которое нам действительно нужно. Однако я докажу это только для τ на мнимой оси, потому что это проще, но на самом деле это будет верно для всех Im τ>0. Поскольку обе части уравнения, которое я выведу, голоморфны в τ над верхней полуплоскостью, их согласия на прямой достаточно, чтобы доказать, что они всегда равны. Короче говоря, предположим, что τ пока чисто мнимое, но в конце мы можем просто отбросить это предположение.

Заделаем же интеграл на параллелограмме, который теперь ромб. Для $g(w)=f(\nu w)w^{−1}$, кажется, первообразную сходу не отгадаешь. Итак, возьмем предел ν→∞. Нетрудно заметить, что f (vw) сходится к константе (1,-1,1,-1) соответственно на четырех отрезках γ (если вы ее не видите, запишите ее с помощью комплексных экспонент). Таким образом, в пределе интеграл равен

$ \left( \int_1^\tau - \int_\tau^{-1} + \int_{-1}^{-\tau} - \int_{-\tau}^{1} \right) \frac{dw}{w} $

Легкотня! Интеграл от 1/w — это log w, так что позвольте мне просто приписать его и… ААА! Контур обхода! Нам нужно выбрать обход для логарифма и убедиться, что он не перепрыгивает через берег разреза. Мы можем использовать симметрию чтоб переписать

$ 2\left( \int_1^\tau + \int_1^{-\tau} \right) \frac{dw}{w} $

и теперь, когда весь путь находится справа, мы можем использовать отрицательную действительную ось в качестве берега разреза и, таким образом, использовать главную ветвь логарифма. Просматривая весь путь, получаем

$ 4 \log \left(\frac{\tau}{i} \right) $

Славненько. Теперь о вычетах. Если ν→∞, то все полюса сжимаются и приближаются к началу координат; таким образом, в пределе все они находятся внутри ромба, а сумма идет по всем полюсам. Таким образом, сумма равна

$ -\frac{1}{3} (\tau + \tau^{-1}) + 2 \sum_{k=1}^\infty \left( \frac{1}{\pi k} \cot(\frac{\pi k}{\tau}) + \frac{1}{\pi k} \cot(\pi k \tau) \right) $

на случай, если кто не помнит

$ \cot s = \frac{ e^{is} + e^{-is} }{e^{is} - e^{-is} } = \frac{1 + e^{-2is}}{1 - e^{-2is}} = -1 + \frac{2}{1-e^{-2is}} $

и наша сумма вычетов:

$ -\frac{1}{3} (\tau + \tau^{-1}) + \frac{4}\pi \sum_{k=1}^\infty \frac{1}{k} \left( \frac{1}{1-e^{-\frac{2\pi i k}{\tau}} } - \frac{1}{ 1- e^{-2 \pi i k \tau} } \right) \\ =-\frac{1}{3} (\tau + \tau^{-1}) + \frac{2}{\pi} \left(\log P(-1/\tau) - \log P(\tau) \right) $

Наконец-то мы возвращаемся на Землю. Это начинает выглядеть как теорема о нашем произведении P (τ). Теперь, когда у нас есть обе части равенства, давайте воспользуемся теоремой вычетов.

$ \frac{1}{2} \log\left(\frac{\tau}{i} \right) = - \frac{\pi i}{12} (\tau + \tau^{-1}) - \left(\log P(\tau) - \log(P(-1/\tau) \right) $

А вот и наше магическое число! По крайней мере, половина. Это все еще выглядит как тарабарщина, хотя… давайте для пущей наглядности перейдем к экспонентам:

$ e^{\frac{2\pi i / \tau}{24}} P(-1/\tau) = \sqrt{\tau/i} \; e^{\frac{2 \pi i \tau}{24}} P(\tau) $

Казалось бы, ничего особенного, но комбинация

$ \eta(\tau) := e^{\frac{2\pi i \tau}{24}} P(\tau) = q^{\frac{1}{24}} \prod_{k=1}^\infty (1-q^k) $

как мы недавно доказали, красиво трансформируется при преобразовании τ→-1/τ:

$ \eta(-1/\tau) = \sqrt{\frac{\tau}{i}} \eta(\tau) $

И это все! Именно это мы и искали! Чтоб преобразовать $Z^{-1}_{1, L}(\tau)$ во что надо, замечаем, что оно должно быть самим η (τ), и поэтому r=1/24, и поэтому, наконец

$ D = 26 $


Выводы

Из-за философии, лежащей в основе всего этого поста, чтобы использовать математику как можно более элементарно и чтобы она была самодостаточной, мы ускорили то, что на самом деле является невероятно увлекательной (и, конечно же, гораздо более элегантной) математикой. η (τ) — это, конечно, функция Дедекинда, и мы доказали ее свойства преобразования в модулярной группе; точнее, что модулярный дискриминант $\Delta(\tau):=(2\pi)^{12}\eta^{24}$ является модулярной формой веса 12. Теория струн тесно связана с этой областью математики; на самом деле я надеюсь, что для тех, кто уже знает этот материал, это послужило беглым взглядом на то, что струны даже имеют отношение к модульным формам. В любом случае, я не думаю, что могу судить предмет, который я на самом деле едва знаю по-верхам, так что тут попримолкну.

Иногда всплывает интересный вопрос: если это так неправильно, то почему 1+2+3+…=-1/12, или ζ-регуляризация / тепловое ядро / суммирование Абеля или как бы вы это ни называли, дают малой кровью тот же правильный результат, что и более строгие пути?

У меня нет ни малейшего представления, почему оно так выходит.

Инстинктивно я бы пробормотал что-нибудь о «физическом резоне» или «аналитичности», но, честно говоря, это просто чистое безумие. Это определенно не совпадение, потому что тот же трюк работает и для суперструн. На самом деле я даже не уверен, какова точная взаимосвязь между тремя различными классами доказательств, они выглядят как совершенно разные рассуждения. В квантовании светового конуса при первом чтении вы даже не понимаете, как масштабная / конформная инвариантность вписывается — она очень глубоко зарыта. И если вы случайно знаете какую-то конформную теорию поля, посмотрите, как это доказательство строит 24. Они звучат совсем не как переводы одного и того же, хотя должны.

Удивительно, как много информации о содержании теории несут доказательства D=26 (или D=10), и как много вы уже узнаете о струнах, просто пытаясь объяснить то, что по существу является самым основным фактом теории. Это наглядный пример того, что в теории струн все сходится, ничего не бросается туда просто так, все существенно.


Дополнение

Возможно, существует более быстрое доказательство, если принять теорему Эйлера о пятиугольных числах

$ P(\tau) = \prod_{k=1}^\infty (1-q^n) = \sum_{k=-\infty}^{\infty} (-1)^k q^{k(3k-1)/2} $

Если вы выделите квадрат в экспоненте вы можете переписать

$ P(\tau) = q^{-1/24} \sum_{k=-\infty}^{\infty} (-1)^k q^{\frac{3}{2}(k-\frac{1}{6})^2} $

таким образом

$ \eta(\tau) = q^{1/24} P(\tau) = \sum_{k=-\infty}^{\infty} (-1)^k q^{\frac{3}{2}(k-\frac{1}{6})^2} $

С η в таком виде уже реально доказать $\eta(−1/\tau)=\sqrt{\tau/i}\eta(\tau)$ используя суммирование Пуассона.

Тем не менее, обращение к теореме Эйлера определенно похоже на мошенничество, поэтому я не пошел по этому пути.

© Habrahabr.ru