[Перевод] Произведения и копроизведения30.11.2015 12:03

Это пятая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре в переводе Monnoroch:
0. Теория категорий для программистов: предисловие
1. Категория: суть композиции
2. Типы и функции
3. Категории, большие и малые
4. Категории Клейсли

На КДПВ поросенок Петр заводит по одному трактору в каждый объект категории.

Следуй по стрелкам

Древнегреческий драматург Еврипид писал «Всякий человек подобен своему окружению». Это верно и для теории категорий. Выделить определенный объект категории можно только путем описания характера его взаимоотношений с другими объектами (и самим собой), где отношения — это морфизмы.

Для определения объектов в терминах их взаимоотношений теория категорий прибегает к т. н. универсальным конструкциям. Для этого можно выбрать некоторый шаблон, диаграмму из объектов и морфизмов определенной формы, и рассмотреть все подходящие под него конструкции рассматриваемой категории. Если шаблон достаточно распространен и категория достаточно велика, то, вероятно, найденных конструкций будет очень и очень много. Идея универсальной конструкции состоит в том, чтобы упорядочить конструкции по какому-то закону и выбрать наиболее подходящую.

Этот процесс можно сравнить с поиском в сети. Запрос пользователя — это наш шаблон. Если запрос не очень специфичен, то в ответ поисковая система выдаст множество подходящих документов, только часть из которых релевантны. Чтобы исключить нерелевантные ответы, пользователь уточняет запрос, что увеличивает точность поиска. В конце концов поисковая система проранжирует совпадения и, если повезет, искомый результат будет в самом начале списка.

Начальный (инициальный) объект

Простейший шаблон состоит из одного-единственного объекта. Очевидно, под него подходит каждый объект категории, а их очень и очень много. Чтобы выбрать самый подходящий, нужно ввести на них иерархию. Единственное, что есть в нашем распоряжении, — это морфизмы. Если представлять себе морфизмы как стрелки, то может оказаться, что от одного конца категории до другого простирается всеобъемлющая цепочка стрелок. Это верно в упорядоченных категориях, например, в частичных порядках. Будем говорить, что объект a предшествует объекту b, если существует стрелка (морфизм) из a в b. Было бы естественно называть начальным объект, который предшествует всем прочим (т. е. из него есть стрелка в любой другой объект категории). Ясно, что, вообще говоря, начального объекта может и не быть. Однако намного хуже то, что объектов, удовлетворяющих предыдущему определению, может быть больше одного. Как уточнить наше определение? Подсказку дают упорядоченные категории: в них между двумя объектами существует не более одной стрелки (есть всего один способ быть больше или меньше, чем другой объект). Это приводит нас к следующему определению:

Начальный объект — это объект, из которого в любой объект категории исходит ровно один морфизм.

На самом деле, даже такое определение не гарантирует единственность начального объекта (если он существует). Однако оно гарантирует единственность с точность до изоморфизма. Изоморфизм — очень важное понятие для теории категорий, мы вскоре к нему вернемся.

Рассмотрим несколько примеров. Начальный объект в частично упорядоченном множестве — это его наименьший элемент. Некоторые частично упорядоченные множества, такие как все целые числа (и положительные, и отрицательные), не имеют начального объекта.

В категории множеств начальный объект — это пустое множество. Напомним, пустое множество соответствует типу Void в Haskell (в C++ соответствующего типа нет) и единственной полиморфной функции из Void в любой другой тип, называемой absurd:

absurd :: Void -> a

Существование такой функции и делает Void инициальным объектом категории множеств.

Терминальный объект

Продолжим эксперименты с шаблоном из единственного объекта, но изменим метод ранжирования. Будем говорить, что объект a следует за объектом b, если существует морфизм из b в a (обратите внимание на смену направления). Нас интересует самый последний объект категории. Из соображений единственности определим его так:

Терминальный объект — это объект, в который из любого объекта категории приходит ровно один морфизм.

Опять же терминальный объект единственен с точностью до изоморфизма, что будет вскоре доказано. Однако сперва рассмотрим несколько примеров. В частично упорядоченном множестве терминальный объект (если он существует) является наибольшим объектом. В категории множеств терминальный объект — это синглтон. Напомним, синглтон соответствует типу void в C++ и типу () в Haskell и является типом, населенным ровно одним значением, неявным в C++ и явным в Haskell, обозначаемым как тем же литералом (). Ранее было установлено, что существует единственная чистая функция из любого типа в ():

unit :: a -> ()
unit _ = ()

так что все требования к терминальному объекту выполнены.

Заметим, что в данном случае условие единственности критически важно, поскольку существуют и другие множества (на самом деле, все множества кроме пустого), которые имеют входящие морфизмы из любого другого типа. Например, существует функция со значениями типа Bool (предикат), определенная для любого типа аргумента:

yes :: a -> Bool
yes _ = True

Однако Bool не является терминальным объектом, потому что существует по крайней мере еще одна функция из любого типа в Bool:

no :: a -> Bool
no _ = False

Требование единственности морфизмов дает нам необходимую точность, сужая набор подходящих терминальных объектов до одного.

Двойственность

Нельзя не заметить симметрию между определениями начального и терминального объектов. Вся разница заключается в направлении морфизмов. Для любой категории C можно определить двойственную категорию Cop просто обратив все стрелки вспять. Двойственная категория автоматически удовлетворяет определению категории, если мы одновременно с обращением стрелок переопределим композицию. Если композицией исходных морфизмов f::a->b и g::b->c был h::a->c с h=g∘f, то композицией обращенных морфизмов f_op::b->a и g_op::c->b будет h_op::c->a с h_op=f_op∘g_op. Отметим, что обращение тождественной стрелки совпадает с ней самой.

Двойственность — это очень важное свойство категорий, удваивающее производительность труда теоретико-категорика. Для любой конструкции имеет место двойственная и, доказав одну теорему, вы получаете вторую бесплатно. Конструкции двойственной категории часто имеют префикс «ко»: произведения и копроизведения, монады и комонады, конусы и коконусы, пределы и копределы и т. п. Однако не имеет смысла рассматривать ко-ко-конструкции, ведь дважды обращенная стрелка совпадает с исходной, так что, например, кокомонады совпадают с монадами.

Итак, терминальный объект — это начальный объект в двойственной категории.

Изоморфизмы

Программисты хорошо знают, что определить равенство не так уж и просто. Что означает, что два объекта равны? Должны ли они занимать одну и ту же область памяти (равенство указателей)? Или достаточно того, что значения всех их компонент совпадают? Считаются ли равными два комплексных числа, если одно из них задано действительной и мнимой компонентами, а другое — аргументом и модулем? Можно было бы понадеяться, что математики обладают сакральным знанием об определении равенства, но это не так. В математике также существует множество видов равенства, а также более слабое понятие изоморфизма и еще более слабое — эквивалентности.

Интуитивно объекты изоморфны, если они имеют одинаковый вид, внешне неразличимы: любая часть одного объекта взаимно однозначно соответствует некоторой части другого объекта; по показаниям доступных нам измерительных приборов объекты являются точными копиями друг друга. Математически это означает, что существуют взаимнообратные отображения из объекта a в объект b и из объекта b в объект a. Теория категорий обобщает отображения до морфизмов. Изоморфизм — это обратимый морфизм или, другими словами, пара морфизмов, обратных друг к другу.

Понятие обратимости выражается в терминах композиции и единичного морфизма: морфизм g является обратным к f, если их композиция является единичным морфизмом. На самом деле это не одно, а два условия, поскольку есть два способа композиции пары морфизмов:

f . g = id
g . f = id

Когда мы говорим, что начальный (терминальный) объект единственен с точностью до изоморфизма, то имеется в виду, что любые два начальные (терминальные) объекты изоморфны. Это легко продемонстрировать. Предположим, что i1 и i2 — начальные объекты в одной и той же категории. Поскольку i1 начальный, то существует единственный морфизм f из i1 в i2. Аналогично, поскольку i2 начальный, то существует единственный морфизм g из i2 в i1. Что можно сказать о композиции этих морфизмов?

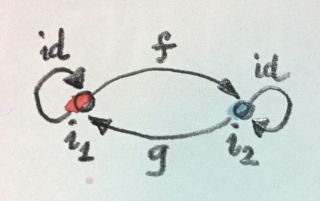
Композиция g∘f должна быть морфизмом из i1 в i1. Но i1 является начальным объектом, так что существует ровно один морфизм из i1 в i1 и, поскольку начало и конец стрелки совпадают, эта вакансия уже занята единичным морфизмом. Следовательно, они должны совпадать: морфизм g∘f является единичным. Аналогично морфизм f∘g также совпадает с единичным, поскольку может быть всего один морфизм из i2 в i2. Таким образом, f и g взаимнообратны, а два начальных объекта изоморфны.

Заметим, что наше доказательство единственности начального объекта с точностью до изоморфизма существенно использовало единственность морфизма из инициального объекта в самого себя. Однако важно ли то, что морфизмы f и g также единственны? Дело в том, что на самом деле мы доказали более строгое утверждение: начальный объект единственен с точностью до единственного изоморфизма. Вообще говоря, между двумя объектами может быть больше одного изоморфизма, но не в этом случае. «Единственность с точностью до единственного изоморфизма» — важное свойство всех универсальных конструкций.

Произведения

Следующая универсальная конструкция — это произведение. Мы уже знакомы с декартовым произведением двух множеств, состоящим из множества всех возможных пар. Какой же шаблон связывает множество-произведение с множествами-множителями? Если мы его выявим, то сможем обобщить понятие произведения на прочие категории.

С декартовым произведением связаны две функции (проекторы), действующие из множества-произведения в соответствующее множество-множитель. В Haskell эти функции называются fst и snd и выбирают первый и второй элементы пары соответственно:

fst :: (a, b) -> a
fst (x, y) = x
snd :: (a, b) -> b
snd (x, y) = y

Здесь функции определены при помощи сопоставления аргумента с образцом: образец соответствует любой паре (x, y) и выделяет ее компоненты в переменные x и y.

Эти определения можно упростить при помощи прочерков:

fst (x, _) = x
snd (_, y) = y

В C++ воспользуемся шаблонным функциями, например:

template
A fst(pair const & p) {
    return p.first;
}

С помощью этой (кажущейся скудной) информации о произведении попробуем сконструировать соответствующий ему шаблон из объектов и морфизмов в категории множеств. Этот шаблон будет состоять из объектов-множителей a и b, объекта c и проецирующих морфизмов p и q:

p :: c -> a
q :: c -> b

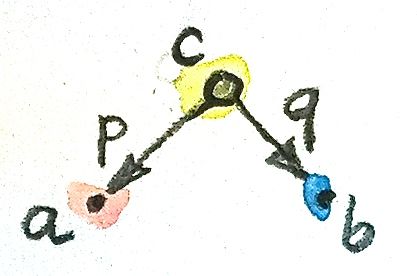
Все объекты c, которые удовлетворяют такому шаблону, будут рассматриваться как кандидаты в произведение. Таких объектов может быть очень много.

Для примера возьмем в качестве множителей два типа, а именно Int и Bool, и рассмотрим выборку кандидатов в их произведение.

Вот первый из них: Int. Может ли Int рассматриваться как кандидат в произведение Int и Bool? Да, может, вот соответствующие проекторы:

p :: Int -> Int
p x = x

q :: Int -> Bool
q _ = True

Выглядит подозрительно, но вполне соответствует шаблону.

Вот еще кандидат: (Int, Int, Bool). Это кортеж из трех элементов. Вот соответствующая пара проецирующих морфизмов (мы снова используем сопоставление с образцом):

p :: (Int, Int, Bool) -> Int
p (x, _, _) = x

q :: (Int, Int, Bool) -> Bool
q (_, _, b) = b

Внимательный читатель мог заметить, что первый кандидат слишком мал — он покрывает только Int-компоненту произведения, а второй слишком велик, потому что включает в себя явно фиктивную Int-компоненту.

Мы пока что рассмотрели только первую составляющую универсальной конструкции — шаблон, но ничего не сказали о второй — о ранжировании. Нам нужен способ, позволяющий сравнить двух кандидатов, соответствующих шаблону, а именно объект c с проекторами p и q и объект c' с проекторами p' и q'. Хотелось бы положить, что c лучше c', если существует морфизм m из c' в c, но это слишком слабое условие. Нужно еще и потребовать, чтобы проекторы p и q были лучше (универсальнее), чем p' и q'. Это означает, что p' и q' могут быть восстановлены по p и q при помощи m:

p’ = p . m
q’ = q . m

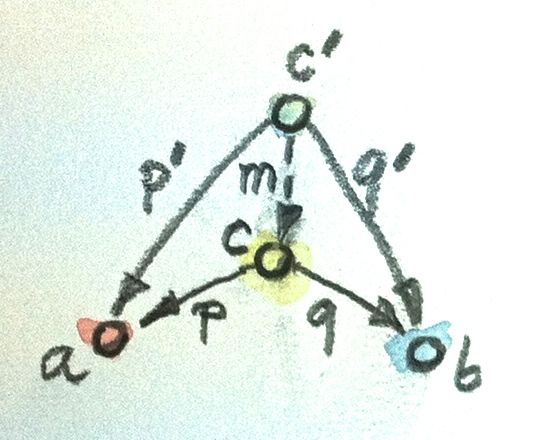
Специалист по теории чисел сказал бы, что m является делителем (фактором) p' и q'. Представьте себе натуральные числа вместо морфизмов и умножение вместо композиции: тогда m окажется общим делителем p' и q'. Далее в подобных ситуациях мы будем говорить, что m факторизует p' и q'.

Для тренировки интуиции покажем, что пара (Int, Bool) с двумя каноническими проекторами fst и snd определенно лучше, чем рассмотренные выше кандидаты.

Отображение m для первого кандидата имеет вид:

m :: Int -> (Int, Bool)
m x = (x, True)

Действительно, оба проектора p и q могут быть восстановлены как:

p x = fst (m x) = x
q x = snd (m x) = True

Морфизм m для второго примера также определен единственным образом:

m (x, _, b) = (x, b)

Мы показали, что (Int, Bool) лучше обоих кандидатов. Покажем, что обратное неверно. Можно ли найти некоторый морфизм m', который позволит восстановить fst и snd по p и q?

fst = p . m’
snd = q . m’

В первом примере q всегда возвращает True, однако в то же время существуют пары, в которых вторым компонентом выступает False. Так что восстановить snd по q нельзя.

Во втором примере дела обстоят иначе: у нас достаточно информации после p и q, чтобы восстановить fst и snd, однако факторизующий морфизм m' определен неоднозначно. Действительно, поскольку и p, и q игнорируют второй элемент кортежа, морфизм m' может поместить туда что угодно:

m’ (x, b) = (x, x, b)

или

m’ (x, b) = (x, 42, b)

и т. д.

Суммируя вышесказанное, для данного типа c с проекторами p и q существует единственный морфизм m из c в декартово произведение (a, b), который факторизует p и q. На самом деле m просто комбинирует их в пару:

m :: c -> (a, b)
m x = (p x, q x)

Это делает декартово произведение (a, b) наилучшим кандидатом и завершает рассмотрение этой универсальной конструкции для категории множеств.

Теперь забудем про множества и определим произведение двух объектов в произвольной категории при помощи той же универсальной конструкции. Такое произведение (если существует) единственно с точностью до единственного изоморфизма.

Произведение объектов a и b — это такой оснащенный двумя проекторами объект c, что для любого другого оснащенного проекторами объекта c' существует единственный морфизм m из c' в c, факторизующий эти проекторы.

Функция (высшего порядка), которая строит факторизующий морфизм по двум проекторам, иногда называется факторизатором. В нашем случае она имеет вид:

factorizer :: (c -> a) -> (c -> b) -> (c -> (a, b))
factorizer p q = \x -> (p x, q x)

Копроизведения

Как и всякая конструкция теории категорий, произведение имеет двойника, называемого копроизведением. Если мы обратим стрелки в шаблоне произведения, то получим объект c, оснащенный двумя вложениями i и j, морфизмами из a и b в c.

i :: a -> c
j :: b -> c

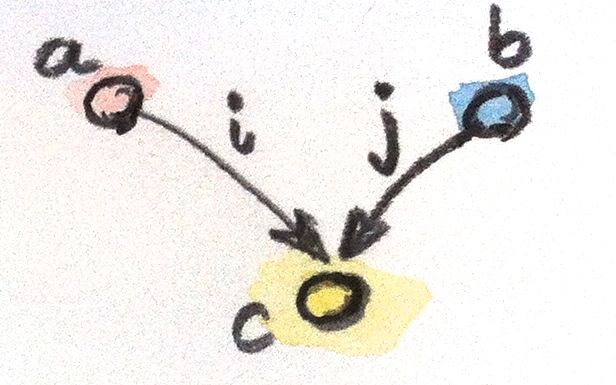
Нам также следует обратить порядок ранжирования: теперь объект c будет считаться лучше объекта c', оснащенного вложениями i' и j', если существует морфизм m из c в c', факторизующий вложения:

i' = m . i
j' = m . j

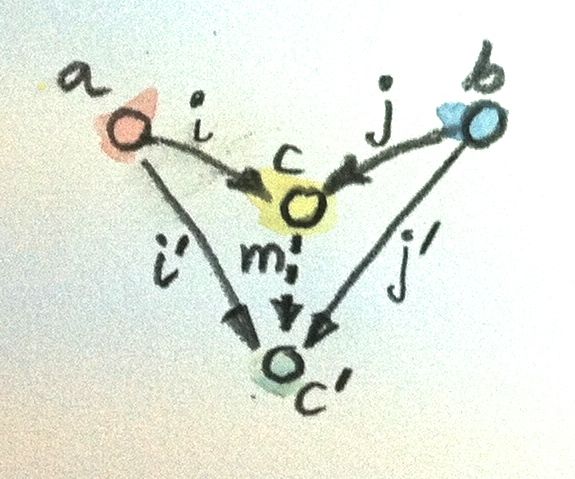
Наилучший из таких объектов, обладающий единственным морфизмом во все прочие отвечающие шаблону объекты, называется копроизведением и, если существует, единственен с точностью до единственного изоморфизма.

Копроизведение объектов a и b — это такой оснащенный двумя вложениями объект c, что для любого другого оснащенного вложениями объекта c' существует единственный морфизм m из c в c', факторизующий эти вложения.

В категории множеств копроизведение — это дизъюнктное объединение. Элемент дизъюнктного объединения a и b — это либо элемент a, либо элемент b. Если два множества пересекаются, то дизъюнктное объединение содержит обе копии общей части. Можно считать, что элементы дизъюнктного объединения помечены метками множеств-источников.

Для программиста копроизведение — это помеченное объединение двух типов. C++ поддерживает непомеченные объединения; задача отслеживания, какой из членов объединения валиден, лежит на плечах программиста. Чтобы создать помеченное объединение нужно определить метку — перечисление — и скомбинировать ее с объединением. Например, помеченное объединение int и char const * может выглядеть так:

struct Contact {
    enum { isPhone, isEmail } tag;
    union { int phoneNum; char const * emailAddr; };
};

Два вложения могут быть реализованы либо как конструкторы, либо как функции. Например, вот первое вложение в виде функции PhoneNum:

Contact PhoneNum(int n) {
    Contact c;
    c.tag = isPhone;
    c.phoneNum = n;
    return c;
}

Эта функция вкладывает int в Contact.

Помеченное объединение также называется variant, обобщенная реализация которого есть в библиотеке boost (boost::variant).

В Haskell можно составить помеченное объединение из любых типов данных, разделяя конструкторы вертикальной чертой. Рассмотренный выше Contact записывается так:

data Contact = PhoneNum Int | EmailAddr String

Здесь PhoneNum и EmailAddr выступают и в качестве конструкторов (вложений), и как метки для сопоставления с образцом (см. ниже). Например, вот так можно построить Contact по телефонному номеру:

helpdesk :: Contact;
helpdesk = PhoneNum 2222222

В отличие от канонической реализации произведения, встроенной в синтаксис Haskell как примитивная пара, каноническая реализация копроизведения является не специальной языковой конструкцией, а рядовым типом данных Either из стандартной библиотеки:

Either a b = Left a | Right b

Этот тип данных параметризован двумя типами a и b и имеет два конструктора: Left, принимающим тип a, и Right, принимающим тип b.

По аналогии с факторизатором для произведения можно определить и факторизатор для копроизведения. Для данного кандидата в копроизведения в виде типа c с двумя вложениями i и j построим факторизующий морфизм:

factorizer :: (a -> c) -> (b -> c) -> Either a b -> c
factorizer i j (Left a)  = i a
factorizer i j (Right b) = j b

Асимметрия

Выше мы рассмотрели две пары двойственных определений: во-первых, определение терминального объекта может быть получено из определения начального объекта обращением стрелок, во-вторых, таким же путем получается определение копроизведения из определения произведения. Однако в категории множеств начальный объект принципиально отличается от терминального, а копроизведение — от произведения. Ниже будет показано, что произведение ведет себя как умножение с терминальным объектом, играющим роль единицы, а копроизведение похоже на сложение, где вместо нуля — начальный объект. В частности, для конечных множеств количество элементов произведения есть произведение количеств элементов в исходных множествах, а количество элементов копроизведения равно сумме исходных количеств.

Это показывает, что категория множеств не является симметричной относительно обращения стрелок.

Заметим, что несмотря на то, что из пустого множества исходит единственная стрелка в любое другое множество (функция absurd), нет ни одного морфизма, входящего в него. Синглтон (множество из одного элемента) имеет не только единственную стрелку, входящую в него из любого множества, но и исходящие стрелки в каждое непустое множество. Как мы видели ранее, эти исходящие из терминального объекта стрелки играют важную роль в выборе элементов других множеств (в пустом множестве нет элементов, так что нечего и выбирать).

Взаимоотношение с синглтоном — это то, чем отличается произведение от копроизведения. Рассмотрим синглтон, состоящий из одного элемента () как объект, отвечающий шаблону произведения. Оснастим его двумя проекторами: пусть p и q — функции из синглтона в каждую из компонент произведения. Обе они выбирают фиксированные элементы в соответствующих множествах. Поскольку произведение является универсальным, то существует (единственный) морфизм m из синглтона в произведение. Этот морфизм выбирает элемент из множества произведения, т. е. фиксированную пару, и факторизует проекторы:

p = fst . m
q = snd . m

Если подставить в эти уравнения единственный элемент синглтона (), то получим:

p () = fst (m ())
q () = snd (m ())

Поскольку m () — это элемент произведения, выбираемый морфизмом m, эти уравнения означают, что элемент p (), выбираемый проектором p из первого множества, является первой компонентой пары, выбираемой m. Аналогично, q () равен второй компоненте. Это полностью согласуется с трактовкой элементов множества-произведения как пар элементов из множеств-множителей.

Однако для копроизведения такой простой интерпретации не существует. Можно попробовать рассмотреть синглтон как кандидата в копроизведения, пытаясь вычленить из него элементы, но в таком случае мы получим два входящих вложения, а не два исходящих проектора. Вложения ничего не говорят о своих источниках (на самом деле, как мы видели ранее, в случае синглтона они с необходимостью игнорируют свой аргумент). То же касается и единственного морфизма из копроизведения в синглтон. Вид на категорию множеств со стороны начального объекта (по стрелкам) совершенно отличен от вида со стороны терминального объекта (против стрелок).

Указанное различие не является специфическим свойством собственно множеств; это свойство функций, который выступают в качестве морфизмов категории множеств Set. Функции по своей природе асимметричны. Рассмотрим этот момент подробнее.

Функция должна быть определена для каждого элемента своей области определения (в программировании такая функция называется тотальной), но не обязана покрывать область значений целиком. Например, функции из синглтона попадают всего в один элемент из области значений. Вырожденным случаем являются функции из пустого множества — они вообще не принимают ни одно из значений. В противоположной ситуации, когда значения функции покрывают все доступные значения, функция называется сюръективной.

Еще одним источником асимметрии является то, что функция может склеить много элементов из области определения в один элемент из области значений. Например, функции в синглтон склеивают все элементы исходного множества в один (). Выше рассматривалась полиморфная функция unit. Если под действием функции образы всех элементов различны, то функция называется инъективной.

Конечно же существуют функции, которые хороши в обоих отношениях, т. е. являются и сюръективными, и инъективными. Они называются биекциями и, поскольку обратимы, образуют симметричную связь между областью определения и областью значений. В категории множеств изоморфизм — это то же самое, что биекция.

Упражнения

Покажите, что терминальный объект единственен с точностью до единственного изоморфизма.
Что представляет собой произведение в частично упорядоченном множестве? Подсказка: воспользуйтесь универсальной конструкцией.
Что представляет собой копроизведение в частично упорядоченном множестве?
Реализуйте аналог Either из Haskell на вашем любимом языке программирования (но не на Haskell).
Покажите, что Either является более подходящим копроизведением, чем int, оснащенный двумя вложениями:
```
int i(int n)  { return n; }
int j(bool b) { return b ? 0 : 1; }
```
Подсказка: определите функцию
```
int m(Either const & e);
```
которая факторизует i и j.
(Продолжение) Аргументируйте, почему int с двумя вложениями i и j не может оказаться предпочтительнее Either?

(Продолжение) Как насчет таких вложений?

int i(int n) {
    if (n < 0) return n;
    return n + 2;
}
int j(bool b) { return b ? 0 : 1; }

Предложите неудачного кандидата в копроизведения для int и bool, который будет хуже Either тем, что допускает несколько морфизмов в Either.

Литература

The Catsters, Products and Coproducts video.

Благодарности

Автор благодарен Гершому Базерману за рецензирование поста перед публикацией и плодотворные дискуссии.