[Перевод] Прогнозируем результаты Чемпионата мира 2022 FIFA простой моделью на Python12.12.2022 17:01

Многие люди (включая меня) называют футбол «непредсказуемой игрой», потому что в футбольном матче есть множество факторов, влияющих на окончательный счёт. И это верно… в определённой степени.

Сложно спрогнозировать окончательный счёт или победителя матча, однако при прогнозировании победителя в соревнованиях всё не так. За последние пять лет «Бавария» выиграла все Бундеслиги, а «Манчестер Сити» выиграл 4 Премьер-лиги.

Совпадение? Не думаю.

На самом деле, в середине сезона 20–21 годов я создал модель для прогнозирования победителя Премьер-лиги, Чемпионата Испании, Чемпионата Италии и Бундеслиги, и она успешно спрогнозировала всех победителей.

Прогноз сделать было не так сложно, потому что на тот момент было сыграно уже 19 матчей. Теперь я запущу ту же модель для прогнозирования результатов Чемпионата мира 2022.
В статье я расскажу, как спрогнозировал победителя Чемпионата мира при помощи Python (подробнее о коде можно узнать из моего часового видеотуториала).

Прим. переводчика: результаты ЧМ показали, что приведённая в этой статье модель допустила довольно много промахов. Однако мы считаем, что она имеет ценность, поэтому публикуем её здесь.

▍ Как мы будем прогнозировать матчи?

Существуют разные способы создания прогнозов. Я могу изготовить сложную модель машинного обучения и передать ей множество переменных, однако прочитав несколько научных статей, я решил дать шанс распределению Пуассона.

Почему? Давайте рассмотрим определение этого распределения.

Распределение Пуассона — это дискретное распределение вероятностей, описывающее количество событий, происходящих в фиксированном временном интервале или области возможностей.

Если мы будем воспринимать гол как событие, которое может произойти за 90 минут футбольного матча, то сможем вычислить вероятность количества голов, которые будут забиты в матче команды А и команды Б.

Но этого недостаточно. Нам ещё нужно соответствовать допущениям распределения Пуассона.

1. Количество событий можно подсчитать (в матче может быть 1, 2, 3 или больше голов).
2. События происходят независимо друг от друга (событие одного гола не должно влиять на вероятность другого).
3. Частота событий постоянна (вероятность того, что гол будет забит в определённый интервал времени, должна быть совершенно одинаковой для любого другого интервала времени той же длины).
4. Два события не могут произойти точно в один момент времени (два гола не могут произойти одновременно).

Допущения 1 и 4 соблюдаются, однако 2 и 3 справедливы лишь частично. Тем не менее, предположим, что допущения 2 и 3 всегда истинны.

Когда я прогнозировал победителей европейских чемпионатов, я создал гистограмму количества голов в каждом матче на протяжении последних пяти лет для четырёх чемпионатов.

Гистограммы количества голов в четырёх чемпионатах

Аппроксимирующая кривая всех чемпионатов похожа на распределение Пуассона.

Мы можем прийти к выводу, что распределение Пуассона подходит для вычисления количества голов, которые могут быть забиты в матче.

Вот формула распределения Пуассона:

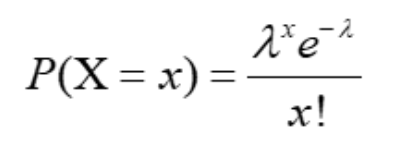
Для создания прогнозов я учёл следующие аспекты:

• lambda: медианное значение голов за 90 минут (команда А и команда Б),
• x: количество голов в матче, которые могли забить команда А и команда Б.

Для вычисления lambda нам нужно среднее количество голов, забитых/пропущенных каждой командой. Это приводит нас к следующему пункту.

▍ Голы забитые/пропущенные каждой командой

Собрав данные со всех матчей Чемпионата мира, сыгранных с 1930 по 2018 год, я смог вычислить среднее количество голов, забитых и пропущенных командой каждой страны.

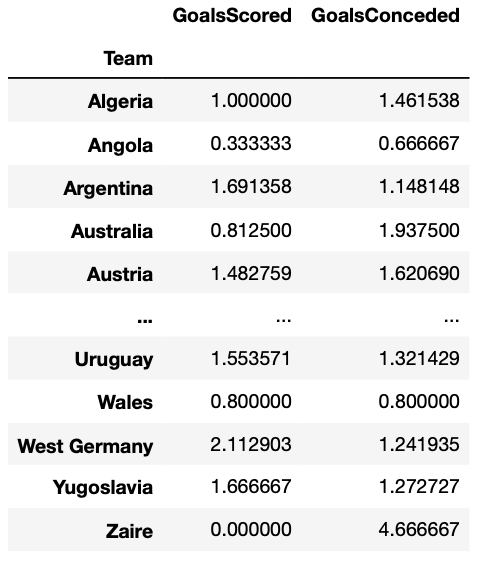
В прогнозе, сделанном для четырёх европейских чемпионатов, я учёл фактор игры дома/в гостях, но поскольку на Чемпионате мира почти все команды играют на нейтральном стадионе, в этом анализе данный фактор не учитывался.

Получив количество голов, забитых/пропущенных командой каждой страны, я создал функцию, предсказывающую количество очков, которые получит каждая команда в групповом этапе.

▍ Прогнозирование группового этапа

Ниже показан код, использованный мной для прогнозирования количества очков, которые получит команда каждой страны в групповом этапе. Выглядит пугающе, однако в этом коде присутствует многое из того, что описано выше.

def predict_points(home, away):
    if home in df_team_strength.index and away in df_team_strength.index:
        lamb_home = df_team_strength.at[home,'GoalsScored'] * df_team_strength.at[away,'GoalsConceded']
        lamb_away = df_team_strength.at[away,'GoalsScored'] * df_team_strength.at[home,'GoalsConceded']
        prob_home, prob_away, prob_draw = 0, 0, 0
        for x in range(0,11): #количество голов команды хозяев
            for y in range(0, 11): #количество голов команды гостей
                p = poisson.pmf(x, lamb_home) * poisson.pmf(y, lamb_away)
                if x == y:
                    prob_draw += p
                elif x > y:
                    prob_home += p
                else:
                    prob_away += p
        
        points_home = 3 * prob_home + prob_draw
        points_away = 3 * prob_away + prob_draw
        return (points_home, points_away)
    else:
        return (0, 0)

Если объяснять простым языком, predict_points вычисляет количество очков, которые получат команды, играющие дома и в гостях. Чтобы получить их, я вычисляю lambda для каждой команды по формуле average_goals_scored * average_goals_conceded.

Затем я симулирую все возможные результаты матча от 0–0 до 10–10 (этот последний счёт является просто пределом моего интервала голов). Получив lambda и x, я использую формулу распределения Пуассона для вычисления p.

prob_home, prob_draw и prob_away накапливают значение p, если, допустим, матч заканчивается со счётом 1–0 (выиграла команда хозяев), 1–1 (ничья) или 0–1 (выиграла команда гостей). Затем по показанной ниже формуле вычисляется результат.

points_home = 3 * prob_home + prob_draw
points_away = 3 * prob_away + prob_draw

Если мы используем predict_points для прогнозирования матча Англии против США, то получим следующее.

>>> predict_points('England', 'United States')
(2.2356147635326007, 0.5922397535606193)

Это значит, что Англия получит 2,23 очка, а США — 0,59. Я получаю десятичные дроби, потому что использую вероятности.

Если мы применим функцию predict_points ко всем матчам в групповом этапе, то получим первое и второе место в каждой группе, а значит, следующие матчи плей-офф.

▍ Прогнозирование плей-оффов

В плей-оффах мне нужно было прогнозировать не очки, а победителя в каждом из матчей. Поэтому я создал новую функцию get_winner на основе функции predict_points.

def get_winner(df_fixture_updated):
    for index, row in df_fixture_updated.iterrows():
        home, away = row['home'], row['away']
        points_home, points_away = predict_points(home, away)
        if points_home > points_away:
            winner = home
        else:
            winner = away
        df_fixture_updated.loc[index, 'winner'] = winner
    return df_fixture_updated

Если points_home больше points_away, то победителем стала команда хозяев, в противном случае — команда гостей.

Благодаря функции get_winner я могу получить результаты предыдущих турнирных таблиц.

▍ Прогнозирование четвертьфинала, полуфинала и финала

Если я снова использую get_winner, то смогу спрогнозировать победителя Чемпионата мира. И вот окончательный результат!

Запустив функцию ещё раз, я выяснил, что победителем будет…

Бразилия!

Вот и всё! Вот так я спрогнозировал результаты Чемпионата мира 2022 года при помощи Python и распределения Пуассона. Полный код выложен на GitHub. Также вы можете изучить мой список на Medium со всеми статьями, относящимися к этому проекту на Python.

© Habrahabr.ru