[Перевод] Повышаем эффективность распределения точек на сфере19.06.2020 12:21

Наложение решётки Фибоначчи (она же золотая спираль или сфера Фибоначчи) на поверхность сферы — чрезвычайно быстрый и эффективный приближенный метод равномерного распределения точек на сфере. Я продемонстрирую, как небольшие изменения, внесённые в каноническую реализацию, могут привести к значительным улучшениям показателей ближайших соседей.

Рисунок 1. Небольшая модификация канонической решётки Фибоначчи может привести к улучшению расстояния упаковки (максимального расстояния между ближайшими соседями) на 8,3%.
Задача равномерного распределения точек на сфере имеет очень долгую историю. Она обладает огромной важностью во многих областях математики, физики, химии и вычислений, в том числе в численном анализе, теории аппроксимации, кристаллографии, морфологии вирусов, электростатике, теории кодирования и компьютерной графике.

К сожалению, она так и не была точно решена, за исключением небольшого количества частных случаев. Следовательно, практически во всех ситуациях мы можем только надеяться найти близкие к оптимальному решения этой задачи.

Из всех этих почти оптимальных решений один из самых простых способов основан на решётке Фибоначчи, или на золотой спирали. Очевидно, изобретатель этого способа вдохновлялся филлотаксисом (который описывает распределение семян в цветке подсолнуха или в сосновой шишке).

Более того, в отличие от большинства других итеративных или рандомизированных способов, например, имитации отжига, спираль Фибоначчи является одним из немногих способов непосредственного построения, работающих для произвольного количества точек $n$ .

Стандартное современное определение решётки Фибоначчи (см. верхний ряд на рисунке 2), равномерно распределяющей $n$ точек внутри единичного квадрата $[0, 1)^2$ , имеет вид:

$t_i = (x_i,y_i) = \left( \frac{i }{\phi} \% 1 , \frac{i}{n}, \right) \quad \textrm{for }\; 0 \leq i < n \tag{1}$

где

$\phi = \frac{1+\sqrt{5}}{2} = \lim_{n \rightarrow \infty} \left( \frac{F_{n+1}}{F_n} \right)$

а оператор $(\cdot) \%1$ обозначает дробную часть аргумента.

(Этот способ очень хорошо работает и для прямоугольников.)

Для создания спирали Фибоначчи (золотой спирали) (см. нижний ряд на рисунке 2) нужно просто наложить это распределение точек на единичном диске при помощи равноплощадного преобразования

$(x,y) \rightarrow (\theta, r) : \quad (2\pi x, \sqrt{y})$

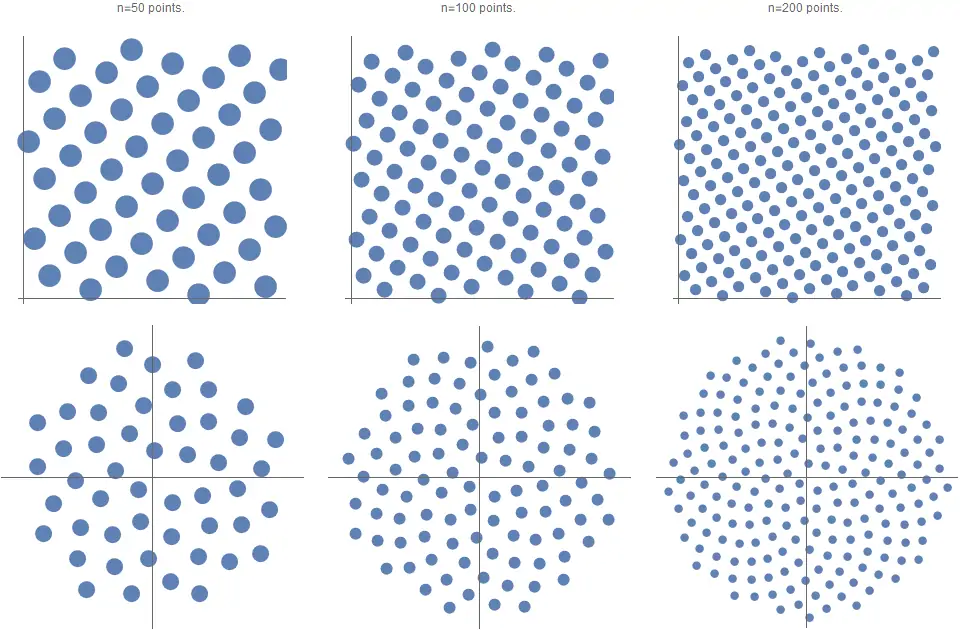
Рисунок 2. Решётка Фибоначчи (верхний ряд) и спираль Фибоначчи (нижний ряд) для различных значений .

Аналогично, эти множества точек можно наложить с единичного квадрата $[0, 1)^2$ на сферу $S^2$ при помощи цилиндрического равноплощадного проецирования (см. рисунок 2):

$(x,y) \rightarrow (\theta, \phi) : \quad \left(2 \pi x, \arccos(1-2y), \right)$

$(\theta,\phi) \rightarrow (x,y,z) : \quad \left (\cos\theta \sin\phi, \sin \theta \sin \phi, \cos \phi \right)$

Стоит заметить, что существует множество стандартов обозначений углов в сферической геометрии. В приведённой выше формуле используется нотация, в которой $\theta \in [0,2\pi]$ является долготой, а $\phi \in [0,\pi]$ — углом от условного севера.

То есть, решётка Фибоначчи — это простой способ очень равномерного распределения точек в прямоугольнике, на диске или поверхности сферы.

(См. примечание 2 о том, почему решётка Фибоначчи не соединяется на всех краях, и почему это хорошо.)

Вот простейшая реализация этого на Python.

from numpy import arange, pi, sin, cos, arccos
n = 50
goldenRatio = (1 + 5**0.5)/2
i = arange(0, n)
theta = 2 *pi * i / goldenRatio
phi = arccos(1 - 2*(i+0.5)/n)
x, y, z = cos(theta) * sin(phi), sin(theta) * sin(phi), cos(phi);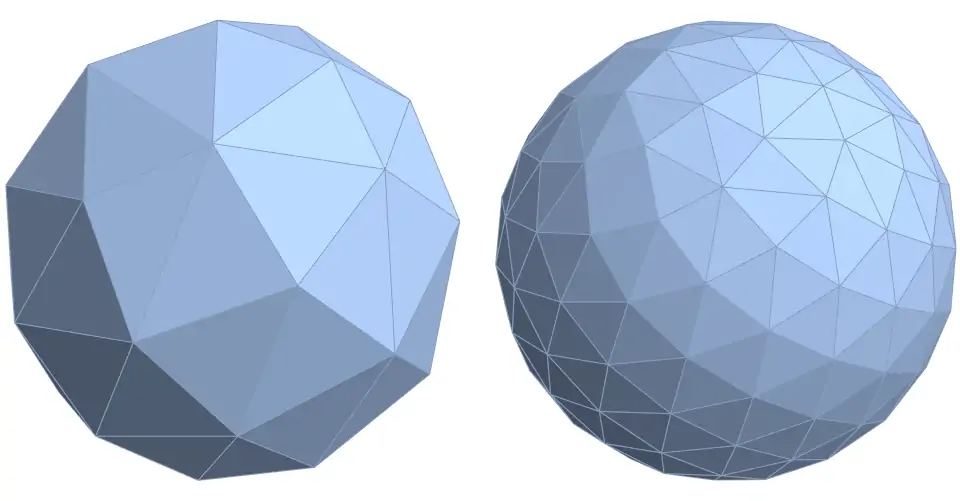

Рисунок 3. Решётка Фибоначчи (или спираль Фибоначчи), наложенная на поверхность сферы — это очень простой способ создания очень равномерного распределения точек.

Эта спираль и наложение на сферу страдают от двух разных, но взаимосвязанных проблем.

Первая заключается в том, что наложение сохраняет площадь, но не расстояние. Если вы стремитесь оптимизировать показатель расстояния, например, между ближайшими соседями, то такие ограничения и отношения расстояний необязательно сохранятся при проецировании площадей.

Вторая проблема, решить которую с практической точки зрения будет сложнее всего, заключается в том, что спиральное наложение имеет расположенную в центре точку сингулярности (а наложение на сферу имеет сингулярность на каждом из полюсов). В случае сферы рассмотрим две точки. находящиеся очень близко к полюсу, но отличающиеся по долготе на 180 градусов. В единичном квадрате (а также в цилиндрической проекции) они будут соответствовать двум точкам, находящимся рядом с верхним краем, но всё равно расположенным достаточно далеко друг от друга. Однако при наложении на поверхность сферы их можно будет соединить очень короткой дугой, проходящей через северный полюс. Именно эта проблема делает многие спиральные наложения неоптимальными. Эта проблема не существует для решётки Фибоначчи в $[0,1)^2$ .

Существует множество одинаково состоятельных критериев для описания степени равномерности распределения точек на поверхности сферы. В том числе:

Упаковка и покрытие
Выпуклые оболочки, ячейки Вороного и треугольники Делоне
Ядра -энергии Риса
Кубатура и определители

Критически важно осознавать, что оптимальное по одному критерию решение часто не является оптимальным распределением точек по другому.

В этом посте мы исследуем только два таких критерия. В основной части рассмотрим самый известный критерий: минимальное расстояние между ближайшими соседями; в оставшейся части мы вкратце опишем среднее расстояние между ближайшими соседями. (См. примечание 3 об исследовании способов оптимизации решётки Фибоначчи под другие критерии).

Задачу поиска максимально ближнего соседа часто называют задачей Тэмса по имени ботаника Тэмса, искавшего объяснение структуры поверхности пыльцевых зёрен. Также её часто называют задачей Фейеша Тота. А конфигурацию, соответствующую таким оптимальным ближайшим соседям, часто называют сферическим кодом.

Платоновы тела

Здесь важно развеять один миф — веру в то, что все платоновы тела (правильные многогранники) являются оптимальными конфигурациями для соответствующих значений $n$ .

К сожалению, это не так. Об этом исчерпывающе написано на сайте Wolfram mathworld:

«В случае двух точек эти точки должны находиться на противоположных концах диаметра. В случае четырёх точек они должны находиться на вершинах вписанного правильного четырёхгранника. Не существует уникального наилучшего решения в случае пяти точек, потому что расстояние невозможно сделать меньше него для шести точек. В случае шести точек они должны быть расположены в вершинах вписанного правильного восьмигранника. В случае семи точек наилучшим решением являются четыре равносторонних сферических треугольника с углами 80 градусов. В случае восьми точек лучшим распределением будут не вершины вписанного куба, а квадратная антипризма с одинаковыми рёбрами многогранника. Решением для девяти точек являются восемь равносторонних сферических треугольников с углами $\arccos(\frac{1}{4})$ . В случае 12 точек решением будет вписанный правильный икосаэдр».

Повторим этот момент, потому что он неочевиден и малоизвестен:

Два платоновых тела — куб ( $n=8$ ) и додекаэдр ( $n=20$ ) не являются оптимальными конфигурациями точек для минимального расстояния между ближайшими соседями. И на самом деле, они далеки от этого.

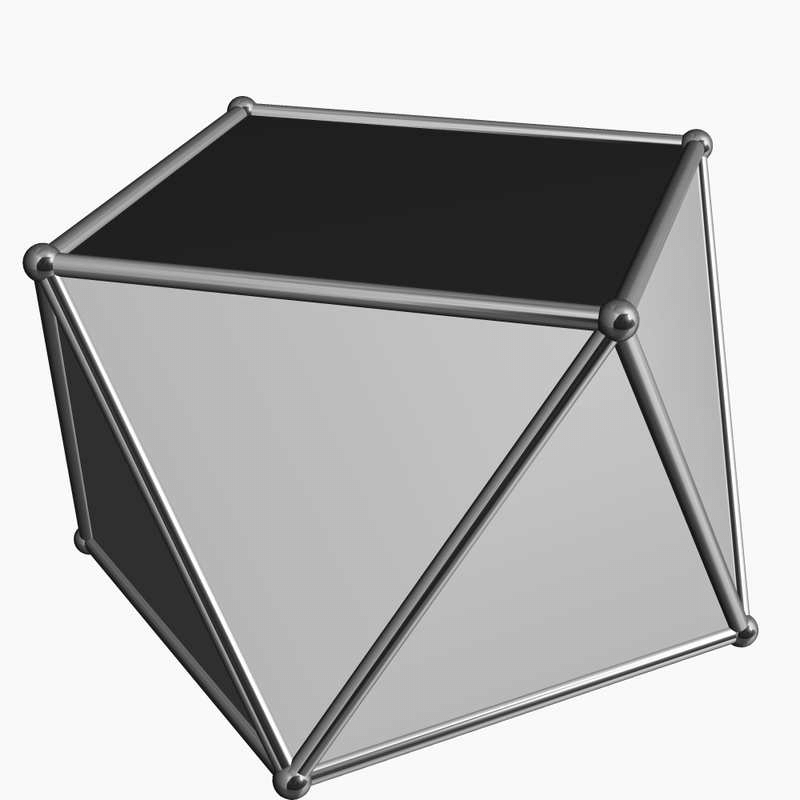
Рисунок 4. Квадратная антипризма («антикуб») является оптимальной конфигурацией упаковки для n=8. (Изображение взято отсюда).

Так что прежде чем мы начнём изучать способы улучшения канонической решётки Фибоначчи для произвольного $n$ , давайте определимся с нотацией.

Пусть для каждой из $n$ точек $\delta_i$ будет расстоянием от точки $i$ до её ближайшего соседа $(0 \leq i < n)$ . Тогда задача Тэмса требует от нас максимизировать минимум $\delta_i$ среди всех $n$ точек. То есть

$\delta_{\rm{min}}(n) = \min_{0\leq i < n} \delta_i$

Это значение уменьшается со скоростью примерно $1/\sqrt{n}$ , то есть полезно также будет задать нормализованное расстояние, а ещё асимптотический предел нормализованного расстояния как

$\delta^*(n) = \sqrt{n} \delta(n) ,\quad \quad \delta^* = \lim_{n \rightarrow \infty} \delta^*(n)$

Каноническая решётка

Стандартная реализация (представленная в приведённом выше коде) разделяет единичный интервал $[0,1)$ на $n$ равных подинтервалов, а затем помещает точку в среднюю точку каждого из этих интервалов (так называемое правило средней точки в интегрировании по Гауссу). То есть

$t_i (\theta, \phi) = \left( \frac{i}{\phi}, \frac{i{+0.5}}{n} \right) \quad \textrm{for }\; 0 \leq i < n \tag{1}$

Этот способ обеспечивает постоянное значение $\delta^*_n=3.09$ для всех $n$ .

Решётка Фибоначчи со смещением

Ключевым моментом для улучшения уравнения 1 является осознание того, что $\delta_\rm{min}(n)$ всегда соответствует расстоянию между точками $t_0$ и $t_3$ , которые расположены рядом с полюсами. То есть для улучшения $\delta(n)$ точки рядом с полюсами должны быть отдалены друг от друга.

Чтобы добиться этого, нам нужно передвинуть (сместить) все точки слегка вдаль от полюсов. Разумеется, это означает, что почти все из них становятся чуть ближе друг к другу. Однако поскольку они не являются критичными для оптимизации $\delta_\rm{min}(n)$ , в такой ситуации это допустимо.

В частности, мы можем достичь этого, задав с каждого конца интервала $(0,1)$ подинтервал длиной $\epsilon$ , где нет точек, а затем равномерно распределив $n$ точек в оставшемся интервале $(\epsilon, 1{-}\epsilon)$ , что гарантирует наличие точки с каждого конца интервала.

То есть

$t_i(\varepsilon) = \left( \frac{i{+ \varepsilon}}{n{-1}{+2\varepsilon}}, \frac{i}{\phi} \right) \quad \textrm{for }\; 0 \leq i < n \tag{2}$

Стоит учесть, что $\varepsilon=\frac{1}{2}$ соответствует канонической решётке, а $$\varepsilon>\frac{1}{2}$» /> представляет увеличившийся зазор рядом с полюсами.</p> <p>Благодаря таким методикам, как Монте-Карло, мы можем эмпирически найти для каждого <img src=$ оптимальное значение $\varepsilon$ , которое оптимизирует расстояние упаковки. Давайте обозначим это оптимальное значение как $\varepsilon^*(n)$ .

Плохая новость заключается в том, что для $\varepsilon^*(n)$ , похоже, не существует простого выражения в конечном виде. Однако хорошая новость заключается в том, что можно найти очень изящные свойства.

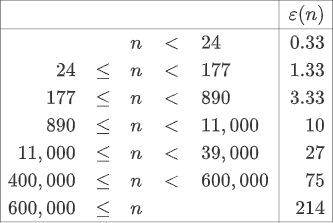
Первое свойство — функция $\varepsilon^*(n)$ является не непрерывной, а ступенчатой функцией, которая (значительно) увеличивается только при определённых значениях $n$ . Более того, соответствующие значения $\varepsilon(n)$ почти всегда очень близки к круглому числу. Если конкретнее, то эмпирический анализ показывает, что превосходным описанием наилучших значений $\varepsilon$ является следующая таблица:

Ниже показана базовая реализация такой решётки со смещением.

from numpy import arange, pi, sin, cos, arccos

n = 50
if n >= 600000:
  epsilon = 214
elif n>= 400000:
  epsilon = 75
elif n>= 11000:
  epsilon = 27
elif n>= 890:
  epsilon = 10
elif n>= 177:
  epsilon = 3.33
elif n>= 24:
  epsilon = 1.33
else:
  epsilon = 0.33

goldenRatio = (1 + 5**0.5)/2
i = arange(0, n) 
theta = 2 *pi * i / goldenRatio
phi = arccos(1 - 2*(i+epsilon)/(n-1+2*epsilon))
x, y, z = cos(theta) * sin(phi), sin(theta) * sin(phi), cos(phi);

При смещении точек решётки Фибоначчи слегка вдаль от полюсов (в соответствии с уравнением 2) создаётся упаковка $\delta^*_{\rm{min}}$ , повышение плотности которой составляет до 8,3%, чем у канонической решётки Фибоначчи.

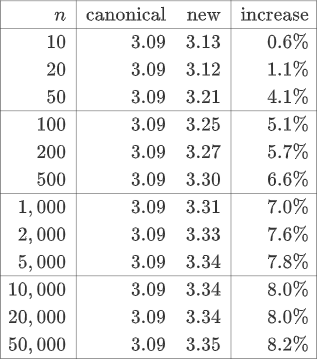
(См. примечание 4 о дополнительных способах изменения канонической решётки, ещё больше увеличивающих $\delta_{\rm{min}}$ .)

Сравнение

Мы можем сравнить этот результат с некоторыми из современных методов, которые обычно являются сложными и требуют рекурсивного и/или динамического программирования (чем выше значение, тем лучше):

Для большого значения $n$ , (а конкретно $n>1000$» />) при оптимизации расстояния упаковки оптимальное значение <img src= довольно велико, что приводит к значительному пробелу или пустоте с каждого полюса.

Простой способ для устранения этого пробела заключается в размещении точки на каждом полюсе с последующим размещением оставшихся $n{-}2$ в соответствии с уравнением 2 и уточнённым смещением $\varepsilon_2$ , представленным в таблице ниже.

Это не только минимизирует пробел на каждом из полюсов, но и обеспечивает небольшое улучшение решётки со смещением, заданной уравнением 2. Величина улучшения очень мала, всего до 1%, и обычно составляет менее 0,1%.

Следовательно, с точки зрения расстояния упаковки она, вероятно, представляет лишь теоретический, а не практический интерес. Однако, в большинстве случаев скорее всего стоит обеспечить её широкую применимость к готовой конфигурации.

Хотя максимизация минимума ближайших соседей является наиболее изученным и чрезвычайно полезным методом с точки зрения теории, она может и не быть наиболее полезным критерием во многих инженерных и вычислительных областях применения.

К сожалению, оптимизация минимального расстояния ближайших соседей обеспечивает неоптимальные конфигурации для среднего расстояния ближайших соседей. Это неудивительно, ведь смещение сдвигает от полюсов все точки, за исключением небольшого количества, а значит, делает их ближе.

Оказывается, что для всех $n$ , по сути, есть одно значение $\varepsilon$ , обеспечивающее наилучшую конфигурацию. А именно $\varepsilon = 0.36$ .

Обратите внимание — поскольку это значение меньше 0.5, точки на самом деле стягиваются ближе к полюсам по сравнению с канонической реализацией!

Хотя при смещении точек с $\varepsilon= 0.36$ создаются неоптимальные конфигурации для расстояний упаковки, в этом случае создаются оптимальные конфигурации по критерию среднего расстояния ближайших соседей. Благодаря этому оно идеально для большинства инженерных и вычислительных областей применения.

Наложение решётки Фибоначчи (золотой спирали, или сферы Фибоначчи) на поверхность сферы — чрезвычайно быстрый и эффективный приближенный способ равномерного распределения точек на сфере.

Однако смещение точек решётки Фибоначчи немного вдаль от полюсов (в соответствии с уравнением 2) приводит к созданию конфигурации точек, упаковка которой повышается максимум на 8,3% по сравнению с канонической решёткой Фибоначчи (по критерию расстояния упаковки).

При $n>100$» /> увеличение может стать ещё больше — сначала нужно разместить по точке на каждом из полюсов, а затем расположить оставшиеся <img src= точек в соответствии с уравнением 2 и смещением по таблице из раздела 4. Это не только (очень незначительно) улучшает упаковку ближайших соседей, но и предотвращает появление большого зазора на каждом из полюсов.

Примечания

1. Строго говоря, сфера состоит только из всех точек, равноудалённых от центра. Именно множество всех таких точек образует поверхность. Следовательно, фраза «поверхность сферы» является тавтологией. Однако в этом посте я часто использую эту фразу, чтобы не запутывать читателей.

2. Оператор $\%1%$ решётки Фибоначчи (см. верхний ряд рисунка 1) обозначает, что мы на самом деле накладываем единичный квадрат на цилиндр. Часто считается, что новое пространство является тором, но при внимательном наблюдении заметно, что точки рядом с верхним и нижним краями выровнены неточно. В нашем случае, когда выполняется наложение решётки на диск или на поверхность сферы, это на самом деле идёт нам на пользу, потому что уменьшает ограничения, а значит, обеспечивает бОльшую степень свободы при поиске хороших разделений точек.

Именно по этой причине наложение решётки Фибоначчи на поверхность сферы практически всегда обеспечивает лучшие результаты, чем наложение на поверхность сферы обычного двухмерного ряда с низким расхождением (в котором все края соединяются).

3. В этом посте исследуются критерии, касающиеся ближайших соседей. Об оптимизации таких конфигураций, при которых максимизируется объём выпуклой оболочки можно прочитать в моём предыдущем посте «Равномерное распределение точек на сфере» [перевод на Хабре].

4. Перемещение точек всё дальше от точек даёт нам понять, что существует определённый предел, при котором конструктивно располагать точки на каждом из полюсов. Подробности этого изложены в моём предыдущем посте об этой теме, ссылку на который я указал в примечании 3. Однако при этих новых найденных оптимальных значениях $\varepsilon$ эта дополнительная сложность повышает $\delta_{\rm{min}}$ всего максимум на 0,2%, поэтому в большинстве областей применения реализовывать её скорее всего не стоит.

[Перевод] Повышаем эффективность распределения точек на сфере19.06.2020 12:21

Примечания

Важные ссылки