[Перевод] Поиск с помощью регулярных выражений может быть простым и быстрым
В этой статье мы рассмотрим два способа поиска с помощью регулярных выражений. Один широко распространён и используется в стандартных интерпретаторах многих языков. Второй мало где применяется, в основном в реализациях awk и grep. Оба подхода сильно различаются по своей производительности:
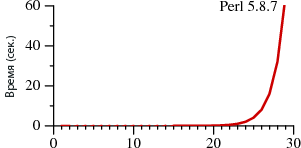
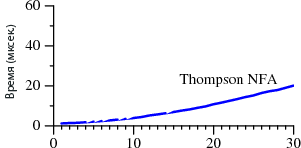
В первом случае поиск занимает A?nAn времени, во втором — An.
Степени обозначают повторяемость строк, то есть A?3A3 — это то же самое, что и A?A?A?AAA. Графики отражают время, требуемое для поиска через регулярные выражения.
Обратите внимание, что в Perl для поиска строки из 29 символов требуется более 60 секунд. А при втором методе — 20 микросекунд. Это не ошибка. При поиске 29-символьной строки Thompson NFA работает примерно в миллион раз быстрее. Если нужно найти 100-символьную строку, то Thompson NFA справится менее чем за 200 микросекунд, а Perl понадобится более 1015 лет. Причём он взят лишь для примера, во многих других языках наблюдается та же картина — в Python, PHP, Ruby и т. д. Ниже мы рассмотрим этот вопрос более детально.
Наверняка вам трудно поверить приведённым данным. Если вы работали с Perl, то вряд ли подмечали за ним низкую производительность при работе с регулярными выражениями. Дело в том, что в большинстве случаев Perl обращается с ними достаточно быстро. Однако, как следует из графика, можно столкнуться с так называемыми патологическими регулярными выражениями, на которых Perl начинает буксовать. В то же время у Thompson NFA такой проблемы нет.
Возникает логичный вопрос: а почему бы в Perl не использовать метод Thompson NFA? Это возможно и следует делать, и об этом пойдёт далее речь.
Раньше регулярные выражения были яркой иллюстрацией того, как использование «хорошей теории» может привести к созданию хороших программ. Изначально они были созданы в качестве простой теоретической вычислительной модели, а затем Кен Томпсон реализовал их в одной из версий текстового редактора QED для CTSS. Деннис Ритчи сделал то же самое в своей собственной версии QED для GE-TSS. Позднее Томпсон и Ритчи приложили руку к созданию UNIX, перенеся туда и регулярные выражения. В конце 1970-х они были одной из главных особенностей этой ОС и использовались в таких инструментах, как ed, sed, grep, egrep, awk и lex.
Сегодня регулярные выражения служат не менее яркой иллюстрацией того, как игнорирование «хорошей теории» приводит к созданию плохих программ. Реализации регулярных выражений во многих современных инструментах работают значительно медленнее тех, что использовались 30 лет назад в UNIX-инструментах.
В этой статье мы рассмотрим разные аспекты «хорошей теории», а также её практическую реализацию алгоритма Томпсона. Она состоит менее чем из 400 строк на языке С и очень близка к той, что используется в Perl, Python, PCRE и ряде других языков.
Так называют способ описания шаблонов строковых данных. Если некий набор строковых данных аналогичен тому, что описывается регулярным выражением (РВ), то мы говорим о совпадении РВ с этими строковыми данными.
Простейшим случаем регулярного выражения является одиночный буквенный символ. За исключением метасимволов — *, +, ?, (, ), и |, — все символы равны сами себе. Для поиска совпадений с метасимволами нужно добавлять обратный слеш: комбинация символов \+ аналогична +.
Два регулярных выражения могут преобразовываться или объединяться, создавая новое регулярное выражение: если E1 соответствует S, а E2 соответствует t, тогда E1|E2 соответствует S или T, а E1E2 соответствует ST.
Метасимволы *, + и? являются операторами цикла:
- E1* говорит о том, что E1 может встречаться 0 и более раз;
- E1+ говорит о том, что E1 может встречаться 1 и более раз;
- E1? говорит о том, что E1 может встречаться 0 или 1 раз.
Приоритетность операторов распределяется по возрастанию степени связывания (binding): сначала операторы чередования (alternation), затем конкатенации (concatenation) и, наконец, операторы повторения (repetition). Круглые скобки могут использоваться для выделения подвыражений, наподобие арифметических: AB|cd соответствует (AB)|(cd), AB* соответствует A(B*).
Описанный синтаксис является подмножеством синтаксиса, используемого в egrep. Этого достаточно для описания всех регулярных языков (regular languages). Грубо говоря, регулярный язык представляет собой набор строк, которые могут быть найдены в тексте за один проход с использованием фиксированного объёма памяти. Современные реализации регулярных выражений (в Perl и ряде других языков) используют многочисленные новые операторы и управляющие последовательности. Это делает РВ более лаконичными, а иногда и довольно непонятными. Но эффективности не прибавляется, поскольку почти все эти новые выражения можно выразить с помощью «традиционного» синтаксиса, просто в более длинной форме.
Дополнительные возможности предоставляют так называемые обратные связи (backreferences). Обратная ссылка \1 или \2 соответствует строке, аналогичной предшествующему выражению, заключённому в круглые скобки. (cat|dog)\1 соответствует catcat и dogdog, а не catdog или dogcat.
С точки зрения теории регулярные выражения с обратными связями уже не являются регулярными выражениями. Использование обратных ссылок имеет свою немалую цену: в разных реализациях приходится использовать экспоненциальные алгоритмы поиска. Конечно, Perl (как и другие языки) нельзя избавить от поддержки обратных связей. Но зато в их отсутствие можно использовать куда более быстрые алгоритмы.
Конечные автоматы можно использовать для описания шаблонов. Они также известны как машины состояний (state machines). В рамках данной статьи понятия «автомат» и «машина» будут взаимозаменяемыми.
Пример распознавания машиной шаблона, соответствующего регулярному выражению A(BB)+A:

Конечный автомат всегда находится в одном из состояний, обозначенных как S0…S4. Когда автомат считывает данные, он переходит в следующее состояние. Есть два особых состояния: S0 — начальное, S4 — состояние совпадения (matching state).
Автомат считывает входящие данные по одному символу за раз, последовательно переходит из одного состояния в другое в зависимости от текущего символа. Возьмём набор ABBBBA. Когда машина считывает первую A, она находится в состоянии S0. Затем переходит в S1. Далее процесс повторяется по мере считывания остальных символов: B — S2, B — S3, B — S2, B — S3 и, наконец, A — S4.
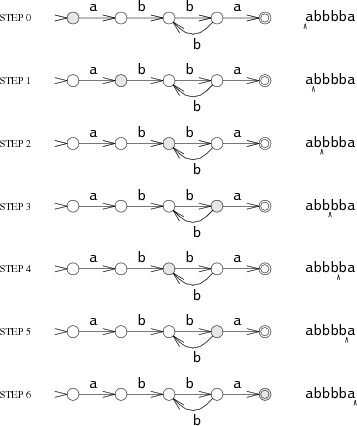
Если машина останавливается в состоянии S4, значит, символ найден; если в другом состоянии — не найден.
Рассмотренный вид машины называется детерминированным конечным автоматом (DFA, deterministic finite automaton), поскольку вне зависимости от текущего состояния каждый новый входной символ приводит к переходу в следующее состояние. Можно создать машину, которая будет выбирать, в какое именно состояние ей перейти.

Эта машина аналогична предыдущей, но не является детерминированной, потому что если B считывается в состоянии S2, то машина может перейти как обратно в S1 (в надежде получить ещё одно BB), так и в S3 (в надежде получить последнюю A). Поскольку машина не знает, какие ещё символы входят в шаблон, то и не может оценить, какое решение будет верным. То есть она всегда угадывает. Подобные машины называются недетерминированными (NFA или NDFA, nondeterministic finite automata). NFA находит совпадение, если может считать символ и перейти в состояние совпадения.
Иногда удобнее позволить NFA менять состояние в любое время без считывания входящих данных. На схеме это обозначено немаркированным переходом (стрелкой без подписей). Например, такой вариант будет самым выигрышным в случае с шаблоном A(BB)+A:
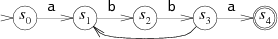
Функционально они абсолютно равнозначны. Каждому регулярному выражению можно сопоставить эквивалентный NFA (они будут искать одинаковые шаблоны), и наоборот. Есть разные способы преобразования регулярных выражений в NFA. Один из них, описанный ниже, был предложен Томпсоном в 1968 году.
NFA для регулярного выражения собирается из частичных NFA для каждого из подвыражений, с разной конструкцией для каждого оператора. Частичный NFA не имеет состояния совпадения, вместо этого он содержит один или несколько «висячих» переходов. Процесс сборки завершается тогда, когда эти переходы приводят к состоянию совпадения.
NFA для поиска одиночных символов выглядят так:
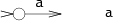
NFA для конкатенации E1E2 состоит из машины E1, чей финальный переход соединяется с началом машины E2:
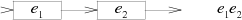
В NFA для чередования E1|E2 добавляется новое начальное состояние с выбором следования через машину E1 или E2:
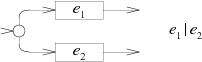
В NFA для E? машина E чередуется с пустым переходом:
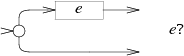
В NFA для E* используется такое же чередование, но машина E зацикливается на начальное состояние:
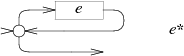
В NFA для E+ также присутствует цикл, но в данном случае нужно хотя бы раз пройти через E:
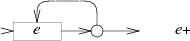
Если проанализировать приведённые выше схемы, то можно заметить, что для каждого символа или метасимвола в регулярном выражении (за исключением круглых скобок) создаётся отдельное состояние. Таким образом, число состояний результирующего NFA как минимум соответствует длине исходного регулярного выражения.
Как и в случае с ранее рассмотренным примером NFA, немаркированные переходы можно либо не использовать с самого начала, либо убрать их уже после сборки. Но их наличие облегчает нам чтение и понимание NFA, так что мы их сохраним и далее.
Теперь у нас есть способ проверить, содержится ли РВ в строке: преобразуем регулярное выражение в NFA и запустим его, используя строку в качестве входных данных. Помните, что NFA могут хорошо угадывать, в какое состояние им перейти. Для использования NFA на обычном компьютере надо выбрать подходящий алгоритм.
Например, можно перебирать варианты, пока не будет найден подходящий. Рассмотрим NFA для ABAB|ABBB, выполняющий поиск по ABBB:
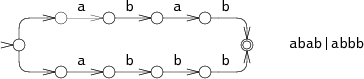
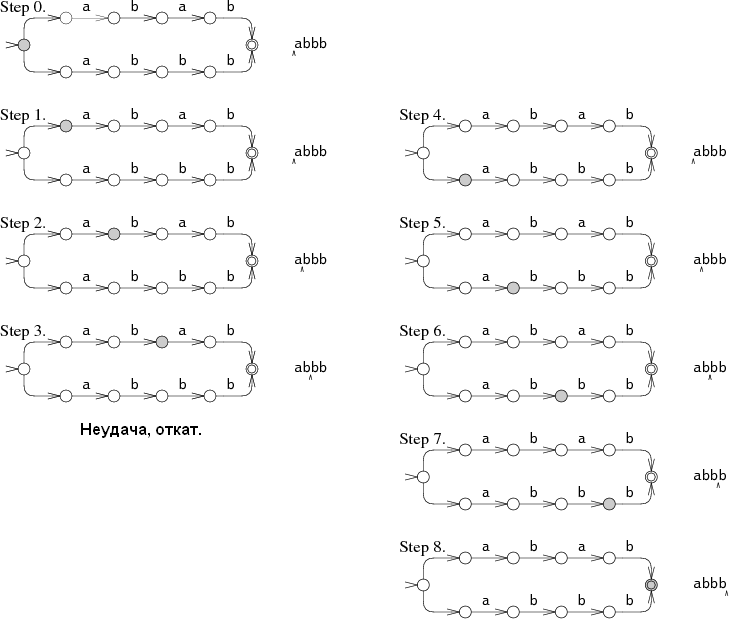
В ходе действия 0 NFA должен решить, искать ему ABAB или ABBB. В нашем примере он выбрал первый вариант и во время действия 3 потерпел неудачу. Затем он пробует искать вторую комбинацию и находит во время действия 4. Данный подход имеет рекурсивную реализацию и позволяет многократно считывать данные для успешного поиска. Машина должна испробовать все возможные варианты, прежде чем прекратить выполнение. В этом примере показаны только две ветки, но в жизни их количество может расти экспоненциально, что очень сильно снижает производительность поиска.
Другой подход сложнее, но более эффективен. Речь идёт об одновременном поиске по обоим шаблонам. В этом случае машина может находиться сразу в нескольких разных состояниях. При обработке каждого символа она проходит через все соответствующие состояния.
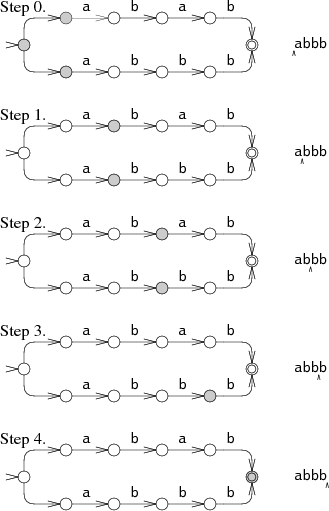
Выполнение машины начинается одновременно с начального состояния и всех других состояний, к которым ведут немаркированные переходы. Во время действий 1 и 2 NFA находится сразу в двух состояниях. При таком подходе данные считываются только один раз, а машина одновременно пытается идти по двум веткам. В самых «запущенных» случаях NFA может во время каждого действия находиться одновременно во всех состояниях. В результате продолжительность поиска получается очень большой вне зависимости от длины шаблона и в течение линейного времени могут обрабатываться шаблоны любого размера. Это своеобразная компенсация за экспоненциальное время работы при использовании бэктрекинга. Эффективность зависит от набора одновременно доступных состояний, а не от путей перехода к ним. Если NFA состоит из N узлов, то во время каждого действия может находиться одновременно максимум в N состояний, а количество переходов может достигать 2N.
Данный подход — когда машина находится одновременно в нескольких состояниях — был предложен Томпсоном в 1968 году. В его интерпретации каждое состояние было описано небольшими кусками машинного кода, а список возможных состояний представлял собой последовательность инструкций по вызову функций. В сущности, Томпсон скомпилировал регулярные выражения в грамотный машинный код. Сегодня, 40 лет спустя, и компьютеры куда мощнее, и машинный код использовать не обязательно. Поэтому ниже представлен вариант реализации на ANSI C. Полный код (менее 400 строк) и скрипты-бенчмарки можно скачать отсюда: http://swtch.com/~rsc/regexp/. Если вы не дружите с языком С, то можете почитать описания.
Начнём с того, что компилируем РВ в эквивалентный NFA. В нашем С-коде NFA представлен в виде связанной коллекции структур State:
struct State
{
int c;
State *out;
State *out1;
int lastlist;
};
Каждая из них соответствует одному из трёх последующих фрагментов NFA:
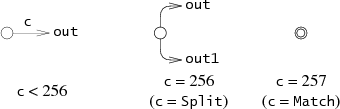
lastlist используется во время выполнения, его роль будет объяснена ниже.
Компилятор создаёт NFA из регулярного выражения в постфиксной нотации с добавлением точки (.) — явного оператора конкатенации. Отдельная функция re2post перезаписывает регулярные инфиксные выражения наподобие A(BB)+A в виде эквивалентных постфиксных выражений ABB.+.A…
В «настоящей» реализации точку нужно использовать в качестве метасимвола «любой символ», а не в качестве оператора конкатенации. Возможно также, что в реальной ситуации NFA придётся компилировать в ходе парсинга, а не создавая явное постфиксное выражение. Но постфиксный вариант удобнее и больше соответствует предложенному Томпсоном подходу.
В ходе сканирования постфиксного выражения компилятор создаёт стек вычисленных NFA-фрагментов. Наличие литеральной константы приводит к добавлению нового фрагмента, а каждый оператор требует сначала удаления фрагмента из стека, а затем добавления нового. Например, после компиляции ABB в ABB.+.A. в стеке появляются NFA-фрагменты для A, B и B. Компиляция точки приводит к удалению двух фрагментов для B и добавлению фрагмента для конкатенации BB… Каждый фрагмент определяется начальным состоянием и исходящими переходами:
struct Frag
{
State *start;
Ptrlist *out;
};
Start обозначает начальное состояние фрагмента, а out — список указателей на указатели State*, которые пока ещё никуда не ведут. В NFA-фрагменте они выглядят как висячие переходы.
Списком указателей можно манипулировать с помощью вспомогательных инструкций:
Ptrlist *list1(State **outp);
Ptrlist *append(Ptrlist *l1, Ptrlist *l2);
void patch(Ptrlist *l, State *s);
List1 создаёт новый список, содержащий единственный указатель outp. Append объединяет два списка и возвращает результат. Patch соединяет висячие переходы в списке l с состоянием s: для каждого указателя outp в списке l устанавливается *outp = s.
На основании этих элементов и стека фрагментов из постфиксного выражения создаётся простой цикл. Напоследок остаётся добавить один фрагмент: изменение состояния завершает NFA.
State*
post2nfa(char *postfix)
{
char *p;
Frag stack[1000], *stackp, e1, e2, e;
State *s;
#define push(s) *stackp++ = s
#define pop() *--stackp
stackp = stack;
for(p=postfix; *p; p++){
switch(*p){
/* compilation cases, described below */
}
}
e = pop();
patch(e.out, matchstate);
return e.start;
}
Этапы компиляции, соответствующие описанным ранее этапам преобразования:
Символьные литералы:
default:
s = state(*p, NULL, NULL);
push(frag(s, list1(&s->out));
break;
Катенация:
case '.':
e2 = pop();
e1 = pop();
patch(e1.out, e2.start);
push(frag(e1.start, e2.out));
break;
Чередование:
case '|':
e2 = pop();
e1 = pop();
s = state(Split, e1.start, e2.start);
push(frag(s, append(e1.out, e2.out)));
break;
Ноль или более:
case '*':
e = pop();
s = state(Split, e.start, NULL);
patch(e.out, s);
push(frag(s, list1(&s->out1)));
break;
Один или более:
case '+':
e = pop();
s = state(Split, e.start, NULL);
patch(e.out, s);
push(frag(e.start, list1(&s->out1)));
break;
После создания NFA нам нужно его смоделировать. Для этого необходимо отслеживать наборы состояний Sets, хранящиеся в виде простого списка массива:
struct List
{
State **s;
int n;
};
При моделировании используются два списка:
- clist — текущий набор состояний, в которых находится NFA;
- nlist — следующий набор состояний, в которые перейдёт NFA после обработки текущего символа.
При начале цикла выполнения в clist заносится лишь начальное состояние и инициализируется работа машины, по одному действию за раз.
int match(State *start, char *s)
{
List *clist, *nlist, *t;
/* l1 and l2 are preallocated globals */
clist = startlist(start, &l1);
nlist = &l2;
for(; *s; s++){
step(clist, *s, nlist);
t = clist; clist = nlist; nlist = t; /* swap clist, nlist */
}
return ismatch(clist);
}
Чтобы не распределять при каждой итерации, match использует в качестве clist и nlist два предраспределённых списка l1 и l2.
Если в списке финальных состояний присутствует состояние совпадения, значит, мы нашли искомый набор символов:
int ismatch(List *l)
{
int i;
for(i=0; i<l->n; i++)
if(l->s[i] == matchstate)
return 1;
return 0;
}
Состояние добавляется в список с помощью addstate, но только если оно в нём пока отсутствует. Сканировать список при каждом добавлении было бы неэффективно, вместо этого переменная listid используется для контроля версии списка. Когда addstate добавляет в список состояние S, значение listid записывается в s->lastlist. Если их значения равны, то, следовательно, S уже присутствует в списке. Если S является состоянием Split, из которого возможны немаркированные переходы к новым состояниям, то addstate добавляет эти состояния в список вместо S.
void
addstate(List *l, State *s)
{
if(s == NULL || s->lastlist == listid)
return;
s->lastlist = listid;
if(s->c == Split){
/* follow unlabeled arrows */
addstate(l, s->out);
addstate(l, s->out1);
return;
}
l->s[l->n++] = s;
}
Список начальных состояний создаётся с помощью startlist:
List* startlist(State *s, List *l)
{
listid++;
l->n = 0;
addstate(l, s);
return l;
}
Наконец, step говорит NFA начать обработку следующего символа, используя текущий clist для создания nlist:
void step(List *clist, int c, List *nlist)
{
int i;
State *s;
listid++;
nlist->n = 0;
for(i=0; i<clist->n; i++){
s = clist->s[i];
if(s->c == c)
addstate(nlist, s->out);
}
}
Описанная выше реализация не может похвастаться высокой производительностью. Но бывает так, что медленная реализация алгоритма линейного времени легко обходит быструю реализацию алгоритма экспоненциального времени, если экспонента достаточно велика. Это хорошо демонстрируется при тестировании различных популярных движков на так называемых патологических регулярных выражениях.
Давайте рассмотрим РВ A?NAN. Если A? позволяет не искать совпадений по каким-либо символам, тогда это РВ будет соответствовать AN. В реализациях РВ с бэктрекингом при поиске 1-или-0? сначала будет искаться 1, а затем 0. Количество подобных выборов может достигать N, а количество возможностей — 2N. И только самая последняя возможность — выбор 0 для всех? — приведёт к совпадению. При использовании метода с бэктрекингом выполнение занимает O(2N) времени, так что при N ≥ 25 степень масштабирования становится невелика.
Для сравнения, при длине набора символов N алгоритм Томпсона тоже подразумевает около N возможных состояний, но выполняет поиск за время O(N2). Поскольку константа РВ не сохраняется при увеличении входных данных, время выполнения описывается сверхлинейной функцией. Если длина РВ равна M, а поиск осуществляется по тексту длиной N, то при использовании алгоритма Томпсона время выполнения составляет O(MN).
Поиск совпадения A?NAN по AN (размер РВ и текста равен N):
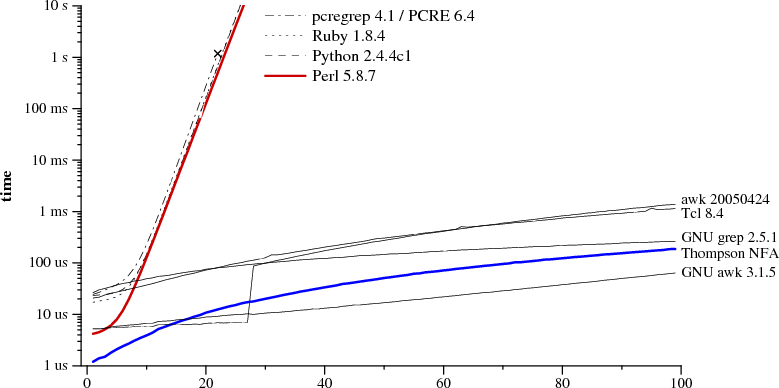
Обратите внимание, что ось Y имеет логарифмическую шкалу. Это сделано для удобства отображения различных реализаций.
Как видите, в Perl, Python, PCRE и Ruby используется рекурсивный бэктрекинг. В PCRE правильный результат нельзя получить уже при N = 23 из-за прерывания бэктрекингов в связи с достижением максимального количества действий. В движке Perl осуществляется мемоизация поиска, что позволяет существенно снизить временные затраты за счёт некоторого увеличения использования памяти, несмотря на использование обратных ссылок. Но, как видно из графика, мемоизация здесь неполная: время выполнения растёт экспоненциально даже в отсутствие обратных ссылок в выражениях. В Java, хоть он и не изображён на графике, тоже используется реализация с бэктрекингом. Интерфейс java.util.regex требует наличия бэктрекингов, поскольку в поисковый путь может подставляться произвольный Java-код. А в PHP используется библиотека от PCRE.
Синей линией на графике изображена производительность алгоритма Томпсона, реализованного в языке С. В awk, Tcl, GNU grep и GNU awk осуществляется сборка и предварительный просчёт DFA на лету, об этом мы поговорим ниже.
Кто-то возразит, что этот тест несправедлив по отношению к реализации с бэктрекингом, поскольку сравнение проводится на примере нестандартной тупиковой ситуации. Но здесь важно другое: когда стоит выбор между методом, имеющим предсказуемое время выполнения (причём небольшое) при всех видах входных данных, и методом, который обычно имеет хорошую производительность, но в ряде случаев может потребовать тысяч машино-часов, то решение должно быть очевидно.
Да, на практике редко возникают ситуации, в которых производительность поиска столь удручающая. Но всё же бывает немало задач, при которых скорость поиска достаточно низка. Например, когда для получения пяти полей, разделенных пробелом, используют (.*) (.*) (.*) (.*) (.*) или чередования, где часто встречающиеся варианты идут не в начале. В результате программистам часто приходится заучивать, какие конструкции не слишком удачны, чтобы избегать их использования, либо применять так называемые оптимизаторы. Но при использовании алгоритма Thompson NFA это не требуется, там нет «дорогих» регулярных выражений.
По эффективности выполнения DFA превосходят NFA, поскольку они могут находиться лишь в одном состоянии одновременно. Любой NFA может быть преобразован в эквивалентный DFA, в котором каждое состояние соответствует списку состояний NFA.
Вот уже рассмотренный выше NFA для ABAB|ABBB:
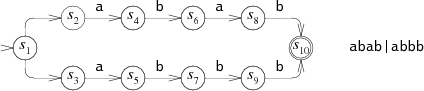
Эквивалентный DFA выглядит так:
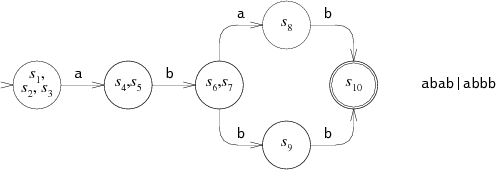
В некотором роде Thompson NFA представляет собой эквивалентный DFA: каждый List соответствует одному из состояний DFA, а функция step на основании списка состояний и следующего искомого символа вычисляет следующее состояние DFA. Алгоритм Томпсона моделирует DFA, реконструируя каждое из состояний по мере необходимости. Но вместо того, чтобы делать это после каждого действия, мы можем кэшировать все списки в резервной памяти. Это помогает в дальнейшем избежать избыточных вычислений, особенно вычисления эквивалентного DFA. Давайте рассмотрим этот подход.
К описанному выше NFA нам нужно добавить менее 100 строк, чтобы получился DFA. Прежде чем внедрять механизм кэширования, сначала нужно объявить новый тип данных для описания состояния DFA:
struct DState
{
List l;
DState *next[256];
DState *left;
DState *right;
};
DState является закэшированной копией списка l. В массиве next хранятся указатели на следующее состояние для каждого возможного символа входных данных: если текущее состояние D, а следующий символ — C, то следующим состоянием будет d->next[c]. Если d->next[c] имеет значение null, значит, следующее состояние ещё не вычислено. Вычислением, записью и возвратом следующего состояния занимается nextstate.
При поиске регулярного выражения d->next[c] обрабатывается циклически, вызывая nextstate для вычисления нового состояния по мере надобности.
int match(DState *start, char *s)
{
int c;
DState *d, *next;
d = start;
for(; *s; s++){
c = *s & 0xFF;
if((next = d->next[c]) == NULL)
next = nextstate(d, c);
d = next;
}
return ismatch(&d->l);
}
Все вычисленные DState нужно сохранить в виде структуры, которая позволит находить их по критерию List. Для этого применяется двоичное дерево, где в качестве ключей используются отсортированные List. По ключу функция dstate возвращает нужное значение:
DState* dstate(List *l)
{
int i;
DState **dp, *d;
static DState *alldstates;
qsort(l->s, l->n, sizeof l->s[0], ptrcmp);
/* look in tree for existing DState */
dp = &alldstates;
while((d = *dp) != NULL){
i = listcmp(l, &d->l);
if(i < 0)
dp = &d->left;
else if(i > 0)
dp = &d->right;
else
return d;
}
/* allocate, initialize new DState */
d = malloc(sizeof *d + l->n*sizeof l->s[0]);
memset(d, 0, sizeof *d);
d->l.s = (State**)(d+1);
memmove(d->l.s, l->s, l->n*sizeof l->s[0]);
d->l.n = l->n;
/* insert in tree */
*dp = d;
return d;
}
Nextstate инициализирует step NFA и возвращает соответствующий DState:
DState*
nextstate(DState *d, int c)
{
step(&d->l, c, &l1);
return d->next[c] = dstate(&l1);
}
Согласно начальному списку NFA, начальным состоянием DFA является соответствующий DState:
DState*
startdstate(State *start)
{
return dstate(startlist(start, &l1));
}
Как и в NFA, l1 является предварительно определённым List.
Хотя значения DState соответствуют определённым состояниям DFA, сам DFA строится, только когда возникает необходимость. Если во время поиска состояние DFA обнаружено, значит, оно пока отсутствует в кэше. В качестве альтернативного решения можно единожды вычислить DFA целиком. Это позволит несколько ускорить работу match, поскольку будет исключён условный переход, но при этом увеличится время запуска и объём используемой памяти.
При построении DFA на лету обратите внимание вот на какой момент, связанный с выделением памяти. Поскольку DState является кэшем функции step, при разрастании кэша dstate может принять решение уничтожить весь DFA. Для реализации подобной политики замещения кэша требуется лишь несколько дополнительных строк кода в dstate и nextstate, а также ещё строк 50 для управления памятью. Скачать пример можно здесь: http://swtch.com/~rsc/regexp/. Кстати, в awk используется аналогичная стратегия, там в кэше хранится не более 32 состояний. Это объясняет падение его производительности начиная с N = 28, как было показано на графике.
Полученные из регулярных выражений NFA отличает хорошая локальность (locality): в большинстве тестов они принимают те же состояния и следуют по тем же переходам снова и снова. Это ещё более повышает важность кэширования, ведь после первого прохода уже не нужно вычислять состояния, достаточно взять их из памяти. В основанных на DFA реализациях может применяться дополнительная оптимизация, ещё больше увеличивающая скорость выполнения.
В настоящих приложениях несколько труднее использовать регулярные выражения, чем в описанных выше реализациях. Здесь мы рассмотрим характерные трудности, возникающие перед разработчиками.
Символьные классы. Являются упрощённым представлением чередования — 0-9, \w или. (точка). Во время компиляции они могут быть преобразованы в чередования, хотя для их явного представления было бы эффективнее добавить новый тип NFA-узла. POSIX задаёт специальные символьные классы наподобие [[:upper:]], меняющие своё значение в зависимости от текущего узла. Трудность работы с ними заключается в определении их значений, а не во внесении этих значений в NFA.
Управляющие последовательности. Синтаксис регулярных выражений должен обрабатывать управляющие последовательности, чтобы можно было искать метасимволы (\(, \), \\ и т. д.), а также задавать специальные символы вроде \n.
Повторение (Counted repetition). Во многих реализациях регулярных выражений используется оператор повторения {N}, где N — точное количество совпадений шаблона. Запись {N, M} означает, что шаблон должен быть найден от N до M раз. {N,} — N и больше раз. В реализациях с рекурсивным бэктрекингом повторения могут осуществляться с помощью циклов. В реализациях на основе NFA и DFA повторения должны представляться в развёрнутом виде: вместо E{3} — EEE, вместо E{3,5} — EEEE?E?, вместо E{3,} — EEE+.
Подвыражения (Submatch extraction). Если РВ используются для разделения или парсинга строк, то бывает полезным выяснить, встречаются ли во входных данных совпадения с подвыражениями. Если в тексте есть совпадение с ([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+), то во многих реализациях РВ можно будет находить совпадения по каждому из заключённых в круглые скобки подвыражений. Например, в Perl:
if(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){
print "date: $1, time: $2\n";
}
Извлечение подвыражений по большей части игнорировалось теоретиками. Быть может, это одна из главных причин использования рекурсивных бэктрекингов. Однако разновидности алгоритма Томпсона могут быть адаптированы для работы с подвыражениями без потери производительности. Это было реализовано ещё в 1985-м, в библиотеке regexp в восьмой версии UNIX, но не получило широкого распространения.
Поиск без привязки (Unanchored matches). Информация в этой статье излагается из расчёта, что поиск РВ производится по всем входным данным. Но в жизни нередко возникают ситуации, когда нам нужно найти лишь часть строки, совпадающую с РВ. В UNIX традиционно возвращается наиболее длинная подстрока из найденных совпадений, начинающаяся ближе всего к началу входных данных. Поиск без привязки является частным случаем подвыражений. Это как если искать .*(E).*, где первая последовательность .* ограничивает поиск самым коротким совпадением.
Нежадные операторы. В традиционной UNIX-реализации при использовании операторов повторения ?, * и + ищется наибольшее возможное количество совпадений РВ целиком. Например, если ведётся поиск по ABCD с операторами (.+)(.+), то первая последовательность (.+) находит совпадение ABC, а вторая — D. Такие операторы называются жадными.
В Perl используются нежадные версии ??, *? и +?.. Они позволяют находить как самые маленькие фрагменты, так и весь набор символов целиком: при поиске по ABCD с операторами (.+?)(.+?) первая комбинация (.+?) найдёт А, а вторая — BCD. Жадность оператора никак не влияет на соответствие РВ всей строке в целом. От неё зависит лишь выбор границ подвыражения. Алгоритм бэктрекинга позволяет использовать простую реализацию нежадных операторов: сначала ищется более короткое совпадение, потом более длинное. Например, в стандартной реализации алгоритм с бэктрекингом при поиске E? сначала старается найти Е, а после обнаружения старается уже не использовать его; при E?? применяется другой порядок действий. Варианты алгоритма Томпсона с использованием подвыражений могут быть адаптированы для применения нежадных операторов.
Утверждения (Assertions). Метасимволы ^ и $ могут использоваться в качестве утверждений по отношению к тексту справа и слева от них. ^ говорит о том, что символ перед ним является началом новой строки. $ утверждает, что следующий символ является окончанием строки. В Perl добавлены и другие утверждения, например \b — предыдущий символ является буквенно-цифровым, а следующий — нет, или наоборот. Также в Perl обобщена идея произвольных условий, называемых предварительными утверждениями (lookahead assertions): (?=re) утверждает, что текст после текущей позиции совпадает с re, но не изменяет саму позицию. (?!re) утверждает, что текст не совпадает с re, в остальном работает аналогично. Утверждения (?<=re) и (?<!re) равнозначны и говорят о совпадении текста перед текущей позицией.
Простые утверждения наподобие ^, $ и \b можно легко применять в NFA, задерживая на один байт процедуру сопоставления для предварительных утверждений. Общие утверждения применять в NFA труднее, но всё же возможно.
Обратные ссылки (Backreferences). Как уже упоминалось выше, пока ни у кого не получилось эффективно реализовать РВ с обратными ссылками. С другой стороны, никто ещё не доказал, что это невозможно сделать. Это НП-полная задача, и если кто-то найдёт решение, то сможет получить приз в миллион долларов. Проще всего вообще не использовать обратные ссылки, как поступили разработчики awk и egrep. Но этот подход больше не практичен: пользователи привыкли полагаться на обратные ссылки, хотя бы время от времени. К тому же они являются частью стандарта POSIX для регулярных выражений. Но даже в этом случае есть смысл использовать для большинства РВ алгоритм Thompson NFA, применяя бэктрекинг лишь в случае необходимости. Лучше всего прибегать к бэктрекингу только для размещения обратных ссылок.
Бэктрекинг с мемоизацией. Мемоизация в Perl используется для предотвращения катастрофического падения производительности при бэктрекинге. В теории всё хорошо, но всё же мемоизация не решает проблему полностью, поскольку её использование требует объёма памяти, сравнимого с произведением размеров текста и РВ. Также мемоизация не решает проблему размера стека, используемого при бэктрекинге. Он линейно зависит от размера текста, и при сопоставлении по длинным строкам возможно исчерпание объёма стека:
$ perl -e '("a" x 100000) =~ /^(ab?)*$/;'
Segmentation fault (core dumped)
$
Наборы символов. Современные реализации РВ должны уметь работать с большими наборами не ASCII-символов как с Unicode. В библиотеке Plan 9 применяется такой подход для внедрения Unicode: во время работы NFA при каждом действии во входных данных используется один Unicode-символ. При этом библиотека разделяет выполнение NFA и декодирование входных данных, поэтому один и тот же код сопоставления берется для работы и с UTF-8, и с Unicode.
Поиск по регулярным выражениям может быть быстрым и простым при условии использования конечных автоматов, известных многие годы. Но в Perl, PCRE, Python, Ruby, Java и многих других языках реализации РВ основаны на рекурсивном бэктрекинге, который хоть и прост, но может работать крайне медленно. При этом реализации с автоматами предоставляют такой же набор возможностей (за исключением обратных ссылок), но работают гораздо быстрее и более предсказуемо.
[1] L. Peter Deutsch and Butler Lampson. An online editor // Communications of the ACM. Vol. 10, Iss. 12 (December 1967). P. 793–799. doi.acm.org/10.1145/363848.363863
[2] Ville Laurikari. NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions // Proceedings of the Symposium on String Processing and Information Retrieval. September 2000. laurikari.net/ville/spire2000-tnfa.pdf
[3] M. Douglas McIlroy. Enumerating the strings of regular languages // Journal of Functional Programming. 2004. № 14. P. 503–518. www.cs.dartmouth.edu/~doug/nfa.ps.gz (preprint)
[4] R. McNaughton and H. Yamada. Regular expressions and state graphs for automata // IRE Transactions on Electronic Computers. Vol. EC-9 (1) (March 1960). P. 39–47.
[5] Paul Pierce. CTSS source listings. www.piercefuller.com/library/ctss.html (Thompson’s QED is in the file com5 in the source listings archive and is marked as 0QED)
[6] Rob Pike/ The text editor sam // Software — Practice & Experience. Vol. 17, № 11 (November 1987. P. 813–845. plan9.bell-labs.com/sys/doc/sam/sam.html
[7] Michael Rabin and Dana Scott. Finite automata and their decision problems // IBM Journal of Research and Development. 1959. № 3. P. 114–125. www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf
[8] Dennis Ritchie. An incomplete history of the QED text editor. www.bell-labs.com/usr/dmr/www/qed.html
[9] Ken Thompson. Programming Techniques: Regular expression search algorithm // Communications of the ACM. Vol. 11, Iss. 6 (June 1968). P. 419–422. doi.acm.org/10.1145/363347.363387 (PDF)
[10] Tom Van Vleck. The IBM 7094 and CTSS. www.multicians.org/thvv/7094.html
