[Перевод] Почему треугольники просты, а тетраэдры сложны21.02.2022 13:16

Как вы думаете, существует ли треугольник с углами 41, 76 и 63 градусов?

Поначалу кажется, что ответ прост. Из уроков геометрии мы знаем, что сумма внутренних углов треугольника равна 180 градусам, и поскольку 41 + 76 + 63 = 180, ответом будет «да».

Но в этом вопросе есть и невидимая поначалу сторона. Теорема о сумме углов треугольника гласит, что для треугольника в плоской евклидовой геометрии сумма внутренних углов равна 180 градусов. Но в нашей задаче не даётся треугольник, а спрашивается, существует ли он. Теорема о сумме углов треугольника не отвечает непосредственно на этот вопрос, однако помогает построить нужный нам треугольник.
Чтобы соответствовать требованиям теоремы о сумме углов треугольника, каждый угол треугольника должен быть меньше 180 градусов, то есть мы всегда можем разместить два из них на одной стороне отрезка прямой. Давайте поместим угол в 41 градусов и угол в 76 градусов на одной из сторон отрезка прямой AB:

Исходящие из A и B лучи не могут быть параллельными, потому что в евклидовой геометрии такие углы, «внутренние для одной стороны», должны быть «смежными», то есть в сумме давать 180 градусов. Но эти углы не имеют такой суммы, то есть лучи не параллельны, а поскольку они не параллельны, они должны пересекаться.

Обозначим их пересечение как C. Теперь у нас есть треугольник и мы можем применить теорему о сумме углов треугольника. Третий угол должен иметь величину 180 − (41 + 76) = 63, поэтому $inline$\triangle A B C$inline$ является именно тем треугольником, который мы ищем.

Это рассуждением можно обобщить, чтобы показать, что любые три величины угла, в сумме дающие 180 градусов, могут составить треугольник, и из этого непосредственно следует, что можно легко найти треугольники, все величины углов которых (в градусах) являются рациональными числами. Давайте начнём с двух положительных рациональных чисел, сумма которых меньше 180; назовём их x и y. Тогда 180 − (x + y) тоже является рациональным числом, а поскольку x + y + (180 − (x + y)) = 180, мы можем составить треугольник с этими тремя рациональными углами.

Несмотря на простоту создания треугольников с рациональными углами, похожая задача в трёх измерениях оказалась настолько сложной, что для её решения лучшим математикам мира потребовались десятки лет. Почему при увеличении размерности на одну эта задача становится настолько сложнее? Поняв это, мы станем ещё больше ценить теорему о сумме углов треугольника.

В схожей задаче в трёх измерениях задействованы тетраэдры — четырёхсторонние фигуры с треугольными гранями. Можно считать их трёхмерными версиями треугольников. В двух измерениях треугольник является простейшей замкнутой фигурой, которую можно составить из плоских сторон, и для этого требуется три отрезка прямых. В трёх измерениях тетраэдр — простейшая замкнутая фигура, которую можно составить из плоских сторон, и для этого требуется четыре треугольных грани.

Четыре треугольных грани тетраэдра схожи с тремя сторонами треугольника. Но как нам воспринимать углы? Можно представить «сплошной угол» на каждой из четырёх вершин тетраэдра. Но в интересующем нас вопросе задействуются «двугранные углы», образуемые пересекающимися гранями.

Если начертить две пересекающиеся плоскости, обнаружится множество разных углов, которые можно измерить. Какой из них выбрать, для задания двугранного угла?

Ответ заключается в том, чтобы поворачивать пересекающиеся грани, пока они не будут похожи на двухмерный угол.

Именно этот угол мы ассоциируем с двугранным углом.

В тетраэдре каждая из четырёх граней пересекается со всеми остальными гранями, образуя шесть рёбер и шесть двугранных углов. Десятилетиями математики задавались вопросом, какие тетраэдры имеют шесть рациональных двугранных углов. Как и говорилось ранее, угол считается рациональным, если его угловая мера является рациональным числом. Это эквивалент того, что его мера в радианах является рациональным числом, кратным $inline$\pi$inline$ (чтобы увидеть эквивалентность, можно вспомнить, что для преобразования из градусов в радианы мы умножаем угловую меру на $inline$\frac{\pi}{180^{\circ}}$inline$, то есть если угловая мера рациональна, то радиальная мера будет являться кратным $\pi$ рациональным числом, и наоборот.)

Мы уже знаем, насколько легко составлять треугольники с рациональными углами, но в случае тетраэдров задача гораздо сложнее. Рассмотрим следующий простой тетраэдр $O A B C$ , образованный срезом угла куба.

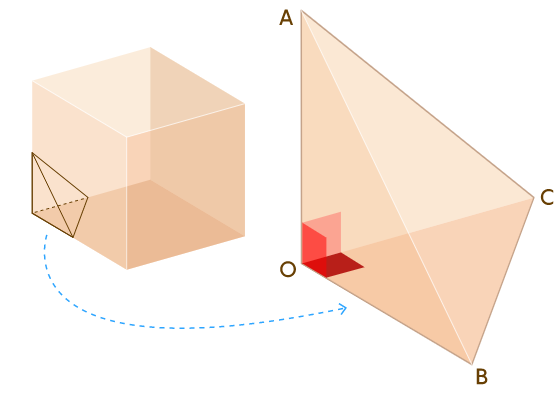
Мы сразу же видим, что три двугранных угла в этом тетраэдре являются прямыми, поскольку они образованы гранями куба. Удобно обозначить каждый двугранный угол по его ребру, так что в этом тетраэдре двугранные углы при $OA$ , $OB$ и $OC$ являются прямыми.

Если мы срежем куб так, что $OA$ = $OB$ = $OC$ , двугранные углы при $AB$ , $AC$ и $BC$ будут равными. Давайте срежем куб так, что $OA$ = $OB$ = $OC$ = 1, а затем вычислим двугранный угол при $BC$ . Чтобы измерить двугранный угол, нужно начертить отрезки из $O$ и $A$ к средней точке $BC$ . Давайте обозначим эту точку $M$ .

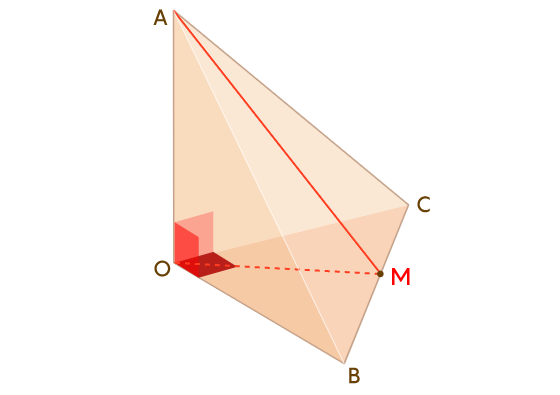
Если повернуть тетраэдр так, чтобы смотреть на двугранный угол при $BC$ сбоку, то мы увидим $\angle A M O$ , имеющий ту же величину. Чтобы измерить $\angle A M O$ , нам нужны длины $OA$ и $OM$ . Мы уже знаем, что $OA$ = 1, а чтобы найти $OM$ , нам достаточно внимательнее присмотреться к треугольнику $\Delta O C B$ .

Так как $\angle B O C$ является прямым, это прямоугольный треугольник, поэтому мы можем воспользоваться теоремой Пифагора, чтобы вычислить, что $BC$ = $\sqrt{2}$ . А поскольку $M$ является средней точкой $BC$ , мы знаем, что $MC$ = $\frac{\sqrt{2}}{2}$ . Но кроме того, что $\Delta O C B$ является прямоугольным треугольником, он также является равнобедренным, поскольку $OB$ = $OC$ . Это делает его треугольником 45–45–90, то есть $\angle OBC$ и $\angle OCB$ равны 45 градусам. То, что $\Delta O C B$ является равнобедренным, гарантирует, что $OM$ перпендикулярна $BC$ , что делает $\Delta O M C$ тоже прямоугольным треугольником. Но если величина $\angle O M C$ = 90°, а величина $\angle O C B$ = 45°, тогда теорема о сумме углов треугольника говорит нам, что $\angle M O C$ = 45°. Из-за этого маленький треугольник $\Delta O M C$ является равнобедренным, то есть $OM$ = $MC$ = $\frac{\sqrt{2}}{2}$ .

Теперь мы наконец готовы найти величину $\angle A M O$ .

В $\Delta A M O$ мы знаем, что $AO$ = 1, а $OM$ = $\frac{\sqrt{2}}{2}$ , а поскольку $\angle A O M$ является прямым, мы можем воспользоваться тригонометрией. В прямоугольном треугольнике тангенс угла равен соотношению противоположной и соседней сторон:

$\tan \angle A M O = \frac{1}{\frac{\sqrt{2}}{2}} = \frac{2}{\sqrt{2}} = \sqrt{2}$

То есть величиной $\angle A M O$ является арктангенс $\sqrt{2}$ . Он оказывается иррациональным числом, поэтому это не пример рационального тетраэдра, поскольку три из его углов не рациональны. Но хотя это не то, что мы искали, данный иррациональный тетраэдр может сообщить нам нечто важное о поисках рациональных тетраэдров.

Чтобы понять это, давайте найдём приблизительную сумму двугранных углов в нашем иррациональном тетраэдре. При помощи калькулятора или тригонометрической таблицы мы выясним, что приблизительная величина $\angle A M O$ составляет примерно 54,74 градуса.

Теперь мы можем суммировать шесть двугранных углов тетраэдра $OABC$ : три из них являются прямыми (с величиной 90 градусов), а другие три равнобедренны с только что найденным нами углом. Следовательно, сумма шести двугранных углов этого тетраэдра приблизительно равна 3 × 90° + 3 × 54,74°≈ 434,22°.

И здесь дело принимает неожиданный поворот. Давайте вернёмся к кубу и вместо того, чтобы срезать его так, что $OA$ = $OB$ = $OC$ , представим, что мы делаем очень тонкий срез с угла.

Этот новый тетраэдр тоже будет иметь три 90-градусных двугранных угла при $OP$ , $OC$ , $OB$ , но другие двугранные углы изменились. Угол при $BC$ теперь выглядит довольно маленьким, а углы при $PB$ и $PC$ больше походят на углы при $OB$ и $OC$ .

На самом деле, если продолжать делать всё более тонкие срезы, $P$ будет приближаться к $O$ , двугранный угол $BC$ будет стремиться к 0 градусов, а двугранные углы при $PB$ и $PC$ будут стремиться к 90 градусам. Посмотрим на приблизительную сумму углов:

$90° + 90° + 90° + 90° + 90° + 0° = 450°$

При приближении $P$ к $O$ сумма шести двугранных углов тетраэдра стремится к 450°. Это значит, что сумма углов меняется! В нашем исходном тетраэдре $OABC$ сумма двугранных углов была примерно равна 432°, но при изменении углов общая сумма меняется. Тетраэдр в каком-то смысле может быть 3D-версией треугольника, но в одном он сильно отличается: не существует теоремы о сумме двугранных углов тетраэдра, гарантирующей, что сумма углов будет постоянной.

Оказывается, в лучшем случае мы можем гарантировать, что сумма шести двугранных углов тетраэдра находится в интервале от 360 до 540 градусов. А если вы ищете тетраэдры с рациональными двугранными углами, это становится проблемой. Нельзя просто выбрать пять рациональных углов и быть уверенным, что шестой автоматически будет рациональным, потому что, в отличие от случая с треугольником, мы понятия не имеем, какой должна быть сумма.

Хуже того, мы даже не можем быть уверенными, что любые шесть углов могут быть двугранными углами тетраэдра. Рассмотрим пять прямых углов и один острый. Сумма этих шести углов находится в интервале от 450 до 540 градусов, что лежит в рамках приемлемого для тетраэдра интервала. Но тетраэдра с такими шестью величинами углов не существует. Если пять из шести двугранных углов являются прямыми, то одна из граней должна иметь три прямых двугранных угла. Но если это так, то такие грани не замыкаются и не образуют тетраэдр: как параллельные линии они никогда не пересекаются.

Грани, пересекающиеся в трёх прямых двугранных углах, могут быть частью пятигранной призмы, но не тетраэдра.

Следовательно, для решения задачи поиска всех возможных рациональных тетраэдров требуется больше, чем просто найти пять или шесть рациональных чисел с определённой суммой. Среди прочего, для этого требуется решить уравнение с 105 членами, источником которого стала статья 1976 года, написанная Джоном Конвеем и Антонией Джонс. Группа математиков справилась с этой задачей в 2020 году, и результатом стала полная классификация всех рациональных тетраэдров.

Теорема о сумме углов треугольников — одна из множества причин восхищаться красотой и изяществом треугольников. Отсутствие такой теоремы для тетраэдров — причина для того, чтобы ценить их красоту и сложность в пространстве на одно измерение больше.

Упражнения

1. Какова сумма двугранных углов в кубе?

2. Какова (приблизительная) сумма шести двугранных углов в правильном тетраэдре?

3. Представьте правильный тетраэдр, стоящий на столе. Если опускать верхнюю вершину к нижней грани, как будет меняться сумма шести двугранных углов?

4. Могут ли какие-нибудь четыре угла с суммой 360 градусов быть углами четырёхугольника?

Ответ на упражнение 1

У куба 12 ребёр, то есть 12 двугранных углов. Каждый из них является прямым, то есть сумма равна 12 × 90° = 1080°.

Ответ на упражнение 2

Все шесть двугранных углов являются равнобедренными, поэтому мы можем использовать соответствующий прямоугольный треугольник, чтобы найти величину одного из двугранных углов.

Все грани правильного тетраэдра являются равносторонними треугольниками, поэтому медиана (отрезок от вершины до средней точки) грани имеет длину $\frac{\sqrt{3}}{2} s$ , где $s$

— это длина стороны. Это гипотенуза нужного нам треугольника. Высота, опущенная из верхней вершины тетраэдра, пересекает нижний равносторонний треугольник в его геометрическом центре, который, как известно, находится в $\frac{1}{3}$ медианы от средней точки, поэтому эта сторона данного треугольника равна $\frac{1}{3}$ × $\frac{\sqrt{3}}{2} s$ . Двугранный угол — это угол между двумя этими сторонами, поэтому он равен обратному косинусу $\frac{\frac{1}{3} \times \frac{\sqrt{3}}{2} s}{\frac{\sqrt{3}}{2} s}$ = $\frac{1}{3}$ . Так как $\arccos \frac{1}{3}$ ≈ 70,53°, сумма шести (равнобедренных) двугранных углов правильного тетраэдра приблизительно равна 6 × 70,53° ≈ 423,18°.

Ответ на упражнение 3

Так как тетраэдр становится более плоским, три двугранных угла на нижней грани стремятся к нулю, а три остальных двугранных угла стремятся к 180 градусам, что даёт сумму 3 × 0 + 3 × 180° = 540°. И это максимально возможная сумма двугранных углов в тетраэдре. Чтобы достичь наименьшей возможной суммы, представим, что сдвигаем две противоположные грани друг к другу: при этом четыре угла будут стремиться к 0, а два — к 180 градусам.

Ответ на упражнение 4

Да. Допустим, величины равны a, b, c и d, при этом a + b + c + d = 360. Допустим, что a и b меньше или равны c и d. Разделим c на c1 и c2, а d — на d1 и d2 так, что c = c1 + c2, d = d1 + d2, a + c1 + d1 = 180 и b + c2 + d2 = 180 (мы можем сделать это множеством разных способов). Воспользуемся двумя множествами углов для составления двух треугольников, выровняв их так, чтобы стороны, противоположные углам a и b, были равнобедренными. Теперь соединим их так, чтобы c1 и c2 сливались, образуя c, а d1 и d2 сливались, образуя d, и так мы получим четырёхугольник с углами a, b, c и d.

Интересная задача: разобраться, можно ли всегда составить четырёхугольник с углами в определённом порядке.