[Перевод] Перевод книги Эндрю Ына «Страсть к машинному обучению» Главы 44 — 46
предыдущие главы
Предположим, вы разрабатываете систему распознавания речи. Система получает на вход запись голоса A и вычисляет некоторую величину A (S), оценивающую правдоподобность того, что этот аудиоклип соответствует предложению S. Например, вы можете попытаться оценить величину A (S) = P (S|A), как вероятность того, что корректной выходной транскрипцией будет предложение S, при условии, что входным звуком был A.
Какой бы способ оценки величины A (S) вы не выбрали, задача состоит в том, чтобы найти английское предложение S, при котором эта величина будет максимальной: 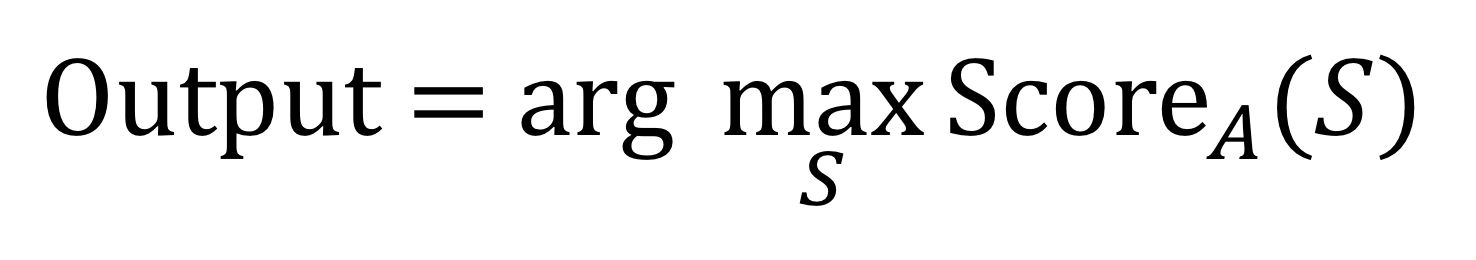
Как подойти к вычислению «arg max» в этой формуле? Допустим в английском языке 50000 слов, из них можно составить
предложений длины N — слишком много для того, чтобы их можно было все перебрать, какими бы вычислительными мощностями мы не располагали.
Таким образом, нужно найти приближенный алгоритм, позволяющий найти значение S, оптимизирующее (максимизирующее) величину A (S). Примером такого алгоритма может служить «лучевой алгоритм», который сохраняет только K главных кандидатов в процессе поиска. (Для целей этой главы не нужно в деталях понимать, как работает «лучевой алгоритм»). Подобные алгоритмы не дают полной гарантии, что будет найдено значение S, соответствующее максимуму оценки A (S).
Предположим, что клип A содержит запись кого-то, говорящего «Я люблю машинное обучение». А система выдает ошибочное: «Я люблю роботов».
Существуют два источника ошибки:
- Не верно работающий алгоритм поиска. Приближенный алгоритм поиска (лучевой алгоритм) не нашел значение S, максимизирующее показатель A (S).
- Плохо работающая целевая функция (функция оценки). Наши оценки величины A (S) = P (S|A) были неточными. В частности, выбор оценки A (S) не позволил распознать «я люблю машинное обучение» в качестве правильной транскрипции.
В зависимости от источника ошибки, нужно по-разному расставлять приоритеты. В первом случае нужно работать над улучшением алгоритма приближенного поиска. Во втором необходимо улучшать алгоритм, оценивающий A (S).
Столкнувшись с таким типом проблем, одни исследователи случайным образом решат заняться алгоритмом приближенного поиска; другие скорее возьмутся за улучшение целевой функции A (S). Но если неизвестно, откуда проистекает ошибка, усилия могут быть потрачены впустую.
Как более системно подойти к выбору направления приложения усилий?
Обозначим выходную транскрипцию системы («Я люблю роботов»), как Sout. А правильную («Я люблю машинное обучение»), как S*. Чтобы понять, мы имеем дело с первым или со вторым источником ошибки из выше приведенных, можно выполнить тест для проверки оптимизации (The Optimization Verification test): сначала нужно посчитать значение ScoreA(S*) и значение ScoreA(Sout), затем сравнить ScoreA(S*) и ScoreA(Sout).
Случай 1: ScoreA(S*) > ScoreA(Sout)
В этом случае алгоритм правильно предпочел S*, дав ему более высокую оценку, чем Sout. Тем не менее, система вывела Sout, а не S*. Это говорит о том, что алгоритм поиска не может найти значение S, при котором показатель A (S) будет максимальным. Тест для проверки оптимизации (The Optimization Verification test) сигнализирует, что алгоритм поиска работает не корректно, и следует сосредоточиться на нем. Например, можно попробовать увеличить ширину луча в «лучевом алгоритме» (beam search).
Случай 2: ScoreA(S*) ≤ ScoreA(Sout).
В этом случае виноват алгоритм вычисления целевой функции ScoreA(.): Он не может предпочесть правильную транскрипциюS* и более высоко оценивает Sout. Тест для проверки оптимизации (The Optimization Verification test) указывает на проблему с этим алгоритмом. Таким образом, необходимо заняться поиском лучших подходов к обучению алгоритма или того, как он соотносит ScoreA(S) с различными предложениями S.
Мы обсудили только один пример. Чтобы применить Тест для проверки оптимизации (The Optimization Verification test) на практике, необходимо применить этот подход к множеству ошибок работы системы на валидационной выборке. Для каждой ошибки нужно проверить, будет ли ScoreA(S*) > ScoreA(Sout). Ошибка, для которой выполняется это неравенство, помечается, как ошибка алгоритма поиска. Ошибка, для которой ScoreA(S*) ≤ ScoreA(Sout) совершается алгоритмом оценки целевой функции ScoreA(.).
Например, предположим, что 95% ошибок связаны с алгоритмом оценки целевой функции ScoreA(.), и только 5% из-за алгоритма поиска. В этом случае, как бы мы не улучшили алгоритм поиска, это устранит не более ~ 5% ошибок системы. Целесообразнее сосредоточиться на улучшении алгоритма, оценивающего ScoreA(.).
Тест для проверки оптимизации (the Optimization Verification test) применим в тех случаях, когда, при некотором x на входе, понятно, как посчитать значение оптимизационной функции x (y), показывающей, насколько результат на выходе y соответствует входящему x и одновременно используется некий приблизительный алгоритм, при помощи которого мы пытаемся найти arg maxyScorex(y), при этом есть опасение, что алгоритм поиска иногда не находит максимум. В предыдущем примере распознавания речи на вход подавался аудиоклип x=A, а на выходе возвращалась транскрипция y=S.
Предположим, что y* — «правильный» результат, но алгоритм выдает отличный от него yout. В этом случае ключевым для поиска проблемы является оценка неравенства Scorex(y*) > Scorex(yout). Если это неравенство выполнено, то проблема связана с алгоритмом оптимизации. Можно вернуться к предыдущей главе, чтобы убедиться в понимании того откуда это следует. В противном случае проблема в работе алгоритма, оценивающего Scorex(y).
Давайте рассмотрим еще один пример. Допустим, вы создаете систему машинного перевода с китайского на английский. Ваша система получает на вход китайское предложение C и вычисляет некоторое значение ScoreC(E) для каждого возможного английского перевода E. Например, в качестве оценки ScoreC(E) = P (E|C), можно использовать вероятность английского предложения E, при условии, что на вход было подано китайское предложение C.

Однако, набор всех возможных английских предложений слишком велик, поэтому приходится использовать некий эвристический алгоритм поиска.
Предположим, алгоритм выдает неверный перевод Eout вместо правильного E*. Используя тест для проверки оптимизации, мы должны посмотреть на неравенство ScoreC(E*) > ScoreC(Eout). Если оно выполнено, то алгоритм ScoreC(.) правильно предпочел E* в сравнение с Eout; таким образом, ошибка системы связана с алгоритмом предварительного поиска. В противном случае проблема у алгоритма, вычисляющего ScoreC(.).
Это очень распространенный «шаблон проектирования» при разработке систем искусственного интеллекта: сначала обучить оценивающую функцию (approximate scoring function) Scorex(.), А затем использовать приблизительный алгоритм максимизации (approximate maximization algorithm). Если вы будете использовать этот шаблон, то вам будет полезен Тест для проверки оптимизации (The Optimization Verification test) в процессе поиска источника ошибок его работы.

Предположим, вы используете машинное обучение, чтобы научить вертолет совершать сложные маневры. На картинке приведена замедленная съемка вертолета, управляемого компьютерным контроллером, совершающего посадку с выключенным двигателем.
Такой манёвр называется «авторотацией». Он позволяет вертолетам приземляться, даже если их двигатель внезапно выйдет из строя. Этот маневр входит в программу подготовки пилотов-людей. Необходимо, используя алгоритмы машинного обучения, научить вертолет безопасно приземляться.
Обучение с подкреплением подразумевает использование «функции вознаграждения» R (.), которая оценивает каждую из возможных траекторий посадки вертолета T. Например, если T приводит к крушению вертолета, то R (T) = -1000 — «наградой» будет большая отрицательная величина. Траекторию T, приводящую к безопасной посадке, функция вознаграждения R (T) оценит в положительную величину, точное значение которой варьируется в зависимости от того, насколько плавной была посадка. Функция вознаграждения R (.), как правило выбирается вручную, чтобы количественно разделить различные траектории T. Данная функция должна оценивать, была ли при посадке тряска, приземлился ли вертолет точно в заданном месте, насколько приземление было безопасным для пассажиров. Разработка подходящей функции вознаграждения — непростая задача.
После того, как функция вознаграждения R (T) выбрана, задача алгоритма обучения с подкреплением состоит в том, чтобы вертолет двигался по такой траектории Т, которая обеспечивает максимум функции вознаграждения maxTR (T). При этом алгоритмы обучения с подкреплением используют различные приближения и могут не достигать этого максимума.
Предположим, функция вознаграждения R (.) выбрана, обученный алгоритм запущен. Однако, качество его работы много хуже, чем у пилота-человека — при приземлении вертолет трясет и приземление выглядит намного менее безопасным.
Как определить — ошибки при приземлении связаны с тем, что алгоритм, обученный с подкреплением, не может придерживаться траектории Т, дающей максимум функции вознаграждения maxTR (T) или проблемы в самой функции вознаграждения, которой следует алгоритм, пытаясь найти идеальный компромисс между тряской при посадке и точностью приземления?
Чтобы применить Тест для проверки оптимизации (Optimization Verification test), определим Thuman, как траекторию, по которой приземляется пилот-человек, и пусть Tout траектория алгоритма. Как мы уже говорили, Thuman превосходит по качеству Tout. Для нашего теста ключевым является вопрос: верно ли, что R (Thuman) > R (Tout)?
Вариант 1: если это неравенство выполняется, то функция вознаграждения R (.) правильно оценивает, что Thuman превосходит Tout., но наш алгоритм, обученный с подкреплением, находит траекторию Tout, не являющеюся максимум функции вознаграждения. Следовательно, надо работать над улучшением алгоритма обучения с подкреплением.
Вариант 2: неравенство не выполняется: R (Thuman) ≤ R (Tout). Это означает, что R (.) оценивает Thuman ниже, чем Tout, несмотря на то, что Thuman лучшая траектория. В этом случае нужно заняться улучшением R (.), чтобы лучше сбалансировать параметры от которых зависит качество приземления.
Многие приложения машинного обучения имеют «шаблон» оптимизации функции приблизительной оценки Scorex(.) с использованием приближенного алгоритма поиска. Иногда нет заданного ввода x, тогда оценивается только Score (.). В примере с вертолетом оценивалась функция вознаграждения Score (T)=R (T), а алгоритмом оптимизации (optimization algorithm) служил алгоритм, обученный с подкреплением, пытающийся реализовать хорошую траекторию T.
Одно из различий между этим и более ранними примерами состоит в том, что качество алгоритма сравнивается не с «оптимальным» результатом, а с траекторией человека Thuman. Мы предполагали, что Thuman достаточно хорошая, пусть даже не оптимальная. В общем, до тех пор, пока у вас есть некоторый результат y* (в данном примере, Thuman), который превосходит качество работы системы — даже если он не «оптимальный», тест для проверки оптимизации (Optimization Verification test) укажет, что более перспективно: улучшать алгоритм оптимизации или функцию оценки.
продолжение следует
