[Перевод] Оптимальная игра в 2048 с помощью марковского процесса принятия решений24.04.2018 08:03

В предыдущей статье про 2048 мы использовали цепи Маркова, чтобы выяснить, что в среднем для победы нужно не менее 938,8 ходов, а также исследовали с помощью комбинаторики и полного перебора количество возможных конфигураций поля игры.

В этом посте мы используем математический аппарат под названием «марковский процесс принятия решений» для нахождения доказуемо оптимальных стратегий игры 2048 для полей размером 2×2 и 3×3, а также на доске 4×4 вплоть до тайла 64. Например, вот оптимальный игрок в игру 2×2 до тайла 32:

GIF

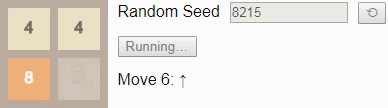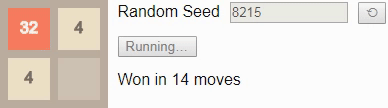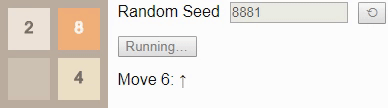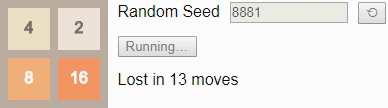
Случайное начальное число (random seed) определяет случайную последовательность тайлов, добавляемых игрой на поле. «Стратегия» игрока задаётся таблицей, называемой алгоритмом (policy). Она сообщает нам, в каком направлении нужно сдвигать тайлы в любой возможной конфигурации поля. В этом посте мы рассмотрим способ создания алгоритма, оптимального в том смысле, что он максимизирует шансы игрока на получение тайла 32.

Оказывается, что в игре 2×2 до тайла 32 очень сложно выиграть — даже если играть оптимально, игрок выигрывает только примерно в 8% случаев, то есть игра оказывается не особо интересной. Качественно игры 2×2 сильно отличаются от игр 4×4, но они всё равно полезны для знакомства с основными принципами.

В идеале мы хотим найти оптимальный алгоритм для полной игры на поле 4×4 до тайла 2048, но как мы убедились из предыдущего поста, количество возможных конфигураций поля очень велико. Поэтому невозможно создать оптимальный алгоритм для полной игры, по крайней мере, с помощью используемых здесь методов.

Однако мы можем найти оптимальный алгоритм для укороченной игры 4×4 до тайла 64, и, к счастью, мы увидим, что оптимальная игра на полях 3×3 качественно выглядит похожей на некоторые успешные стратегии полной игры.

Код (исследовательского качества), на котором основана эта статья, выложен в открытый доступ.

Марковские процессы принятия решений для 2048

Марковские процессы принятия решений (MDP) — это математическая основа моделирования и решения задач, в которой нам необходимо предпринять последовательность взаимосвязанных решений в условиях неопределённости. Таких задач полно в реальном мире, и MDP находят активное применение в экономике, финансовом деле и в искусственном интеллекте. В случае 2048 последовательность решений — это направление перемещения тайлов в каждом ходе, а неопределённость возникает потому, что игра добавляет тайлы на поле случайным образом.

Чтобы представить игру 2048 в виде MDP, нам нужно записать её определённым образом. В него входят шесть основных концепций: состояния, действия и вероятности перехода кодируют динамику игры; вознаграждения, значения и алгоритмы используются для фиксации целей игрока и способов их достижения. Чтобы развить эти шесть концепций, мы возьмём в качестве примера наименьшую нетривиальную игру, похожую на 2048, которая играется на поле 2×2 только до тайла 8. Давайте начнём с первых трёх концепций.

Состояния, действия и вероятности перехода

Состояние фиксирует конфигурацию поля в заданный момент игры, указывая значение тайла в каждой из клеток поля. Например, — это возможное состояние в игре на поле 2×2. Действие — это перемещение влево, вправо, вверх или вниз. Каждый раз, когда игрок совершает действие, процесс переходит в новое состояние.

Вероятности перехода кодируют динамику игры, определяя состояния, которые с большей вероятностью будут следующими, с учётом текущего состояния и действия игрока. К счастью, мы можем точно узнать, как работает 2048, прочитав её исходный код. Самым важным¹ является процесс, который использует игра для размещения на поле случайного тайла. Этот процесс всегда одинаков: выбираем свободную клетку с одинаковой вероятностью и добавляем новый тайл или со значением 2 с вероятностью 0,9, или со значением 4 с вероятностью 0,1.

В начале каждой игры с помощью этого процесса на поле добавляются два тайла. Например, одним из таких возможных начальных состояний является такое: . Для каждого возможного в этом состоянии действия, а именно Left, Right, Up и Down, возможные следующие состояния и соответствующие вероятности перехода имеют следующий вид:

На этой схема стрелки обозначают каждый возможный переход в последующее состояние справа. Вес стрелки и метка обозначают соответствующую вероятность перехода. Например, если игрок сдвигает тайлы вправо (R), то оба тайла 2 сдвигаются к правому краю, оставляя слева две свободные клетки. Новый тайл будет с вероятностью 0,1 тайлом 4, и может появиться или в верхней левой, или в нижней левой клетке, то есть вероятность состояния равна $0.1 \times 0.5 = 0.05$ .

Из каждого из этих последующих состояний мы можем рекурсивно продолжать этот процесс перебора возможных действий и каждого из их последующих состояний. Для возможными последующими состояниями являются такие:

Здесь сдвиг вправо невозможен, поскольку ни один из тайлов не может сдвинуться вправо. Более того, если игрок достигнет последующего состояния , выделенного красным, то он проиграет, поскольку из этого состояния невозможно выполнить допустимых действий. Это произойдёт, если игрок выполнит сдвиг влево, а игра разместит тайл 4, что произойдёт с вероятностью 0,1; из этого можно предположить, что сдвиг влево не является наилучшим действием в этом состоянии.

Ещё один последний пример: если игрок сдвинется вверх, а не влево, то одним из возможных последующих состояний будет , и если мы переберём все допустимые действия и последующие состояния из этого состояния, то мы сможем увидеть, что сдвиг влево или вправо приведёт тогда к тайлу 8, что означает нашу победу (выделенную зелёным):

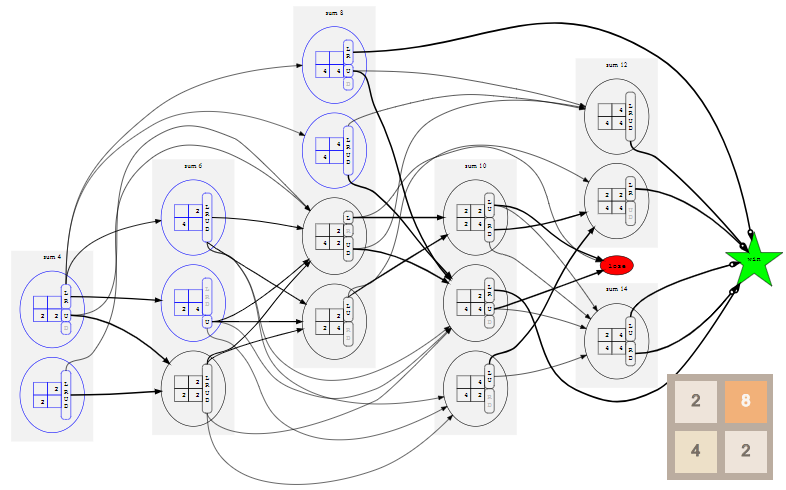
Если мы повторим этот процесс для всех возможных начальных состояний и всех их возможных последующих состояний, и так далее рекурсивно, пока не достигнем состояния выигрыша или проигрыша, то сможем построить полную модель со всеми возможными состояниями, действиями и их вероятностями перехода. Для игры 2×2 до тайла 8 эта модель выглядит так (нажмите для увеличения; возможно придётся прокрутить страницу вниз):

Чтобы сделать схему поменьше, все состояния проигрыша нужно свести к единому состоянию lose, показанному красным овалом, а все выигрышные состояния аналогичным образом свести к единому состоянию win, показанному зелёной звездой. Это возможно, потому что на самом деле нас не интересует, как именно выиграл или проиграл игрок, а важен сам результат.

Игра приближённо протекает на схеме слева направо, потому что состояния упорядочены в «слои» по сумме своих тайлов. Полезное свойство игры заключается в том, что после каждого действия сумма тайлов на поле увеличивается на 2 или на 4. Так получается потому, что слияние тайлов не изменяет сумму тайлов на поле, а игра всегда добавляет или 2, или 4. Возможные начальные состояния, которые являются слоями с суммой 4, 6 и 8, показаны синим.

Даже в модели такого минимального примере 70 состояний и 530 переходов. Однако, можно значительно снизить эти значения, заметив, что многие из перечисленных нами состояний тривиально связаны поворотами и отражениями, как описано в Приложении А. На практике это наблюдение очень важно для уменьшения размера модели и её эффективного решения. Кроме того, оно позволяет создавать более удобные схемы, но для перехода ко второму набору концепций марковского процесса принятия решений это не обязательно.

Вознаграждения, значения и алгоритмы

Чтобы завершить спецификацию модели, нам нужно закодировать каким-то образом тот факт, что цель игрока заключается в достижении состояния win2. Мы сделаем это, определив вознаграждения. В общем случае при каждом переходе MDP в состояние игрок получает вознаграждение, зависящее от состояния. Мы присвоим вознаграждению за переход в состояние win значение 1, а за переход в другие состояния — значение 0. То есть единственный способ получить вознаграждение — достичь состояния выигрыша3.

Теперь, когда у нас есть модель MDP игры, описанная относительно состояний, действий, вероятностей перехода и вознаграждений, мы готовы к её решению. Решение MDP называется алгоритмом. По сути, это таблица, в которой для каждого возможного состояния указано действие, которое нужно совершить в этом состоянии. Решить MDP — значит найти оптимальный алгоритм, то есть такой, который позволяет игроку со временем получить как можно большее вознаграждение.

Чтобы сделать её точной, нам нужна последняя концепция MDP: значение состояния в соответствии с заданным алгоритмом — это ожидаемое вознаграждение, которое получит игрок, если начнёт с этого состояния и затем будет следовать алгоритму. Для объяснения этого необходимы некоторые записи.

Пусть $S$ — это множество состояний, и для каждого состояния $s \in S$ $A_s$ будет множеством действий, допустимых в состоянии $s$ . Пусть $\Pr(s’ | s, a)$ обозначает вероятность перехода в каждое последующее состояние $s’ \in S$ , учитывая, что процесс находится в состоянии $s \in S$ и игрок совершает действие $a \in A_s$ . Пусть $R(s)$ обозначает вознаграждение за переход в состояние $s$ . Наконец, пусть $\pi$ означает алгоритм, а $\pi(s) \in A_s$ обозначает действие, которое нужно совершить в состоянии $s$ , чтобы следовать алгоритму $\pi$ .

Для заданного алгоритма $\pi$ и состояния $s$ значение состояния $s$ согласно $\pi$ равно

$V^\pi(s) = R(s) + \gamma \sum_{s’} \Pr(s’ | s, \pi(s)) V^\pi(s’)$

где первый член — это мгновенное вознаграждение, а суммирование даёт ожидаемое значение последующих состояний при условии, что игрок будет продолжать следовать алгоритму.

Коэффициент $\gamma$ — это коэффициент обесценивания, который замещает значение мгновенного вознаграждения на значение ожидаемого в будущем вознаграждения. Другими словами, он учитывает стоимость денег с учётом фактора времени: вознаграждение сейчас обычно стоит больше, чем то же вознаграждение позже. Если $\gamma$ близок к 1, то это означает, что игрок очень терпелив: он не против подождать будущего вознаграждения; аналогично, меньшие значения $\gamma$ означают, что игрок менее терпелив. Пока мы присвоим коэффициенту обесценивания $\gamma$ значение 1, что соответствует нашему предположению о том, что игрока волнует только победа, а не время, которое для неё потребуется 4.

Так как же нам найти алгоритм? В каждом из состояний мы хотим выбирать действие, максимизирующее ожидаемое будущее вознаграждение:

$\pi(s) = \mathop{\mathrm{argmax}}\limits_{a \in A_s} \left\{ \sum_{s’} \Pr(s’ | s, a) V^\pi(s’) \right\}$

Это даёт нам два связанных уравнения, которые мы можем решить итеративно. То есть выбрать исходный алгоритм, который может быть очень простым, вычислить значение каждого состояния в соответствии с этим простым алгоритмом, а затем найти новый алгоритм на основании этой функции значений, и так далее. Примечательно, что в очень ограниченных технических условиях такой итеративный процесс гарантированно сойдётся к оптимальному алгоритму $\pi^*$ и оптимальной функции значений $V^{\pi^*}$ относительно этого оптимального алгоритма.

Такой стандартный итеративный подход хорошо срабатывает для моделей MDP игр на поле 2×2, но не подходит для моделей игр 3×3 и 4×4, которые имеют гораздо больше состояний, а потому потребляют гораздо больше памяти и вычислительных мощностей. К счастью, оказывается, что мы можем воспользоваться структурой наших моделей 2048 для гораздо более эффективного решения этих уравнений (см. Приложение Б).

Оптимальная игра на поле 2×2

Теперь мы готовы увидеть оптимальные алгоритмы в действии! Если ввести начальное число 42 и нажмёте на кнопку Start в оригинале статьи, то достигнете тайла 8 за 5 ходов. Начальное число определяет последовательность новых тайлов, размещаемых игрой; если выбрать другое начальное число, нажав на кнопку ⟲, то (обычно) игра будет развиваться иначе.

GIF

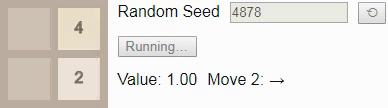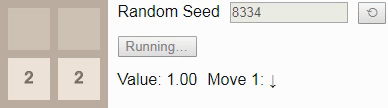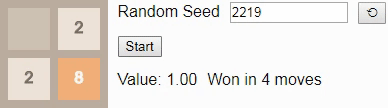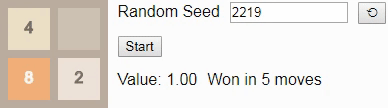
В игре 2×2 до тайла 8 смотреть особо не на что. Если игрок следует оптимальному алгоритму, то всегда будет выигрывать. (Как мы видели выше при построении вероятностей перехода, если игрок играет неоптимально, то есть возможность проигрыша.) Это отражается в том, что значение состояния на протяжении всей игры остаётся равным 1.00 — при оптимальной игре есть хотя бы одно действие в каждом достижимом состоянии, которое ведёт к победе.

Если мы вместо этого попросим игрока сыграть до тайла 16, то даже при оптимальной игре победа уже не будет гарантирована. В этом случае при игре до тайла 16 выбор нового начального числа должно приводить к победе в 96% случаев, поэтому мы в качестве начального числа выбрали одно из тех немногих, что ведут к проигрышу.

GIF

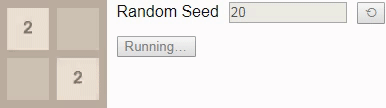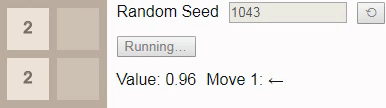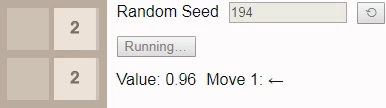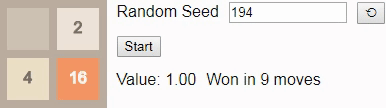
В результате присвоения коэффициенту обесценивания $\gamma$ значения 1 значение каждого состояния сообщает нам вероятность победы из этого состояния. Здесь значение начинается с 0.96, а затем постепенно снижается до 0.90, потому что исход зависит от того, будет ли следующий тайл иметь значение 2. К сожалению, игра выставляет тайл 4, поэтому игрок проигрывает, несмотря на оптимальную игру.

Наконец, мы ранее установили, наибольшим достижимым тайлом на поле 2×2 является тайл 32, поэтому давайте посмотрим на оптимальный алгоритм. Здесь вероятность выигрыша падает всего до 8%. (Это та же игра и тот же алгоритм, использованный во введении, но теперь интерактивные.)

GIF

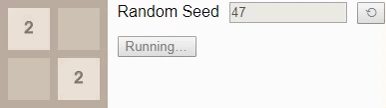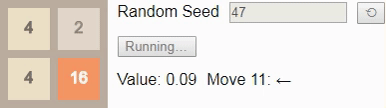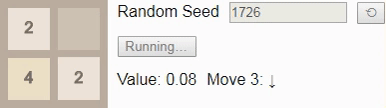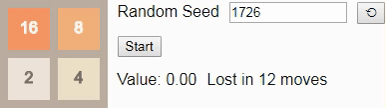
Стоит заметить, что каждый из показанных выше алгоритмов является оптимальным алгоритмом соответствующей игры, но гарантий его уникальности нет. Может быть множество аналогичных оптимальных алгоритмов, но мы с определённостью можем сказать, что ни один из них не является строго лучшим.

Если вы хотите более подробно исследовать эти модели для игры 2×2, то в Приложении А есть схемы, показывающие все возможные пути прохождения игры.

Оптимальная игра на поле 3×3
На поле 3×3 можно играть до тайла 1024, и у такой игры 25 миллионов состояний. Поэтому начертить схему MDP, которую мы делали для игр 2×2, совершенно невозможно, но мы всё равно можем понаблюдать за оптимальным алгоритмом в действии5:

Так же, как и в игре 2×2 до тайла 32, в игре 3×3 до тайла 1024 очень сложно выиграть — при оптимальной игре вероятность выигрыша всего около 1%. В качестве менее бесполезного развлечения можно выбрать игру до тайла 512, в которой вероятность выигрыша при оптимальной игре гораздо выше, примерно 74%:

Рискуя антропоморфировать большую таблицу состояний и действий, которой и является алгоритм, я вижу здесь элементы стратегий, которые я использую при игре в 2048 на поле 4×46. Мы видим, что алгоритм засовывает тайлы с высокими значениями на края и обычно в углы (хотя в игре до 1024 он часто ставит тайл 512 посередине границы поля). Также можно заметить, что он «ленив» — даже когда есть два тайла с высокими значениями, которые можно объединить, он продолжает объединять значения с меньшими значениями. Логично, что особенно в стеснённых условиях поля 3×3, стоит пользоваться возможностью увеличения суммы своих тайлов без риска (мгновенного) проигрыша — если ему не удаётся объединить меньшие тайлы, он всегда может объединить большие, что освобождает поле.

Важно заметить, что не обучали алгоритм этим стратегиям и не давали ему никаких подсказок
о том, как играть. Все его поведения и кажущийся интеллект возникают исключительно из решения задачи оптимизации с учётом переданными нами вероятностей перехода и функции вознаграждения.

Оптимальная игра на поле 4×4
Как выяснилось в предыдущем посте, игра до тайла 2048 на поле 4×4 имееет не менее триллионов состояний, поэтому пока невозможно даже перечислить все состояния, не говоря уж о решении MDP для получения оптимального алгоритма.

Однако мы можем выполнить перебор и выполнить решение для игры 4×4 до тайла 64 — в этой модели будет «всего» 40 миллиардов состояний. Как и в игре 2×2 до тайла 8, при оптимальной игре проиграть невозможно. Поэтому наблюдать за ней не очень интересно, так как во многих случаях существует несколько хороших состояний, и выбор между ними выполняется произвольным образом.

Однако если мы уменьшим коэффициент обесценивания $\gamma$ , что сделает игрока немного нетерпеливым, то он будет предпочитать выигрывать быстрее, а не позже. Тогда игра будет выглядеть немного более нацеленной. Вот оптимальный игрок при $\gamma = 0.99$ :

GIF

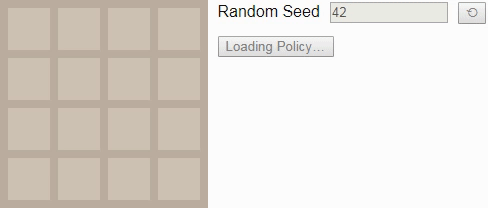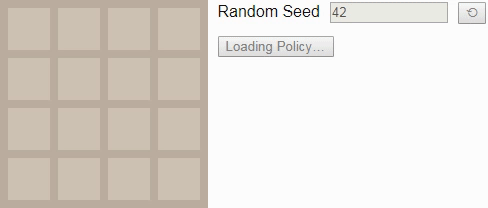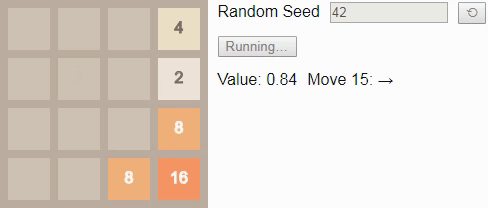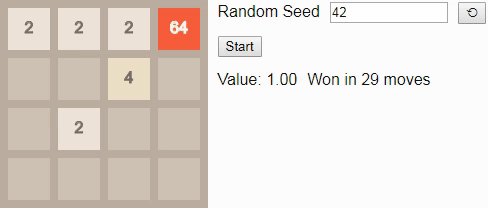
Изначально значение равно примерно 0.72; точное начальное значение отражает ожидаемое количество шагов, которые потребуются для победы из случайно выбранного начального состояния. Оно постепенно увеличивается с каждым ходом, потому что вознаграждение за достижение состояния победы становится ближе. Алгоритм снова хорошо использует границы и углы поля для построения последовательностей тайлов в удобном для объединения порядке.

Заключение

Мы разобрались, как представить игру 2048 в виде марковского процесса принятия решений и получили доказуемо оптимальные алгоритмы для игр на полях 2×2 и 3×3, а также для ограниченной игры на поле 4×4.

Использованные здесь методы требуют для решения перечисления всех состояний модели. Применение эффективных стратегий перечисления состояний и эффективных стратегий решения этой модели (см. Приложение Б) делает их пригодными для моделей, у которых до 40 миллиардов состояний, то есть для игры 4×4 до 64. Вычисления для этой модели потребовали примерно одной недели работы экземпляра OVH HG-120 с 32 ядрами, 3,1ГГц и 120ГБ ОЗУ. Следующая ближайшая игра 4×4 до тайла 128 скорее всего будет содержать во много раз больше состояний и потребует гораздо больше вычислительных мощностей. Вычисление доказуемо оптимального алгоритма для полной игры до 2048, вероятно, потребует других методов решения.

Часто выясняется, что MDP на практике слишком велики для решения, поэтому существуют проверенные техники нахождения приближенных решений. В них обычно используется хранение приблизительных функции значений и/или алгоритма, например, с помощью обучения (возможно, глубокого) нейросети. Также вместо перечисления всего пространства состояний их можно обучать на данных симуляций, используя методы обучения с подкреплением. Существование доказуемо оптимальных алгоритмов для игр меньшего размера могут сделать 2048 полезным испытательным стендом для таких методов — это может стать интересной темой для исследований в будущем.

Приложение А: канонизация

Как мы видели на примере полной модели для игры 2×2 до тайла 8, количество состояний и переходов очень быстро растёт, и становится сложно графически представить даже игры на поле 2×2.

Чтобы сохранять контроль над размером модели, мы можем снова воспользоваться наблюдением из предыдущего поста о перечислении состояний: многие из последующих состояний являются просто поворотами и отражениями друг друга. Например, состояния

и

являются просто зеркальными копиями — это просто отражения по вертикальной оси. Если лучшим действием в первом состоянии будет сдвиг влево, то лучшим действием во втором состоянии обязательно будет сдвиг вправо. То есть с точки зрения принятия решений о выборе действия достаточно выбрать одно из состояний в качестве канонического и определять наилучшее действие, которое нужно сделать из канонического состояния. Каноническое состояние заданного состояния получается нахождением всех его возможных поворотов и отражений, записью каждого как числа по основанию 12 и подбором состояния по наименьшему числу — подробности см. в предыдущем посте. Важно здесь то, что каждое каноническое состояние заменяет класс эквивалентных состояний, связанных с ним поворотом или отражением, поэтому нам не придётся иметь с ними дело по отдельности. Заменив представленные выше последующие состояния их каноническими состояниями, мы получим более компактную схему:

К сожалению, из схемы следует, что сдвиг вверх (U) из каким-то образом приведёт к . Однако парадокс разрешается, если читать стрелки и добавлять при необходимости поворот или отражение, чтобы найти действительное каноническое состояние последующего состояния.

Эквивалентные действия

Также мы можем заметить, что на показанной выше схеме на самом деле не важно, в каком направлении игрок выполнит сдвиг из состояния — канонические последующие состояния и их вероятности переходов одинаковы для всех действий. Чтобы понять, почему, стоит посмотреть на «промежуточное состояние» после того, как игрок выполнил сдвиг для перемещения тайлов, но когда игра ещё не добавила новый случайный тайл:

Промежуточные состояния отмечены пунктирными линиями. Важнее всего здесь заметить то, что все они связаны поворотом на 90°. Эти повороты не важны, если мы в результате канонизируем последующие состояния.

В более общем смысле, если два или более действий имеют одинаковое каноническое «промежуточное состояние», то у этих действий должны быть одинаковые канонические последующие состояния, а потому они эквивалентны. В показанном выше примере каноническим промежуточным состоянием оказывается последнее: .

Следовательно, мы можем ещё больше упростить схему для , если просто объединим все эквивалентные действия:

Разумеется, состояния, для которых все действия эквивалентны в таком смысле, встречаются относительно редко. Рассмотрев ещё одно потенциальное начальное состояние , мы увидим, что сдвиги влево и вправо эквивалентны, но сдвиг вверх отличается; сдвиг вниз недопустим, потому что тайлы уже находятся внизу.

Схемы моделей MDP для игр 2×2

Благодаря канонизации мы можем уменьшить модели до масштаба, при котором можно отрисовать полные MDP для некоторых небольших игр. Давайте снова начнём с наименьшей нетривиальной модели: игры 2×2 до тайла 8:

По сравнению со схемой без канонизации, эта оказалась гораздо более компактной. Мы видим, что кратчайшая возможная игра состоит всего из единственного хода: если нам повезёт начать из состояния с двумя соседними тайлами 4, что бывает только в одной игре на 150, нам достаточно всего лишь соединить их, чтобы получить тайл 8 и состояние win. С другой стороны, мы видим, что проиграть всё равно возможно: если из состояния игрок выполнит сдвиг вверх, то с вероятностью 0,9 получит , а если снова сделает сдвиг вверх, то с вероятностью 0,9 получит , и в этот момент игра будет проиграна.

Мы можем ещё сильнее упростить схему, если будем знать оптимальный алгоритм. Определение алгоритма порождает из модели MDP цепь Маркова, потому что каждое состояние имеет единственное действие или группу эквивалентных действий, определяемых алгоритмом. Порождённая цепь для игры 2×2 до 8 имеет такой вид:

Мы видим, что к состоянию lose больше не ведёт ни одно ребро, потому что при оптимальной игре в 2×2 до тайла 8 проиграть невозможно. Кроме того, каждое состояние теперь помечено своим значением, которое в этом случае всегда равно 1,000. Поскольку мы присвоили коэффициенту обесценивания $\gamma$ значение 1, то значение состояния на самом деле является вероятностью выигрыша из этого состояния при оптимальной игре.

Схемы становятся немного хаотичнее, но мы можем построить похожие модели для игры 2×2 до тайла 16:

Если мы посмотрим на оптимальный алгоритм для игры до тайла 16, то увидим, что начальные состояния (синие) имеют значения меньше единицы, и что существуют пути к состоянию lose, в частности, из двух состояний, в которых сумма тайлов равна 14:

То есть если мы будем играть в эту игру до тайла 16 оптимальным образом, то всё равно сможем проиграть, и это будет зависеть от конкретной последовательности выдаваемых нам игрой тайлов 2 и 4. Однако в большинстве случаев мы выиграем — значения в начальных состояния примерно равны 0,96, поэтому мы ожидаем выигрыша примерно в 96 играх из сотни.

Однако наши перспективы при игре до тайла 32 на поле 2×2 гораздо хуже. Вот полная модель:

Мы видим, что множество рёбер ведёт к состоянию lose, и это плохой признак. Это подтверждается, если посмотреть на схему, ограниченную оптимальной игрой:

Среднее значение для начальных состояний приблизительно равно 0.08, поэтому стоит ожидать победы примерно в 8 играх из ста. Основная причина этого становится очевидной, когда мы посмотрим на правую часть схемы: достигнув состояния с суммой 28, единственный способ победить — получить тайл 4, чтобы достичь состояния . Если мы получим тайл 2, что происходит в 90% случаев, то проиграем. Наверно, такая игра будет не очень интересной.

Приложение Б: методы решения

Для эффективного решения моделей MDP, похожих на те, что мы построили здесь для 2048, мы можем использовать важные свойства их структуры:

Модель перехода является направленным ациклическим графом (НАГ). С каждым ходом сумма тайлов должна увеличиваться, а конкретно — на 2 или на 4, то есть возврат к уже посещённому состоянию невозможен.
Более того, состояния можно упорядочить в «слои» по суммам их тайлов, как мы делали это в рисунке первой модели MDP, и все переходы будут выполняться из текущего слоя с суммой или в следующий слой с суммой , или в слой после него, с суммой .
Все состояния в слое с наибольшей суммой будут переходить в состояние проигрыша или выигрыша, которые имеют известные значения, а именно 0 или 1.

Свойство (3) означает, что мы можем пройти в цикле по всем состояниям в последнем слое, в котором известны все последующие значения, и сгенерировать функцию значений для этого последнего слоя. Далее, благодаря свойству (2), мы знаем, что состояния во втором с конца слое должны переходить или в состояния в последнем слое, для которого мы только что вычислили значения, или в состояние победы или проигрыша, которые имеют известные значения. Таким образом мы можем проделать путь назад, слой за слоем, всегда зная значения состояний в следующих двух слоях; это позволяет нам построить и функцию значений, и оптимальный алгоритм для текущего слоя.

В предыдущем посте мы выполняли работу в прямом порядке, с начальных состояний и перечисляли все состояния, слой за слоем, используя отображение-свёртку для распараллеливания работы внутри каждого слоя. Для решения мы можем использовать выходные данные этого перечисления, которые являются огромным списком состояний, чтобы выполнить работу в обратном порядке, снова применяя отображение-свёртку для параллельной работы в каждом слое. Как и в прошлый раз, мы разобьём слои на «части» по их максимальным значениям тайлов с отслеживанием дополнительной информации.

Основная реализация решателя по-прежнему довольно требовательна к памяти, потому что для обработки текущей части за один проход ей ей нужно хранить в памяти функции значений нескольких (до четырёх) частей. Можно снизить это требование до одновременного хранения в памяти всего одной части с помощью того, что обычно называется $Q^\pi(s,a)$ — значения для каждой возможной пары состояние-действие согласно алгоритму $\pi$ , а не $V^\pi(s)$ , но эта реализация решателя оказалась гораздо более медленной, поэтому все результаты получены с помощью основного решателя $V^\pi$ на машине с большим количеством ОЗУ.

В случае обоих решателей слоистая структура модели позволяет нам построить и решить модель всего одним проходом вперёд и одним проходом назад, что является значительным улучшением по сравнению с обычным методом итеративного решения. Это одна из причин, по которой мы способны решать такие достаточно большие модели MDP с миллиардами состояний. Также важными причинами являются методы канонизации из Приложения А, позволяющие снизить количество учитываемых состояний,