[Перевод] Онлайн-алгоритмы в высокочастотном трейдинге: проблемы конкуренции
Высокочастотный трейдинг [англ. High-frequency trading, HFT-trading] сегодня оказывает большое влияние на современные финансовые рынки. Еще 20 лет назад большая часть торгов проходила на биржах, к примеру, на Нью-Йоркской фондовой бирже, где люди, одетые в яркие костюмы, активно жестикулировали и выкрикивали свои предложения о покупке или продаже ценных бумаг. Сегодня торговля, как правило, осуществляется с помощью электронных серверов в дата-центрах, где компьютеры обмениваются предложениями о покупке и продаже путем передачи сообщений по сети. Этот переход от торговли в операционном здании биржи к электронным платформам был особенно выгоден HFT-компаниям, которые инвестировали много средств в необходимую для торговли инфраструктуру.
Несмотря на то, что место и участники торговли внешне сильно изменились, цель трейдеров — как электронных, так и обычных — осталась неизменной — приобрести актив у одного предприятия/трейдера и продать его другому предприятию/трейдеру по более высокой цене. Основное отличие традиционного трейдера от HFT-трейдера состоит в том, что последний может торговать быстрее и чаще, и время удержания портфеля у такого трейдера очень низкое. Одна операция стандартного HFT-алгоритма занимает долю миллисекунды, с чем не могут сравниться традиционные трейдеры, так как человек моргает примерно раз в 300 миллисекунд. По мере того, как HFT-алгоритмы конкурируют между собой, они сталкиваются с двумя проблемами:
- Каждую микросекунду они обрабатывают большой объем данных;
- Им нужно уметь очень быстро реагировать на основе этих данных, потому что прибыль, которую они могут извлечь из принимаемых ими сигналов, снижается очень быстро.
Онлайн-алгоритмы представляют собой обычный класс алгоритмов, которые можно применять в HFT-трейдинге. В таких алгоритмах новые входные переменные поступают последовательно. После обработки каждой новой входной переменной алгоритм должен принять конкретное решение, например, выставлять ли заявку на покупку/продажу. В этом и состоит главное отличие онлайн-алгоритмов от офлайн-алгоритмов, в которых считается, что все входные данные доступны в момент принятия решения. Большинство задач практической оптимизации в таких областях, как информатика и методы исследования операций — это именно онлайн-задачи [1].
Помимо решения онлайн-задач, HFT-алгоритмам также необходимо чрезвычайно быстро реагировать на рыночные изменения. Чтобы реагировать на ситуацию быстрее, трейдинговый онлайн-алгоритм должен эффективно работать с памятью. Хранение большого объема данных снижает скорость работы любого компьютера, поэтому важно, чтобы алгоритм задействовал минимальный объем данных и параметров, которые можно хранить в быстродействующей памяти, например, в кэш-памяти первого уровня (L1). Кроме того, этот набор параметров должен отражать текущее состояние рынка и обновляться по мере поступления новых переменных в режиме реального времени. Таким образом, чем меньше число параметров, которые нужно хранить в памяти, и чем меньше вычислений нужно проводить для каждого из этих параметров, тем быстрее алгоритм сможет реагировать на изменения рынка.
Учитывая требования к скорости и онлайн-природу задач HFT-трейдинга, класс однопроходных алгоритмов может с успехом применятся в HFT-трейдинге. В каждый выбранный момент времени эти алгоритмы на вход получают один элемент данных и используют его для того, чтобы обновить набор имеющихся параметров. После обновления один из элементов данных отбрасывается, и, таким образом, в памяти хранятся только обновленные параметры.
При разработке HFT-алгоритма могут возникнуть три проблемы. Первая заключается в оценке скользящего среднего ликвидности: решение этой проблемы может помочь HFT-алгоритму определить размер ордера, который, вероятнее всего, исполнится успешно на данной электронной бирже. Вторая состоит в оценке скользящей волатильности: решение этой проблемы помогает определить краткосрочный риск для той или иной позиции. Третья проблема основана на понятии линейной регрессии, которую можно применять в парном трейдинге связанных между собой активов.
Каждую из этих проблем можно без труда решить с помощью однопроходного онлайн-алгоритма. В этой статье описано, как проводилось бэк-тестирование однопроходного алгоритма на основе данных, взятых из книги лимитных ордеров для высоколиквидных биржевых инвестиционных фондов, и даны рекомендации по регулированию работы этих алгоритмов на практике.
Онлайн-алгоритмы в HFT-трейдинге
Одно из преимуществ HFT-трейдеров над другими участниками рынка заключается в скорости реакции. HFT-компании могут отследить любое движение на рынке — то есть информацию, содержащуюся в книге лимитных ордеров — и на его основе принять соответствующее решение в течение нескольких микросекунд. Хотя действия некоторых HFT-алгоритмов могут основываться на данных источника, находящегося за пределами рынка (скажем, при анализе новостных отчетов, измерении температуры или оценке рыночных тенденций), большинство принимает решения исключительно на основе сообщений, полученных непосредственно с рынка. По некоторым оценкам, котировки на Нью-Йоркской фондовой бирже обновляются примерно 215 000 раз в секунду [2]. Основная задача HFT-алгоритмов состоит в обработке полученных данных таким образом, чтобы можно было принимать верные решения, например, когда стоит выставить позицию или снизить риск. В примерах, приведенных в этой статье, учитывается, что HFT-алгоритмы могут видеть любое обновление цен лучшего бида или аска, в том числе данные об их размерах. Такой подкласс данных, содержащихся в книге лимитных ордеров, часто называют информацией из книги ордеров первого уровня (Level-1).
В этой статье подробно рассмотрены три примера онлайн-алгоримтов, каждый из которых предназначен для использования в HFT-трейдинге:
- Онлайн-алгоритм для вычисления математического ожидания. Предназначен для отыскания параметра, на основе которого можно предсказать доступную ликвидность, вычисляемую как сумма размеров лучшего бида и аска, на фиксированном отрезке времени в будущем. Определение этой величины может помочь оценить размер заявки, которая, вероятнее всего, будет исполнена по лучшей цене с учетом данной задержки.
- Онлайн-алгоритм для вычисления дисперсии. Предназначен для отыскания параметра, на основе которого можно предсказать реализованную волатильность на фиксированном отрезке времени в будущем. Определение этой величины может помочь оценить краткосрочный риск хранения запасов.
- Онлайн-алгоритм для вычисления коэффициента регрессии. Предназначен для отыскания параметра, на основе которого можно предсказать ожидаемую прибыль с удержания длинной и короткой позиций пары связанных активов. Определение этой величины может помочь при создании сигнала, который подается в случае, когда длинная и короткая позиции, вероятнее всего, принесут прибыль.
В каждом из трех случаев алгоритм содержит единственный параметр, «альфа», регулирующий скорость, с которой отбрасывается ненужная информация. На рисунке 1 синим цветом обозначено приблизительное изменение ликвидности (сумма размеров бида и аска). Красным и зеленым обозначено изменение параметра ликвидности при значениях параметра «альфа», равного 0,9 и 0,99 соответственно. Обратите внимание, что по мере приближения «альфа» к единице, уровень сигнала становится все более равномерным и точнее отражает тренд в исходных данных.
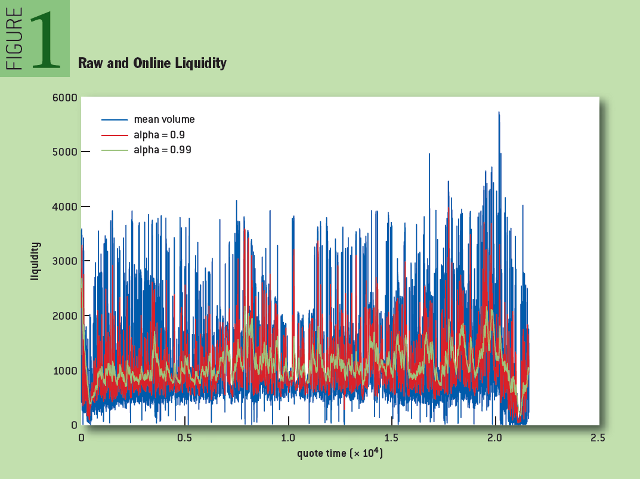
Рис. 1: Неочищенная и онлайн-ликвидность
На рисунке 2 показано изменение волатильности для разных значений параметра «альфа» в режиме реального времени. Обратите внимание, что, как и в предыдущем случае, с увеличением «альфа» кривая графика становится более гладкой. Большее значение «альфа» дает более ровный сигнал, однако высокая загруженность прошлых данных вызывает отставание от текущего тренда. Как будет показано в дальнейшем, выбор подходящего значения «альфа» будет либо давать более ровный сигнал, либо уменьшать отставание от тренда.
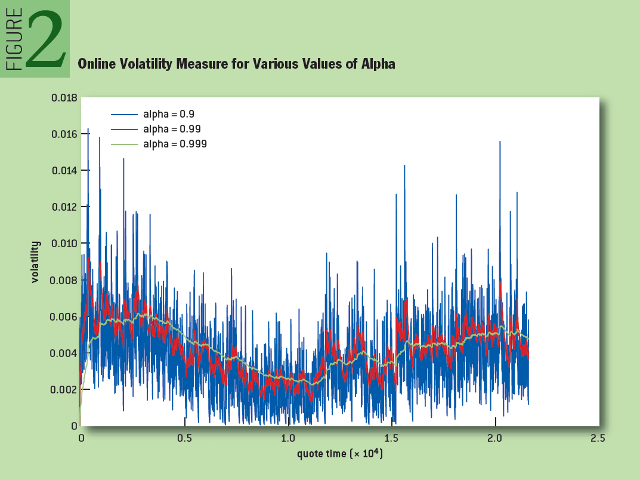
Рис. 2: Измерение онлайн-волатильности для разных значений альфа
Чтобы показать, как работает онлайн-алгоритм регрессии, мы рассмотрели временные ряды, составленные из средних цен на акции SPY и SSO — двух связанных биржевых инвестиционных фондов (SSO — тот же SPY, но объем его заемных средств вдвое больше). Как показано на рисунке 3, зависимость между двумя этими активами в процессе их изменения в течение дня близка к линейной. На рисунке 4 показано изменение математического ожидания и свободного члена для двух значений «альфа».
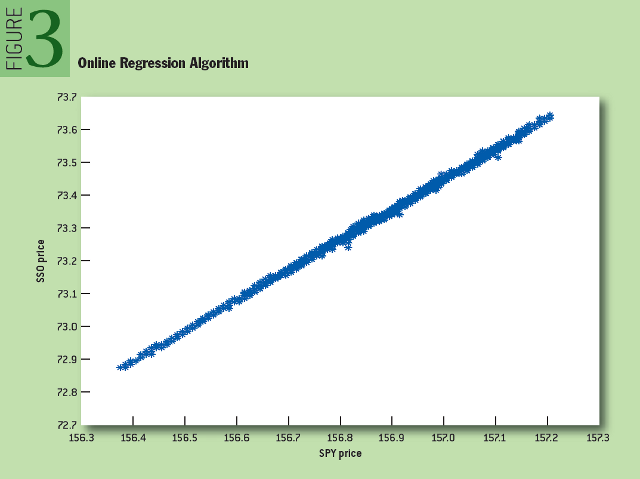
Рис. 3: Алгоритм онлайн-регрессии
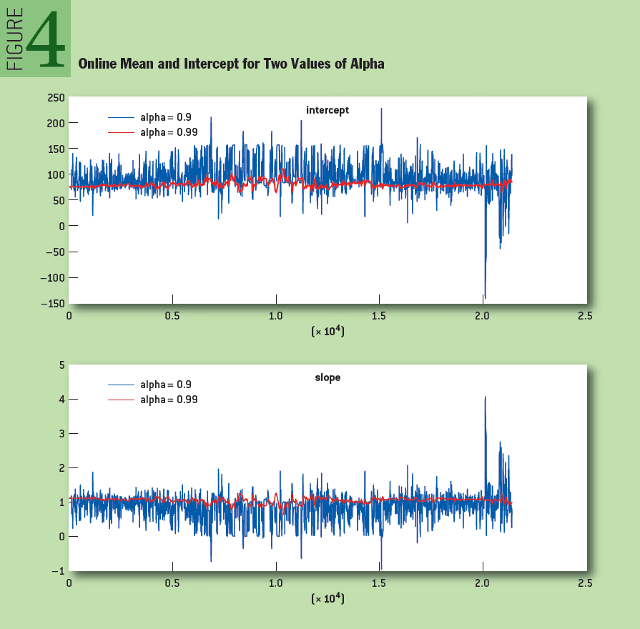
Рис. 4: Изменение математического ожидания и свободного члена для двух значений «альфа»
Однопроходные алгоритмы
Как ясно из названия, однопроходный алгоритм считывает входную переменную ровно один раз и затем отбрасывает ее. Этот тип алгоритмов эффективно распределяет память, так как он сохраняет минимальный объем данных. В данном разделе приведено три важных примера однопроходных алгоритмов: экспоненциально скользящего среднего, экспоненциально взвешенной дисперсии и экспоненциально взвешенной регрессии. В следующем разделе будет рассказано о применении этих алгоритмов в HFT-трейдинге.
Для начала кратко рассмотрим понятие простого скользящего среднего для данного временного ряда. Оно представляет собой оценку математического ожидания для временного ряда со «скользящим» окном постоянного размера. В финансовой сфере эта оценка часто используется для определения ценового тренда, в частности, при сравнении двух значений простого скользящего среднего — в случае с «длинным» окном и в случае с «коротким» окном. В качестве применения также можно рассмотреть ситуацию, когда средний объем торговли за последние пять минут помогает предсказать объем торговли в следующую минуту. В отличие от экспоненциального скользящего среднего, простое скользящее среднее нельзя определить с помощью однопроходного алгоритма.
Пусть (Xt)t = X0, X1, X2, … — это последовательность полученных входных переменных.
Для каждого отдельного момента времени t нам нужно спрогнозировать значение следующей переменной Xt+1. Для M > 0 и t ≥ M, простое скользящее среднее с окном размера M определяется как математического ожидание последних M наблюдений для временного ряда (Xt)t, то есть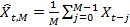 
. Скользящее среднее также можно вычислить с помощью следующей рекурсии:
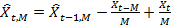. (1)
Хоть это и онлайн-алгоритм, тем не менее, он не является однопроходным, потому что каждый входной элемент ему приходится обрабатывать дважды: когда его нужно учесть при вычислении скользящего среднего и когда его нужно исключить из оценки. Такой алгоритм носит название двухпроходного алгоритма и требует хранения в памяти целого массива размера M.
Пример 1: Однопроходный алгоритм экспоненциально взвешенного среднего
В отличие от обычного среднего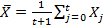 
, экспоненциально взвешенное среднее определяет экспоненциально уменьшающиеся значения весовых коэффициентов предыдущих наблюдений:
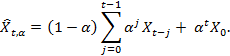
Здесь α — взвешенный параметр, который подбирается пользователем и должен удовлетворять условию 0 < α ≤ 1. В связи с тем, что для экспоненциально взвешенного среднего большую роль играют самые последние входные параметры, по сравнению с более ранними элементами данных, его часто считают достаточно точным приближением простого скользящего среднего.
В отличие от простого скользящего среднего, экспоненциально взвешенное среднее учитывает все предыдущие данные, не только последние M наблюдений. Более того, если дальше сравнивать простое скользящее среднее и экспоненциально взвешенное среднее, на рисунке 5 можно увидеть, сколько элементов данных в ходе оценки получают 80%, 90%, 95%, 99% и 99,9% весовой функции, зависящей от α. К примеру, если α = 0,95, то последние M = 90 полученных элементов данных составляют 99% оцениваемого значения. Следует отметить, что, если у временных рядов (Xt)t очень «тяжелые хвосты», то экспоненциально сглаженное среднее может состоять преимущественно из крайних наблюдений, тогда как скользящее среднее реже зависит от крайних наблюдений, так как они в итоге исключаются из окна наблюдения. Частые повторения процедуры оценки могут решить задачу долгосрочного хранения данных в памяти при экспоненциальном сглаживании.
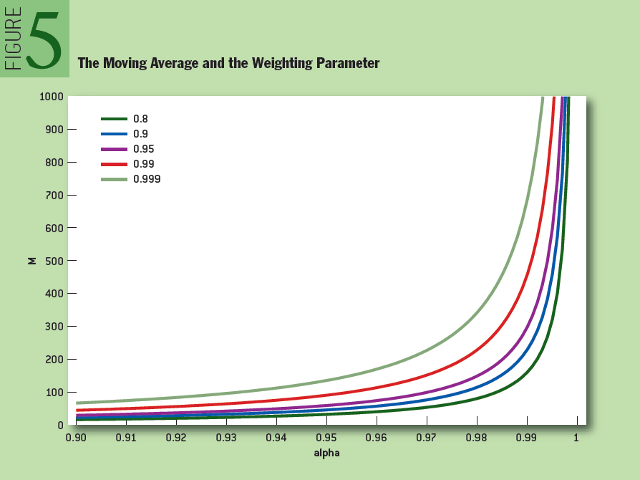
Рис. 5: Скользящая средняя и весовой параметр
Причина выбора экпоненциально скользящего среднего вместо простого скользящего среднего для использования в HFT-алгоритме состоит в том, что его можно определить с помощью однопроходного алгоритма, впервые упомянутого в работе Р.Г. Брауна (1956 г.) [3].
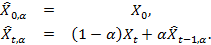. (2)
Эта формула также указывает на то, что с помощью параметра α можно регулировать весовые коэффициенты последних наблюдений, сравнивая их с предыдущими.
Пример 2: Однопроходный алгоритм экспоненциально взвешенной дисперсии
Экспоненциальное сглаживание, описанное в предыдущем разделе, позволяет оценить скользящее среднее для временных рядов. В финансах волатильность временных рядов зачастую играет немаловажную роль. Другими словами, волатильность должна отражать частоту колебаний временных рядов относительно их среднего уровня. В финансовой теории HFT-трейдинга нет однозначного определения волатильности. В этом разделе волатильность рассматривается как стандартное отклонение (квадратный корень из дисперсии) элемента данных для временных рядов (Xt)t. Так же как и в случае с экспоненциально взвешенным скользящим средним из предыдущего раздела, можно разработать однопроходный онлайн-алгоритм, который будет оценивать волатильность для временных рядов на основе схемы экспоненциально взвешенных коэффициентов.
Дисперсия случайной переменной определяется по формуле Var (X) = E[X — E[X])2]. Для того, чтобы оценить экспоненциально взвешенную дисперсию временных рядов, необходимо вначале оценить два параметра — математическое ожидание E[X] и дисперсию:
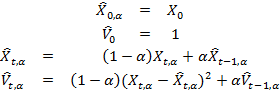
Стандартное отклонение каждой следующей контрольной точки Xt+1 оценивается как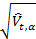 
. В этом примере входной параметр α ∈ (0,1) также подбирается пользователем и определяет значения весовых коэффициентов прошлых данных, которые сравниваются с последними из полученных входных данных. В данном случае мы принимаем начальное значение статистической оценки равным 1 — она [оценка], вообще говоря, может принимать любое значение. Другой способ — ввести пробный период, в течение которого идет наблюдение за временными рядами и в качестве первоначальной оценки использовать оценку стандартного отклонения для временных рядов в этом «тестовом» окне. Конечно, подобный метод можно также использовать и при определении оценки экспоненциально взвешенного среднего.
Пример 3: Однопроходный алгоритм экспоненциально взвешенной линейной регрессии
Последним примером является однопроходный онлайн-алгоритм на основе модели экспоненциально взвешенной линейной регрессии. Эта модель похожа на модель обычной линейной регрессии, но в отличие от нее она акцентирует больше внимания (в соответствии с экспоненциальным взвешиванием) на последние наблюдения, чем на более ранние. Как уже было показано, такие методы регрессии играют важную роль в HFT-стратегиях и помогают определить связь между различными активами, их, в частности, можно использовать в стратегиях парного трейдинга.
В нашей модели мы рассматриваем двумерные временные ряды (Xt, Yt)t и предполагаем, что переменные X и Y связаны линейным соотношением, в которое входит и случайная погрешность εt с нулевым математическим ожиданием, то есть:
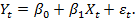. (3)
Переменную Y называют переменной отклика, а переменную X — объясняющей переменной. Для простоты предположим, что у нас имеется одна объясняющая переменная, хотя обобщение до нескольких объясняющих переменных провести не так сложно. При стандартном подходе к определению линейной регрессии с помощью офлайн-алгоритма параметры β0 и β1 подбираются уже после всех наблюдений. Элементы данных каждого отдельного наблюдения записываются в отдельный вектор Y = (Y0, Y1, …, Yt)T или матрицу
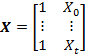
Столбец из единиц в матрице X соответствует свободному члену в уравнении 3. Если мы запишем параметры β0 и β1 в виде вектора β = (β0, β1)T, то соотношение между Y и X можно компактно записать в матричной форме:
Y = Xβ + ε
где ε — это вектор стохастических погрешностей, каждая из которых имеет нулевое математическое ожидание.
Самый распространенный подход к оценке параметра β заключается в использовании стандартного метода наименьших квадратов, то есть β выбирается таким образом, чтобы сумма квадратов остаточных членов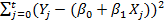 
была минимальной. Решением данной задачи минимизации будет 
.
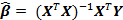Как и при оценке математического ожидания и дисперсии, при оценке параметра β большую роль должны играть более поздние наблюдения. Кроме того, однопроходный алгоритм для поиска значений β необходим для проведения вычислений.
Далее, рассмотрим рекурсивный метод, последовательно обновляющий значения вектора β и минимизирующий выражение:
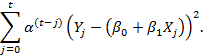
Напомним, что параметр должен находиться на интервале (0,1) и выбираться пользователем. Параметры β0 иβ1 оценки по методу взвешенных наименьших квадратов можно вычислить с помощью эффективного однопроходного онлайн-алгоритма. На каждом шаге алгоритма матрица Mt размерности 2 × 2 и вектор Vt размерности 2 × 1 должны сохраняться в памяти и обновляться по мере получения новых данных в соответствии со следующими рекурсивными выражениями:
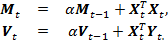
Что касается оценки математического ожидания и дисперсии, то для них инициализацию переменных рекурсии можно провести в пробном периоде. В итоге к моменту времени t лучшая оценка β будет вычисляться по формуле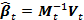 
. В литературе этот метод носит название рекурсивного метода наименьших квадратов с экспоненциальным забыванием [2].
Оценка параметра «альфа»
Как определить оптимальное значение «альфа», единственного параметра, используемого в каждой из вышеупомянутых моделей онлайн-алгоритмов? Наш подход в каждой из трех моделей заключался в определении функции отклика, значение которой мы хотим предсказать, и минимизации квадрата разности между откликом ri и нашим параметром fi:
Этот метод позволяет определить оптимальное значение «альфа» на основе исторических временных рядов. Другой подход состоит в оценке оптимального значения «альфа», которая проводится также в режиме реального времени. Однако он требует большего объема работы и выходит за рамки темы данной статьи.
Теперь рассмотрим подробнее описанные оценки онлайн-алгоритмов и оценим оптимальное значение «альфа» на конкретном множестве данных.
1. Оценка средней ликвидности вычисляется по формуле:
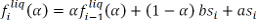
где индекс i обозначает момент времени, когда была выставлена котировка. Функция отклика определяется как ликвидность, которая наблюдается спустя десять секунд:
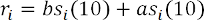
где слагаемое bsi (10) представляет собой размер бида спустя десять секунд после выставления i-й котировки. После проведения оптимизации по параметру «альфа» было показано, что оптимальное значение «альфа» для наших данных составляет 0,97. Оно представлено на рисунке 6 в виде диаграммы рассеяния для искомого параметра и функции отклика:
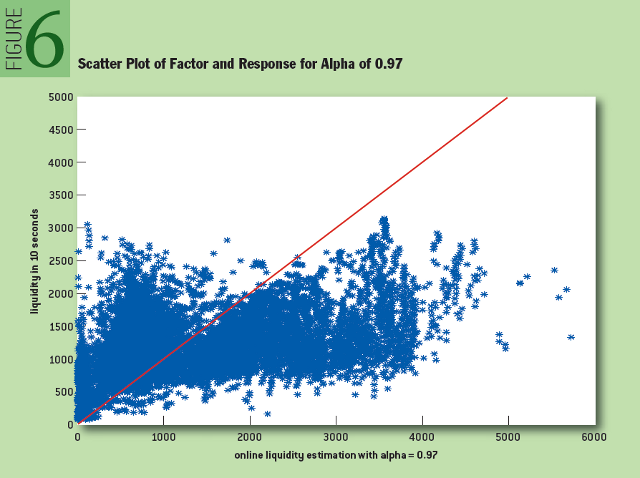
Рис. 6: Диаграмма рассеяния для искомого параметра и функция отклика для значения «альфа» 0,97
2. Оценка волатильности определяется по формулам:
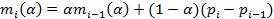
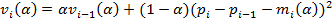
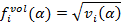
где индекс i обозначает текущее время в секундах. Величина отклика определяется как реализованная волатильность за последнюю минуту:
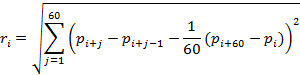
Как и в предыдущем случае, в результате перебора значений параметра «альфа» оптимальным для нашего набора данных оказалось значение, равное 0,985. На рисунке 7 показана диаграмма рассеяния для искомого параметра и функции отклика:
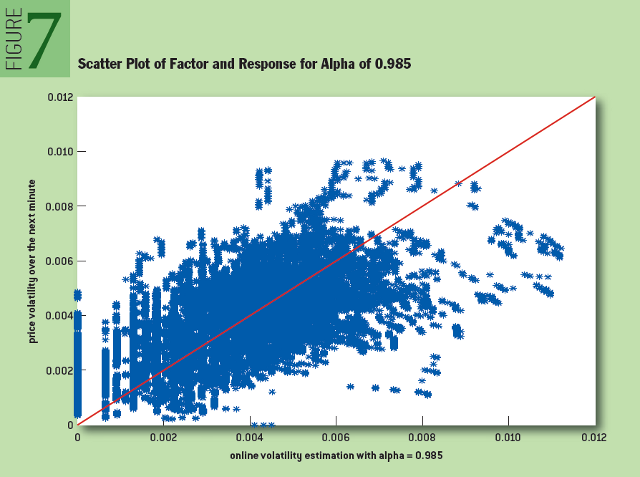
Рис. 7: Диаграмма рассеяния и функция отклика для «альфа» 0,985
3. Оценка регрессии при парном трейдинге находится по формулам:
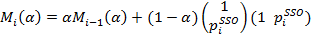
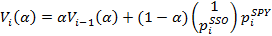
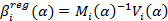
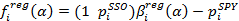
где индекс i обозначает момент времени, когда была выставлена котировка. Параметр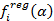 
обозначет ценность акций SPY по сравнению с акциями SSO, то есть, если их разница положительна, то акции SPY относительно дешевле, и удержание длинной позиции на SPY, вероятнее всего, окажется прибыльным.
Функция отклика определяется как прибыль, полученная за последнюю минуту со сделки, которая состоит из удержания длинной позиции на одну акцию SPY и короткой позиции на β акций SSO:
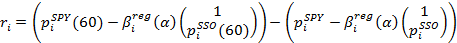
где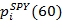 
представляет собой стоимость акции SPY спустя 60 секунд после выставления стоимости 
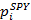. Отклик ri указывает на прибыльность следующей стратегии на удержание длинной и короткой позииций: «Купить одну акцию SPY и продать β акций SSO в момент времени i, по истечении 60 секунд закрыть позицию».
На изученном множестве данных оптимальным оказалось значение «альфа», равное 0,996. На рисунке 8 показана диаграмма рассеяния для искомого параметра и функции отклика:
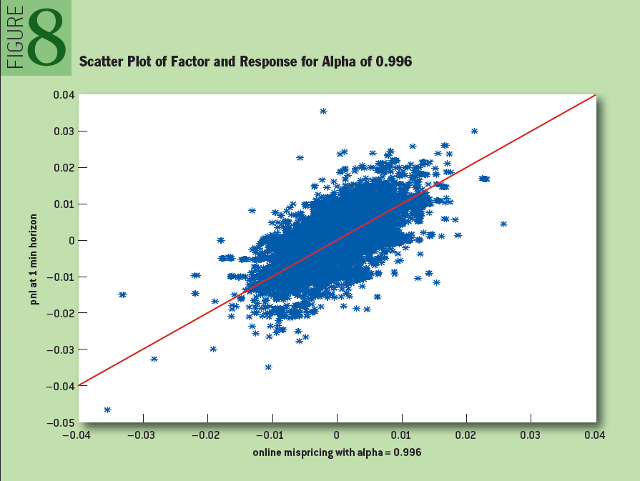
Рис. 8: Диаграмма рассения и функция отклика для «альфа» 0,996
Заключение
Однопроходные онлайн-алгоритмы являются эффективным инструментом в HFT-трейдинге, где каждую микросекунду им приходится обрабатывать большие объемы данных и очень быстро принимать решения на их основе. В этой статье были рассмотрены три проблемы, с которыми сталкиваются HFT-алгоритмы: оценка скользящего среднего ликвидности, необходимая для определения размера ордера, который, вероятнее всего, будет исполнен успешно на конкретной электронной бирже; оценка скользящей волатильности, необходимая для вычисления краткосрочного риска той или иной сделки; скользящая линейная регрессия, которая может применяться в парной торговле связанных активов. Однопроходные онлайн-алгоритмы могут сыграть ключевую роль в решении этих проблем.
Другим важным фактором для HFT-торговцев, о котором мы часто пишем в блоге на Хабре, является скорость работы. Одной из часто использующихся технологий повышения скорости получения и обработки данных является прямой доступ к бирже, который организуется с помощью различных протоколов передачи финансовой информации. Мы рассматривали технологию прямого доступа в этой статье, а о протоколах передачи данных писали здесь (раз, два, три).
Примечания:
- Албрес С. 2003. Онлайн-алгоритмы: анализ. Математическое программирование 97(1–2): 3–26.
- Кларк К. 2011. Улучшение скорости и прозрачности рыночных данных. Биржи. whatheheckaboom.wordpress.com/2013/10/20/acm-articles-on-hft-technology-and-algorithms, www.utpplan.com .
- Браун Р. Г. 1956. Экспоненциальное сглаживание для прогнозирования спроса. Arthur D. Little Inc., с. 15.
- Астром А., Уиттенмарк Б. 1994. Адаптивное управление, второе издание. Addison Wesley.
Об авторах:
Джейкоб Лавлесс (Jacob Loveless) — исполнительный директор Lucera и бывший руководитель отдела высокочастотной торговли в Cantor Fitzgerald. За последние десять лет господин Лавлесс успел попробовать себя в электронной торговле практически каждым из активов в различных HFT-компаниях и на различных биржах. До начала карьеры в финансовой сфере господин Лавлесс находился на должности особого подрядчика Министерства обороны США, где специализировался на эвристическом анализе секретных данных. До этого он также являлся главным техническим директором (CTO) и основателем Data Scientific. Основоположник анализа распределенных систем.
Саша Стойков (Sasha Stoikov) — старший научный сотрудник школы Cornell Financial Engineering Manhattan (CFEM) и бывший вице-президент отдела высокочастотной торговли в Cantor Fitzgerald. Он работал консультантом в Galleon Group и Morgan Stanley, а также читал лекции в институте им. Куранта при Нью-Йоркском университете и на кафедре организации производства и исследования операций в Колумбийском университете. Он получил степень Ph.D. в Техасском университете и степень бакалавра в Массачусетском технологическом институте.
Рольф Вайбер (Rolf Waeber) — специалист по количественному анализу в Lucera, в прошлом занимался количественными исследованиями в отделе высокочастотного трейдинга Cantor Fitzgerald. Он принимал участие в исследованиях регулирования риска ликвидности в рамках разработки документов «Базель II/III» в Немецком федеральном банке. В 2013 году Рольф получил степень Ph.D в области исследования операций и информационной инженерии Корнельского университета. Кроме того, он получил степени бакалавра и магистра математики в высшей технической школе Цюриха, Швейцария.
