[Перевод] Обучение с подкреплением: сети Deep Q21.06.2022 11:46

В предыдущих материалах из этой серии мы рассказали о том,  что такое обучение с подкреплением (Reinforcement learning, RL), поговорили о том, почему это важно, разобрались с математическим аппаратом, используемым для создания RL-агентов.

Напомним, что цель RL-алгоритма заключается в том, чтобы найти такие правила поведения , которые позволяют достичь максимальных ожидаемых результатов в окружающей среде, в которой работает алгоритм.

Мы знаем о том, что RL-алгоритмы должны максимизировать ожидаемые результаты, но к какой именно цели им нужно стремиться, что именно им нужно оптимизировать? В обычной задаче машинного обучения, вроде задачи регрессии, модель можно оптимизировать, минимизируя среднеквадратичную ошибку (Mean Squared Error, MSE). Нейронная сеть, минимизирующая MSE, будет всё лучше и лучше предсказывать целевые значения, выраженные непрерывными величинами, делая это на основе предлагаемых ей входных данных. Можно ли найти похожее понятие «ошибки», такой, минимизация которой приведёт к тому, что агент максимизирует результаты?

Да — это возможно. Для этого мы воспользуемся Q-функциями. Q-функция — это лишь одно из названий ожидаемых результатов — , а цель агента заключается в том, чтобы достичь maxQs, a. Q-функции ещё известны как функции ценности действия (action-value functions), так как они прогнозируют то, какой результат может получить агент, если совершит конкретное действие. Если представить, что Q-функции умеют разговаривать, то окажется, что рассуждают они так: «Если я совершу действие , то, думаю, получу результат ».

Ниже мы выведем алгоритм Q-обучения и продемонстрируем то, как его применение привело к одному из первых важных открытий, ставших основой сферы глубокого обучения с подкреплением. Речь идёт о сетях Deep Q (Deep Q Network, DQN). DQN были первыми AI-агентами, способными успешно играть в видеоигры, получая на вход изображения игрового экрана. Ниже показано, как DQN-агент играет в классическую игру Breakout.

DQN-агент играет в Atari Breakout

Уравнение Беллмана

Мы до сих пор не знаем о том, как Q-функция превращается цель обучения для RL-алгоритма. Но мы уже близки к ответу на этот вопрос. Сделав несколько наблюдений, мы можем вывести функцию потерь для алгоритма обучения с подкреплением. Основываясь на определении — , где  — это коэффициент дисконтирования, мы можем переписать Q-функцию с использованием рекурсивного отношения. В следующей записи  — это флаг готовности, который принимает значение false для каждого шага эпизода за исключением последнего. На этом шаге эпизод завершается, а флаг устанавливается в true.

Три шага, ведущих от Q-функции к уравнению Беллмана: 1 — рекурсивное разложение Q, 2 — отбрасывание последнего значения Q, 3 — оптимальное значение Q

На шаге (1) мы выполняем разложение суммы в определении Q. На шаге (2) нам нужен член , так как на последнем шаге эпизода Q-функция равна последнему вознаграждению (после этого никаких вознаграждений уже не будет). На шаге (3) мы отметили, что оптимальное значение Q,  , достигается путём выбора действия, которое даст наивысшие результаты. Это — то, что называется уравнением Беллмана.

От этого уравнения несложно перейти к цели оптимизации. Если нам нужно максимизировать Q — значит — надо обеспечить то, чтобы левая и правая части уравнения Беллмана были бы равны друг другу. Поэтому для обучения RL-алгоритма нужно минимизировать среднеквадратичную ошибку — так же, как это делается в задаче регрессии!

Цель оптимизации при Q-обучении — минимизация ошибки Беллмана

Эту ошибку называют ошибкой Беллмана.

Сети Deep Q

Если пространства состояния и действия дискретны и малы, тогда — это всего лишь таблица, строки которой представляют состояния, а столбцы — действия. Модель может изучить табличную Q-функцию, беря каждое состояние и действие и рекурсивно обновляя значения Q. Но представим, что нам нужно управлять беспилотным транспортным средством, используя входные данные, представленные изображением. Если так — тогда пространство состояния оказывается просто огромным (это — количество возможных изображений), а значит — мы больше не можем хранить Q в виде таблицы.

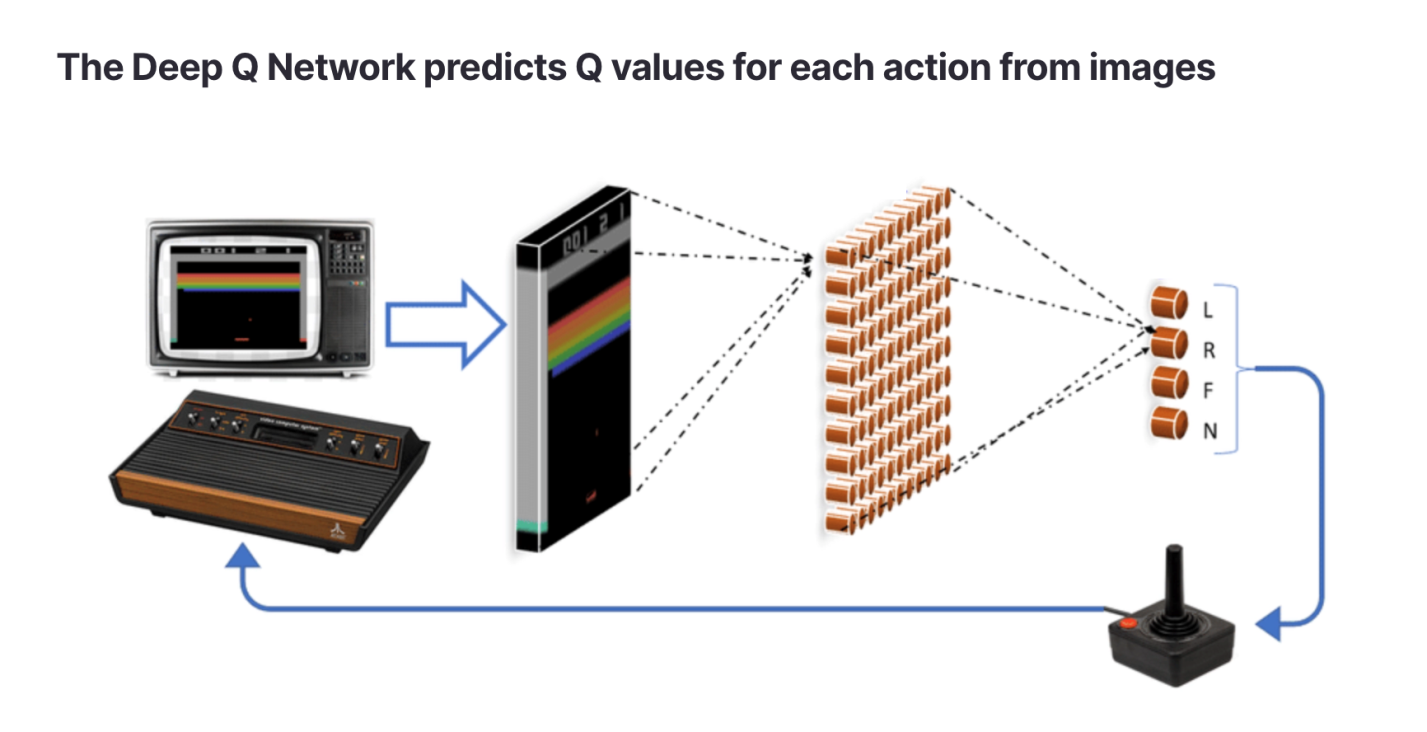Сеть Deep Q прогнозирует значения Q для каждого действия на основе изображений Источник: https://arxiv.org/abs/1903.11012

Q-сеть

Если написать псевдокод, похожий на Lua-код, в котором используется библиотека Torch, то многослойный перцептрон (Multi-Layer Perceptron, MLP), представляющий Q-сеть, будет выглядеть так:

"""
Сеть для прогнозирования значений Q
"""
class Qnet:
def init(self, action_dim, state_dim, hidden_dim):
# простой MLP, выводящий значения Q для каждого действия
self.net = nn.Sequential([nn.Linear(state_dim, hidden_dim), nn.ReLU(), nn.Linear(hidden_dim, hidden_dim), nn.ReLU(), nn.Linear(hidden_dim, action_dim)])
def forward(self, x):
return self.net(x)

Вычисление ошибки Беллмана

Для обработки входных данных, представленных изображениями, вроде тех, что поступают от игр Atari, можно воспользоваться не многослойным перцептроном, а свёрточной нейронной сетью. Но в этом примере мы, ради простоты, остановимся на MLP. Ошибку Беллмана можно вычислить так:

"""
Вычисление ошибки Беллмана с учётом данных о переходе между состояниями (s, a, r, s_next, d)
"""
def BellmanError(network, s, a, r, s_next, d, gamma):
прогнозируем Q для всех действий из состояния (s)
all_Q = network(s)
извлекаем только значения Q для выполненных действий (a)
Q = all_Q[a]
вычисляем целевые значения Q для следующего состояния (s_next)
all_target_Q = network(s_next)
берём самые большие значения Q
target_Q = argmax(all_target_Q, dim=1)
Правая часть уравнения Беллмана
rhs = r + gamma*(1-d)*target_Q
вычисляем среднеквадратичную ошибку Беллмана
return mean((Q - rhs)**2)

Буфер примеров

Мы, на псевдокоде, реализовали Q-сеть и функцию вычисления ошибки Беллмана. А откуда берутся данные о переходах между состояниями — (s, a, r, s_next, d)? В процессе обучения модели агент действует в окружающей среде и хранит все переходы, выполняемые им, в базе данных, называемой буфером примеров (replay buffer). Для вычисления ошибки Беллмана мы равномерно выбираем данные из буфера — так же, как мы бы делали это в ходе обычного обучения с учителем:

s, a, r, s_next, d = random_transitions_from_buffer(replay_buffer)

Эпсилон-жадный метод исследования среды

И наконец — нам нужно указать то, как агент выбирает действия при обучении. Оптимальной стратегией тут был бы выбор (в каждом состоянии) действия с самым высоким значением Q. Но это привело бы к ограничению возможностей агента по исследованию среды, так как агент всегда выбирал бы лишь локально-оптимальные действия, даже в том случае, если исследование среды могло бы привести его к областям, способным дать более высокое вознаграждение. Тут речь идёт о задаче исследования окружающей среды в обучении с подкреплением, о которой мы уже говорили. Для того чтобы обеспечить исследование окружающей среды, а не только выбор локально-оптимальных действий, можно решить, что иногда агент будет выполнять случайные действия, а иногда — оптимальные. Эта стратегия известна как эпсилон-жадный метод исследования среды (epsilon greedy exploration):

def epsilon_greedy_step(state, epsilon, action_dim, network):
if uniform(0,1) < epsilon:
# случайное действие
return randint(action_dim)
else:
# "жадное” действие
return argmax(network(state))

Итоги

Мы рассказали о Q-обучении и о DQN. Гораздо более масштабный вариант нашей простой модели был использован в 2013 году, в знаменитой системе, которая играла в игры Atari и стала катализатором развития сферы глубокого обучения с подкреплением. Другие алгоритмы, которые в наши дни прокладывают дорогу к практическому применению, вроде SlateQ для рекомендательных систем, это — преемники простой идеи организации Q-обучения путём минимизации ошибки Беллмана.

В следующем материале из этой серии вы найдёте практические рекомендации по обучению DQN.

О, а приходите к нам работать?

© Habrahabr.ru