[Перевод] Наследие Якоба Бернулли в Wolfram Language (Mathematica)
Перевод поста Олександра Павлыка (Oleksandr Pavlyk), «Jacob Bernoulli«s Legacy in Mathematica».Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, а также дополнительные материалы, можно здесь.16 января 2015 г. исполнилось 360 лет со дня рождения Якоба Бернулли.
In[1]:=
Out[2]=
In[3]:=
Out[3]=
In[4]:=
Out[4]=
Якоб Бернулли стал первым математиком известнейшей семьи Бернулли, к которой принадлежат многие известные математики XVII и XVIII веков.
Математическое наследие Якоба Бернулли очень богато. Он ввел так называемые числа Бернулли (Wiki / MathWorld), нашел решение дифференциального уравнения Бернулли (Wiki / MathWorld), изучал процесс Бернулли (Wiki / MathWorld), доказал неравенство Бернулли (Wiki / MathWorld), вычислил число e (Wiki / MathWorld), а также выявил слабый закон больших чисел (теорема Бернулли) (Wiki / MathWorld).In[5]:=
Out[5]=
Трактат Бернулли Ars Conjectandi (The Art of Conjecturing — Исскусство предположения) был посмертно опубликован в 1713 г., спустя 8 лет после его кончины, он был написан на латыни, лингва франка своего времени. Она рассматривается как основополагающая работа по теории вероятностей. О ее важности свидетельствует, в частности, то, что она была переведена на французский G. Le Roy в 1801 г. и, недавно, на английский E.D. Sylla в 2005 г.
Ars Conjectandi состоит из 4 частей. Первая часть воспроизводит работу Христиана Гюйгенса De Ratiociniis in Ludo Aleae. (On Reasoning in Games of Chance — О расчётах в азартной игре) с обширными комментариями от Бернулли и подробными решениями пяти проблем Гюйгенса, поставленных в конце работы Гюйгенса с указанием ответов, но без доказательств. В первой части Бернулли также выводит вероятность того, что среди n независимых испытаний будет по крайней мере m успешных, если вероятность успеха в каждом испытании равна p:
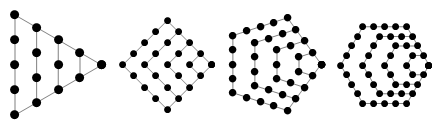
Вторая часть «The Doctrine of Permutations and Combinations» (Учение о перестановках и комбинациях) посвящена комбинаторике и изучению фигурных чисел (Wiki / MathWorld), т. е. чисел, которые могут быть представлены в виде набора точек, расположенных на плоскости в форме правильных геометрических фигур:
Именно в этой части Бернулли ввел так называемые числа Бернулли. Он начал с того, что выявил соотношение для биномиальных коэффициентов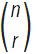 
, которое имеет вид:
.
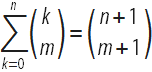In[6]:=
Out[6]=
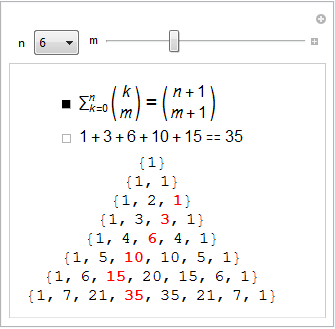
Бернулли знал, что для фиксированного значения числа m, биномиальный коэффициент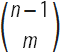 
представляет собой полином от переменной n, а именно 
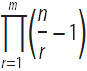. Это тождество позволило ему вывести значения сумм степеней натуральных чисел 
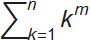. Он получил таблицу результатов для 0≤m≤10.
Для того, чтобы воспроизвести таблицу, полученную Бернулли, создадим функцию, задающую уравнения для сумм степеней натуральных чисел:
In[7]:=
In[8]:=
Out[8]=
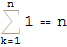
In[9]:=
Out[9]=
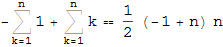
In[10]:=
Out[10]=
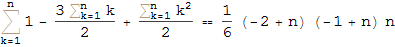
Решая полученную систему уравнений, получим:
In[11]:=
Out[11]=
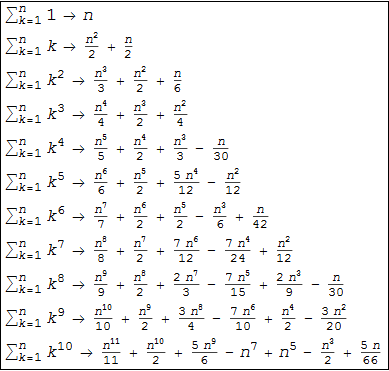
Бернулли писал, что «Тот, кто внимательно изучил полученную последовательность, может продолжить Таблицу далее без каких либо дополнительных вычислений», заметив, что:
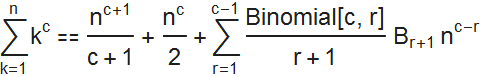
Он отметил, что коэффициенты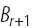 
не зависят от n, и могут быть вычислены рекурсивно, если подставить n==1 в уравнение выше.
In[12]:=
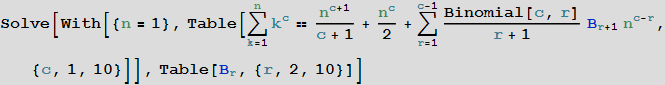
Out[12]=
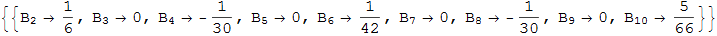
Эти коэффициенты и есть известные числа Бернулли, которые нашли свое применение во множестве областей математики [например, см. обсуждение Why do Bernoulli numbers arise everywhere? (Почему числа Бернулли появляются повсюду?) на сайте mathoverflow.net]:
In[13]:=
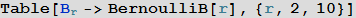
Out[13]=
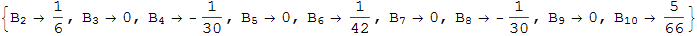
Во второй части своей книги Бернулли вычисляет число возможных перестановок, число перестановок в множестве с повторяющимися элементами, число способов выбора заданных объектов из множества и т. д., которые он позже применяет для вычисления вероятности, как отношения числа благоприятных событий к общему возможному числу событий.
В третьей части Бернулли применяет результаты, полученные в предыдущих двух частях к решению 24-х проблем, связанных с азартными играми. Лейтмотивом всех этих задач является последовательность независимых результатов 0 и 1, которая получила название «процесса Бернулли». Думаю, что 360-летие со дня рождения Якоба Бернулли является отличным поводом для того, чтобы решить его задачи в Mathematica с помощью Wolfram Language.
Например, в задаче 9 требуется найти ожидаемый выигрыш в игре трех игроков. Игроки поочередно берут карты (без замены и возвращения) из колоды в 20 карт, при этом 10 из них фигурные. Когда карты заканчиваются, выигрыш распределяется поровну среди тех игроков, у которых фигурных карт оказалось больше.
Положим, что c1, c2, и c3 — число фигурных карт у каждого игрока, тогда доля выигрыша первого игрока будет равна:
In[14]:=
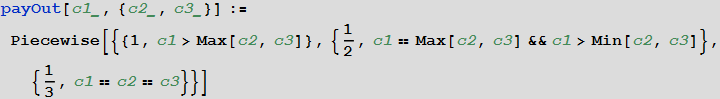
Предположи, что после того, как колода из 20 карт была таким образом распределена между игроками, получилось так, что первый и второй имеют по 7 карт, а третий — 6. Итоговый вектор распределения фигурных карт между игроками имеет многомерное гипергеометрическое распределение, которое задается в языке Wolfram Language функцией MultivariateHypergeometricDistribution:
In[15]:=
In[16]:=
Out[16]=
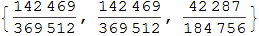
In[17]:=
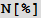
Out[17]=
Эта и другие задачи рассмотрены и решены в приложенном документе (на англ. языке).
В заключительной части трактата Ars Conjectandi обсуждается использование теории вероятностей в решении гражданских, нравственных и экономических вопросов. В этой части Бернулли утверждает, что теория вероятностей отражает наше неполное знание о состоянии мира, и, в отличие азартной игры, где вероятность может быть определена путем нахождения отношения числа благоприятных исходов некоторого опыта к их общему возможному числу, вероятность в «реальной» жизни не может быть априори установлена. Бернулли утверждает, что эти неизвестные вероятности могут быть вычислены на основе результатов, наблюдавшихся в прошлом.
Он доказал слабый закон больших чисел, который утверждает, что наблюдаемая частота успехов в серии из n независимых испытаний, вероятность успеха в каждом из которых равна p, будет неограниченно приближаться к p с неограниченным увеличением количества испытаний. Таким образом, мы можем оценить вероятность с произвольной точностью, взяв достаточное количество испытаний. Таким образом, для любых δ и ε, найдется такое число n (количество испытаний), что
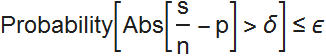
In[18]:=
Out[18]=
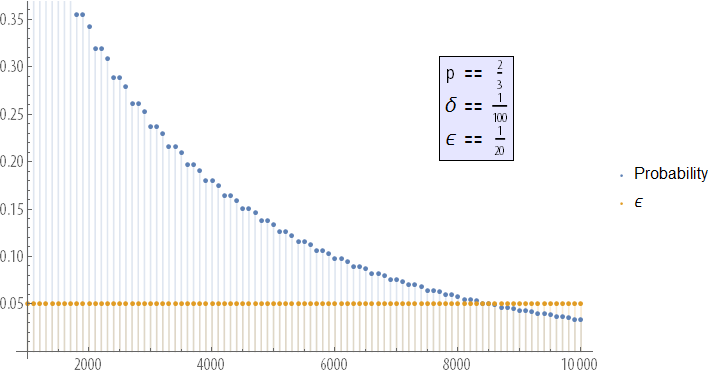
Демонстрация «Имитация эксперимента по подбрасыванию монеты и закон больших чисел» (Simulated Coin Tossing Experiments and the Law of Large Numbers), созданная Яном Маклеодом (Ian McLeod) для сайта Wolfram Demonstrations Project, в частности, демонстрирует этот процесс сходимости.
