[Перевод] Модель взаимодействия судов с водой в видеоиграх

Давайте поговорим о физике транспортных средств
Физика транспортных средств в видеоиграх не очень сильно обсуждается. Статьи в Интернете о физике транспорта в видеоиграх немногочисленны и поверхностны; обычно они посвящены самым основам. Программист транспорта для видеоигр ощущает себя сегодня в относительном вакууме. Возможно, такая ситуация возникла, потому что эту тему довольно сложно объяснить, а может быть, мы просто стыдимся признаваться в использовании хаков, упрощений и хитростей, которые мы вносим по сравнению с «правильной», реалистичной симуляцией физики. Как бы ни обстояло дело, видеоигры имеют уникальные проблемы в симуляции транспорта, а значит, об этом стоит писать. Это захватывающая тема, относящаяся к физике, работе с камерой, звуку, спецэффектам, а также к восприятию и психологии человека.
Я решил сначала поговорить о судах, потому что недавно работал с ними; ещё я обнаружил, что их динамика не совсем понимается даже на уровне исследований (хотя многое и понятно). Модели и теории формулируются таким образом, что их становится сложно применить непосредственно в видеоиграх. Или же они требуют очень ресурсоёмких методов симуляции, которые практически невозможно контролировать и адаптировать под причудливые потребности разработчиков и игроков. Но можно написать упрощённую модель, которая учитывает важные параметры судна. В этом определённо есть доля искусства, «прыжка веры» и небольшая доля «творческой» физики, которая заставит Кельвина и Стокса перевернуться в могилах.
Серия статей о физике судов
В этой серии я представлю алгоритм расчёта самых важных сил, действующих на судно в воде. Прежде всего я стремлюсь к созданию модели, описывающей основные динамические особенности поведения судов на воде, не обращаясь при этом с сложному и ресурсоёмкому расчёту динамики жидкости.
Я ограничу себя разумными затратами производительности, например, менее 1 мс на одно судно. Модель должна быть достаточно универсальной, чтобы симулировать поведение судов различных размеров и форм в условиях от штиля до шторма.
В первой статье из этой серии мы будем работать с гидростатическими силами, а также заложим важный фундамент для расчёта всех других сил, задействованных в модели. Другими силами являются динамические силы, возникающие вследствие движения судна относительно воды. Они будут рассмотрены в следующих статьях.
Знакомство с выталкивающей силой
Прежде чем углубиться в сам алгоритм, я хочу немного поговорить от выталкивании. Всё, что нам достаточно будет сделать — рассчитать величину и точку приложения выталкивающей силы к телу, частично погружённому в жидкость.
Когда тело погружено в жидкость, вследствие давления жидкости она прилагает к поверхности тела силу. Чем больше давление, тем больше сила. Сила является результатом движения множества частиц воды в жидкости, упруго ударяющихся о поверхность тела (наподобие идеальных биллиардных шаров). Это микроскопическая сила, воздействие которой ощущается даже если вода не движется в каком-то определённом направлении (течение) и если судно остаётся неподвижным; поэтому она называется гидростатической силой. Суммарная сила всех этих атомов или молекул, ударяющихся о поверхность, перпендикулярна поверхности. Следует также упомянуть, что давление в воде увеличивается на глубине (на планете с гравитацией), поскольку бОльшая глубина подразумевает, что всё больше и больше воды давит вниз своим весом. Однако давление само по себе не имеет определённого направления, и даже если непосредственно над какой-то точкой воды нет жидкости, давление в этой точке всё равно будет зависеть от общей глубины поблизости. (*)

Увеличение силы при погружении очень важно для выталкивания, поскольку результирующая выталкивающая сила возникает вследствие дисбаланса вертикальной составляющей гидростатических сил на поверхность тела. Горизонтальная составляющая гидростатических сил всегда уравновешивается. Это понятно интуитивно — для каждой отдельной элементарной площадки (замкнутого) объёма всегда можно на той же глубине найти элементарную площадку, направленную в противоположном направлении. Поскольку значения гидростатических сил одинаковы, но направлены в противоположные стороны, они уравновешиваются. С другой стороны, вертикальная составляющая гидростатических сил не уравновешивается. В общем случае, поскольку объём замкнут, поверхности, нормали которых направлены вниз, обычно находятся на большей глубине, чем поверхности, нормали которых направлены вверх. Поэтому силы давления, действующие на поверхности с направленными вниз нормалями, преобладают. Сила давления действует в направлении, противоположном нормалям, результирующая сила направлена вверх и можно доказать [2], что её значение равно «весу вытесненной жидкости» (весу объёма тела, заполненного водой).
У нас всё ещё не хватает одного кусочка пазла: чтобы всё вышеуказанное приводило к выталкиванию, нам также нужно указать точку приложения гидростатической силы. Точкой приложения выталкивающей силы является точка, относительно которой моменты всех гидростатических сил уравновешиваются. Если мы продолжим рассуждения на основании элементарных площадок погружённого тела, всё станет немного менее очевидным. Поскольку гидростатические силы увеличиваются при большем погружении, точка приложения гидростатической силы на заданную горизонтальную поверхность в общем случае находится ниже, чем центр поверхности. Как показано в Приложении A на примере погружённого треугольника (это удобный пример, потому что в играх объекты обычно состоят из треугольников), точка приложения силы всегда ниже центра. Несмотря на то, что сумма всех моментов всех приложенных сил обычно ниже центра любой поверхности, всё равно уравновешивается рядом с центром тяжести объёма. Формальное доказательство этого приведено в [2] с использованием теоремы Остроградского-Гаусса (**), или теоремы о дивергенции. Также это можно проверить численно. Я упоминаю об этом потому, что если вы решите разделить тело на маленькие плоскости, например на треугольники, и суммировать все гидростатические силы и их моменты, возникает искушение упростить расчёт моментов, как будто элементарные силы для каждого треугольника приложены к его центру (который легко найти).
Однако, если вы это сделаете, вы получите неправильный результат. Сила будет рассчитана правильно, но возникнет остаточный момент относительно центра погружённого объёма, при этом судно может накрениться в состоянии покоя даже на совершенно ровной поверхности воды. Это в особенности актуально при использовании низкополигональной сетки объекта для уменьшения ущерба производительности, потому что ошибка, сделанная для каждого треугольника, довольно значима. С другой стороны, при большом количестве маленьких треугольников ошибка, вызванная упрощением, значительно уменьшается, и упрощение может стать вполне допустимым. Но всегда существует компромисс между сложностью расчёта правильного центра и количеством треугольников в объекте. В Приложении A приведена формула расчёта расположения точки приложения гидростатических сил на погружённый в жидкость треугольник.
Два способа перевернуть лодку
В свете вышеизложенного, существует два способа расчёта выталкивающих сил. Объёмный способ: расчётом погружённого объёма и определением его центра тяжести. Поверхностный способ: определением погружённой поверхности и расчётом приложенной к ней силы. Эти два способа, при правильном применении, должны дать одинаковый результат.
И объёмный, и поверхностный способ без слишком большой аппроксимации требуют определения координат пересечения воды с корпусом судна. Это выглядит угрожающим, особенно если считать, что вода имеет не плоскую поверхность: расчёт выглядит слишком ресурсоёмким и сложным. Возможно поэтому многие склоняются к использованию объёмных примитивов. Например, сфер: в отличие от расчёта пересечения поверхности воды со сложной фигурой, расчёт объёма части сферы, погружённой в воду быстр и прост, если принять воду в непосредственной близости от сферы плоской. Объём даже можно определить аналитически, что означает (по крайней мере, теоретически), расчёт с бесконечной точностью, или с точностью, допускаемой операциями с плавающей запятой (да, в этой статье много игры слов). Кажется также, что погружённый объём будет изменяться постепенно и плавно при подъёме и опускании судна в воде, а постоянность физической модели часто предпочтительна в играх.
Но аппроксимация корпуса стандартного судна с помощью сфер может быстро превратиться в кошмар, потому что потребуется множество сфер различного диаметра. Поскольку сферы являются одними из наихудших вариантов для плотной упаковки в объём, у вас возникнут значительные пустоты между сферами (Рисунок 1). Существует верхний предел плотности упаковки в объём, даже для сфер с различным радиусом [5]. Наличие этих пустот приводит к заметному непостоянству при выталкивании. Сферы можно сделать пересекающимися, но тогда расчётный погружённый объём будет больше действительного. И наконец, в то время как расчёт пересечения плоской поверхности со сферой прост, расчёт пересечения сферы с произвольной поверхностью воды гораздо более труден, поэтому мы можем попытаться найти решение для расчёта пересечения корпуса судна с водой.

Рисунок 1 — Аппроксимация объёма судна с помощью сфер — это не решение.
Объём тела можно преобразовать в воксели, т.е. аппроксимизировать набором простых объёмных примитивов, например, кубов. Воксели, пересекающиеся с водой, также можно преобразовывать в меньшие воксели до достижения нужной точности. Проблема с аппроксимациями объёма в том, что они дают (достаточно грубые) ответы на вопрос «какое количество воды вытеснено?», но он довольно бесполезен для определения ватерлинии погружённого объекта, которая нужна, например, для применения спецэффектов воды, таких как брызги и пена, или для определения формы поверхности, контактирующей с водой, если вы конечно не используете совершенно неприемлемое их количество.
Предположив, что мы можем точно рассчитать поверхность корпуса, погружённую в воду, у нас всё равно остаётся выбор между объёмным и поверхностным способами расчёта. Для объёмного способа мы должны замкнуть погружённую поверхность корпуса, чтобы создать замкнутый объём, рассчитать его полный объём и центр тяжести, а затем приложить к нему выталкивающую силу. При поверхностном способе мы рассчитываем гидростатические силы давления, действующие на каждый погружённый элемент поверхности (треугольник), и суммируем их линейные импульсы и моменты импульса вокруг центра тяжести тела.
Преимущество поверхностного способа в том, что не требуется замыкать объём, всё уже готово к непосредственному суммированию сил. При объёмном способе погружённый объём может также состоять из нескольких объёмов. Его удобно использовать, например, для расчёта корпусов катамаранов. Однако даже есть судно не имеет отверстий, пересечение с водой должно представлять замыкание двух или более объёмов, и мы должны определить, к каким из объёмов относятся каждые из погружённых треугольников, что представляет собой дополнительную сложность при расчётах такого способа. Поверхностный подход в этом отношении более универсален, он работает вне зависимости от количества и формы образованных объёмов, и при этом не требует замыкания. Именно его я выбрал для своего алгоритма.
Структура алгоритма
Я объясню в общих чертах структуру алгоритма с некоторыми важными упрощениями, которые обеспечат быстрый расчёт и в то же время достаточные результаты.
Первое допущение, которое я сделаю, в том, что поверхность воды описывается какой-то сеткой из треугольников, вершины которых двигаются с каждым кадром в соответствии с движением воды. Конечно, это не всегда так, но всегда возможно аппроксимировать поверхность воды через сетку из треугольников. Позже в этой статье я расскажу, как взять поверхность воды и подготовить для неё представление в виде сетки треугольников вокруг тела.
Главной задачей будет определение координат пересечения между поверхностью воды и поверхностью корпуса судна. Рассмотрев реализацию Edouard Halbert [1], я начал реализовывать точное решение с учётом всех вариантов пересечения водной поверхности и треугольника. Эта проблема довольно сложна, потому что в теории существует множество способов разделения треугольника поверхностью. Поверхность может прорезать один треугольник в нескольких местах, проходить через центр, не касаясь ни одной из сторон, или погружая в себя любые из вершин. Каждый такой погружённый участок должен быть разбит на треугольники (триангулирован), но эти участки не обязательно являются выпуклыми, поэтому их сложнее триангулировать. Кроме того, такие случаи довольно часты. Даже в относительно спокойной воде они возникают очень часто и должны обрабатываться таким образом, чтобы они не привели к нереалистичной дискретности в размере поверхностей, считающихся погружёнными. Поработав какое-то время над реализацией совершенно точного, но очень медленного алгоритма расчёта пересечений, я понял, что нужно найти способы упрощения алгоритма, при этом не слишком жертвуя его общим поведением. Алгоритм, представленный мной здесь, является результатом таких упрощений. Я не буду рассказывать подробности первого (точного) алгоритма, потому что это чрезвычайно утомительно и скучно; кроме того, оптимизированный алгоритм работает отлично и рассчитывает порядок значения быстрее.
Оптимизированный алгоритм имеет следующую структуру: плавающее тело аппроксимируется при помощи сетки из треугольников (его корпуса). Мы определяем высоту над водой каждой вершины этого корпуса. Если высота отрицательна, значит, тело погружено в воду. Треугольники, все три вершины расположены над водой, считаются совершенно не погружёнными в воду. Это упрощение, в реальности вода может быть над поверхностью треугольника, но под всеми тремя вершинами (см. Рисунок 4). Также мы считаем треугольник полностью погружённым, если все три вершины находятся под водой, несмотря на то, что часть воды может находится под треугольником на какой-то части его площади. Если только одна или две вершины находятся под водой, мы разделяем треугольник на одну область под водой и одну область над водой, как показано на Рисунке 2. Если область под водой не является треугольником, мы триангулируем её. Я сделал смелое (и теоретически неверное) допущение, что поверхность воды пересекает сторону треугольника между погружённой и надводной вершинами только один раз. На Рисунке 3 показаны примеры случаев, когда пересечение рассчитывается неточно. В конце мы получаем список треугольников, каждый из которых погружён под воду. Затем мы рассчитываем гидростатические и гидродинамические силы, действующие на эти треугольники.

Рисунок 2 — 4 упрощённых случая пересечения треугольников с участком воды. Слева направо у треугольников погружены в воду, соответственно, 0, 1, 2 и 3 вершины. При 2 погружённых вершинах нам нужно ещё раз триангулировать погружённую часть. Следует учесть, что пересечение с водой не точное вследствие ещё одного упрощения, которое мы рассмотрим.

Рисунок 3 — Три примера случаев, неправильно обрабатываемых оптимизированным алгоритмом. Красными областями обозначены треугольники, которые должны считаться находящимися под водой, но не учитываемые. Два треугольника слева имеют пересечения с водой, но ни одна из их вершин не находится под водой. Треугольник посередине показан в перспективе, он не пересекается с водой ни одной стороной, однако верхушка волны проходит через середину треугольника. У треугольника справа две вершины находятся под водой, но вода также находится под треугольником на стороне между этими двумя вершинами.

Рисунок 4 — Пример случая, часто возникающего при ряби на воде. Больший правый нижний треугольник корпуса пересекает воду в нескольких областях, одна из которых не пересекает ни одну из сторон треугольника. Хуже того, пересекаемые области могли бы быть вогнутыми, при этом быстрая триангуляция стала бы ещё более сложной. Обработка всех таких случаев привела бы к затратам времени на разработку и производительности при работе игры. К тому же, это довольно бессмысленно, потому что, строго говоря, поверхность воды сама изменяется вследствие наличия судна.
Для модели судна такие случаи менее важны, чем кажется. На практике жертвование точностью не является проблемой, если размер треугольников корпуса не слишком большой относительно амплитуды и длины волн самых маленьких волн, которые мы хотим учитывать.
Основное преимущество предлагаемого подхода в том, что все вершины могут быть обработаны за первый проход, вне зависимости от того, какие из трёх формируют треугольник. После этого становится доступной вся информация, необходимая для обработки каждого треугольника, который служит основой для 0, 1 или 2 погружённых треугольников. Часть, посвящённая пересечению треугольников, очень простая и быстрая. БОльшая часть обработки при необходимости легко подвергается параллелизации. Также мы знаем максимальное количество погружённых треугольников, которое можно получить: в два раза больше количества треугольников корпуса объекта. Это позволяет нам выделить всю память заранее в простой массив.
В следующем разделе мы рассмотрим важные детали реализации, такие как способ аппроксимизации поверхности воды для оптимизации определения глубины воды, способ точного разделения треугольника, только одна или две вершины которого находятся под водой, а также расчёт выталкивающих сил.
Детали реализации
Участок воды
Для определения высоты над водой каждой вершины нам нужен быстрый способ определения положения воды под заданной точкой. Он во многом зависит от способа симуляции воды в игре или в её симуляции. Если вода плоская или описывается простой функцией, может быть быстрым способом просто определять высоту воды, замеряя или оценивая её при каждом запросе. Однако в других случаях алгоритм определения высоты воды ресурсоёмок и может быть сделано только ограниченное количество запросов. Например, такое бывает в случае методов, основанных на быстром преобразовании Фурье, таких как волны Тессендорфа [4].
В таком случае я предлагаю замерять высоту воды один раз в точках на одинаковом расстоянии от тела, создавая таким образом карту высот, которая будет затем использоваться для всех последующих запросов высот. Я буду называть эту карту высот «участком воды». Участок воды должен быть по крайней мере не меньше вертикальной проекции тела. Например, можно начать с квадратного участка воды, сторона которого равна диагонали прямоугольника, описанного вокруг проекции. Как и традиционная карта высот, участок воды состоит из прямоугольной области, разделённой на полосы, формирующие строки и столбцы, пересекающиеся в квадратных ячейках (Рисунки 5 и 6). Каждая ячейка сама разделена на 2 треугольника. Для каждого треугольника мы рассчитываем уравнение поверхности, на которой он находится, что позволяет очень быстро определить проекцию точки на неё.

Рисунок 5 — Участок воды размером 4×4 и ватерлиния (голубого цвета), показанные снизу.

Рисунок 6 — Участок воды размером 5×5 и ватерлиния (голубого цвета), показанные снизу.

Алгоритм разрезания
Когда часть вершин треугольника находится под водой, а часть — над водой, нам нужно разрезать его на кусок, полностью погружённый под воду, и кусок полностью над водой. Существует способ упростить разрезание, быстрый при расчётах и непрерывный. Под «непрерывностью» я имею в виду отсутствие ситуаций, когда небольшое изменение в высоте вершин приводит к неожиданно сильным изменениям в погружённой области. Эта проблема не возникла, если бы мы точно разрезали треугольники на подводные и надводные части, она появляется только из-за аппроксимации, и нам нужно выбрать тот способ, который хорошо себя ведёт. Эта проблема стала одной из первых моих препятствий, и иногда приводит к нестабильности в выталкивании, когда тело внезапно начинает значительно выпрыгивать или погружаться, разрушая весь эффект.





Рисунок 8 — Упрощённое разрезание треугольника, когда над водой находятся две вершины.




Расчёт гидростатических сил
После того, как алгоритм разрезания был выполнен для всех треугольников сетки объекта, мы получили список полностью погружённых треугольников. Выталкивающая сила, действующая на тело, является суммой всех гидростатических сил, действующих на каждый погружённый треугольник. Поскольку мы рассматриваем линейную силу, мы можем суммировать только вертикальную составляющую гидростатической силы, потому что мы видели, что остальные силы уравновешивают друг друга. Сила, действующая на погружённый треугольник, равна:


Не забывайте, что приложение гидростатической силы к центру треугольника вместо действительного центра её приложения приводит к остаточному вращающему моменту относительно центра вытесненного объёма. Если количество треугольников мало и важно не получать никакого вращающего момента, то необходимо рассчитать точку приложения силы к треугольнику. В Приложении A представлена формула определения центра приложения гидростатической силы к двум типам треугольников, чьё основание горизонтально, а вершина направлена вверх или вниз. Произвольно погружённый треугольник должен быть разрезан на два таких треугольника, после чего рассчитываются и суммируются два набора гидростатических сил и центров приложения сил.
Соединяем всё вместе
На Рисунке 10 представлено краткое описание алгоритма.

Рисунок 10 — Схема алгоритма.
Итак, мы можем резюмировать структуру алгоритма следующим образом (мы приняли, что x/z — это горизонтальная плоскость, а y — вертикальная ось, направленная вверх):
- На каждом шаге симуляции мы обновляем положение участка воды, чтобы следовать за плавающим телом. Как вы видите из анимированного gif на Рисунке 11, участок воды не следует плавно за судном. Когда судно движется горизонтально, оно сдвигается от исходного положения настолько, что участок воды теряет строку (или столбец) с одной стороны и добавляет строку (или столбец) с другой стороны. Когда это происходит, координаты участка воды (скажем, его юго-западный угол) резко изменяются по сравнению с предыдущим шагом.
- После определения координат участка воды для каждой точки сетки воды определяется или вычисляется высота воды.
- В каждой ячейке у нас есть два треугольника, образованные точками сетки, поднятыми в направлении y над высотой воды, как в традиционной карте высот. Вы вычисляем уравнения плоскостей, образованных таким способом.
- Затем мы рассчитываем высоту над водой каждой вершины корпуса, определяя, над каким треугольником они находятся и используя уравнение плоскости этого треугольника.
- Для каждого треугольника сетки объекта основываясь на высоте над водой каждой из его вершин, мы применяем алгоритм разрезания, создавая 0, 1 или 2 погружённых треугольника.
- И наконец мы проходим по всему списку погружённых треугольников для расчёта действующих на него сил (гидростатических и гидродинамических).
Разумеется, мы можем применить множество различных способов оптимизации. Например, мы можем сначала вертикально спроецировать вершины корпуса для точного определения задействованных треугольников ячеек и вычислять уравнения плоскостей только для этих треугольников.
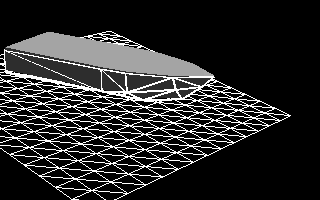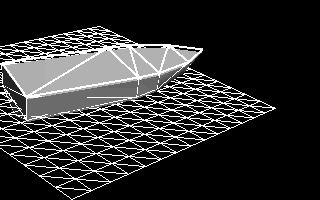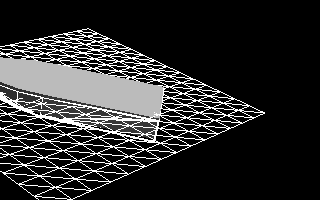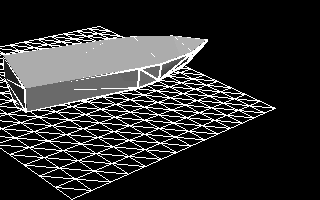
Рисунок 11 — Динамическое реагирование судна, на которое действуют только гидростатические силы на совершенно плоской поверхности воды.
Заключение
В данной статье приведёт алгоритм расчёта пересечения произвольной сетки с поверхностью воды и вычисления гидростатических сил, действующих на тело, описанное этой сеткой. Если бы вы написали программу только на основании этого алгоритма, то судно бы колебалось вверх и вниз, как будто на пружине. Судно бы выталкивалось из воды в воздух, затем падало под воздействием гравитации, погружалось в воду и снова выталкивалось из неё. Для стабилизации системы необходимо добавить затухание. Описываемые в следующей статье гидродинамические силы очень эффективны для добавления затуханий как в реальном мире. Но можно и схитрить, добавив затухание на основании высоких скоростей во всех направлениях движения, и в особенности в вертикальном направлении, чтобы появилось ощущение расчёта гидродинамических сил с помощью описанного выше алгоритма.
Примечания
(*) Если бы давление в точке заданной глубины было по каким-то причинам ниже относительно точек на той же глубине, то вода в точках на той же глубине, подвергающаяся большему давлению, очень быстро переместилась бы в точку с меньшим давлением и восстановила равномерное давление на этой глубине. Единственное, что мешает воде с повышенным давлением, находящейся на бОльшей глубине, подняться на глубину с меньшим давлением, является гравитация; именно поэтому существует градиент давлений, увеличивающийся при погружении.
(**) Кстати, когда я изучал эту теорему во Франции, она называлась теоремой Остроградского. Позже я узнал, что она также известна как теорема Гаусса. Я предполагаю (почти что в шутку), что причина этого в том, что французы не хотят связывать слишком много теорем с немцами, и при возможности выбора охотнее выбирают русский аналог. Американцы стремятся к практичности, и чтобы избежать долгих споров, называют её просто теоремой о дивергенции.
Приложение A. Гидростатические силы, действующие на погружённый в жидкость треугольник
Для расчёта гидростатических сил и моментов, действующих на полностью погружённый в жидкость треугольник, полезно разделить треугольник на треугольники меньшего размера, каждый из которых имеет абсолютно горизонтальную сторону. Причина этого в том, что гораздо проще рассчитать гидростатические силы, действующие на треугольник с горизонтальной стороной: он может быть разделён на (практически) прямоугольные горизонтальные полосы, на поверхности которых давление одинаково в любой точке.






Ссылки
1. Simship. Edouard Halbert.
2. «Buoyancy». Joel Feldman.
3. Hydrostatic forces on a plane surface.
4. Simulating Ocean Water. Jerry Tessendorf.
5. Upper Bounds For Packing Of Spheres Of Several Radii. David De Laat, Fernando Mario De Oliveira Filho, Frank Vallentin.
Об авторе: Жак Кернер (Jacques Kerner) — Senior Software Engineer в Avalanche Studios (Нью-Йорк), специалист по физике транспортных средств. Работал над играми Just Cause 3 (2015), Homefront (2011), Need for Speed: ProStreet (2007), Need for Speed: Carbon (2006).
