[Перевод] MCMC и байесова статистика в BASIC12.08.2015 14:49

BASIC был одним из самых распространенных языков программирования. В 80-х он шел в стандартном наборе программ на компьютере (например, Commodore 64 и Apple II), а в 90х и DOS и Windows 95 включали в себя QBasic IDE.

QBasic был также моим первым языком программирования. Я не программировал на Бейсике уже почти 20 лет и решил вспомнить этот действительно странный язык. Поскольку я провел много времени за байесовскими алгоритмами, я подумал, что будет интересно увидеть как байесовская аналитика будет выглядеть в утилите 20-летней давности.

Здесь мы реализуем алгоритм Метрополиса-Гастингса, стандартный метод Монте-Карло по схеме марковских цепей (MCMC), который используется в байесовских моделях, в Бейсике.

Я применил распределение Лапласа к самому очаровательному набору данных: количеству волчат на одну стаю. Выборка состояла из 16 стай. В итоге я подсчитал и вывел результат, по-прежнему используя Бейсик (источник).

Где достать BASIC

Есть много различных версий BASIC, но я взял тот, на котором вырос: Microsoft QBasic 1.1. QBasic имеет много расширенных функций таких как типы, определяемые пользователем и (внимание!) functions. Но я не использовал никаких дополнительных преференций, я ведь собирался писать олдскульный BASIC, используя строчную нумерацию и GOTO, что означает, что код можно легко импортировать в, скажем, Commodore 64 BASIC.

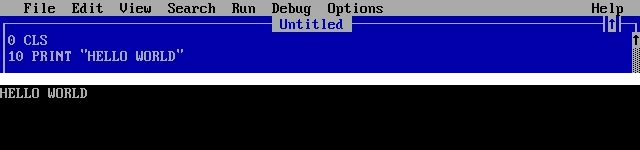
Скачать QBasic можно здесь. К тому же это бесплатно. Если конечно вы не используете DOS до сих пор, то следующим шагом будет установка эмулятора DOSBox. После того, как вы запустите QBASIC.EXE вашему взору предстанет очень дружественный, ярко-синий интерфейс. Его можно потестить с помощью кастомного скрипта. Он очистит экран и напечатает «HELLO WORLD».

Обратите внимание, что в QBasic нумерация строк не так важна, но в более старом BASIC (например в том, что стоял на Commodore 64) она необходима, поскольку программа выполняется по порядку.

Что мы будем реализовывать

Мы будем реализовывать алгоритм Метрополиса-Гастингса на классической MCMC, с которым вы столкнетесь в первую очередь, если будете изучать вычислительные методы для байесовских моделей.

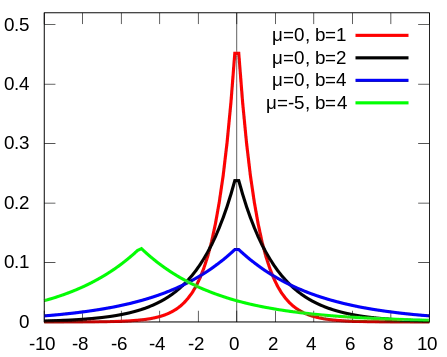
Байесовская модель, которую мы будем представлять, имеет простое одномерное распределение Лапласа (просто чтобы дать гауссовскому распределению отдохнуть). Распределение Лапласа, как и Гауссовское, конечно и симметрично, но имеет более острый пик и пологие хвосты.

Оно обладает двумя параметрами: параметр сдвига μ, который определяет также его среднее значение и медиану и размах b, который определяет ширину распределения.

В Лаплассовском распределении медиана является максимальной вероятностной оценкой параметра μ. Чтобы включить это в простейшую байесовскую модель мы должны иметь два параметрa. Здесь я буду упрощенно применять Uniform (−∞, ∞) к μ и log (b), это, P (μ), P (log (b))∝1. Полная модель:

x∼Laplace (μ, b)
μ∼Uniform (−∞, ∞)
log (b)∼Uniform (−∞, ∞)

Повторюсь, что данные, которые мы будем использовать, возможно самые милые, с которыми я работал. Они содержат количество волчат в выборке из 16 волчьих стай (source):

Реализация в R

Прежде чем углубиться в BASIC, реализуем все в R:

# Набор данных о волчатах
x <- c(5, 8, 7, 5, 3, 4, 3, 9, 5, 8, 5, 6, 5, 6, 4, 7)

# The log posterior density of the Laplace distribution model, when assuming 
# uniform/flat priors. The Laplace distribution is not part of base R but is
# available in the VGAM package.
model <- function(pars) {
  sum(VGAM::dlaplace(x, pars[1], exp(pars[2]), log = TRUE))
}

# The Metropolis-Hastings algorithm using a Uniform(-0.5, 0.5) proposal distribution 
metrop <- function(n_samples, model, inits) {
  samples <- matrix(NA, nrow = n_samples, ncol = length(inits))
  samples[1,] <- inits
  for(i in 2:n_samples) {
    curr_log_dens <- model(samples[i - 1, ])
    proposal <- samples[i - 1, ] + runif(length(inits), -0.5, 0.5)
    proposal_log_dens <- model(proposal)
    if(runif(1) < exp(proposal_log_dens - curr_log_dens)) {
      samples[i, ] <- proposal
    } else {
      samples[i, ] <- samples[i - 1, ]
    }
  }
  samples
}

samples <- metrop(n_samples = 1000, model, inits = c(0,0))
# Plotting a traceplot
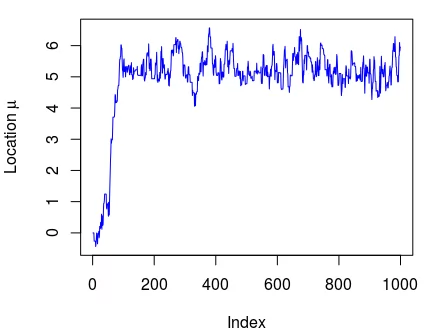
plot(samples[,1], type = "l", ylab = expression(Location ~ mu), col = "blue")
# Calculating median posterior and 95% CI discarding the first 250 draws as "burnin".
quantile(samples[250:1000,1], c(0.025, 0.5, 0.975))

##  2.5%   50% 97.5% 
## 4.489 5.184 6.144

(Этот скрипт просто показывает, что должно получиться на Бейсике. Если вы хотите попробовать метода Метрополиса-Гастингса на MCMC в R, воспользуйтесь MCMCmetrop1R в MCMCpack package, или этим Metropolis-Hastings script.

Модель в BASIC

Начнем с очистки экрана (CLS) и определения переменных. DIM определяет массивы и матрицы.

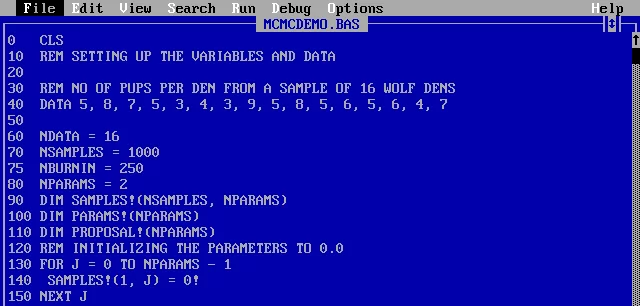
Даже в этом коротком куске кода можно обнаружить целую кучу странностей:

Поскольку мы пытаемся придерживаться олдскула, то везде стоит нумерация строк. Она не добавляется автоматически, а прописывается мной и иногда я пропускаю строчки. Отсюда хороший лайф-хак — каждый раз добавлять к строчке по 10, чтобы можно было вставить номер в пропущенную строку и не переписывать остальные (например 75 на скриншоте). Поскольку в старом Бейсике нет функций, нумерация строк будет использоваться командами GOSUB и GOTO.
Все операторы прописываются в верхнем регистре и если написать оператор в нижнем регистре, он исправится на верхний.
Почему SAMPLES! В QBasic все переменные являются числами и чтобы изменить их тип нужно добавить символ к имени переменной. Так что THIS$ это строка, а THAT! — это число с плавающей точкой. Поскольку параметры являются непрерывными, то большинство переменных будут заканчиваться на »!».
Команда DATA — это неплохой способ поместить данные в программу, позже их можно извлечь с помощью функции READ. Если у вас более одного набора данных, желаю удачи.

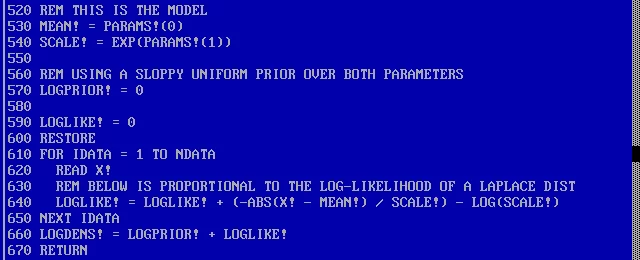
Продолжим определение модели. Мы представим ее в виде подпрограммы, которая заканчивается выражением RETURN . Она вызывается выражением GOSUB , которое переходит на , выполняет код до выражения RETURN и затем переходит на строку, которая идет после GOSUB. Это похоже на недо-функцию, которая не может передать аргументы или вернуть значения. Но все хорошо, пока все переменные глобальны. Подпрограмма может обращаться и устанавливать любые переменные, пока вы не используете одинаковые имена переменных для двух разных вещей. Подпрограмма ниже предполагает, что вектор PARAMS! перезаписывает переменную LOGDENS!. Подпрограмма также использует READ X!, чтобы считывать значения из DATA и RESTORE чтобы сбросить READ.

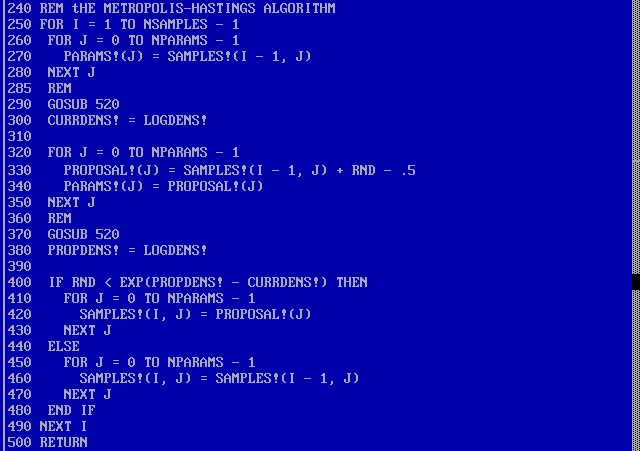
А вот и алгоритм Метрополиса-Гастингса. Ничего нового, кроме GOSUB 520, который используется чтобы перейти в подпрограмму модели на строку 520. Далее мы используем RND, чтобы равномерно сгенерировать рандомные числа в промежутке от 0 до 1.

Подсчет и вывод на экран

Теперь можно собрать все вместе с помощью следующего кода:

Код ниже берет матрицу SAMPLES! и рассчитывает среднее значение, стандартное отклонение и 95 интервал доверия.

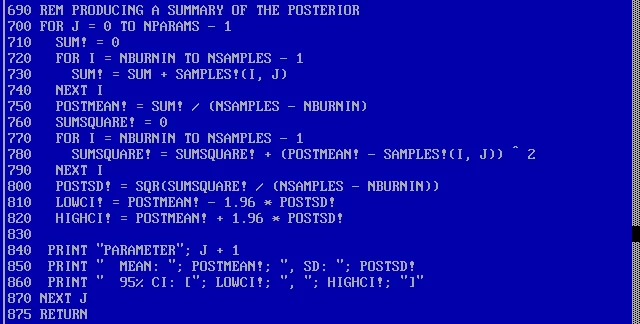
Еще немного странностей от Бейсика: PRINT «HELLO», «YOU!» выведет на экран HELLO YOU!, а PRINT «HELLO»; «YOU!» выведет HELLOYOU! Разделитель »,» или »;» определяет будет ли пробел между выводимыми объектами.

И наконец мы хотим вывести график, чтобы удостоверится, что цепь Маркова выглядит нормально. И хоть в Бейсике нет даже встроенной функции для сортировки, зато есть колоссальная поддержка графики. Кусок кода ниже просто масштабирует координаты выборки, чтобы они подходили под разрешение 320×200. Обратите внимание на забавный синтаксис для отрисовки линий: LINE (, )-(, ).

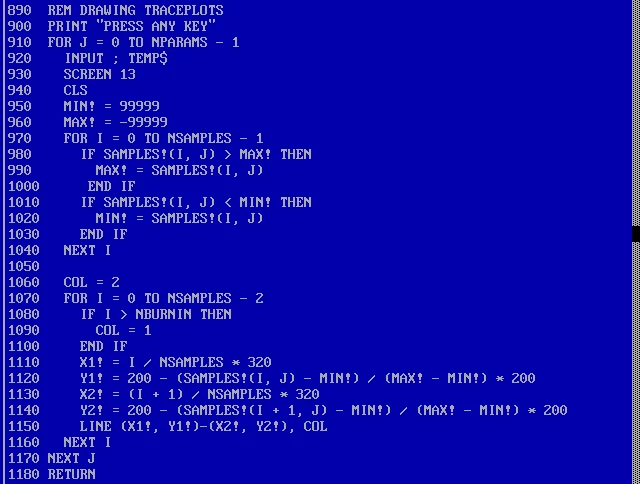
Мы наверное захотим записать реализацию на диск:

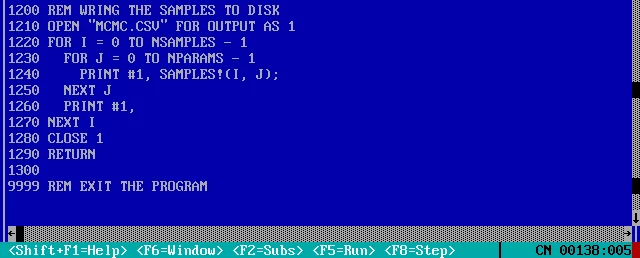
Выполнение

Теперь наконец мы готовы собрать все воедино, сформировать и вывести.

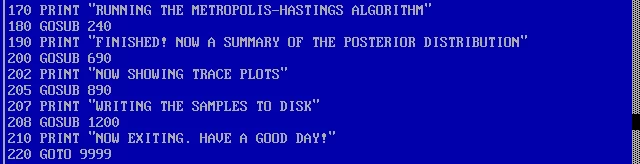
Самый нижний GOTO просто переходит на последнюю строку программы, чтобы выйти из нее. Если мы установим эмуляцию скорости 33 MHz, как в 386 компе (согласно этой странице), то генерация выборки, подсчет и вывод займут около минуты. Вот результат:

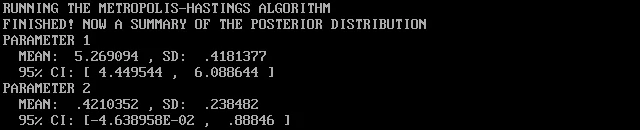
Так что там с волчатами

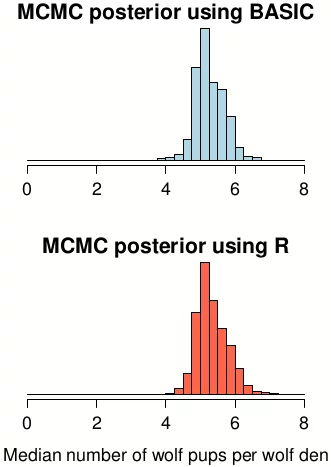
Этот пример был не совсем об анализе данных, но глядя на результаты можно предположить, что среднее количество щенков в стае колеблется от 4–5 до 6. Я должен также отметить, что обе реализации на BASIC и на R похожи:

Здесь полная программа в текстовом формате (MCMCDEMO.BAS),

Конспект

Мы можем работать с довольно продвинутой байесовой статистикой с помощью утилиты, которую использовали 20 лет назад.
Программирование с помощью GOTO и GOSUB очень-очень олдскульное.
Очень приятно не писать множество скобок (Но с другой строны приходится писать буквенные END IF и NEXT I.)
Запуск программы на 386 компьютере прошел довольно быстро.
Очень тяжело писать код, когда все переменные глобальны.