[Перевод] Математики доказали, что многочлены не помогут взломать RSA

Недавно в журнале Quanta вышел материал, в котором автор рассказывал про удивительный с точки зрения неискушенных читателей феномен, доказанный математиками. Его суть в том, что почти все многочлены определенного типа — неприводимые, то есть не поддаются разложению. Это доказательство применяется во многих областях чистой математики. Но также это хорошая новость для одного из столпов современной жизни — цифрового шифрования.
Для надежного хранения цифровой информации широко используется шифрование с помощью алгоритма RSA. Это прокачанная версия схемы, которую может придумать даже семиклассник, чтобы обмениваться сообщениями с друзьями: каждой букве присваивается свой номер, который умножается на некий секретный, заранее оговоренный ключ. Чтобы расшифровать сообщение, достаточно просто поделить его на секретный ключ.
RSA-шифрование работает схожим образом. Приведем сильно упрощенное объяснение. Пользователь придумывает сообщение и выполняет над ним определенные математические операции, включающие в себя умножение на очень большое число (длиной в несколько сотен цифр). Единственный способ расшифровать сообщение — найти простые множители полученного результата*.
Простые множители какого-либо числа — это простые числа, которые необходимо перемножить, чтобы получилось это число. Так, для числа 12 это 2×2*3, а для числа 495 это 3, 3, 5 и 11.
Безопасность RSA-шифрования базируется на том факте, что математике неизвестны быстрые способы найти простые множители очень больших чисел. И если зашифрованное сообщение предназначалось не вам, и у вас нет ключа для его расшифровки, то попытки найти этот ключ могут занять добрую тысячу лет. Причем это справедливо и для самых современных компьютеров, с помощью которых все равно не удастся подобрать правильные простые множители.
Но есть и обходной путь. Каждое число может быть представлено в виде уникального алгебраического уравнения. И, в отличие от поиска простых множителей числа, поиск простых множителей многочлена выполнить гораздо легче. И как только многочлен будет разложен на такие простые множители, эту информацию можно использовать для поиска простых множителей первоначального числа.
Вот как это работает.
Шаг первый: Выбирается любое число, простые множители которого нужно узнать. Для простоты возьмем число 15.
Шаг второй: 15 переводится в двоичную систему:
1111.
Шаг третий: Это двоичное выражение превращается в многочлен путем перевода всех двоичных чисел в коэффициенты многочлена:
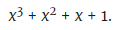
(Обратите внимание: этот многочлен равен 15, если x=2. Число 2 — основание двоичной системы.)
Шаг четвертый: Многочлен раскладывается на множители:
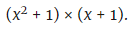
Шаг пятый: x=2 подставляется в каждый из этих множителей:
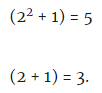
Заключение: 5 и 3 — простые множители числа 15.
Да, это излишне сложный способ поиска простых множителей небольшого числа вроде 15, которые легко вычислить в уме. Однако когда дело доходит до крупных чисел, состоящих из сотен цифр, этот многочленный метод дает удивительное преимущество. Для разложения простых чисел быстрых алгоритмов не существует. Но для разложения крупных многочленов такие алгоритмы есть. Поэтому как только удастся превратить большое число в большой многочлен, можно очень близко подобраться к поиску простых множителей числа.
Означает ли это, что RSA-шифрование находится под угрозой? На самом деле нет. И новая, недавно доказанная закономерность по поводу многочленов как раз связана с этим.
Математики Эммануэль Брулья и Петер Варью из Кембриджского университета доказали, что по мере удлинения многочленов с коэффициентами 0 и 1 вероятность того, что их вообще можно будет разложить, становится все ниже. А если многочлен не удастся разложить, значит, его нельзя будет использовать для поиска простых множителей числа, которое требуется вычислить.
Доказательство Брулья и Варью фактически говорит о том, что обходной путь для взлома RSA-шифрования ведет в никуда. Используемые в RSA очень большие числа соответствуют очень длинным многочленам. Кембриджские ученые утверждают, что практически невозможно найти многочлены такой длины, поддающиеся при этом разложению. Как криптографы, так и математики давно подозревали, что это так. Однако когда мировая кибербезопасность зависит от невозможности использования некоторого математического приема, всегда хорошо иметь доказательство, что этот прием действительно не работает.

