[Перевод] Learn OpenGL. Урок 6.4 – IBL. Зеркальная облученность14.11.2018 13:47

OGL3
В предыдущем уроке мы подготовили нашу модель PBR для работы вместе с методом IBL — для этого нам потребовалось заранее подготовить карту облученности, которая описывает диффузную часть непрямого освещения. В этом уроке мы обратим внимание на вторую часть выражения отражающей способности — зеркальную:

$L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i$

Содержание

Можно заметить, что зеркальная составляющая Кука-Торренса (подвыражение с множителем $k_s$ ) не является постоянной и зависит от направления падающего света, а также от направления наблюдения. Решение этого интеграла для всех возможных направлений падения света вкупе со всеми возможными направлениями наблюдения в реальном времени просто неосуществимо. Поэтому исследователи Epic Games предложили подход, названый аппроксимацией раздельной суммой (split sum approximation), позволяющий заранее частично подготовить данные для зеркальной компоненты, при соблюдении некоторых условий.

В этом подходе зеркальная компонента выражения отражающей способности разделяется на две части, которые можно подвергнуть предварительной свертке по отдельности, а затем объединить в PBR шейдере, для использования в качестве источника непрямого зеркального излучения. Также как и в случае с формированием карты облученности, процесс свертки принимает HDR карту окружения на своем входе.

Для понимания метода приближения раздельной суммой взглянем еще раз на выражение отражающей способности, оставив в нем только подвыражение для зеркальной компоненты (диффузная часть была рассмотрена отдельно в предыдущем уроке):

$L_o(p,\omega_o) = \int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} L_i(p,\omega_i) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i$

Как и в случае с подготовкой карты облученности данный интеграл нет никакой возможности решать в реальном времени. Потому желательно аналогичным образом предрассчитать карту для зеркальной составляющей выражения отражающей способности, а в основном цикле рендера обойтись простой выборкой из этой карты на основе нормали к поверхности. Однако, все не так просто: карта облученности получалась относительно легко за счет того, что интеграл зависел лишь от $\omega_i$ , а постоянное подвыражение для Ламбертовской диффузной составляющей можно было вынести за знак интеграла. В данном же случае интеграл зависит не только от $\omega_i$ , что легко понять из формулы BRDF:

$f_r(p, w_i, w_o) = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}$

Выражение под интегралом зависит также и от $\omega_o$ — по двум векторам направления осуществить выборку из предварительно подготовленной кубической карты практически невозможно. Положение точки $p$ в данном случае можно не учитывать — почему это так было рассмотрено в предыдущем уроке. Предварительный расчет интеграла для всех возможных сочетаний $\omega_i$ и $\omega_o$ невозможен в задачах реального времени.

Метод раздельной суммы от Epic Games решает эту проблему путем разбиения задачи предварительного расчета на две независимые части, результаты которых можно объединить позже для получения итогового предрассчитанного значения. Метод раздельной суммы выделяет два интеграла из исходного выражения для зеркальной компоненты:

$L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i$

Результат расчета первой части обычно называется предварительно отфильтрованной картой окружения (pre-filtered environment map), и является картой окружения, подвергнутой процессу свертки, заданному этим выражением. Все это схоже с процессом получения карты облученности, однако в этом случае свертка ведется с учетом значения шероховатости. Высокие значения шероховатости приводят к использованию более разрозненных векторов выборки в процессе свертки, что порождает более размытые результаты. Результат свертки для каждого следующего выбранного уровня шероховатости сохраняется в очередном мип-уровне подготавливаемой карты окружения. Например, карта окружения, подвергнутая свертке для пяти различных уровней шероховатости, содержит пять мип-уровней и выглядит примерно так:

Вектора выборки и их величина разброса определяются на основе функции нормального распределения (NDF) модели BRDF Кука-Торренса. Данная функция принимает вектор нормали и направление наблюдения как входные параметры. Поскольку направление наблюдения заранее неизвестно в момент предварительного расчета, то разработчикам Epic Games пришлось сделать еще одно допущение: направление взгляда (а значит, и направление зеркального отражения) всегда идентично выходному направлению выборки $\omega_o$ . В виде кода:

vec3 N = normalize(w_o);
vec3 R = N;
vec3 V = R;

В таких условиях направление взгляда не потребуется в процессе свертки карты окружения, что делает расчет выполнимым в реальном времени. Но с другой стороны мы лишаемся характерного искажения зеркальных отражений при наблюдении под острым углом к отражающей поверхности, что видно на изображении ниже (из публикации Moving Frostbite to PBR). В общем и целом, такой компромисс считается допустимым.

Вторая часть выражения раздельной суммы содержит BRDF исходного выражения для зеркальной компоненты. Если допустить, что входящая энергетическая яркость спектрально представлена белым светом для всех направлений (т.е., $L(p, x) = 1.0$ ), то возможно предварительно рассчитать значение для BRDF при следующих входных параметрах: шероховатость материала и угол меду нормалью $n$ и направлением света $\omega_i$ (или же $n \cdot \omega_i$ ). Подход Epic Games предполагает хранение результатов вычисления BRDF для каждого сочетания шероховатости и значения угла между нормалью и направлением света в виде двухмерной текстуры, известной как карта комплексирования BRDF (BRDF integration map), которая позже используется как справочная таблица (look-up table, LUT). Данная справочная текстура использует красный и зеленый выходные каналы для хранения масштаба и смещения для расчета коэффициента Френеля поверхности, что в итоге позволяет решить и вторую часть выражения раздельной суммы:

Данная вспомогательная текстура создается следующим образом: текстурные координаты по горизонтали (в пределах от [0., 1.]) рассматриваются как значения входного параметра $n \cdot \omega_i$ функции BRDF; текстурные координаты по вертикали рассматриваются как входные значения шероховатости.

В итоге, имея такую карту комплексирования и предварительно обработанную карту окружения, можно скомбинировать выборки из них для получения итогового значения интегрального выражения зеркальной компоненты:

float lod             = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF          = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)

Данный обзор метода раздельной суммы от Epic Games должен помочь составить впечатление о процессе приближенного вычисления части выражения отражающей способности, отвечающей за зеркальную компоненту. Теперь же попробуем подготовить данные карты самостоятельно.

Предварительная фильтрация HDR карты окружения

Предварительная фильтрация карты окружения идет схожим образом с тем, что было сделано для получения карты облученности. Разница заключается лишь в том, что сейчас мы учитываем шероховатость и сохраняем результат для каждого уровня шероховатости в новом мип-уровне кубической карты.

Для начала придется создать новую кубическую карту, которая будет содержать результат предварительной фильтрации. Для того, чтобы создать необходимое число мип-уровней мы попросту вызовем glGenerateMipmaps () — необходимый запас памяти будет выделен для текущей текстуры:

unsigned int prefilterMap;
glGenTextures(1, &prefilterMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, prefilterMap);
for (unsigned int i = 0; i < 6; ++i)
{
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); 
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

Обратите внимание: поскольку выборка из prefilterMap будет вестись с учетом существования мип-уровней, то необходимо установить режим фильтра уменьшения в режим GL_LINEAR_MIPMAP_LINEAR, чтобы включить трилинейную фильтрацию. Предварительно обработанные образы зеркальных отражений хранятся в отдельных гранях кубической карты с разрешением на базовом мип-уровне всего 128×128 пикселей. Для большинства материалов этого вполне хватает, однако, если в вашей сцене повышенное количество гладких, блестящих поверхностей (например, новенькая машина), вам может потребоваться увеличение этого разрешения.

В предыдущем уроке мы провели свертку карты окружения путем создания векторов выборки, которые равномерно распределены в полусфере $\Omega$ , используя сферические координаты. Для получения облученности этот метод вполне эффективен, чего не скажешь о расчетах зеркальных отражений. Физика зеркальных бликов подсказывает нам, что направление зеркально отраженного света прилегает к вектору отражения $r$ для поверхности с нормалью $n$ , даже если шероховатость не равна нулю:

Обобщенная форма возможных исходящих направлений отражения называется зеркальным лепестком (specular lobe; «лепесток зеркальной диаграммы направленности» — пожалуй, слишком многословно, прим.пер.). С ростом шероховатости лепесток увеличивается, расширяется. Также его форма меняется в зависимости от направления падения света. Таком образом, форма лепестка сильно зависит от свойств материала.

Возвращаясь к модели микроповерхностей, можно себе представить форму зеркального лепестка как описывающую ориентацию отражения относительно медианного вектора микро-поверхностей, с учетом некоторого заданного направления падения света. Понимая, что большая часть лучей отраженного света лежит внутри зеркального лепестка, сориентированного на основе медианного вектора, имеет смысл создавать вектора выборки, сориентированные сходным образом. Иначе многие из них окажутся бесполезными. Такой подход называется выборкой по значимости (importance sampling).

Интегрирование методом Монте-Карло и выборка по значимости

Для полного понимания сути выборки по значимости придется сначала ознакомиться с таким математическим аппаратом, как метод интегрирования Монте-Карло. Данный метод основывается на сочетании статистики и теории вероятности и помогает провести численное решение некоторой статистической задачи на большой выборке без необходимости рассмотрения каждого элемента этой выборки.

Например, вы хотите подсчитать средний рост населения страны. Для получения точного и достоверного результата пришлось бы измерить рост каждого гражданина и усреднить результат. Однако, поскольку население большей части стран довольно велико данный подход практически нереализуем, поскольку требует слишком много ресурсов на исполнение.
Другой подход заключается в создании меньшей подвыборки, наполненной истинно случайными (несмещенными) элементами исходной выборки. Далее вы также измеряете рост и усредняете результат для этой подвыборки. Можно взять хоть всего сотню людей и получить результат, пусть и не абсолютно точный, но все же достаточно близкий к реальной ситуации. Объяснение этому методу лежит в рассмотрении закона больших чисел. И суть его описывается таким образом: результат некоторого измерения в меньшей подвыборке размера $N$ , составленной из истинно случайных элементов исходного множества, будет приближен к контрольному результату измерения, проведенного на всем исходном множестве. Причем приблизительный результат стремится к истинному с ростом $N$ .
Интегрирование методом Монте-Карло является приложением закона больших чисел для решения интегралов. Вместо решения интеграла с учетом всего (возможно бесконечного) множества значений $x$ , мы используем $N$ случайных точек выборки и усредняем результат. С ростом $N$ приблизительный результат гарантированно будет приближаться к точному решению интеграла.

$O = \int\limits_{a}^{b} f(x) dx = \frac{1}{N} \sum_{i=0}^{N-1} \frac{f(x)}{pdf(x)}$

Для решения интеграла получается значение подынтегральной функции для $N$ случайных точек из выборки в пределах [a, b], результаты суммируются и делятся на общее число взятых точек для усреднения. Элемент $pdf$ описывает функцию плотности вероятности (probability density function), которая показывает с какой вероятностью каждое выбранное значение встречается в исходной выборке. Например, данная функция для роста граждан выглядела бы примерно так:

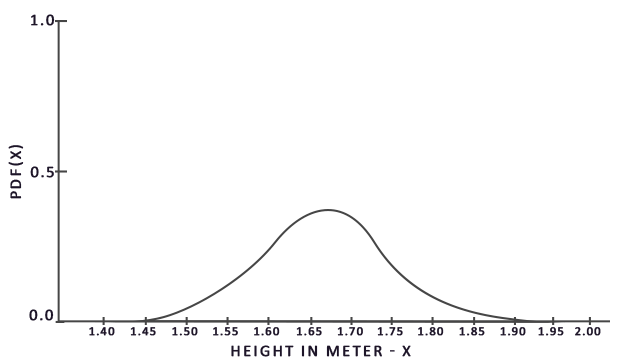
Видно, что при использовании случайных точек выборки у нас гораздо выше шанс встретить значение роста в 170 см, чем кого-то с ростом 150 см.

Ясно, что при проведении интегрирования методом Монте-Карло некоторые точки выборки имеют больше шансов появиться в последовательности, нежели другие. Поэтому в любом выражении для оценки методом Монте-Карло мы делим или умножаем отобранную величину на вероятность её появления, используя функцию плотности вероятности. На данный момент при оценке интеграла мы создавали множество равномерно распределенных точек выборки: шанс получения любой из них был одинаков. Таким образом наша оценка была несмещенной (unbiased), что означает, что при росте количества точек выборки наша оценка будет сходиться к точному решению интеграла.

Однако, есть оценочные функции, являющиеся смещенными (biased), т.е. подразумевающими создание точек выборки не в истинно случайной манере, а с преобладанием некоторой величины или направления. Такие функции оценки позволяют оценке методом Монте-Карло сходиться к точному решению гораздо быстрее. С другой стороны, из-за смещенности функции оценки, решение может и не сойтись никогда. В общем случае это считается приемлемым компромиссом, особенно в задачах компьютерной графики, поскольку оценка очень близкая к аналитическому результату и не требуется, если визуально его эффект выглядит достаточно достоверно. Как мы скоро увидим выборка по значимости (использующая смещенную функцию оценки) позволяет создавать точки выборки, смещенные в сторону определенного направления, что учитывается с помощью умножения или деления каждого выбранного значения на соответствующее значение функции плотности вероятности.

Интегрирование Монте-Карло довольно часто встречается в задачах компьютерной графики, поскольку является достаточно интуитивным методом оценки значения непрерывных интегралов численным методом, который достаточно эффективен. Достаточно взять некоторую площадь или объем в которой ведется выборка (например, наша полусфера $\Omega$ ), создать $N$ случайных точек выборки, лежащих внутри, и провести взвешенное суммирование полученных значений.

Метод Монте-Карло — весьма обширная тема для обсуждения и здесь мы более не будем углубляться в детали, однако остается еще одна важная деталь: существует отнюдь не один способ создания случайных выборок. По умолчанию, каждая точка выборки является полностью (псведо)случайной — чего мы и ожидаем. Но, используя определенные свойства квазислучайных последовательностей есть возможность создать наборы векторов, которые хоть и случайны, но обладают интересными свойствами. Например, при создании случайных выборок для процесса интегрировании можно использовать так называемые последовательности низкого несоответствия (low-discrepancy sequences), которые обеспечивают случайность созданных точек выборки, но в общем наборе они более равномерно распределены:

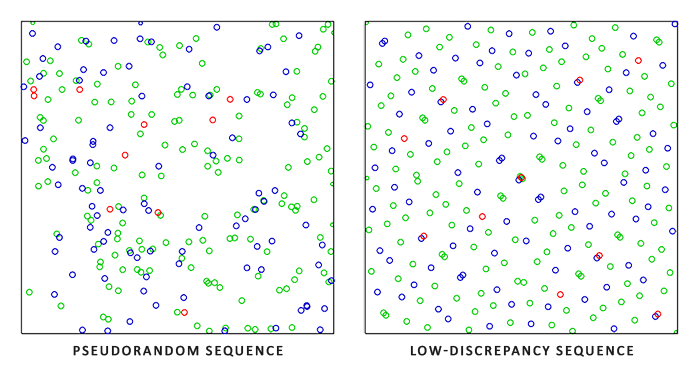
Использование последовательностей низкого несоответствия для создания набора векторов выборки для процесса интеграции является квази-методом Монте-Карло (Quasi-Monte Carlo intergration). Квази-методы Монте-Карло сходятся гораздо быстрее общего подхода, что весьма заманчивое свойство для приложений с высокими требованиями к производительности.

Итак, мы знаем об общем и квази-методе Монте-Карло, но есть еще одна деталь, которая обеспечит еще бОльшую скорость сходимости: выборка по значимости.
Как уже было отмечено в уроке, для зеркальных отражений направление отраженного света заключено в зеркальном лепестке, размер и форма которого зависит от шероховатости отражающей поверхности. Понимая, что любые (квази)случайные векторы выборки, оказавшиеся вне зеркального лепестка не окажут влияния на интегральное выражение зеркальной компоненты, т.е. бесполезны. Имеет смысл генерацию векторов выборки сфокусировать в области зеркального лепестка, используя смещенную функцию оценки для метода Монте-Карло.

В этом и заключается суть выборки по значимости: создание векторов выборки заключено в некоторой области, сориентированной вдоль медианного вектора микро-поверхностей, и форма которой определенна шероховатостью материала. Используя сочетание квази-метода Монте-Карло, последовательностей низкого несоответствия и смещения процесса создания векторов выборки за счет выборки по значимости, мы достигает очень высоких скоростей сходимости. Поскольку схождение к решению достаточно быстрое, то мы можем использовать меньшее количество векторов выборки при достижении все еще достаточно приемлемой оценки. Описанная комбинация методов, в принципе, позволяет графическим приложениям даже решать интеграл зеркальной компоненты в реальном времени, хотя предварительный расчет все еще остается значительно более выгодным подходом.

Последовательность низкого несоответствия

В этом уроке мы все же используем предварительный расчет зеркальной компоненты выражения отражающей способности для непрямого излучения. И использовать будем выборку по значимости с применением случайной последовательности низкого несоответствия и квази-метод Монте-Карло. Используемая последовательность известна как последовательность Хаммерсли (Hammersley sequence), подробное описание которой дано Holger Dammertz. Данная последовательность, в свою очередь, основана на последовательности ван дер Корпута (van der Corput sequence), которая использует специальное преобразование двоичной записи десятичной дроби относительно десятичной точки.

Используя хитрые трюки побитовой арифметики можно довольно эффективным образом задать последовательность ван дер Корпута прямо в шейдере и на её основе создавать i-ый элемент последовательности Хаммерсли из выборки в $N$ элементов:

float RadicalInverse_VdC(uint bits) 
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}

Функция Hammersley ()возвращает i-ый элемент последовательности низкого несоответствия из множества выборок размера $N$ .

Не все драйверы OpenGL поддерживают побитовые операции (WebGL и OpenGL ES 2.0, например), так что для определенных окружений может потребоваться альтернативная реализация их использования:
float VanDerCorpus(uint n, uint base)
{
    float invBase = 1.0 / float(base);
    float denom   = 1.0;
    float result  = 0.0;

    for(uint i = 0u; i < 32u; ++i)
    {
        if(n > 0u)
        {
            denom   = mod(float(n), 2.0);
            result += denom * invBase;
            invBase = invBase / 2.0;
            n       = uint(float(n) / 2.0);
        }
    }

    return result;
}
// ----------------------------------------------------------------------------
vec2 HammersleyNoBitOps(uint i, uint N)
{
    return vec2(float(i)/float(N), VanDerCorpus(i, 2u));
}
Отмечу, что из-за определенных ограничений на операторы циклов в старом железе, данная реализация проходится по всем 32 битам. В итоге данная версия не такая производительная, как первый вариант — зато работает на любом железе и даже в отсутствие битовых операций.

Выборка по важности в модели GGX

Вместо равномерного или случайного (по Монте-Карло) распределения генерируемых векторов выборки внутри полусферы $\Omega$ , фигурирующей в решаемом нами интеграле, мы попробуем создавать вектора так, чтобы они тяготели к основному направлению отражения света, характеризуемого медианным вектором микроповерхностей и зависящего от шероховатости поверхности. Сам процесс выборки будет схож с ранее рассмотренным: откроем цикл с достаточно большим количеством итераций, создадим элемент последовательности низкого несоответствия, на его основе создадим вектор выборки в касательном пространстве, перенесем этот вектор в мировые координаты и используем для выборки значения энергетической яркости сцены. В принципе, изменения касаются лишь того, что теперь применяется элемент последовательности низкого несоответствия для задания нового вектора выборки:

const uint SAMPLE_COUNT = 4096u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
    vec2 Xi = Hammersley(i, SAMPLE_COUNT);

Кроме того, для полного формирования вектора выборки потребуется каким-то образом его сориентировать в направлении зеркального лепестка, соответствующего заданному уровню шероховатости. Можно взять NDF (функция нормального распределения) из урока, посвящённого теории и скомбинировать с GGX NDF для метода задания вектора выборки в сфере за авторством Epic Games:

vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
    float a = roughness*roughness;
        
    float phi = 2.0 * PI * Xi.x;
    float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
    float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
        
    // преобразование из сферических в декартовы координаты
    vec3 H;
    H.x = cos(phi) * sinTheta;
    H.y = sin(phi) * sinTheta;
    H.z = cosTheta;
        
    // преобразование из касательного пространства в мировые координаты
    vec3 up        = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
    vec3 tangent   = normalize(cross(up, N));
    vec3 bitangent = cross(N, tangent);
        
    vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
    return normalize(sampleVec);
}

В результате получится вектор выборки, приблизительно сориентированный вдоль медианного вектора микроповерхностей, для заданной шероховатости и элемента последовательности низкого несоответствия Xi. Обратите внимание, что Epic Games использует квадрат величины шероховатости для большего визуального качества, что основано на оригинальной работе Disney о методе PBR.

Закончив реализацию последовательности Хаммерсли и кода генерации вектора выборки, мы можем привести код шейдера предварительной фильтрации и свертки:

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform samplerCube environmentMap;
uniform float roughness;

const float PI = 3.14159265359;

float RadicalInverse_VdC(uint bits);
vec2 Hammersley(uint i, uint N);
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness);
  
void main()
{               
    vec3 N = normalize(localPos);    
    vec3 R = N;
    vec3 V = R;

    const uint SAMPLE_COUNT = 1024u;
    float totalWeight = 0.0;   
    vec3 prefilteredColor = vec3(0.0);     
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(dot(N, L), 0.0);
        if(NdotL > 0.0)
        {
            prefilteredColor += texture(environmentMap, L).rgb * NdotL;
            totalWeight      += NdotL;
        }
    }
    prefilteredColor = prefilteredColor / totalWeight;

    FragColor = vec4(prefilteredColor, 1.0);
}

Мы осуществляем предварительную фильтрацию карты окружения на основе некоторой заданной шероховатости, уровень которой изменяется для каждого мип-уровня результирующей кубической карты (от 0.0 до 1.0), а результат фильтра сохраняем в переменной prefilteredColor. Далее переменная делится на суммарный вес для всей выборки, причем сэмплы с меньшим вкладом в итоговый результат (имеющие меньшее значение NdotL) также меньше увеличивают и итоговый вес.

Сохранение данных предварительной фильтрации в мип-уровнях

Остается написать код, непосредственно поручающий OpenGL фильтрацию карты окружения с различными уровнями шероховатости и последующим сохранением результатов в череде мип-уровней целевой кубической карты. Здесь как нельзя кстати пригодится уже подготовленный код из уроке об расчете карты облученности:

prefilterShader.use();
prefilterShader.setInt("environmentMap", 0);
prefilterShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
unsigned int maxMipLevels = 5;
for (unsigned int mip = 0; mip < maxMipLevels; ++mip)
{
    // уточняем размер фреймбуфера на основе текущего номера мип-уровня
    unsigned int mipWidth  = 128 * std::pow(0.5, mip);
    unsigned int mipHeight = 128 * std::pow(0.5, mip);
    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, mipWidth, mipHeight);
    glViewport(0, 0, mipWidth, mipHeight);

    float roughness = (float)mip / (float)(maxMipLevels - 1);
    prefilterShader.setFloat("roughness", roughness);
    for (unsigned int i = 0; i < 6; ++i)
    {
        prefilterShader.setMat4("view", captureViews[i]);
        glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 
                               GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, prefilterMap, mip);

        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        renderCube();
    }
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);

Процесс похож на свертку карты облученности, однако в этот раз следует на каждом шаге уточнить размер кадрового буфера, уменьшая его в два раза для соответствия мип-уровням. Также мип-уровень, в который будет вестись рендер в данный момент необходимо указать в качестве параметра функции glFramebufferTexture2D ().

Результатом выполнения данного кода должна стать кубическая карта, содержащая все более размытые изображения отражений на каждом последующем мип-уровне. Можно использовать такую кубическую карту как источник данных для скайбокса и взять выборку из любого мип-уровня далее нулевого:

vec3 envColor = textureLod(environmentMap, WorldPos, 1.2).rgb;

Результатом такого действия будет следующая картина:

Выглядит как сильно размытая исходная карта окружения. Если у вас результат схож, то, верней всего, процесс предварительной фильтрации HDR карты окружения выполнен верно. Попробуйте поэкспериментировать с выборкой из разных мип-уровней и понаблюдать постепенный рост размытости с каждым следующим уровнем.

Артефакты свертки предварительной фильтрации

Для большинства задач описанный подход работает достаточно хорошо, но рано или поздно придется встретиться с различными артефактами, которые порождает процесс предварительной фильтрации. Здесь перечислены самые распространенные и методы борьбы с ними.

Проявление швов кубической карты

Выборка значений из обработанной предварительным фильтром кубической карты для поверхностей с высокой шероховатостью приводит к считыванию данных из мип-уровня где-то ближе к концу их цепочки. При выборке из кубических карты OpenGL по умолчанию не осуществляет линейной интерполяции между гранями кубической карты. Поскольку высокие мип-уровни обладают меньшим разрешением, а карта окружения была подвергнута свертке с учетом сильно бОльшего зеркального лепестка, отсутствие текстурной фильтрации между гранями становится очевидным:

К счастью, в OpenGL встроена возможность активации такой фильтрации простым флагом:

glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS);

Достаточно установить флаг где-то в коде инициализации приложения и с этим артефактом покончено.

Появление ярких точек

Поскольку зеркальные отражения в общем случае содержат высокочастотные детали, а также области с сильно отличающимися яркостями, то их свертка требует использования большого числа точек выборки для корректного учета большого разброса значений внутри HDR отражений от окружения. В примере мы и так берем достаточно большое число сэмплов, но для определенных сцен и высоких уровней шероховатости материала этого все равно не будет достаточно, и вы станете свидетелем появлению множества пятен вокруг ярких областей:

Можно и дальше увеличивать количество сэмплов, но это не будет универсальным решением и в каких-то условиях все равно допустит артефакт. Но можно обратиться к методу Chetan Jags, который позволяет уменьшить проявление артефакта. Для этого на стадии предварительной свертки выборку из карты окружения осуществлять не напрямую, а с одного из её мип-уровней, на основе величины, полученной из функции распределения вероятности подынтегрального выражения и шероховатости:

float D   = DistributionGGX(NdotH, roughness);
float pdf = (D * NdotH / (4.0 * HdotV)) + 0.0001; 

// разрешение для каждой грани исходной кубической карты
float resolution = 512.0;
float saTexel  = 4.0 * PI / (6.0 * resolution * resolution);
float saSample = 1.0 / (float(SAMPLE_COUNT) * pdf + 0.0001);

float mipLevel = roughness == 0.0 ? 0.0 : 0.5 * log2(saSample / saTexel);

Только не забудьте включить трилинейную фильтрацию для карты окружения, чтобы успешно осуществлять выборку из мип-уровней:

glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);

Также не забудьте создать непосредственно мип-уровни для текстуры силами OpenGL, но только после того, как основной мип-уровень полностью сформирован:


// преобразование HDR равнопрямоугольной карты окружения в кубическую карту...
[...]
// создание мип-уровней
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

Данный способ работает на удивление хорошо, убирая практически все (а зачастую и все) пятнав отфильтрованной карте, даже на высоких уровнях шероховатости.

Предварительный расчет BRDF

Итак, мы успешно обработали фильтром карту окружения и теперь можем сконцентироваться на второй части аппроксимации в виде раздельной суммы, представляющей собой BRDF. Для освежения памяти снова взглянем на полную запись приближенного решения:

$L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i$

Левую часть суммы мы предварительно рассчитали и результаты для различных уровней шероховатости записали в отдельную кубическую карту. Правая часть потребует свертки выражения BDRF вместе со следующими параметрами: углом $n \cdot \omega_i$ , шероховатостью поверхности и коэффициентом Френеля $F_0$ . Процесс похожий на интегрирование зеркальной BRDF для полностью белого окружения или с постоянной энергетической яркостью $L_i = 1.0$ . Свертка BRDF для трех переменных является нетривиальной задачей, но в данном случае $F_0$ можно вынести из выражения, описывающего зеркальную BRDF:

$\int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) \frac{F(\omega_o, h)}{F(\omega_o, h)} n \cdot \omega_i d\omega_i$

Здесь $F$ — функция, описывающая расчет к-та Френеля. Перенеся делитель в выражение для BRDF можно перейти к следующей эквивалентной записи:

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} F(\omega_o, h) n \cdot \omega_i d\omega_i$

Заменяя правое вхождение $F$ на аппроксимацию Френеля-Шлика, получим:

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0){(1 - \omega_o \cdot h)}^5) n \cdot \omega_i d\omega_i$

Обозначим выражение ${(1 - \omega_o \cdot h)}^5$ как $/alpha$ для упрощения решения относительно $F_0$ :

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0)\alpha) n \cdot \omega_i d\omega_i$

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + 1*\alpha - F_0*\alpha) n \cdot \omega_i d\omega_i$

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha) + \alpha) n \cdot \omega_i d\omega_i$

Далее функцию $F$ мы разобьем на два интеграла:

$\int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha)) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (\alpha) n \cdot \omega_i d\omega_i$

Таким образом $F_0$ будет постоянной под интегралом, и мы ее можем вынести за знак интеграла. Далее, мы раскроем © Habrahabr.ru