[Перевод] Красивый двоичный поиск без ветвления02.05.2023 10:16

ihfsh5spbj5c7w3z_upbxj-pkvc.png


Недавно я прочитал пост Алекса Мускара Beautiful Binary Search in D. В нём описывается алгоритм двоичного поиска под названием «алгоритм Шора». Я никогда не слышал о нём и его невозможно загуглить, но увидев алгоритм, я думал только об одном: «он без ветвления». Кто знал, что может существовать двоичный поиск без ветвления? Поэтому я занялся его трансляцией в алгоритм для итераторов C++, не требующий индексации на основе единицы или массивов фиксированного размера.

В GCC он более чем в два раза быстрее, чем std: lower_bound, который сам по себе — очень высококачественный двоичный поиск. Цикл поиска прост, а генерируемый ассемблерный код красив. Меня потрясло, что он существует, но им, похоже, никто не пользуется.
Давайте начнём с кода: 

template
It branchless_lower_bound(It begin, It end, const T & value, Cmp && compare)
{
    size_t length = end - begin;
    if (length == 0)
        return end;
    size_t step = bit_floor(length);
    if (step != length && compare(begin[step], value))
    {
        length -= step + 1;
        if (length == 0)
            return end;
        step = bit_ceil(length);
        begin = end - step;
    }
    for (step /= 2; step != 0; step /= 2)
    {
        if (compare(begin[step], value))
            begin += step;
    }
    return begin + compare(*begin, value);
}
template
It branchless_lower_bound(It begin, It end, const T & value)
{
    return branchless_lower_bound(begin, end, value, std::less<>{});
}


Я сказал, что цикл поиска прост, однако, к сожалению, не так просты строки 4–15. Давайте пока их пропустим. Основная часть работы выполняется в строках с 16–20.

Без ветвления


Возможно, цикл не выглядит так, как будто в нём отсутствует ветвление, потому что я очевидно сделал цикл условным, и в теле цикла есть конструкция if. Позвольте мне обосновать это:

  • Конструкция if будет скомпилирована в команду CMOV (условное копирование), то есть ветвление отсутствует. По крайней мере, так делает GCC. Мне не удалось заставить Clang сделать этот код таким, чтобы в нём отсутствовало ветвление, какие бы хитрости я ни пробовал. Поэтому я решил не умничать, потому что для GCC это сработало. Мне бы хотелось, чтобы C++ просто позволил использовать непосредственно CMOV
  • Условие цикла — это ветвление, но оно зависит только от длины массива. Поэтому его очень хорошо можно предсказывать и нам не нужно о нём беспокоиться. В посте Алекса цикл полностью развёртывается, благодаря чему ветвление пропадает, но в моих бенчмарках развёртывание оказалось медленнее, потому что тело функции оказывалось слишком большим для встраивания. Так что я оставил это без изменений.


Алгоритм


Итак, после того, как мы объяснили, что заголовок означает исчезновение одного ветвления и практически бесплатное второе, которое при необходимости можно убрать, давайте расскажем, как всё это работает.

Важной переменной здесь становится step из строки 7. Мы будем совершать скачки с шагом степеней двойки. Если массив имеет длину 64 элемента, то у нас будут значения 64, 32, 16, 8, 4, 2, 1. Он инициализируется ближайшей меньшей степенью двойки от длины входных данных. Поэтому если входные данные имеют длину 22 элемента, то значение будет равно 16. В моём компиляторе нет новой функции std: bit_floor, поэтому я написал собственную для округления до ближайшей степени двойки. После расширения поддержки C++20 её нужно будет заменить вызовом std: bit_floor.

Мы всегда будем выполнять шаги размером в степени двойки, но это станет проблемой, если длина входных данных не равна степени двойки. Поэтому в строках 8–15 мы проверяем, меньше ли середина искомого значения. Если это так, то поиск будет выполняться среди последних элементов. Например: если входные данные имеют длину 22, и это булево значение ложно, то мы выполняем поиск в первых 16 элементах с индекса 0 по 15. Если условная конструкция истинна, мы выполняем поиск в последних восьми элементах с индекса 14 по 21.

input          0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
line 8 compare                                       16
when false     0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
when true                                      14 15 16 17 18 19 20 21


Да, это означает, что индексы 14, 15 и 16 включаются во вторую часть, хотя мы уже исключили сравнением в строке 8, но такова цена удобного цикла. Нам приходится округлять до степени двойки.

Производительность


Какова производительность этого кода? В GCC он невероятно быстр:

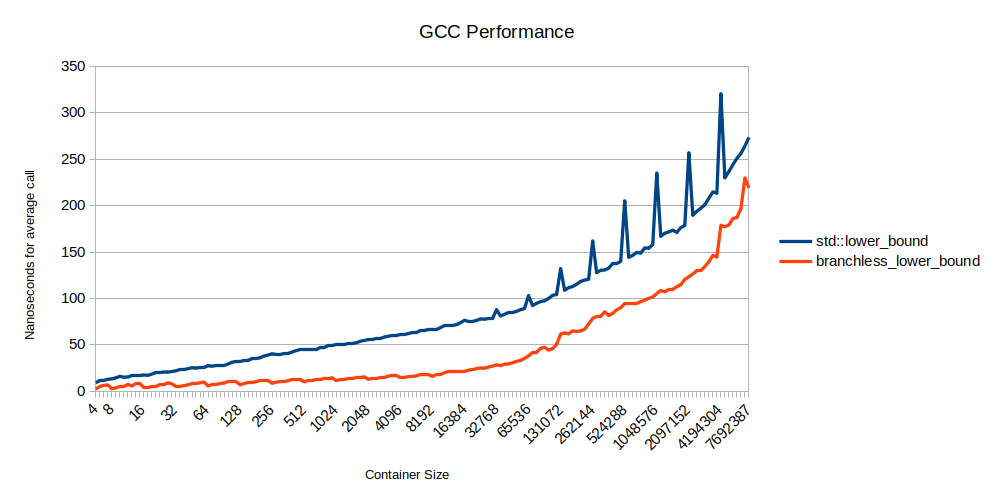
9t0o-t-skiu9rciuumcwziytpt8.png


Примерно при 16 тысячах элементов в массиве он в три раза быстрее std: lower_bound. Дальше начинает доминировать влияние кэша, поэтому уменьшение промахов ветвления менее важно.

Всплески для std: lower_bound происходят в степенях двойки, которые почему-то намного медленнее. Я немного изучил вопрос, но не смог найти простого объяснения. В версии Clang присутствуют точно такие же всплески, хотя алгоритм компилируется в сильно отличающийся ассемблерный код.

То, что в Clang branchless_lower_bound медленнее std: lower_bound, вызвано тем, что мне не удалось избавиться в нём от ветвления:

qo0zp_rkthkha7b8dgkg5yn3ypm.png


Забавно то, что Clang компилирует std: lower_bound так, что ветвление пропадает. Поэтому std: lower_bound быстрее в Clang, чем в GCC, а моя branchless_lower_bound оказывается с ветвлением. Не только красная линия поднимается, но и синяя опускается.

Но это значит, что если мы сравним версию std: lower_bound Clang с версией branchless_lower_bound GCC, то мы будем сравнивать два алгоритма без ветвления. Давайте это сделаем:

ihfsh5spbj5c7w3z_upbxj-pkvc.png


Версия branchless_lower_bound без ветвления быстрее, чем версия std: lower_bound без ветвления. В левой части графика, где массивы меньше, она в среднем быстрее в полтора раза. Почему? В основном из-за сплошного внутреннего цикла. Вот ассемблерный код двух версий:
Это довольно малозатратные операции лишь с небольшой долей параллелизма на уровне команд (каждая итерация цикла зависит от предыдущей, поэтому в обоих случаях количество команд на такт мало), так что мы можем оценить затраты на них, просто их посчитав. Разница между 13 и 5 — это серьёзно. Особенно важны два различия:

  1. branchless_lower_bound должна отслеживать только один указатель вместо одного
  2. std: lower_bound должна заново вычислять размер после каждой итерации. В branchless_lower_bound размер следующей итерации не зависит от предыдущей


Это замечательно, однако функция сравнения передаётся пользователем, и если она гораздо больше, то может получиться гораздо больше циклов, чем у нас есть. В таком случае branchless_lower_bound будет медленнее std: lower_bound. Вот двоичный поиск для строк, который становится всё более затратным при увеличении контейнера:

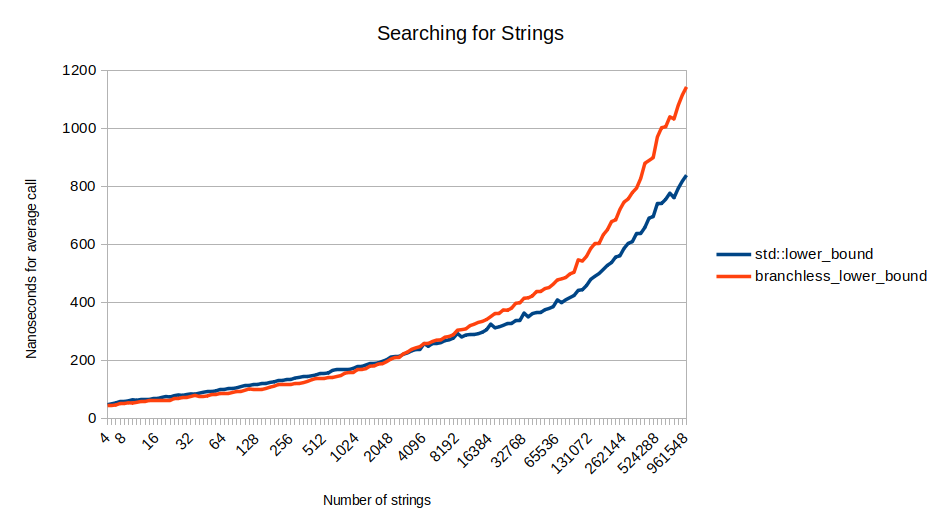
o6mlmby_hejplsgebqf93zyilas.png


Больше сравнений


Почему она медленнее для строк? Потому что выполняет больше сравнений, чем std: lower_bound. Разделение на степени двойки на самом деле неидеально. Например, если входными данными окажется массив [0, 1, 2, 3, 4], и мы будем искать среднее, то есть элемент 2, то функция будет вести себя довольно плохо:
То есть мы выполняем четыре сравнения, когда std: lower_bound требуется только два. Я выбрал пример, в котором ситуация особенно неудобная, мы начинаем с середины и сравниваем один и тот же индекс дважды. Похоже, это можно улучшить, но когда я пытался это сделать, алгоритм становился только медленнее.

Но это будет не сильно хуже идеального двоичного поиска. Для массива из менее чем $2^n$ элементов

— идеальный двоичный поиск использует $n$ или меньше сравнений

— branchless_lower_bound использует $(n+1)$ или меньше сравнений.

В целом оно того стоит: Мы выполняем больше итераций, но выполняем их настолько проворно, что в результате это оказывается гораздо быстрее. Нам лишь нужно помнить о том, что если функция сравнения затратна, то std: lower_bound может быть более правильным выбором.

Ищем источник


В начале статьи я сказал, что алгоритм Шора (Shar«s algorithm) невозможно загуглить. Алекс Мускар написал, что прочитал о нём в книге, написанной в 1982 Джоном Бентли. К счастью, эту книгу можно позаимствовать из Internet Archive. Бентли приводит исходный код и сообщает, что идея взята из «Sorting and Searching» Кнута. Кнут не приводит исходный код. В своей книге он лишь набросал черновик идеи и сообщил, что взял её у Леонарда Шора в 1971 году. Не знаю, где Шор записал свою идею. Возможно, он просто рассказал её Кнуту.

Я уже во второй раз нахожу потрясающий алгоритм из книг Кнута, который стоит использовать активнее, но который почему-то оказался забыт. Возможно, мне стоит внимательно прочитать книгу, чтобы понять, какие идеи хороши, а какие плохи. Например, сразу после изложения алгоритма Шора Кнут гораздо больше времени уделяет рассмотрению двоичного поиска на основании последовательности Фибоначчи. Он быстрее, если нельзя быстро делить целые числа на 2 и можно пользоваться лишь сложением и вычитанием. Поэтому, вероятно, он бесполезен, но кто знает? При чтении книги Кнута приходится предполагать, что большинство алгоритмов бесполезно, и что всё хорошее уже кем-то найдено. К счастью для людей вроде меня, скрытые сокровища по-прежнему можно обнаружить.

Код


Код выложен здесь. Он выпущен под лицензией Boost.

© Habrahabr.ru