[Перевод] Компьютерный поиск помог разобраться с 90-летней математической задачей
Переведя гипотезу Келлера на понятный компьютерам язык поиска в графах, исследователи, наконец, решили задачу покрытия пространств плиткой

Команда математиков, наконец, разобралась с гипотезой Келлера — однако не своими силами. Вместо этого они обучили целый парк компьютеров, и те решили её.
Гипотеза Келлера, выдвинутая 90 лет назад Отт-Генрихом Келлером, связана с задачей покрытия пространств идентичными плитками. Она утверждает, что если замостить двумерное пространство двумерными квадратными плитками, то хотя две из них должны будут соприкасаться сторонами. То же предсказание гипотеза делает для любых измерений — то есть, при заполнении 12-мерного пространства 12-мерными «квадратами», хотя бы у двух из них должна будет найтись общая сторона.
Годами математики бились над этой гипотезой, доказывая её истинность для одних измерений и ложность для других. И к прошлой осени вопрос оставался нерешённым только для семимерного пространства.
Но новое доказательство, созданное компьютером, разрешило и эту проблему. Доказательство, опубликованное в прошлом октябре — это один из новейших примеров комбинации человеческого гения и чистой вычислительной мощности, способных дать ответы на самые волнующие вопросы математики.
Авторы новой работы, Джошуа Брейкенсик из Стэнфорда, Марийн Хиюл и Джон Мэки из университета Карнеги-Меллона, и Дэвид Нарваез из Рочестерского технологического института, решили эту задачу при помощи 40 компьютеров. Всего за 30 минут машины выдали односложный ответ: да, в семи измерениях гипотеза верна. И нам даже не надо принимать это заключение на веру.
К ответу прилагается длинное доказательство, объясняющее его истинность. Доказательство слишком пространно, чтобы его мог понять человек, однако его может проверить другая компьютерная программа.
Иначе говоря, даже если мы не знаем, что именно компьютеры сделали, чтобы доказать гипотез Келлера, мы хотя бы можем убедиться, что сделали они это верно.
Загадочное седьмое измерение
Легко видеть, что в двух измерениях гипотеза Келлера верна. Возьмите листок бумаги и попробуйте покрыть его одинаковыми квадратами без промежутков и без наложения. Довольно скоро вы поймёте, что сделать это удастся, только если хотя бы у двух квадратов будет одна и та же сторона. Если у вас под рукой есть кубики, вам будет легко убедиться, что гипотеза истинна и для третьего измерения. В 1930-м Келлер предположил, что это соотношение работает для всех измерений и соответствующих им плиток.
Ранние результаты поддержали предсказание Келлера. В 1940-м Оскар Перрон доказал, что гипотеза верна для измерений с первого по шестое. Однако более 50 лет спустя новое поколение математиков нашло первый контрпример для этой гипотезы: в 1992 году Джеффри Лагариас и Питер Шор доказали, что гипотеза не работает в 10-м измерении.

Гипотеза Келлера предсказывает, что при заполнении пространства в любом измерении хотя бы две плитки должны полностью соприкасаться сторонами.
При заполнении двумерного пространства у многих плиток находятся общие стороны (синие линии).
При заполнении трёхмерного пространства у многих кубов находятся общие грани (синие).
Легко показать, что если гипотеза не выполняется в каком-то измерении, она не выполняется и во всех старших. Поэтому после работы Лагариаса и Шора осталось только решить вопрос для седьмого, восьмого и девятого измерения. В 2002 году Мэки доказал, что гипотеза Келлера ложна для измерения восемь (и, следовательно, девять).
Открытым осталось только седьмое измерение — это было либо самое большое измерение, для которого эта гипотеза верна, или самое малое, в котором гипотеза неверна.
«Никто точно не знает, что там происходит», — сказал Хиюл.
Соединяем точки
Пока математики бились над этой задачей несколько десятилетий, их методы постепенно менялись. Перрон работал над первыми шестью измерениями, используя лишь карандаш и бумагу, но к 1990-м исследователи придумали, как переводить гипотезу Келлера в совершенно другой вид — позволяющий им применять для её решения компьютеры.
Оригинальная формулировка гипотезы Келлера касается гладкого непрерывного пространства. В таком пространстве существует бесконечное число способов размещения бесконечного количества плиток. Но компьютеры плохо справляются с решением задач, имеющих бесконечное количество вариантов — чтобы справиться с ними, им нужны дискретные и конечные объекты.

Марийн Хиюл из университета Карнеги-Меллона
В 1990 году Кересцтели Корради и Сандор Шабо придумали подходящий дискретный объект. Они показали, что касательно этого объекта можно задавать вопросы, эквивалентные гипотезе Келлера. И если доказать что-то, связанное с этими объектами, то будет доказана и гипотеза Келлера. Это свело вопрос о бесконечности к менее сложной арифметической проблеме с несколькими числами.
Вот, как это работает.
Допустим, вы хотите разобраться с гипотезой Келлера в двух измерениях. Корради и Шабо придумали для этого метод, использующий построение конструкции, которую они назвали графом Келлера.
Для начала представьте, что на столе лежит 16 игральных кубиков, и у всех верхняя грань с двумя точками (две точки обозначают двумерное пространство, а почему кубиков 16 — увидим чуть позже). Все кубики повёрнуты одинаково, так, что две точки расположены однообразно у всех. Раскрасьте каждую точку любым из четырёх цветов: красным, зелёным, белым или чёрным.
Точки на одном кубике не меняются местами — пусть одна из них обозначает координату х, а другая — у. Раскрасив кубики, начнём проводить линии, или рёбра, между парами кубиков при выполнении двух условий: точки в одном и том же месте у пары кубиков имеют разные цвета, а в другом — разные и парные, причём парами считаются красный с зелёным цветом, или чёрный с белым.
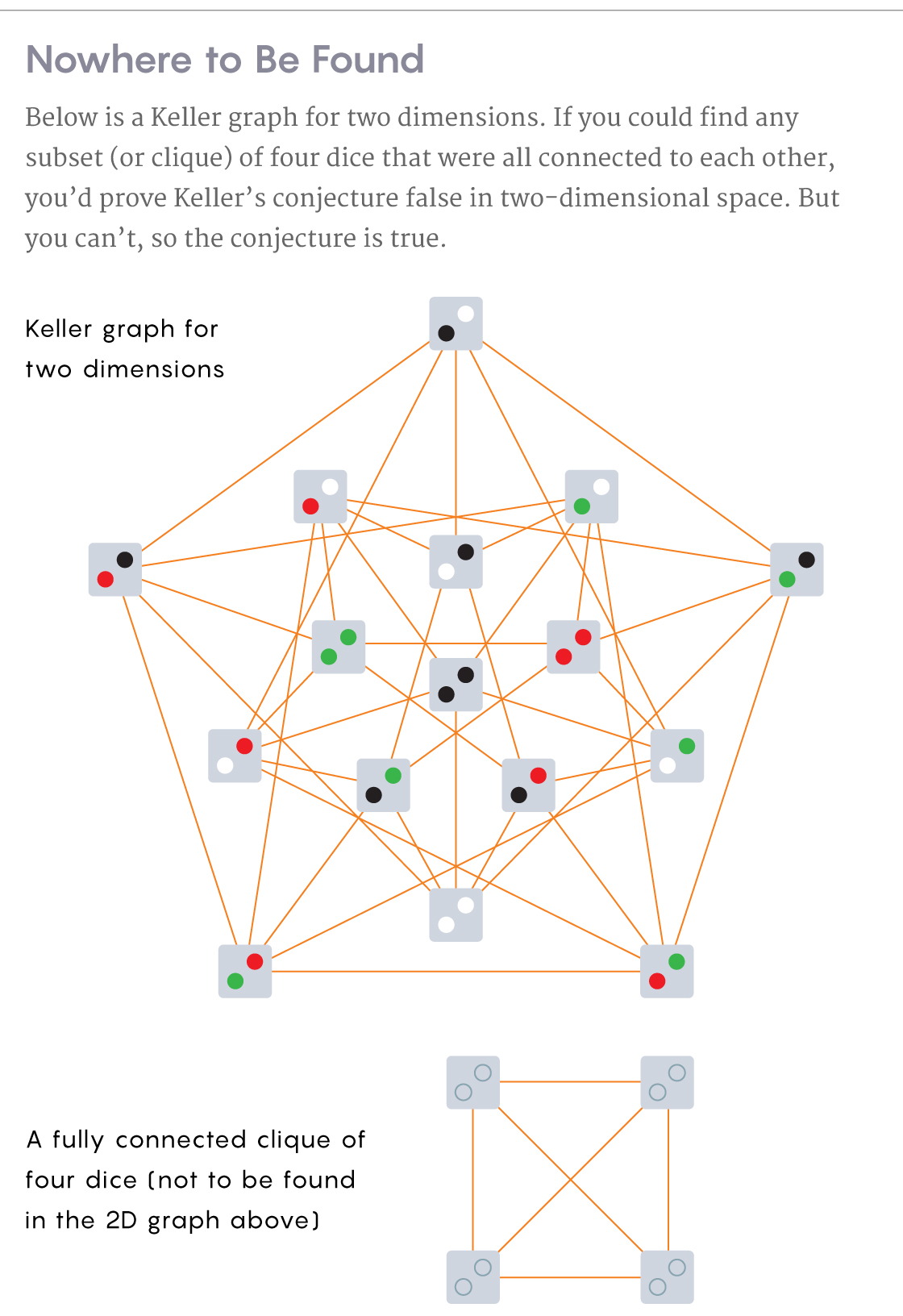
Граф Келлера для двух измерений. Найдя подмножество из четырёх кубиков, в котором каждый соединён со всеми остальными, вы опровергнете гипотезу Келлера для двумерного пространства. Однако такого подмножества нет, и гипотеза верна.
Внизу приведён пример полностью объединённой клики из четырёх кубиков, которой нет в графе.
То есть, к примеру, если у одного кубика две красные точки, а у другого — две чёрные, они не соединяются ребром. Их точки на одинаковых позициях имеют разные цвета, но они не удовлетворяют требованию парности цветов. Если же у одного кубика точки красная и чёрная, а у другого — две зелёных, они соединяются ребром, поскольку в одной позиции у них парные цвета (красный и зелёный), а в другой — просто разные (чёрный и зелёный).
Существует 16 способов раскрасить две точки четырьмя цветами (поэтому у нас 16 кубиков). Разложите все эти 16 возможностей перед собой. Соедините все пары кубиков, удовлетворяющие требованиям. Найдутся ли в вашей схеме четыре кубика, каждый из которых объединён с тремя другими?
Такое полностью связанное подмножество кубиков называется кликой. Если вы сможете найти такую, вы опровергнете гипотезу Келлера в двух измерениях. Однако вы не сможете — её просто не существует. А отсутствие такой клики из четырёх кубиков означает, что гипотеза Келлера верна для двух измерений.
Эти кубики не являются буквально теми плитками, о которых говорится в гипотезе Келлера, однако вы можете считать, что каждый кубик представляет плитку. Цвета, назначенные точкам, считайте координатами, располагающими кубик в пространстве. А существование ребра — описанием того, как два кубика располагаются относительно друг друга.
Если цвета кубиков одинаковые, они представляют плитки, одинаково расположенные в пространстве. Если у них нет общих цветов и пар цветов (у одного чёрный и белый цвета, у другого — зелёный и красный), они обозначают частично накладывающиеся плитки — что в заполнении пространства не разрешается. Если у двух кубиков один набор парных цветов и один набор одного цвета (один красно-чёрный, другой зелёно-чёрный), они обозначают плитки с общей стороной.
Наконец, что наиболее важно — если у них один набор парных цветов и другой набор разных цветов — то есть, если они соединяются ребром — то кубики обозначают плитки, соприкасающиеся друг с другом, но немного сдвинутые, из-за чего их грани не совпадают полностью. Именно это условие нам и нужно изучать. Соединённые ребром кубики обозначают соприкасающиеся плитки, не имеющие общей стороны — именно такое расположение нужно для опровержения гипотезы Келлера.
«Они должны соприкасаться, но не полностью», — сказал Хиюл.

Одинаковая раскраска — одинаковое расположение.
Разные цвета, нет пар — частичное наложение.
Два парных цвета и пара одинаковых — общая сторона.
Два парных цвета и два разных — частичное соприкосновение сторонами.
Масштабирование
Тридцать лет назад Корради и Шабо доказали, что математики могут использовать подобную процедуру для работы с гипотезой Келлера в любом измерении, подправляя параметры эксперимента. Для доказательства гипотезы Келлера в трёх измерениях можно использовать 216 кубиков с тремя точками на грани, и, возможно, три пары цветов (однако тут возможна некоторая гибкость). Потом нужно поискать восемь кубиков (23), полностью соединённых друг с другом, по тем же условиям, что мы приводили выше.
В целом, для доказательства гипотезы Келлера в n измерениях нужно использовать кубики с n точек и попытаться найти среди них клику размера 2n. Можно считать, что она представляет некую сверхплитку (состоящую из 2n плиток меньшего размера), способную покрыть всё n-мерное пространство.
Если вы сможете найти эту сверхплитку (в которой нет плиток с общей стороной), вы сможете использовать её копии для покрытия всего пространства плитками без общей стороны, что опровергнет гипотезу Келлера.
«В случае успеха вы можете покрыть всё пространство переносом. Блок без общих сторон плиток распространится на всё покрытие», — сказал Лагариас, сейчас работающий в Мичиганском университете.
Мэки опроверг гипотезу Келлера в 8-м измерении, найдя клику из 256 кубиков (28), поэтому оставалось разобраться с гипотезой в 7-м измерении, найдя клику из 128 кубиков (27). Найдя эту клику, вы опровергнете гипотезу Келлера в седьмом измерении. Докажите, что она не существует — и вы докажете истинность гипотезы.
К сожалению, поиск клики из 128 кубиков — задача особенно сложная. В предыдущих работах исследователи пользовались тем фактом, что измерения 8 и 10 можно в некотором смысле «разложить» на пространства меньшей размерности, с которыми проще работать. А тут такого не получалось.
«Седьмое измерение неудобное, поскольку 7 — простое число, и на измерения меньшего порядка его не разобьёшь, — сказал Лагариас. — Поэтому не оставалось выхода, кроме как разбираться с полноценной комбинаторикой этих графов».
Для невооружённого мозга поиск клики из 128 кубиков может быть сложной задачей — однако именно на такие вопросы хорошо умеют отвечать компьютеры, особенно если им немного помочь.
Язык логики
Чтобы превратить поиск клик в задачу, с которой справится компьютер, нужно сформулировать её в терминах логики высказываний. Это такие логические рассуждения, в которые входит набор ограничений.
Допустим вы втроём с друзьями планируете вечеринку. Вы пытаетесь составить список гостей, однако в нём встречаются столкновения интересов. Допустим, вы хотите либо пригласить Алексея, либо исключить Колю. Один из ваших друзей хочет пригласить Колю, или Влада, или их обоих. Другой друг не хочет звать ни Алексея, ни Влада. Можно ли с такими ограничениями составить список гостей, который удовлетворит всех троих?
В терминах информатики эта задача называется задачей на приемлемость. Решить её можно, описав условие в пропозициональной формуле. В данном случае она имеет следующий вид, а А, К и В обозначают потенциальных гостей: (A OR NOT K) AND (K OR B) AND (NOT A OR NOT B).
Компьютер просчитывает её, подставляя в каждую переменную 0 или 1. 0 — значение переменной «ложь», или выключено, а 1 — «правда» или включено. Подставив 0 вместо А, мы говорим о том, что Алексея не пригласили, а 1 — что пригласили. В эту простую формулу 0 и 1 можно подставить (составляя список гостей) множеством способов, и, возможно, что после перебора их всех компьютер заключит, что всем интересам удовлетворить невозможно. Однако в данном случае есть два способа подставить 1 и 0 так, чтобы всем угодить: A = 1, K = 1, B = 0 (пригласить Алексея и Колю) и A = 0, K = 0, B = 1 (пригласить одного Влада).
Компьютерная программа, решающая такие утверждения, называется SAT solver, где SAT — сокращение от satisfiability, «удовлетворяемость». Она исследует все комбинации переменных и выдаёт односложный ответ — либо ДА, есть способ удовлетворить требованиям формулы, либо НЕТ, его нет.

Джон Маки из университета Карнеги-Меллона
«Вы просто смотрите, можно ли назначить всем переменным значения правда и ложь так, чтобы вся формула была истинной, и если да, то она удовлетворяема, а если нет — то нет», — сказал Томас Хейлс из Питтсбургского университета.
Вопрос поиска клики из 128 кубиков — задача сходного толка. Её тоже можно переписать в виде пропозициональной формулы и задать SAT-солверу. Начните с большого количества кубиков с 7 точками на каждом и шестью возможными цветами. Можно ли раскрасить точки так, чтобы 128 кубиков были связаны друг с другом по определённым правилам? Иначе говоря, можно ли назначить цвета так, чтобы клика появилась?
Пропозициональная формула, описывающая вопрос с кликами, получилась довольно длинной и содержит 39 000 переменных. Каждой можно назначить одно из двух значений, 0 или 1. В итоге количество возможных вариантов расстановки значений, или способов назначения цветов, составило 239 000 — что очень, очень много.
Чтобы найти ответ на вопрос по поводу гипотезы Келлера в семи измерениях, компьютеру пришлось бы проверить все эти комбинации — и либо исключить их все (что означало бы, что клики размера 128 не существует, и гипотеза Келлера в седьмом измерении верна), либо найти хотя бы один рабочий вариант (опровергнув гипотезу Келлера).
«Если провести простой перебор всех возможностей, вы столкнётесь с 324-значным числом», — сказал Мэки. Самый быстрый компьютер в мире работал бы до конца времён, перебирая все возможности.
Однако авторы новой работы придумали, как компьютер может выдать определённы ответ, не проверяя все возможности. Ключ к этому — эффективность.
Скрытые эффективности
Мэки вспоминает тот день, когда, с его точки зрения, проект реально заработал. Он стоял перед доской в своём офисе в университете Карнеги-Меллона, обсуждая проблему с двумя соавторами, Хиюлом и Брейкенсиком, когда Хиюл предложил способ структурировать поиск так, чтобы его можно было закончить за разумное время.
«В тот день в моём офисе реально работал человеческий гений, — сказал Мэки. — Я будто наблюдал за Уэйном Гретцки, или за Леброном Джеймсом в финале НБА. У меня мурашки по телу от одного только воспоминания об этом».
Подгонять поиски определённого графа Келлера можно разными способами. Представьте, что у вас на столе множество кубиков, и вы пытаетесь собрать 128 из них, удовлетворяя правилам графа Келлера. Допустим, вы правильно отобрали 12, но никак не можете придумать, как добавить следующий. В этот момент вы можете отбросить все конфигурации из 128 кубиков, в которые входит эта нерабочая конфигурация из 12-и.
«Если вы знаете, что первые пять ваших назначений не сочетаются, вам не нужно искать другие переменные, и обычно это сильно урезает поле поиска», — сказал Шор, ныне работающий в MIT.
Ещё один вид эффективности связан с симметрией. Симметричные объекты в какой-то мере одинаковы. Одинаковость позволяет нам понять весь объект целиком, изучая лишь его часть — посмотрев на половину лица человека, можно восстановить его целиком.
Подобным образом срезать углы можно и в случае с графами Келлера. Представьте снова, что вы пытаетесь выстроить кубики на столе. Допустим, вы начинаете с центра стола и выстраиваете комбинацию слева. Вы выкладываете четыре кубика, и заходите в тупик. Теперь вы исключили одну начальную комбинацию и все комбинации, основанные на ней. Однако вы можете исключить и зеркальное отражение этой начальной комбинации — конфигурацию кубиков, которую вы получите, если разместите их таким же образом, только справа.
«Если вы придумали способ решения удовлетворяемых задач, умным образом учитывающий симметрию, вы серьёзно упростили задачу», — сказал Хейлс.
Четверо коллег воспользовались преимуществом эффективностей подобного поиска новым способом — в частности, они автоматизировали рассмотрение симметричных случаев, в то время как ранее математики обрабатывали их практически вручную.
В итоге они настолько улучшили поиски клики размера 128, что вместо проверки 239 000 конфигураций их программе пришлось проверять всего порядка миллиарда (230). Это превратило поиск, на который могла уйти вечность, в задачку на одно утро. Наконец, всего через полчаса вычислений они получили ответ.
«Компьютеры сказали 'нет', поэтому мы знаем, что гипотеза работает», — сказал Хиюл. Невозможно раскрасить 128 кубиков так, чтобы они все объединились друг с другом, поэтому гипотеза Келлера для седьмого измерения подтверждается. При любом размещении плиток, покрывающих пространство, неизбежно найдётся хотя бы пара, полностью соприкасающаяся гранями.
Компьютер выдал не просто односложный ответ. Он присовокупил к нему длинное доказательство на 200 ГБ, поддерживающее это заключение.
Доказательство — не просто выкладках всех наборов переменных, проверенных компьютером. Это логическая аргументация, доказывающая, что необходимой клики существовать не может. Исследователи скормили доказательство в программу, проверяющую формальные доказательства через отслеживание логики аргумента, и подтвердили его.
«Мы не просто перебрали все варианты и ничего не нашли. Мы перебрали все варианты и смогли записать доказательство, что такой штуки не существует, — сказал Мэки. — Мы смогли записать доказательство неудовлетворяемости».
