[Перевод] Кластерный анализ (на примере сегментации потребителей) часть 1
Мы знаем, что Земля — это одна из 8 планет, которые вращаются вокруг Солнца. Солнце — это всего лишь звезда среди порядка 200 миллиардов звезд в галактике Млечный Путь. Очень тяжело осознать это число. Зная это, можно сделать предположение о количестве звезд во вселенной — приблизительно 4×10^22. Мы можем видеть около миллиона звезд на небе, хотя это всего лишь малая часть от всего фактического количества звезд. Итак, у нас появилось два вопроса: Что такое галактика?
И какая связь между галактиками и темой статьи (кластерный анализ)
Галактика — это скопление звезд, газа, пыли, планет и межзвездных облаков. Обычно галактики напоминают спиральную или эдептическую фигуру. В пространстве галактики отделены друг от друга. Огромные черные дыры чаще всего являются центрами большинства галактик.Как мы будем обсуждать в следующем разделе, есть много общего между галактиками и кластерным анализом. Галактики существуют в трехмерном пространстве, кластерный анализ — это многомерный анализ, проводимый в n-мерном пространстве.
Заметка: Черная дыра — это центр галактики. Мы будем использовать похожую идею в отношении центроидов для кластерного анализа.
Кластерный анализПредположим вы глава отдела по маркетингу и взаимодействию с потребителями в телекоммуникационной компании. Вы понимаете, что все потребители разные, и что вам необходимы различные стратегии для привлечения различных потребителей. Вы оцените мощь такого инструмента как сегментация клиентов для оптимизации затрат. Для того, чтобы освежить ваши знания кластерного анализа, рассмотрим следующий пример, иллюстрирующий 8 потребителей и среднюю продолжительность их разговоров (локальных и международных). Ниже данные: 
Для лучшего восприятия нарисуем график, где по оси x будет откладываться средняя продолжительность международных разговоров, а по оси y — средняя продолжительность локальных разговоров. Ниже график:
Заметка: Это похоже на анализ расположения звезд на ночном небе (здесь звезды заменены потребителями). В дополнение, вместо трехмерного пространства у нас двумерное, заданное продолжительностью локальных и международных разговоров, в качестве осей x и y.Сейчас, разговаривая в терминах галактик, задача формулируется так — найти положение черных дыр; в кластерном анализе они называются центроидами. Для обнаружения центроидов мы начнем с того, что возьмем произвольные точки в качестве положения центроидов.
Евклидово расстояние для нахождения Центроидов для Кластеров
В нашем случае два центроида (C1 и C2) мы произвольным образом поместим в точки с координатами (1, 1) и (3, 4). Почему мы выбрали именно эти два центроида? Визуальное отображение точек на графике показывает нам, что есть два кластера, которые мы будем анализировать. Однако, впоследствии мы увидим, что ответ на этот вопрос будет не таким уж простым для большого набора данных.Далее, мы измерим расстояние между центроидами (C1 и C2) и всеми точками на графике использую формулу Евклида для нахождения расстояния между двумя точками.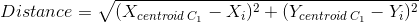
Примечание: Расстояние может быть вычислено и по другим формулам, например,
квадрат евклидова расстояния — для придания веса более отдаленным друг от друга объектам
манхэттенское расстояние — для уменьшения влияния выбросов
степенное расстояние — для увеличения/уменьшения влияния по конкретным координатам
процент несогласия — для категориальных данных
и др.
Колонка 3 и 4 (Distance from C1 and C2) и есть расстояние, вычисленное по этой формуле. Например, для первого потребителя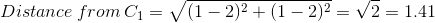
Принадлежность к центроидам (последняя колонка) вычисляется по принципу близости к центроидам (C1 и C2). Первый потребитель ближе к центроиду №1 (1.41 по сравнению с 2.24) следовательно, принадлежит к кластеру с центроидом C1.
Ниже график, иллюстрирующий центроиды C1 и C2 (изображенные в виде голубого и оранжевого ромбика). Потребители изображены цветом соответствующего центроида, к кластеру которого они были отнесены.
Так как мы произвольным образом выбрали центроиды, вторым шагом мы сделать этот выбор итеративным. Новая позиция центроидов выбирается как средняя для точек соответствующего кластера. Так, например, для первого центроида (это потребители 1, 2 и 3). Следовательно, новая координата x для центроида C1 э то средняя координат x этих потребителей (2+1+1)/3 = 1.33. Мы получим новые координаты для C1 (1.33, 2.33) и C2 (4.4, 4.2).Новый график ниже:
В конце концов, мы поместим центроиды в центр соответствующего кластера. График ниже:
Позиции наших черных дыр (центров кластеров) в нашем примере C1 (1.75, 2.25) и C2(4.75, 4.75). Два кластера выше подобны двум галактикам, разделенным в пространстве друг от друга.
Итак, рассмотрим примеры дальше. Пусть перед нами стоит задача по сегментации потребителей по двум параметрам: возраст и доход. Предположим, что у нас есть 2 потребителя с возрастом 37 и 44 лет и доходом в $90,000 и $62,000 соответственно. Если мы хотим измерить Евклидово расстояние между точками (37, 90000) и (44, 62000), мы увидим, что в данном случае переменная доход «доминирует» над переменной возраст и ее изменение сильно сказывается на расстоянии. Нам необходима какая-нибудь стратегия для решения данной проблемы, иначе наш анализ даст неверный результат. Решение данной проблемы это приведение наших значений к сравнимым шкалам. Нормализация — вот решение нашей проблемы.
Нормализация данных
Существует много подходов для нормализации данных. Например, нормализация минимума-максимума. Для данной нормализации используется следующая формула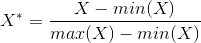
в данном случае X* — это нормализованное значение, min и max — минимальная и максимальная координата по всему множеству X (Примечание, данная формула располагает все координаты на отрезке [0;1])Рассмотрим наш пример, пусть максимальный доход $130000, а минимальный — $45000. Нормализованное значение дохода для потребителя A равно
Мы сделаем это упражнение для всех точек для каждых переменных (координат). Доход для второго потребителя (62000) станет 0.2 после процедуры нормализации. Дополнительно, пусть минимальный и максимальный возрасты 23 и 58 соответственно. После нормализации возрасты двух наших потребителей составит 0.4 и 0.6.
Легко увидеть, что теперь все наши данные расположены между значениями 0 и 1. Следовательно, у нас теперь есть нормализованные наборы данных в сравнимых шкалах.
Запомните, перед процедурой кластерного анализа необходимо произвести нормализацию.
Статью нашел kuznetsovin
