[Перевод] Кем был Рамануджан?
Перевод поста Stephen Wolfram «Who Was Ramanujan?».
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
Содержание
Удивительное письмо
Начало истории
Кем был Харди?
Письмо и его последствия
Стиль работы Рамануджана
Видеть то, что важно
Истина или объяснение
Переход в Кембридж
Рамануджан в Кембридже
Что было дальше
Что стало с Харди?
Математика Рамануджана
Факты — случайные или нет?
Автоматизация работ Рамануджана
Современные Рамануджаны?
Что было бы, если бы у Рамануджана была Mathematica? На этой неделе вышел фильм «Человек, который познал бесконечность» (который мне показали еще прошлой осенью Манджул Бхаргава и Кен Оно), так что я не мог не написать о его главном герое — Сринивасе Рамануджане.
Удивительное письмо
Раньше они приходили по обычной почте. Сейчас — по электронной. В течение многих лет со всего мира ко мне стекаются письма, в которых содержатся смелые утверждения о простых числах, теории относительности, искусственном интеллекте, сознании и множестве других вещей. Глядя на эти сообщения, я вспоминаю историю Рамануджана и неизменно откладываю свои идеи и проекты, чтобы хотя бы просмотреть их.
Около 31 января 1913 года математик по имени Харди из Кембриджа, Англия, получил пакет документов с сопроводительным письмом, которое начиналось так:»Дорогой сэр, хочу представиться вам: я клерк из бухгалтерии порта в Мадрасе с зарплатой £20 в год. Мне 23 года…». И продолжал: писал о том, что достиг «поразительного» прогресса в теории расходящихся рядов по математике и решил давнишнюю проблему распределения простых чисел. Сопроводительное письмо заканчивалось словами:»Я беден; если вы решите, что здесь есть что-нибудь ценное, я хотел бы, чтобы мои теоремы были опубликованы… Я неопытен, и любые ваши советы ценны для меня. Прошу извинить меня за доставленные неудобства. Искренне ваш, с уважением, С. Рамануджан».
Далее следовало по крайней мере 11 страниц технических результатов из целого ряда областей математики (из которых 2 потеряны). Там было абсурдное на первый взгляд утверждение, что сумма всех положительных чисел равна -1/12:
Были утверждения, предполагающие использование своего рода экспериментального подхода в математике:
Были там и более экзотические страницы с формулами вроде этой:
Что это? Откуда они взялись? Правильны ли они?
Сами понятия должны быть хорошо знакомы человеку, изучавшему матанализ в колледже. Однако к письму были приложены не просто сложные упражнения уровня колледжа. Если присмотреться внимательно, на каждой странице письма происходит нечто совершенно необычное и неожиданное, — кажется, это математика другого уровня.
На сегодняшний день для численной проверки результатов мы можем использовать Mathematica или Wolfram | Alpha. А иногда мы можем даже просто ввести вопрос и сразу же получить ответ:
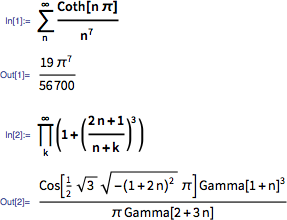
Можно убедиться (как и Г.Х. Харди в 1913 году), что формулы правильные. Однако что за человек мог их вывести? И как? Являются ли они частью более широкой картины или в каком-то смысле просто хаотичными случайными фактами из математики?
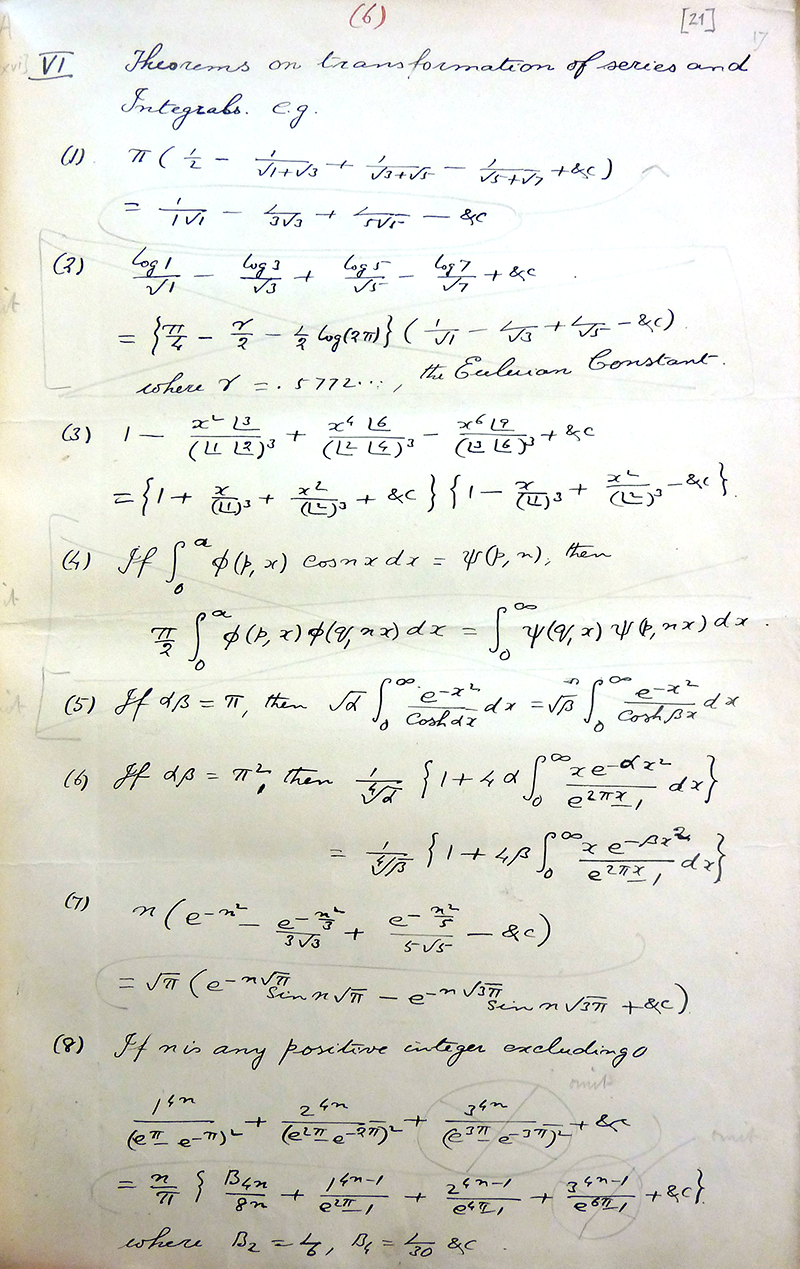
Начало истории
За этим письмом стоит замечательная история Рамануджана.
Он родился в небольшом городке в Индии 22 декабря 1887 г. (это означает, что ему было не «около 23» лет, когда он писал свое письмо Харди, а все 25). Его семья была небогатой и принадлежала к касте браминов (священников, учителей и др.). Уже в 10 лет Рамануджан явно выделялся среди прочих по результатам экзаменов в обновленной системе школьного образования. Он также был известен из-за своей исключительной памяти: он мог декламировать цифры числа пи так же хорошо, как корни санскритских слов. Когда в возрасте 17 лет он закончил среднюю школу, ему дали стипендию для обучения в колледже.
В средней школе Рамануджан начал самостоятельно изучать математику и проводить собственное исследование численной оценки постоянной Эйлера и свойств чисел Бернулли. Ему повезло, что в 16 лет (в те дни, задолго до Интернета!) он получил копию удивительно хорошего и полного (по крайней мере, по состоянию на 1886 г.) конспекта по математике для студентов высшей школы, состоявшего из 1055 страниц! Книга была написана преподавателем трехлетней программы по математике для подготовки к экзаменам в Кембридж, и его скупой формат в стиле «только факты» был очень похож на тот, что Рамануджан использовал в своем письме к Харди.
К тому времени, как Рамануджан поступил в колледж, он хотел заниматься только математикой, и в результате провалил остальные экзамены и сбежал, так что его матери пришлось даже писать в газету письмо о пропавшем без вести:
Рамануджан переехал в Мадрас (теперь Ченнаи), где пробовал учиться в разных колледжах, болел и в результате продолжил свое независимое исследование по математике. В 1909 году, когда ему был 21 год, его мама в соответствии с обычаями того времени договорилась о его свадьбе с 10-летней девочкой по имени Янаки, которая начала жить с ним пару лет спустя.
Рамануджан обеспечивал себя, занимаясь репетиторством по математике, но вскоре он стал известен в окрестностях Мадраса как математик и начал печататься в недавно запущенном Журнале Индийского математического общества. Его первая статья, опубликованная в 1911 году, была посвящена вычислительным свойствам чисел Бернулли (те же числа Бернулли, что Ада Лавлейс (см. статью «Распутывая историю Ады Лавлейс (первого программиста в истории)» на Хабре) использовала в своей статье от 1843 года про аналитическую машину). Хотя его результаты не слишком впечатляли, подход Рамануджана был интересным и оригинальным: в нем сочетались непрерывная («каково численное значение?») и дискретная («какое разложение на простые множители?») математика.
После того, как друзьям-математикам Рамануджана не удается получить ему стипендию, он начинает искать работу, и в марте 1912 года Рамануджан попадает счетоводом в порт Мадрас. Его босс — главный бухгалтер — интересовался академической математикой и стал пожизненным его сторонником. Руководителем порта Мадрас в то время был выдающийся британский инженер-строитель, так что Рамануджан через него начал взаимодействовать с некоторыми британскими экспатриантами. Они рассуждали о том, есть ли у него «способности великого математика» или же он просто «мальчик-калькулятор». Они писали профессору Хилл в Лондон, который посмотрел на ряд диковинных заявлений Рамануджана о расходящихся рядах и заявил, что »г-н Рамануждан, очевидно, человек со вкусом к математике, и даже с некоторыми способностями, но он идет по неверному пути». Хилл предложил Рамануджану изучить некоторые книги.
В то время, как друзья Рамануджана продолжали искать способ поддержать его, он решил сам начать писать британским математикам — пускай и с некоторой помощью при составлении писем на английском языке. Мы не знаем точно, кому он написал первому, хотя давний соратник Харди Джон Литтлвуд незадолго до своей смерти 64 года спустя упомянул два имени: Х.Ф. Бейкер и Е.В. Хобсон. Они оба были не слишком удачным выбором: Бейкер работал в области алгебраической геометрии, а Хобсон занимался математическим анализом: достаточно далеко от того, что делал Рамануджан. В любом случае, ни один из них не ответил.
И вот в четверг, 16 января 1913 года, Рамануждан пишет свое письмо Г.Х. Харди.
Кем был Харди?
Годфри Харолд Харди родился в 1877 году в семье школьных учителей. Жили они примерно в 30 милях к югу от Лондона. С самого начала он был лучшим учеником — особенно в области математики. Даже когда я рос в Англии в начале 1970-х, такие студенты в средней школе обычно переходили в Винчестер, а после шли в Кембридж. Именно это и сделал Харди. Другие были чуть более известными, чуть менее строгими и менее математически ориентированными — это Итон и Оксфорд (в который я поступил).
Студенты кембриджского бакалавриата занимались в то время решением витиевато сконструированных проблем исчисления (это напоминало серьезные спортивные соревнования), а в конце составлялся рейтинг студентов, занимающих в нем позиции от «Senior Wrangler» (наивысший балл) до «Wooden Spoon» (самый низкий проходной балл). Харди думал, что он будет первым на курсе, однако оказался четвертым. Он пришел к выводу, что ему больше по душе строгий и формальный подход к математике, который затем стал популярным в континентальной Европе.
Британская академическая система работала в то время (и до 1960-х годов) таким образом, что после получения высшего образования лучшие студенты могли быть избраны стипендиатами колледжа и получать стипендии даже пожизненно. Харди был в Тринити-колледже — самом большом и лучшем с научной точки зрения колледже в Кембриджском университете, а после его окончания в 1900 году он был избран стипендиатом колледжа.
Темой первой исследовательской работы Харди были интегралы, подобные этим:
В течение десяти лет Харди работал в основном над тонкостями вычисления, выяснял, как брать различные виды интегралов и их сумм, и настаивал на более строгом подходе к вопросам сходимости и перестановки пределов интегрирования.
Его работы не были ни великими, ни провидческими, однако они стали прекрасными примерами математического мастерства. Как и его коллега Бертран Рассел, он начал заниматься вскоре новой областью — трансфинитными числами, однако работает с ними недолго. Затем в 1908 году он написал учебник »Курс чистой математики» — это была хорошая и даже очень успешная в свое время книга (в предисловии к ней говорилось, что учебник предназначался студентам, чьи способности достигают уровня «стандарта стипендиата»).
К 1910 году Харди в погрузился в рутину жизни профессора Кембриджского университета и занимался академической работой. И тогда он познакомился с Джоном Литтлвудом. Литтлвуд вырос в Южной Африке и был на восемь лет моложе Харди, недавний Senior Wrangler и во многих отношениях гораздо более предприимчивый. И в 1911 году Харди, который ранее работал только сам, влился в сотрудничество с Литтлвудом, продолжавшееся остаток его жизни.
Как человек Харди производил впечатление хорошего школьника, который так никогда и не повзрослеет. Казалось, ему нравится жить в структурированной среде, концентрируясь на своих математических упражнениях. Он был очень занудным — касалось ли это подсчета баллов во время игры в крикет, доказательства отсутствия Бога или написания правил для его сотрудничества с Литтлвудом. Будучи типичным британцем, он мог бы самовыражаться с умом и обаянием, однако он был жестким и отчужденным: он даже называл себя «Г.Х. Харди», будучи «Харолдом» только с матерью и сестрой.
Таким образом, к началу 1913 года Харди был респектабельным и успешным британским математиком, заинтересованным в новом сотрудничестве с Литтлвудом, который тянул его в интересующую его область теории чисел. Но потом он получил письмо от Рамануджана.
Письмо и его последствия
Письмо Рамануджана начиналось не слишком удачно: создавалось впечатление, что он думает, что впервые описывает хорошо известную технику аналитического продолжения для обобщения таких идей и понятий, как факториал, на нецелые числа. Он заявил:»я настолько развил эти идеи в своих исследованиях, что местные математики не в состоянии понять меня и мои работы». Однако после сопроводительного письма следовало более девяти страниц, которые содержали более 120 различных математических результатов.
Вначале там были довольно расплывчатые заявления. Но на третьей странице были формулы для сумм и интегралов и прочего. Некоторые из них отдаленно напоминали те, что были в работах Харди. А некоторые из них были определенно более экзотические. Их общая структура была характерна для этих типов математических формул, однако некоторые конкретные формулы удивляли: в них утверждалось, что некоторые вещи математически равны, тогда как нельзя было даже ожидать, чтобы они были связаны между собой.
По крайней мере две страницы оригинального письма пропали без вести. Последняя страница, которая у нас есть, снова, кажется, заканчивается неудачно: Рамануджан, описывая достижения своей теории расходящихся рядов, приходит к, казалось бы, абсурдному результату о том, что сумма всех положительных целых чисел 1 + 2 + 3 + 4 +… равна -1 / 12.
Как отреагировал Харди? Во-первых, он проконсультировался у Литтлвуда. Было ли это письмо розыгрышем? Были ли эти формулы уже известны, или, возможно, совершенно неправильны? Некоторые они опознали. А вот остальные — нет. Харди сказал позже, что и они должны быть правильными,»потому что если бы они не были правдой, никому не хватило бы воображения их придумать».
Бертран Рассел писал, что на следующий день он »нашел Харди и Литтлвуда в состоянии дикого возбуждения, потому что они считают, что нашли второго Ньютона — индуистского клерка, который зарабатывает в Мадрасе 20 фунтов в год». Харди многим людям показал письмо Рамануджана, а затем начал делать запросы правительственным департаментам, управляющим Индией. Все это заняло у него неделю, а затем он написал ответное письмо Рамануджану, в котором ясно читается волнение:»Я был чрезвычайно заинтересован вашим письмом и теоремами, которые вы сформулировали».
Затем он продолжил:»Однако вы должны понять, что, прежде чем я смогу судить правильно о ценности того, что вы сделали, я должен увидеть доказательства некоторых из ваших утверждений». Любопытно, что он сказал это. Для Харди недостаточно было просто знать, что это правда; ему нужны были доказательства. Конечно, Харди мог бы самостоятельно их найти. Однако мне кажется, что отчасти он написал так потому, что хотел получить более полное представление о том, насколько хорошим математиком был Рамануджан.
В своем письме с характерной для него точностью Харди разделил содержимое письма Рамануджана на три категории: то, что уже было известно; новое и интересное, но не очень важное; и, наконец, новое и потенциально важное. Однако единственным, что он отнес к третьей категории, было заявление Рамануджана о подсчете простых чисел, добавив при этом, что »почти все зависит от точности и строгости методов доказательства, которые вы использовали».
Харди, очевидно, сделал к тому моменту некоторые предварительные исследования работ Рамануджана, так как в своем письме он ссылается на его статью, посвященную числам Бернулли. Он пишет:»я очень надеюсь, что вы отправите мне как можно быстрее… некоторые из ваших доказательств», а затем заканчивает словами:»в надежде как можно скорее получить от вас ответ».
Рамануджан действительно быстро отреагировал на письмо Харди. Во-первых, он писал, что он ожидал такого же ответа от Харди, как и от одного »профессора математики в Лондоне», который просто сказал ему »не попадать в ловушку расходящихся рядов». Затем он отвечает на пожелание Харди строгих доказательств, говоря:»если бы я продемонстрировал вам мои методы доказательства, то, уверен, вы присоединились бы к мнению лондонского профессора». Далее он упоминает свой результат
1 + 2 + 3 + 4 +… = -1 / 12,
и добавляет, что »… если я скажу вам, то вы ответите, что мое место — в психушке». И продолжает:»я говорю об этом только для того, чтобы убедить вас, что вы не в состоянии будете следовать моим методам доказательства… основанным на одной букве». Он говорит, что его первая цель состоит в том, чтобы найти кого-то вроде Харди, чтобы проверить свои результаты, а значит, иметь возможность получить стипендию, так как »я уже живу впроголодь. Чтобы сохранить мозги, мне нужна еда…».
Рамануджан заканчивает словами о том, что наличие той первой категории результатов, которые уже известны, очень его обрадовало, потому что »мои результаты верифицируются — в противном случае моя позиция была бы слишком шаткой». Другими словами, Рамануджан и сам не был уверен в правильности полученных результатов, и он был рад, что оказался прав.
Как же он получал свои результаты? Позже я расскажу об этом подробнее. Но он, конечно, делал все виды расчетов с числами и формулами — по сути, занимался экспериментами. И, вероятно, он смотрел на результаты этих вычислений, чтобы понять, какие из них верны. До сих пор неизвестно, как он определял это; к тому же некоторые его результаты в конце концов не выдержали критики. Возможно, он использовал как традиционные приемы математических доказательств и подтверждение с помощью вычислений, так и доверял своей интуиции. Однако ничего из этого он не сказал Харди.
Вместо этого он просто вел с ним переписку о деталях результатов, а также приводил фрагменты доказательств, которые он был в состоянии дать. Казалось, Харди и Литтлвуд намеренно нивелируют его усилия: например, Литтлвуд писал о каких-то его результатах:»(d) — это, конечно, неверно». При этом они оба задавались вопросом, был ли Рамануджан «Эйлером» или просто «Якоби». Однако Литтлвуд сказал: «материал о простых числах неверен» — в том смысле, что Рамануджан неправильно допускал, что дзета-функция Римана не имеет комплексных нулей, хотя на деле их бесконечно много (на эту тему у Римана была целая гипотеза). Гипотеза Римана — известная и до сих пор нерешенная математическая задача, которую оптимист-преподаватель предложил Литтлвуду в качестве проектной работы, когда тот был еще студентом.
А что насчет странного выражения Рамануджана 1 + 2 + 3 + 4 +… = -1/12? Оно также имеет отношение к дзета-функции Римана. Для положительных целых чисел ζ (s) определяется как сумма 
. В Wolfram Language есть интересная функция — Zeta[s] — которую можно получить, расширив ее область определения на все множество комплексных чисел. Затем, на основе формулы для положительных аргументов, можно сказать, что Zeta[-1] представляет собой сумму 1 + 2 + 3 + 4 +… Но можно просто вычислить Zeta[-1]:
Это слишком странный результат для того, чтобы просто в него поверить. Однако и не такой безумный, как может показаться на первый взгляд. Это результат, который в настоящее время считается вполне разумным для определенных расчетов в квантовой теории поля (в которой, если уж быть справедливым, все актуальные бесконечности предназначены для того, чтобы в конце их отменить).
Вернемся к нашей истории. У Харди и Литтлвуда не было приемлемой ментальной модели для Рамануджана. Литтлвуд предположил, что Рамануджан не хочет предоставлять доказательств, потому что он боится, что они украдут его работу (кража тогда, как и сейчас, была серьезной проблемой в научных кругах). Рамануджан сказал, что его «ранят» эти предположения, и заверил их, что он «ни в малейшей степени не опасается» за то, что его методом воспользуется кто-то еще. Он добавил, что он изобрел метод восемь лет назад, но до сих пор не нашел никого, кто смог бы оценить его, и теперь он был «готов передать… в распоряжение, все, что есть».
В то же время (еще до ответа на первое письмо Рамануджана) Харди совместно с отделом правительства, ответственного за индийских студентов, изучал, как перевести Рамануджана в Кембридж. Не вполне понятно, что произошло на этом отрезке их переписки, но Рамануджан ответил, что он не может ехать — возможно, из-за его убеждений брамина, или из-за матери, или, возможно, потому, что он просто думал, что не впишется в новую среду. Но в любом случае сторонники Рамануджана занялись тем, чтобы он получил стипендию в Университете Мадраса. Другие эксперты высказали мнение, что »его результаты замечательны;, но он не может на данный момент представить вразумительного доказательства некоторых из них»; при этом »он обладает достаточным знанием английского языка и не слишком стар, чтобы учиться современным методам из книг».
Администрация университета заявила, что их правила не позволяют дать стипендию выпускника тому, кто, как Рамануджан, не получил степень бакалавра. Однако они предложили выход: «раздел XV Закона о регистрации и статьи 3 Закона об индийских университетах от 1904 года допускает выдачу такой стипендии [со стороны Государственного Департамента Образования] при условии согласия губернатора Форт Ст. Джорджа в Совете». И, несмотря на бюрократию, дело пошло быстро, и в течение нескольких недель Рамануджан должным образом получил стипендию на два года с единственным требованием предоставлять ежеквартальные отчеты.
Стиль работы Рамануджана
К тому времени, когда он получил свою стипендию, Рамануджан стал писать больше статей и публиковать их в журнале Индийского математического общества. По сравнению с его амбициозными идеями о простых числах и расходящихся рядах тематика этих работ была совсем скучной. Тем не менее, они были замечательны.
Что сразу поражает — они полны реальных, сложных формул. Большинство математических статей не такие. Они могут быть сложно написаны и не содержать при этом больших выражений, включающих в себя сложные комбинации из корней или длинных целых чисел.
Сейчас мы привыкли видеть невероятно сложные формулы, генерируемые с помощью Mathematica. Однако они являются промежуточными шагами, а не темами для подробного обсуждения в статьях. У Рамануджана сложные формулы скрывали за собой историю. Невероятно впечатляет, что он мог вывести их без компьютеров и других современных инструментов.
(Кстати, еще в конце 1970-х годов я начал писать статьи, включавшие в себя формулы, генерируемые компьютером. И в одной конкретной статье в одной из формул много раз подряд повторялось число 9. Но опытная машинистка, которая печатала статью — да, из рукописи — заменила каждую »9» на «g». Когда я спросил ее, почему, она сказала:»Ну, в статьях никогда не бывает столько 9»!).
Другой отличительной чертой работ Рамануджана является частое использование численных приближений в качестве аргументов, приводящих к точным результатам. Люди склонны думать о работе с алгебраическими формулами как о точном процессе — например, что коэффициент в точности равен 16, а не приблизительно 15.99999. Однако для Рамануджана приближения были обычным делом, при этом окончательные результаты оказывались точными.
В каком-то смысле неудивительно, что приближения числам полезны. Скажем, мы хотим знать, что больше: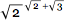 
или 
. Мы можем начать делать все виды преобразований для квадратных корней и пытаться выводить из них теоремы. Или мы можем просто оценить каждое выражение численно и обнаружить, что результат первого выражения (2,9755 …) меньше, чем второго (3,322 …). В математической традиции для кого-то вроде Харди — или, если на то пошло, в типичном современном исчислении, — такой прямой способ расчета ответа на вопрос кажется чем-то неуместным и неправильным.
И, конечно, если цифры близкие, нужно быть осторожным относительно численного округления и прочего. Хотя вот на сегодняшний день в системе Mathematica и с Wolfram Language с их встроенными системами отслеживания чисел мы часто используем численные приближения для получения точных результатов так же, как это делал Рамануджан.
Когда Харди просил у Рамануджана доказательств, отчасти он хотел лишь получить своего рода историю для каждого результата, которая объясняла бы его. Но в некотором смысле методы Рамануджана не поддаются этому способу. Легко понять, что это правда, но очень сложно доказать, почему это так.
И то же самое происходит, когда ключевая часть результата бывает получена исключительно из вычисления сложных формул, — или, в наше время, из автоматического доказательства теорем. Да, можно проследить шаги и увидеть, что они верны. Но отсутствие контекста не позволит в полной мере понять полученные результаты.
Было бы неприятно в конечном итоге получить некоторое сложное выражение или кажущееся случайным число, потому что такие результаты ни о чем не сказали бы большинству людей. Но Рамануджан отличался. Литтлвуд однажды сказал о Рамануджане, что »каждое положительное число было его личным другом». Обладая прекрасной памятью и хорошей способностью замечать закономерности, Рамануджан мог узнать многое из сложного выражения или длинного числа. Каждый объект будто сам просился рассказать ему свою историю.
Рамануджан генерировал все эти вещи своими собственными усилиями. Но в конце 1970-х и начале 1980-х гг. у меня был опыт автоматической генерации большого количества сложных результатов с помощью компьютера. Я делал это какое-то время, и случилось кое-что интересное: отныне я был в состоянии быстро распознавать «текстуру» результатов и мог сразу увидеть, что с большой степенью вероятности будет верно. Если я имел дело, скажем, с некоторыми сложным интегралом, это было не то же самое, что знать теоремы о нем. Моя интуиция работала — например, я мог предположить, какие функции появятся в результате. Учитывая это, я мог бы заставить компьютер продолжить и получить детальную картину —, а значит, и убедиться, что результат был правильным. Но при этом я не мог вывести, почему результат был истинным; я просто получал его с помощью интуиции и расчета.
Сейчас, конечно, достаточно чистой математики, где нельзя (пока что) делать вычисления для того, чтобы проверить, является или нет какой-то результат правильным. Это часто происходит, например, когда речь идет о бесконечности или бесконечно малых величинах или пределах. В 1910 году Харди написал книгу под названием Orders of Infinity — о тонкостях, которые возникают при взятии бесконечных пределов (в частности, в виде алгебраического аналога теории трансфинитных чисел; он говорил о сравнении темпов роста таких явлений, как вложенные экспоненциальные функции, и мы даже извлекли некоторую пользу из того, что теперь называют полями Харди в отношении степенных рядов в Wolfram Language).
Так что, когда Харди увидел «быстрое и свободное» обращение Рамануджана с бесконечными пределами и тому подобным, неудивительно, что он отреагировал отрицательно и подумал, что ему нужно «приручить» Рамануджана — приучить его к более тонким европейским способам получения правильных ответов.
Видеть то, что важно
Рамануджан несомненно был великим человеком-калькулятором — и особенно впечатляло его знание о том, является ли тот или иной математический факт или отношение истинными или нет. Однако самым большим его мастерством была сверхъестественная способность отличать наиболее существенное и понимать, что именно из этого можно вывести.
К примеру, возьмем его изданную в 1914 году статью «Модульные уравнения и аппроксимации числа П», в которой он проводит вычисления (без компьютера, конечно):
Большинство математиков сказали бы:»то, что результат так близок к целому числу, — лишь забавное совпадение; ну и что? » Но Рамануджан понял больше. Он нашел другие отношения (эти »=» должны быть ≅):
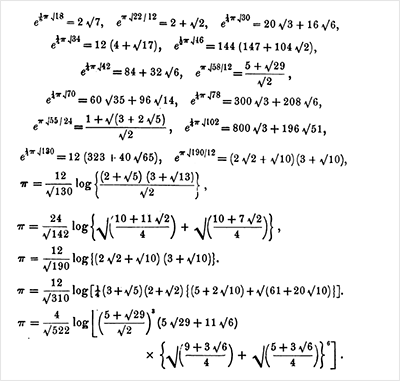
Затем он начал строить теорию, которая включает в себя эллиптические функции (хотя Рамануджан не знал еще такого названия в то время) и начал работать над новыми приближениями для пи:
Предыдущие приближения к пи были в некотором смысле гораздо более «здравыми» (хотя одним из лучших вариантов до Рамануджана была формула Мачины 1706 года), включающая в себя как будто случайное число 239:
Но странные ряды Рамануджана имели одну важную особенность: они требовали гораздо меньше условий для вычисления π с заданной точностью. В 1977 году Билл Госпер, которого я имел удовольствие знать в течение более чем 35 лет, взял последний из рядов Рамануджана из списка выше и использовал его для вычисления рекордного количества цифр числа пи. Вскоре последовали другие вычисления, основанные на идее Рамануджана — метод, который мы используем для вычисления пи в Mathematica и Wolfram Language.
Если посмотреть на статьи Рамануджана, становится понятно, что даже он сам иногда не знал, что было (или не было) статистически значимым. Например, он отметил:
И потом (это практически единственный его опубликованный пример из геометрии) он на основе этой формулы представил своеобразную геометрическую конструкцию «квадратуры круга»:
Истина или объяснение
Наверняка для Харди способ работы Рамануджана был чужд. Рамануджан был экспериментатором в математике: он свободно входил во вселенную математических возможностей и делал расчеты для того, чтобы найти интересные и значимые факты — и только затем строил теории, основанные на них.
Харди же работал в традиционном русле, постепенно расширяя описательную часть существующей математики. Большинство его работ начинаются — явно или неявно — с цитирования некоторого результата из математической литературы, а затем продолжаются рассказом о том, как этот результат может быть распространен с помощью ряда точных шагов. У него нет внезапных эмпирических открытий, как нет и необъяснимых скачков, основанных на интуиции. Его математика тщательно аргументирована и построена по кирпичику.
Столетие спустя почти все работы по математике делаются так. И даже если обсуждать один и тот же предмет, возможно, кое-что не следует называть «математикой», потому что методы слишком разные. В то время, как я собственными силами исследовал вычислительную вселенную простых программ, я сделал изрядное количество того, что можно было бы назвать «математическим» в том смысле, что, например, я исследовал системы, основанные на числах.
На протяжении многих лет я находил всевозможные интересные результаты. Причудливо вложенные рекуррентные соотношения, которые генерируют простые числа. Своеобразные представления целых чисел в виде XOR-деревьев. Но одни эмпирические факты еще не являются частью традиции существующей математики.
Для многих математиков вроде Харди процесс доказательства является основой математической деятельности. Несложно выдвинуть пред
