[Перевод] Как работает поле Хиггса: 2) почему поле Хиггса в среднем ненулевое25.08.2017 19:36

Как работает поле Хиггса:

1. Основная идея
2. Почему поле Хиггса в среднем ненулевое

Как так получается, что у поля Хиггса в природе среднее значение не равно нулю, а у других (судя по всему, элементарных) полей природы, известных нам, оно нулевое? [Очень мелкий шрифт: другие поля, за исключением гравитационного поля самого нижнего уровня, зовутся метрическими, это позволяет определить существование пространства и времени].

Во-первых, фермионные поля не могут обладать большим постоянным ненулевым значением в природе. Это связано с различием между фермионами и бозонами. Бозоны могут быть в среднем ненулевыми, но фермионы не могут. Так что можно забыть про электроны (и их кузенов мюонов и тау), про нейтрино и кварки. Мелкий шрифт: фермионы могут образовывать пары друг с другом или с антифермионами и составлять композитные бозоны, которые могут быть в среднем ненулевыми. Это так для верхних и нижних кварков и их антикварков, и для электронов в сверхпроводнике. Но это долгая история, и она не касается нашей напрямую.
Что насчёт полей фотонов, глюонов, W и Z? Всё это бозоны. В принципе у этих полей могло бы быть постоянное ненулевое среднее значение по Вселенной. Но эксперименты, а не теория, говорят, что это не так. Достаточно большая ненулевая величина электрического поля привела бы к появлению различных эффектов, которых мы не наблюдаем. Самым важным из них было бы нарушение вращательной инвариантности на крупных масштабах. Электрическое поле — это вектор (спин-1), оно указывает в определённом направлении, поэтому если оно ненулевое, то направление, в котором указывает это значение, должно отличаться от всех остальных. (Рис. 1, слева внизу).

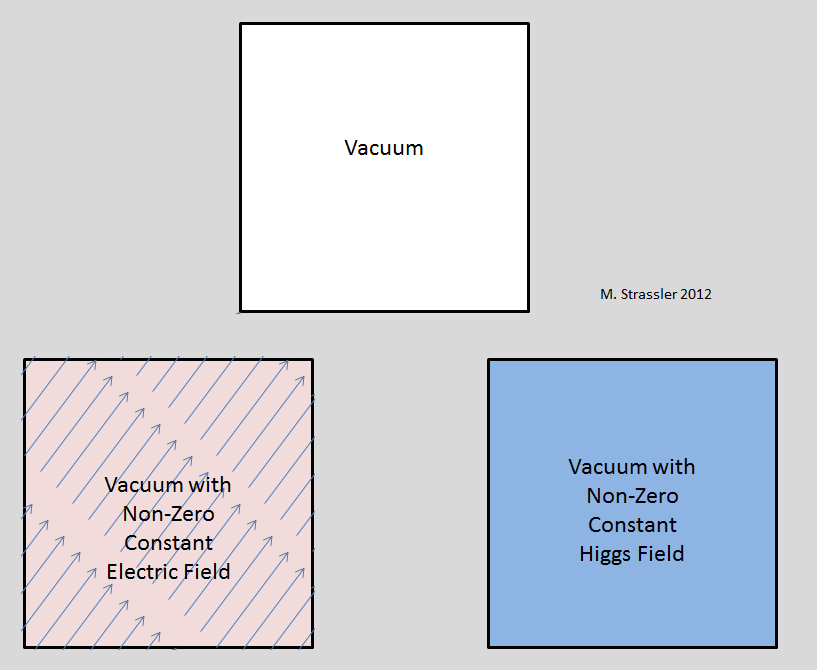
Рис. 1

Поле Хиггса же скалярное (спин-0), оно никуда не указывает. Среди других скалярных полей (не элементарные и не релятивистские) можно привести примеры поля плотности воздуха, поле давления внутри Земли, температуру океана. В каждой точке пространства и времени плотность или давление или температура — это просто число, а электрическое поле — это число и направление. Так что если у поля Хиггса ненулевое значение, никакого предпочтительного направления не возникает — рис. 1, справа внизу. Что более странно (поскольку оно релятивистское), поле Хиггса не порождает никакой предпочтительной системы отсчёта. Для плотности воздуха есть предпочтительная система отсчёта, поскольку вы либо покоитесь относительно воздуха, либо двигаетесь сквозь него. Но для поля Хиггса это не так; все наблюдатели покоятся относительно него. Поэтому успех СТО Эйнштейна, описывающей всякие явления, е противоречит присутствию релятивистского скалярного поля ненулевого значения, такого, как поле Хиггса. Вкратце, в присутствии ненулевого поля Хиггса вакуум ведёт себя точно так же, как он вёл бы себя при H = 0; его наличие можно обнаружить только через оказываемое воздействие на массы частиц (или через что-то более кардинальное, к примеру, использование БАК для создания частиц Хиггса).

Проще всего полю Хиггса было бы поддерживать ненулевое значение по всей Вселенной, если бы у него было ненулевое равновесное значение H0, участвующее в его уравнении движения класса 1:

$d^2H/dt^2 - c^2 d^2H/dx^2 = -(2 \pi \nu_{min})^2 (H - H_0)$

(Оно должно быть класса 1, а не класса 0, по причинам, которые станут нам ясны после обсуждения частицы Хиггса). На самом же деле ситуация чуть более сложная. Правильное уравнение будет выглядеть так:

$ d^2H/dt^2 - c^2 d^2H/dx^2 = a^2 H - b^2 H^3 $

Где a и b — константы (их квадраты положительные! Заметьте знак плюса перед a2H, и сравните его с минусом в предыдущем уравнении), о которых мы узнаем чуть позже. Это можно переписать как:

$ d^2H/dt^2 - c^2 d^2H/dx^2 = - b^2 H (H^2 - [a/b]^2) $

Если H (x, t) — константа в пространстве и времени, тогда dH/dt=dH/dx=0, поэтому

$ 0 = - b2 H (H2 - [a/b]^2) $

(когда H (x, t) — константа по x и t), и у него есть решения (пока мы сильно всё упростим):

1. H = 0
2. H = + a/b
3. H = — a/b

Иначе говоря, равновесных положений три, а не одно. Мелкий шрифт: я тут сильно упрощаю, но без ущерба смыслу.

Это не сразу понятно, но решение H = 0 — нестабильное. Ситуация аналогична уравнению движения шара в чаше такой формы, какая изображена на рис. 2 — похожей на дно винной бутылки. У него тоже есть три положения равновесия, одна в 0 и две в ±x0. Но очевидно положение в 0 нестабильное — любой толчок заставит красный шар далеко укатиться от х=0, кардинальное изменение ситуации. И наоборот, равновесие в х = х0 стабильное, поскольку любой толчок заставит зелёный шарик колебаться с небольшой амплитудой вокруг точки х=х0 — не такое кардинальное изменение. То же будет верным для светло-зелёного шара на х=-х0. Точно так же, хотя H = 0 будет решением уравнения для поля Хиггса, история нашей Вселенной получилась достаточно сложной для того, чтобы гарантированно как следует попинать поле Хиггса, поэтому оно никак не могло остаться в таком положении. Вместо этого поле Хиггса оказалось в решении с ненулевым значением и в стабильной ситуации.

Десятилетиями, благодаря сочетанию экспериментов и теории, нам было известно, что значение поля Хиггса (которое по традиции называют «v») равно 246 ГэВ. Это даёт нам понятие о тех константах, a и b:

a = v b = (246 GeV) b

Таким образом можно определить a через b, и можно переписать уравнение движение Хиггса:

$ d^2H/dt^2 - c^2 d^2H/dx^2 = - b^2 H (H^2 - v^2) $

Но это не даёт нам представления о самом b. В следующей статье мы узнаем о нём больше.

Теперь, хотя я всё подготовил так, что H может быть равным v или –v, не имеет значения, положительно значение поля Хиггса или отрицательно (на самом деле возможностей ещё больше, см. ниже); мир получится точно таким же, с такой же физикой, поскольку от знака H ничего не зависит. Это не становится очевидным сразу, но это так; одна подсказка — где бы вы ни нашли H в описываемых мною уравнениях или в описании того, как работает поле Хиггса, там везде появляется H2, а не просто H –, а H2 не зависит от того, H = v или H = -v. [Мелкий шрифт: на самом деле H — комплексное поле, с вещественной и мнимой частью, поэтому H может равняться v, помноженному на любое комплексное число z, у которого |z|=1; и на самом деле в уравнениях всегда появляется H*H = |H|2, а оно не зависит от z. И даже это ещё не всё! Но на сегодня пока хватит.]

Если вы найдёте способ (допустим, сталкивая друг с другом протоны на Большом адронном коллайдере) каким-то образом подтолкнуть или внести возмущение в поле Хиггса, оно будет колебаться туда и сюда — то есть, в нём появятся волны в виде

$H = v + A cos[2 \pi (\nu t – x / \lambda)]$

Где А — амплитуда волны, ν и λ — частота и длина волны, а взаимоотношение между ν и λ зависит от точной формы уравнения движения, в частности, от b и v. Поскольку поле Хиггса — квантовое, у этих волн будет квантоваться амплитуда, и квант этих волн мы и называем частицей Хиггса. В следующий раз мы рассмотрим свойства этих частиц.