[Перевод] Как мы чуть не взломали шифровальщик Phobos с помощью CUDA27.02.2023 06:16

Последние два года мы работали над доказательством концепции дешифратора для программ-вымогателей семейства Phobos. По причинам, которые мы объясним здесь, он непрактичен. До сих пор у нас не получилось использовать его, чтобы помочь реальной жертве. Но мы решили опубликовать результаты и инструменты в надежде, что кто-то найдёт их полезными, интересными или продолжит исследования.

Опишем уязвимость и то, как мы понизили вычислительную сложность и повысили производительность дешифратора, чтобы достичь почти практической реализации. Продолжение — к старту нашего курса «Белый хакер»

Что, где, когда

Фобос — внутренний и самый крупный естественный спутник Марса. А ещё это название распространённого семейства программ-вымогателей — Phobos, впервые замеченного в начале 2019 года. Программа не очень интересная — она имеет много общего с «Дхармой» и, вероятно, написана теми же авторами.

Мы начали исследование после того, как за короткое время шифровальщиком Phobos были зашифрованы несколько важных польских организаций. Стало ясно, что необычна функция расписания ключей Phobos; можно даже сказать, что она сломана. Это побудило провести дальнейшие исследования в надежде создать дешифратор.

Реверс-инжиниринг

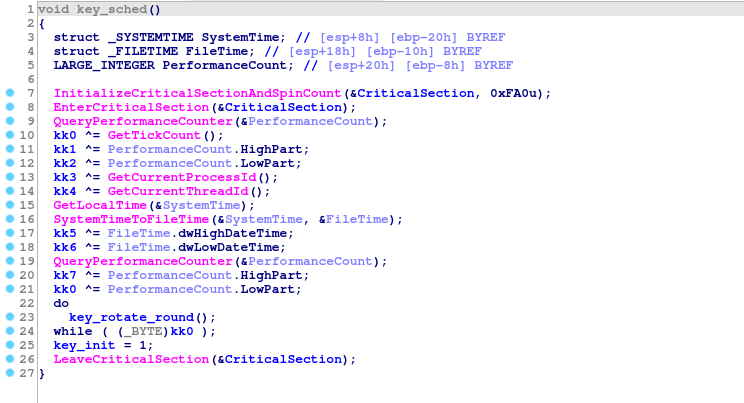
Пропустим скучные детали: функции защиты от отладки, удаление теневых копий, функция обхода основного диска и т. д. Самая интересная функция для нас — это расписание ключей:

Любопытно, что вместо одного хорошего источника энтропии автор вредоноса решил использовать несколько плохих. В списке есть:

• Два вызова функции QueryPerformanceCounter ().
• GetLocalTime () + SystemTimeToFileTime ().
• GetTickCount ().
• GetCurrentProcessId ().
• GetCurrentThreadId ().

Наконец, применяется переменное, но детерминированное число раундов SHA-256. В среднем для проверки ключа требуется 256 исполнений SHA-256 и одно дешифрование AES.

Это сразу зазвучало в наших головах тревожными колоколами. Предполагая, что время заражения известно с точностью до 1 секунды (например, через временные метки файлов или логи), получается, что количество операций, необходимых для перебора каждого компонента, равно:

Операция Количество операций

QueryPerformanceCounter 1 10**7

QueryPerformanceCounter 2 10**7

GetTickCount 10**3

SystemTimeToFileTime 10**5

GetCurrentProcessId 2**30

GetCurrentThreadId 2**30

Очевидно, что каждый компонент можно брутфорсить независимо, ведь 10**7 для современных компьютеров не так уж много. Но можно ли восстановить весь ключ целиком?

Сколько ключей нам на самом деле нужно проверить?

Начальное состояние (141 бит энтропии)

Количество ключей для наивной атаки методом перебора равно:

>>> 10**7 * 10**7 * 10**3 * 10**5 * 2**30 * 2**30 * 256
2951479051793528258560000000000000000000000
>>> log(10**7 * 10**7 * 10**3 * 10**5 * 2**30 * 2**30 * 256, 2)
141.08241808752197  # that's a 141-bit number

Огромное, непостижимо большое число. Ни малейшего шанса на брутфорс.

Но мы не из тех, кто легко сдаётся.

Могу я получить ваш PID? (81 бит энтропии)

Начнём с некоторых предположений. Одно мы уже сделали: благодаря системным/файловым журналам мы знаем время с точностью до 1 секунды. Одним из источников таких данных могут быть журналы событий Windows:

События по умолчанию, которое срабатывает для каждого нового процесса, нет, но при достаточном внимании к анализу часто удается восстановить PID и TID процесса-вымогателя.

Даже если установить их невозможно, поскольку PID Windows последовательны, почти всегда можно ограничить их на значительную величину. Таким образом, обычно нам не придётся перебирать всё пространство в 2**30.

Предположим, что мы уже знаем PID и TID (основного потока) процесса программы-вымогателя. Не волнуйтесь, это самое большое допущение во всей этой статье. Облегчит ли это наше положение?

>>> log(10**7 * 10**7 * 10**3 * 10**5 * 256, 2)
81.08241808752197

81 бит энтропии — слишком много, чтобы думать о брутфорсе, но кое-чего мы добились.

Δt = t1 — t0 (67 бит энтропии)

Вот другое разумное предположение: два последовательных вызова QueryPerformanceCounter вернут аналогичные результаты. В частности, второй QueryPerformanceCounter всегда будет немного больше первого. Выполнять полный перебор обоих счётчиков нет необходимости — мы можем перебрать первый, а затем предположить время между исполнениями.

Если взять код как пример, вместо

for qpc1 in range(10**7):
    for qpc2 in range(10**7):
        check(qpc1, qpc2)

можно написать:

for qpc1 in range(10**7):
    for qpc_delta in range(10**3):
        check(qpc1, qpc1 + qpc_delta)

Число 10**3 определено как достаточное эмпирически. В большинстве случаев этого должно быть достаточно, хотя это всего лишь 1 мс, поэтому в случае очень неудачного переключения контекста произойдёт сбой. Всё же попробуем:

>>> log(10**7 * 10**3 * 10**3 * 10**5 * 256, 2)
67.79470570797253

В любом случае кому нужно точное время? (61 бит энтропии)

2**67 вызовов sha256 — много, но число становится управляемым: по стечению обстоятельств оно почти точно соответствует текущему хешрейту BTC. Если вместо бессмысленного сжигания электричества всю сеть BTC перепрофилировать на расшифровку жертв Phobos, то эта сеть расшифровывала бы одну жертву за секунду, предполагая, что PID и TID известны.

Итак, SystemTimeToFileTime может обладать точностью в 10 мс. Но GetLocalTime — нет:

Это означает, что нужно перебрать только 10**3 вариантов, а не 10**5:

>>> log(10**7 * 10**3 * 10**3 * 10**3 * 256, 2)
61.150849518197795

Математическое время (51 бит энтропии)

Может быть, получится найти алгоритм лучше? Более очевидных вещей для оптимизации нет.

Обратите внимание, что key[0] равен GetTickCount () \^ QueryPerformanceCounter ().Low. Наивный алгоритм перебора проверит все возможные значения обоих компонентов, но в большинстве случаев добиться можно гораздо большего. Например, 4 ^ 0 == 5 ^ 1 == 6 ^ 2 = ... == 4. Нас волнует только конечный результат, поэтому значения таймера, которые в итоге являются одним и тем же ключом, можно игнорировать.

Простой способ сделать это выглядит так:

def ranges(fst, snd):
    s0, s1 = fst
    e0, e1 = snd
    out = set()
    for i in range(s0, s1 + 1):
        for j in range(e0, e1 + 1):
            out.add(i ^ j)
    return out

К сожалению, такое требует довольно больших затрат процессора (мы хотим выжать как можно больше производительности). Оказывается, есть рекурсивный алгоритм лучше. Он позволяет не тратить время на дубликаты, но довольно тонкий и не очень элегантный:

uint64_t fillr(uint64_t x) {
    uint64_t r = x;
    while (x) {
        r = x - 1;
        x &= r;
    }
    return r;
}

uint64_t sigma(uint64_t a, uint64_t b) {
    return a | b | fillr(a & b);
}

void merge_xors(
    uint64_t s0, uint64_t e0, uint64_t s1, uint64_t e1,
    int64_t bit, uint64_t prefix, std::vector *out
) {
    if (bit < 0) {
        out->push_back(prefix);
        return;
    }

    uint64_t mask = 1ULL << bit;
    uint64_t o = mask - 1ULL;

    bool t0 = (s0 & mask) != (e0 & mask);
    bool t1 = (s1 & mask) != (e1 & mask);

    bool b0 = (s0 & mask) ? 1 : 0;
    bool b1 = (s1 & mask) ? 1 : 0;

    s0 &= o;
    e0 &= o;
    s1 &= o;
    e1 &= o;

    if (t0) {
        if (t1) {
            uint64_t mx_ac = sigma(s0 ^ o, s1 ^ o);
            uint64_t mx_bd = sigma(e0, e1);
            uint64_t mx_da = sigma(e1, s0 ^ o);
            uint64_t mx_bc = sigma(e0, s1 ^ o);

            for (uint64_t i = 0; i < std::max(mx_ac, mx_bd) + 1; i++) {
                out->push_back((prefix << (bit+1)) + i);
            }

            for (uint64_t i = (1UL << bit) + std::min(mx_da^o, mx_bc^o); i < (2UL << bit); i++) {
                out->push_back((prefix << (bit+1)) + i);
            }
        } else {
            merge_xors(s0, mask - 1, s1, e1, bit-1, (prefix << 1) ^ b1, out);
            merge_xors(0, e0, s1, e1, bit-1, (prefix << 1) ^ b1 ^ 1, out);
        }
    } else {
        if (t1) {
            merge_xors(s0, e0, s1, mask - 1, bit-1, (prefix << 1) ^ b0, out);
            merge_xors(s0, e0, 0, e1, bit-1, (prefix << 1) ^ b0 ^ 1, out);
        } else {
            merge_xors(s0, e0, s1, e1, bit-1, (prefix << 1) ^ b0 ^ b1, out);
        }
    }
}

Возможно, есть алгоритм проще или быстрее, но авторы при работе над дешифратором о нём не знали.

Вот энтропия после этого изменения:

>>> log(10**7 * 10**3 * 10**3 * 256, 2)
51.18506523353571

Это было последнее снижение сложности. Чего здесь не хватает, так это хорошей реализации.

Скорость

Наивная реализация на Python (500 ключей в секунду)

Оригинальное PoC на Python тестировало 500 ключей в секунду. Для перебора 10**11 ключей ему требуется 2314 процессорных дней. Это далеко не практично. Но Python, по сути, самый медленный с точки зрения высокопроизводительных вычислений. Можно добиться большего.

Обычно в подобных ситуациях мы бы реализовали собственный дешифратор (на C++ или Rust). Но здесь даже этого недостаточно.

Время творит чудеса

Мы решили добиться максимальной производительности и внедрить наш решатель в CUDA.

Первые шаги CUDA (19166 ключей в минуту)

Наша первая наивная версия смогла взломать 19166 ключей в минуту. У нас не было опыта работы с CUDA, мы допустили много ошибок; статистика использования графического процессора выглядела так:

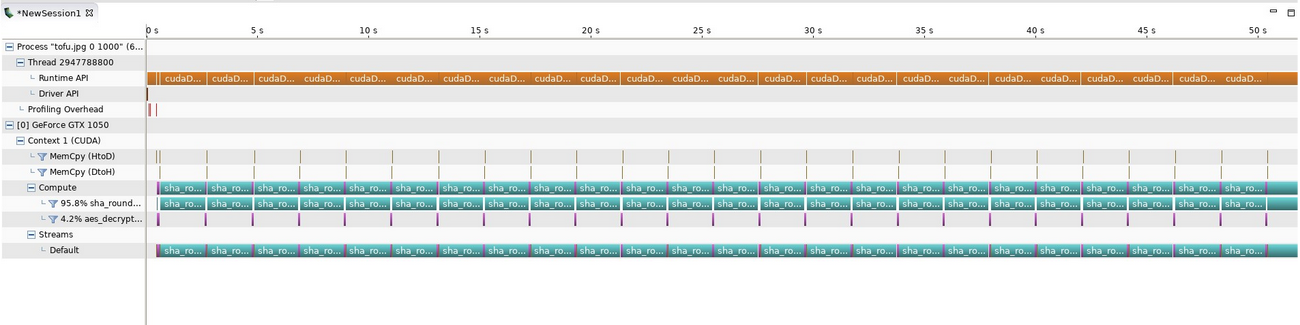
Улучшение sha256 (50000 ключей в минуту)

Очевидно, огромным узким местом оказался sha256: вызовов sha256 в 256 раз больше, чем AES. Большая часть работы здесь сосредоточена на упрощении и адаптации кода.

Например, мы встроили sha256_update:

Встроили sha256_init:

Заменили глобальные массивы локальными переменными:

Жёстко задали размер данных в 32 байта:

И сделали несколько операций более подходящими для графического процессора, например, для bswap использовали __byte_perm.

В конце концов, изменился основной цикл:

После этой оптимизации мы поняли, что код теперь делает много ненужных копий и переносов данных. Сейчас копии не нужны:

Всё это позволило нам повысить производительность в 2,5 раза — до 50 тыс. ключей в минуту.

Распараллелим алгоритм (105000 ключей в минуту)

Работа разделена на потоки, и потоки выполняют логические операции. В частности, memcopy на графическую карту и с неё может выполняться одновременно с нашим кодом без потери производительности.

Просто изменив наш код для более эффективного использования потоков, мы смогли удвоить производительность до 105 тыс. ключей в минуту:

И, наконец, AES (818000 ключей в минуту)

Несмотря на все эти изменения, мы даже не пытались оптимизировать AES. После всех полученных уроков это было довольно просто. Мы просто искали шаблоны, которые плохо работали на GPU, и делали код лучше. Например:

Мы изменили наивный цикл for на развёрнутую вручную версию, которая работала с 32-битными целыми.

Это может показаться мелочью, но на самом деле пропускная способность стала значительно выше:

…а теперь параллельно (100 млрд. ключей в минуту)

В запасе у нас был последний трюк — запускать один и тот же код на нескольких GPU! Удобно, что у нас есть небольшой кластер GPU на CERT.PL. Мы выделили две машины с общим количеством графических процессоров Nvidia в 12. Пропускная способность сразу увеличилась почти до 10 миллионов ключей в минуту.

Таким образом, перебор 10**11 ключей в кластере занимает всего 10 187 секунд (2,82 часа). Звучит заманчиво, правда?

Где всё пошло не так?

К сожалению, как мы упоминали в начале, существует множество практических проблем, которые мы кратко рассмотрели, это даже усложнило публикацию дешифратора:

• Требуется знание TID- и PID-параметров. Это затрудняет автоматизацию дешифратора.
• Мы предполагаем очень точные измерения времени. К сожалению, такое измерение осложняют дрейф часов и шум, преднамеренно вносимый в счётчики производительности Windows.
• Уязвима не каждая версия Phobos. Перед развёртыванием дорогостоящего дешифратора требуется реверс-инжиниринг для подтверждения семейства.
• Даже после всех улучшений код слишком медленный для запуска на компьютере потребительского класса.
• Жертвы не хотят ждать исследователей без гарантии успеха.

Вот почему мы решили опубликовать эту статью и исходный код (почти работающего) дешифратора. Надеемся, что это позволит исследователям вредоносных программ по-новому взглянуть на тему и, возможно, даже расшифровывать жертв программ-вымогателей.

Мы опубликовали исходный код CUDA. Он содержит краткую инструкцию, пример конфигурации и набор данных для проверки программы.

Проанализированный образец программы-вымогателя: 2704e269fb5cf9a02070a0ea07d82dc9d87f2cb95e60cb71d6c6d38b01869f66 | MWDB | VT

Полезная теория и интересная практика — на наших курсах:

© Habrahabr.ru