[Перевод] История Шипастика

Шипастики повсюду
Мы зовём его «Шипастиком» [Spikey], и в своей сегодняшней жизни я встречаюсь с ним постоянно:

Он происходит от трёхмерного объекта, многогранника под названием «ромбический шестидесятигранник».
Но какова его история и почему мы сделали его своим символом?
Происхождение Шипастика
В 1987 году, когда мы разрабатывали первую версию Mathematica, одной из её инноваций стала возможность генерации не зависящей от разрешения трёхмерной графики на основе символьных описаний. В ранних демонстрациях это позволило нам выдавать удивительно чёткие изображения правильных многогранников. Но, приближаясь к релизу Mathematica 1.0, мы захотели использовать какой-то более впечатляющий пример. Поэтому мы решили взять последний правильный многогранник — икосаэдр — и сделать из него что-то более сложное путём придания ему звёздчатой формы, или, что более корректно, кумуляции. Да, именно так выглядел первый интерфейс записной книжки, 30 лет тому назад.

Сначала это была просто симпатичная демонстрация, которая довольно быстро работала на тогдашних наших компьютерах. Но вскоре трёхмерный объект, генерируемый ею, стал де-факто использоваться в качестве логотипа для Mathematica. И к моменту выхода версии 1.0 в 1988 году звёздчатый икосаэдр был повсюду:

Со временем стали появляться различные посвящения нашему звёздчатому многограннику — выполненные в разных материалах и размерах:

Но, спустя всего год после выхода Mathematica 1.0, мы были готовы выпустить Mathematica 1.2, и чтобы передать усложнение продукта, нам требовался усложнённый логотип. Один из наших разработчиков, Игорь Ривин, защитил докторскую на тему многогранников в гиперболическом пространстве — и благодаря его усилиям наши материалы для версии 1.2 украсил гиперболический икосаэдр:

Мои сотрудники подарили на мой 30-й день рождения в 1989 году футболку с современным тогда Шипастиком, и цитатой, которую я поддерживаю и спустя столько лет:

«Компания — это весело»
После выхода Mathematica 1.2 в наших маркетинговых материалах можно было встретить целую коллекцию гиперболических правильных многогранников, но с появлением в 1991 версии 2.0 мы решили, что больше всего нам нравился гиперболический икосаэдр:

Но мы продолжали исследовать и другие шипастые формы. Вдохновившись рисунком Леонардо да Винчи «деревянной модели» звёздчатого икосаэдра (выполненным с удивительно точным соблюдением перспективы) для книги Луки Пачоли «О божественной пропорции», мы заказали плакат версии 2.0, где пять пересекающихся тетраэдров расположены так, что их внешние вершины образуют додекаэдр:

Сегодня, просматривая мои архивы от 1991 года, я нахожу «поясняющий» код, и приятно видеть, что он запросто выполняется в нашей последней версии Wolfram Language (хотя сегодня его можно записать чуть элегантнее):

С годами это стало странным ритуалом — готовясь к запуску следующей основной версии Mathematica, мы организуем серьёзные встречи, где занимаемся «выбором нового Шипастика». Иногда выбирать приходится из сотен разных вариантов, созданных с использованием совершенно разных алгоритмов:

Но, хотя цветовые палитры видоизменяются, и Шипастики часто отражают наличие новых возможностей в системе (пусть и несколько подспудно), у нас есть 30-летняя традиция выбора вариантов гиперболического додекаэдра:

В последнее стало принято изучать параметрическое пространство — хотя сейчас мы накопили уже сотни параметров:
https://blog.stephenwolfram.com/data/uploads/2018/12/spikey-maker-notebook-video.mp4
У гиперболического додекаэдра 20 вершин — это идеально подходило для празднования 20-летия Mathematica в 2008-м. Но когда мы захотели сделать что-то подобное на 25-летие в 2013-м, мы столкнулись с проблемой отсутствия правильных многогранников с 25-ю вершинами. Но (по сути, используя функцию SpherePoints[25]), мы смогли создать приблизительную фигуру, и распечатали её на 3D-принтере для всех сотрудников компании, с размерами, соответствующими стажу сотрудников.

Выход Wolfram|Alpha
В 2009 мы готовились к выходу Wolfram|Alpha, и системе требовался логотип. Концепций было множество:

Нам хотелось подчеркнуть, что Wolfram|Alpha работает при помощи вычислений, а не, допустим, как поисковик. И какое-то время мы хотели использовать что-то с шестерёнками. Но нам также хотелось, чтобы логотип напоминал давнишний логотип Mathematica. Это породило один из тех проектов типа «наш генеральный сошёл с ума»: создание шестерёнчатого механизма из шипастых форм.
Давний пользователь Mathematica и Wolfram Language, инженер-механик из Венгрии Сандор Кабай помог нам, предложив «шипастые шестерни»:
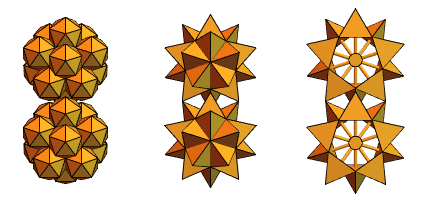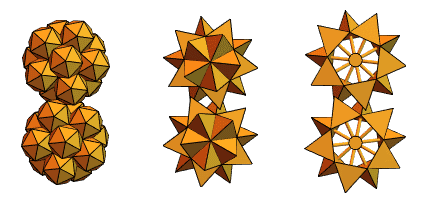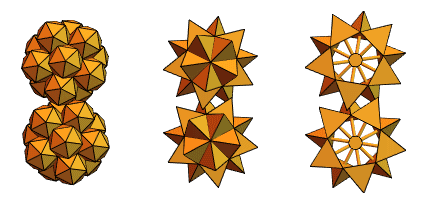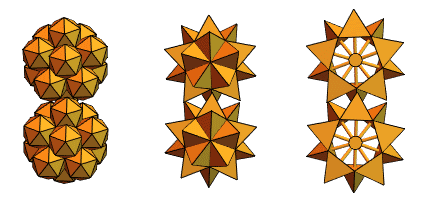
Вернувшись к пересекающимся тетраэдрам из 2-й версии, он сотворил нечто такое:

В 2009-м году стали очень популярными 3D-принтеры, и мы думали, что будет неплохо сделать для Wolfram|Alpha логотип, который можно будет распечатать. Гиперболический многогранник не подходил — шипы могли отломаться и представлять угрозу. У фигур вроде шипастика 4-й версии, с «безопасными шипами», недоставало элегантности.
Какое-то время мы цеплялись за идею с шестерёнками. Но в итоге решили, что стоит ещё раз взглянуть на обычные многогранники. Но какой многогранник мы можем себе выбрать?
Конечно, возможных многогранников существует бесконечное количество. Но для нашего логотипа мы хотели выбрать симметричный и до какой-то степени «правильный» многогранник. Пять правильных многогранников (или «Платоновых тел») — грани которых представляют собой одинаковые правильные многоугольники — можно считать «самыми правильными» из всех:

Существует ещё 13 архимедовых тел — у них идентичные вершины, а в качестве граней выступают правильные многоугольники, хотя и разных типов:
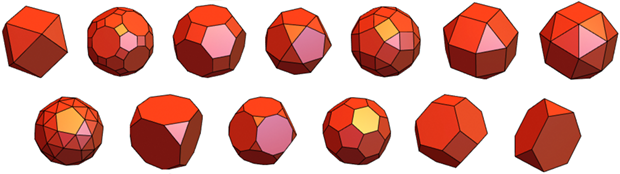
Типов «правильности» многогранников можно придумать множество. Один из примеров — «однородные многогранники», которые демонстрирует плакат из журнала The Mathematica Journal от 1993:

За те годы, что Эрик Вайштайн собирал коллекцию, которая к 1999 году превратилась в MathWorld, он попытался включить в неё статьи по как можно большему количеству чем-либо примечательных многоугольников. В 2006, в рамках включения в Mathematica и Wolfram Language различных систематизированных данных, мы стали включать в них и данные по многоугольникам с MathWorld. В результате после выпуска версии 6.0 в 2007-м в ней появилась функция PolyhedronData, где содержались исчерпывающие данные по 187 примечательным многоугольникам:

В Mathematica и Wolfram Language всегда можно было генерировать правильные многоугольники, но теперь это стало делать проще. С версией 6.0 мы выпустили также и Wolfram Demonstrations Project, который быстро стал пополняться различными демонстрациями, связанными с многогранниками.
Одна из них была сделана моей дочерью Катериной, когда ей было 10 лет (сегодня она продолжает развиваться в направлениях, связанных с геометрией): это «многогранные коалы», с разбивкой по всем используемым многогранникам из PolyhedronData[]:

Вот на таком фоне в 2009-м мы захотели «выбрать многогранник» для Wolfram|Alpha. Решилось всё в пятницу 6 февраля, когда я взялся за дело сам.
У меня сохранилась та записная книжка, и по ней видно, что сначала я пытался реализовать сомнительную идею размещения сфер в вершинах многогранников:

Но, как записано в истории Notebook History, всего две минуты спустя я уже перешёл к чистым многогранникам — все они были оранжевого цвета, который мы тогда хотели использовать для логотипа:
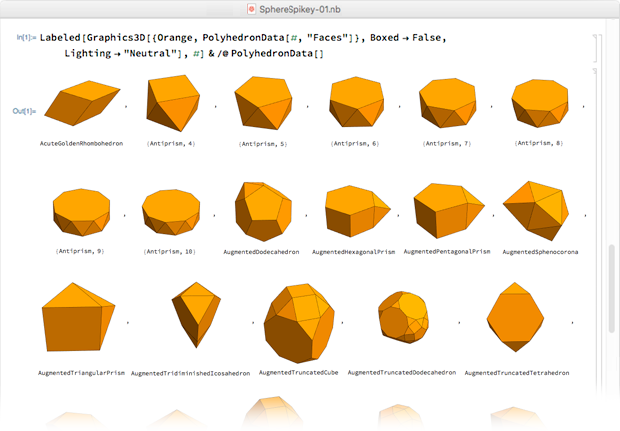
Многогранники выстраивались в алфавитном порядке по названиям, и на 28-й строке появился он — ромбический шестидесятигранник.

Пару минут спустя, в 00:24:24, 7 февраля 2009 года, я обнаружил этот ромбический шестидесятигранник и развернул его в симметричное положение, которое мы и используем ныне:

Мне захотелось посмотреть, как он будет выглядеть в серых цветах и в виде силуэта, и четыре минуты спустя я использовал ColorSeparate, чтобы выяснить это:
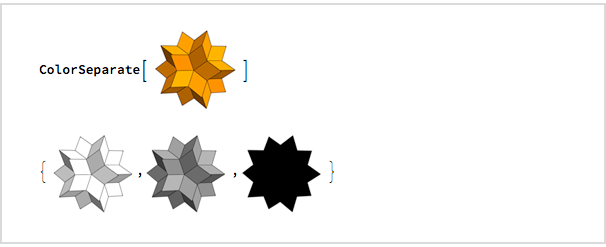
Я сразу начал писать e-mail, который я отправил в 00:32:
Мне очень нравится RhombicHexecontahedron. У него интересная и очень симметричная форма. Мне кажется, его точность как раз подходит нам, а силуэт выглядит довольно разумно.

Я, очевидно, просто скопировал RhombicHexecontahedron из записной книги (сомневаюсь, что смог бы без ошибок написать «шестидесятигранник» [hexecontahedron]). Из моих архивов мне известно, что это был первый раз, когда я написал название многогранника, которому суждено будет стать моим самым любимым.
В Wolfram Language было очень просто получить изображение ромбического шестидесятигранника, и поиграться с ним:
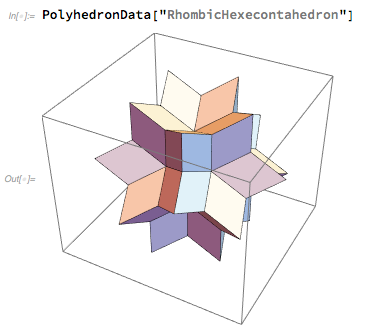
К понедельнику было ясно, что победил ромбический шестидесятигранник — и наш изобразительный департамент занялся его отрисовкой в качестве логотипа для Wolfram|Alpha. Мы пробовали различные его ориентации, но в итоге остановились на симметричном положении «в анфас», выбранном мною. (Также нам нужно было выбрать наилучшее «фокусное расстояние» для наиболее подходящего ракурса).

Как и у нашего звёздчатого икосаэдра от версии 1.0, у ромбического шестидесятигранника 60 граней. Но каким-то образом, благодаря «пятилепестковым» комбинациям, он выглядит гораздо более элегантным. Довольно много усилий было потрачено на то, чтобы подобрать такое затенение граней, чтобы двумерный рисунок правильно отражал трёхмерный объект. Но вскоре мы представили первую официальную версию своего логотипа:

Она быстро стала появляться повсеместно, и, как дань нашим ранним идеям, часто на фоне, украшенном шестерёнками:

Несколько лет спустя мы немного подправили затенение граней, что и привело к созданию логотипа Wolfram|Alpha, использующегося до сих пор:

Ромбический шестидесятигранник
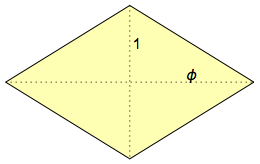
Что же такое ромбический шестидесятигранник? По-английский он называется hexecontahedron, поскольку у него 60 граней, а ἑξηκοντα (хексеконта) — это греческое слово, обозначающее »60». Его грани — это золотые ромбы, которые называются так потому, что их диагонали соотносятся друг с другом соответственно золотому сечению: φ = (1 + √5)/2 ≃ 1,618:
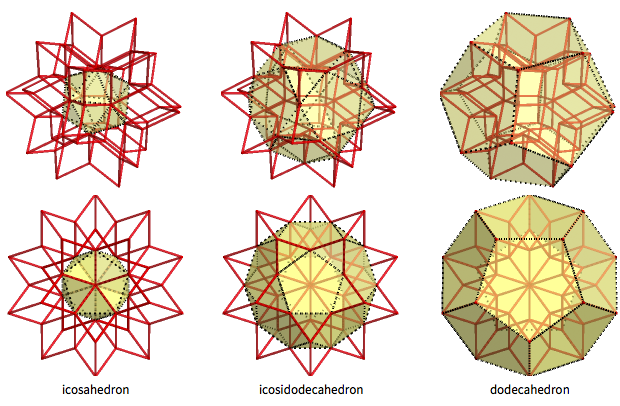
Ромбический шестидесятигранник — интересное промежуточное тело между икосаэдром и додекаэдром (с икосододекаэдром между ними). 12 внутренних вершин ромбического шестидесятигранника формируют правильный икосаэдр, а 20 внешних вершин — правильный додекаэдр. 30 «промежуточных вершин» формируют икосододекаэдр, 32-гранник (у него 20 треугольных и 12 пятиугольных граней):
В сумме, у ромбического шестидесятигранника 62 вершины и 120 рёбер (а также 120–62+2 = 60 граней). У него три типа вершин («внутренние», «средние» и «внешние»), соответствующие 12+30+20 вершинам икосаэдра, икосододекаэдра и додекаэдра. У этих вершин сходятся вместе соответственно по 3, 4 и 5 рёбер. У каждой грани есть одна «внутренняя» вершина, в которой сходятся 5 рёбер, одна внешняя вершина, где сходятся три ребра, и две «промежуточные», где сходятся 4 ребра. Внешняя и внутренняя вершины — остроугольные вершины золотых ромбов, а промежуточные — тупоугольные.
Угол у остроконечных вершин золотых ромбов равен 2 tan−1 (φ−1) ≈ 63,43°, а у тупоконечных — 2 tan−1 (φ) ≈ 116,57°. Такие углы позволяют собрать ромбический шестидесятигранник из конструктора Zometool, используя только красные опоры (как и в случае с додекаэдром):

Из 120 рёбер ромбического шестидесятигранника у 60 «внутренних шарниров» двугранный угол равен 4π/5=144°, а у 60 внешних он равен 2π/5=72°. Углы, стягиваемые внешними и внутренними вершинами, равны π/5 и 3π/5.
Чтобы нарисовать ромбический шестидесятигранник, необходимо знать трёхмерные координаты его вершин. Их удобно получить, используя тот факт, что ромбический шестидесятигранник инвариантен относительно группы икосаэдра, поэтому можно начать с одного золотого ромба и просто добавить 60 матриц, формирующих трёхмерное представление группы икосаэдра. Это, к примеру, даёт итоговые координаты вершин в {±φ, ±1,0}, {±1, ±φ, ±(1+φ)}, {±2φ,0,0}, {±φ, ±(1+2φ),0}, {±(1+φ), ±(1+φ), ±(1+φ)} и их циклические перестановки со всеми возможными знаками.
Кроме того, что грани ромбического шестидесятигранника — это золотые ромбы, ромбический шестидесятигранник можно сконструировать из 20 золотых ромбоэдров (у которых все шесть граней — золотые ромбы):

Есть и другие способы создания ромбический шестидесятигранник из других многогранников. Его можно получить из пяти пересекающихся кубов и из 182 додекаэдров, соприкасающихся гранями:

Из ромбических шестидесятигранников нельзя выложить непрерывную мозаику, но они хорошо зацепляются друг с другом (и, да, я видел, как десятки бумажных Шипастиков складывались таким способом):

Также из них можно сделать всякие кольца и другие конфигурации:
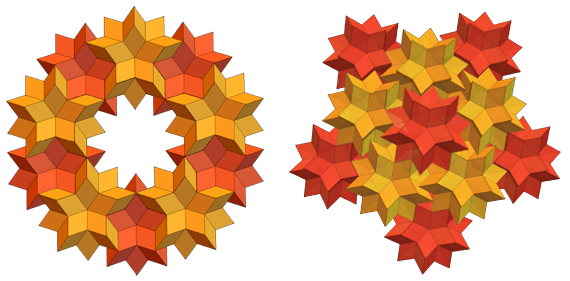
Близким родственником ромбического шестидесятигранника (РШ) является ромбический тридцатигранник (РТ). У РШ и РТ есть грани, представляющие собой золотые ромбы. Но у РШ их 60, а у РТ их 30. Вот, как выглядит отдельный РТ:

Несколько РТ прекрасно вкладываются в «кармашки» РШ, и получаются подобные вещи:

Упомянутый ранее Сандор Кабай заинтересовался РШ и РТ около 2002 года. И после запуска Wolfram Demonstrations Project он вместе со словенским математиком Исидором Хафнером добавили к проекту более сотни демонстраций, связанных с РШ, РТ и множеством их свойств:

Бумажные модели Шипастика
Как только мы определились, что Шипастик будет РШ, мы начали делать его 3D-модели. Сейчас это очень просто сделать при помощи функции Printout3D[PolyhedronData[…]], а на сторонних ресурсах можно найти уже просчитанные модели.
В мае 2009 при запуске Wolfram|Alpha у нас было под рукой уже множество трёхмерных Шипастиков:

Но, готовясь к первому праздничному сезону после этого события, мы решили дать каждому возможность сделать своего трёхмерного Шипастика. Сначала мы рассматривали вариант с 20-ю ромбоэдрическими магнитами, покрытыми пластиком. Но они выходили дорогими, и не очень хорошо слипались вместе.
Это привело нас к идее изготовления Шипастика из бумаги или тонкого картона. Поэтому сначала мы захотели сделать схему, которую можно было сложить в Шипастика:

Тестировщиком служила моя дочь Катерина (и тестовый образец до сих пор у неё), но стало ясно, что в процессе складывания проявляется очень много неудобных ситуаций, в которых неясно, как перейти из одного положения в другое. Раскладок можно сделать огромное количество (только для додекаэдра и икосаэдра их существует 43 380) — и мы подумали, что, возможно, из них получится выбрать что-то получше:
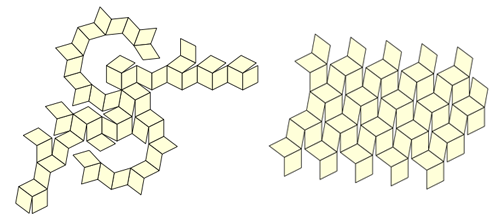
Но, когда нам не удалось найти такую схему, у нас появилась новая (пусть и очевидная) идея: если моделька будет держаться за счёт ушек, почему бы не сделать её из нескольких кусочков? Мы быстро поняли, что для этого нужно взять всего 12 идентичных кусочков такого вида:

С их помощью мы и создали наши «наборы для бумажных скульптур»:

Интересной задачей стало написание лёгкой для понимания инструкции, но после нескольких итераций инструкции стали хорошо отработанными и простыми:
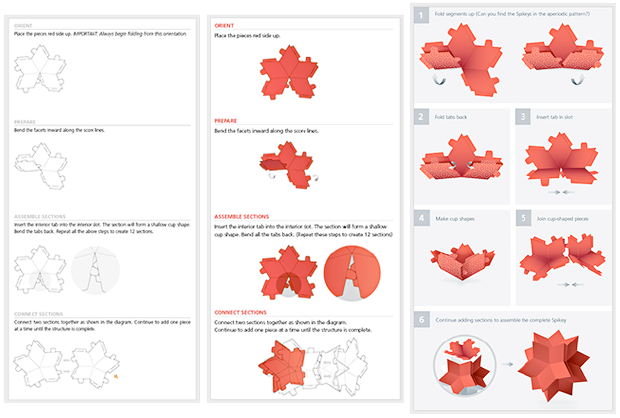
И после того, как бумажные Шипастики пошли в народ, наши пользователи начали присылать нам всяческие изображения Шипастиков «на местах»:

Путь к ромбическому шестидесятиграннику

Многогранный кубик из древнего Египта
Неизвестно, кто первым описал платоновы тела. Возможно, это сделали пифагорейцы (жившие недалеко от таких больших залежей многогранных кристаллов пирита). Возможно, это сделал кто-то задолго до них. Возможно, это был современник Платона, Теэтет Афинский. Но, в любом случае, ко времени Платона (ок. 400 г. до н.э.), было известно пять платоновых тел. А когда Евклид писал свои «Элементы» (ок. 300 г до н.э.), одним из столпов этого труда было доказательство отсутствия других правильных многогранников. Это доказательство известно тем, что делает наибольшее количество шагов от изначальных аксиом Евклида — 32.
Платоновы тела использовали для игральных костей и орнаментов. Но ещё им была отведена центральная роль в размышлениях о природе — к примеру, Платон предполагал, что в некотором смысле из них может состоять всё: земля из кубов, воздух из октаэдров, вода из икосаэдров, огонь из тетраэдров, а небеса («эфир») из додекаэдров.
А что насчёт других многогранников? В IV веке н.э. Папп Александрийский писал, что за пару столетий до этого Архимед открыл 13 других «правильных многогранников» — видимо, то, что сейчас называется архимедовыми телами — хотя подробности этого утеряны. И в течение тысячи лет с многогранниками мало что происходило. Но в XV веке с началом эпохи Возрождения многогранники внезапно снова вошли в моду. Леонардо да Винчи и Альбрехт Дюрер регулярно использовали их в искусстве и дизайне, заново открывая некоторые из архимедовых тел –, а также обнаруживая новые многогранники, например, икосододекаэдр.
Но самым крупным шагом вперёд для многогранников стала работа Иоганна Кеплера в начале XVII века. Всё началось с элегантной, пусть и совершенно неверной теории. Кеплер, исходя из теологических предпосылок, считал, что Вселенная должна быть создана с математической точностью, и предположил, что шесть планет, известных в то время, двигаются по вложенным сферам, вписанным и описанным вокруг пяти платоновых тел:

В своей книге 1619 года Harmonices mundi, «Гармония мира», Кеплер доказывал, что многие особенности музыки, планет и душ работают согласно схожим геометрическим соотношениям и принципам. Для подтверждения аргументов Кеплер изучал многоугольники и многогранники, особенно интересуясь объектами, составляющими полные наборы, вроде платоновых тел.
Он изучал «контактные многогранники», которыми можно вымостить плоскость — и нашёл, к примеру, «чудовищные плитки», как он их называл (состоящие из пятиугольников, пентаграмм и десятиугольников). Он изучал «звёздчатые многогранники» и нашёл различные звёздчатые варианты платоновых тел (и тело Кеплера — Пуансо). В 1611 он опубликовал небольшую книгу касаемо шестигранной структуры снежинок, написанную в качестве подарка на новый год одному из его покровителей. В этой книге он обсуждал трёхмерную упаковку сфер (и сферических атомов), предложив гипотезу о том, что плотнейшей упаковкой шаров в трёхмерном пространстве (мы регулярно наблюдаем её реализацию в упаковках фруктов в магазинах) является гранецентрированная кубическая упаковка (эту гипотезу формально доказали только после 2000 года — с помощью Mathematica).
В различных упаковках Кеплера скрываются разные многогранники. Начнём с любой сферы, возьмём её соседей и соединим их центры, чтобы получились вершины многогранника. В плотнейшей упаковке Кеплера любой сферы касаются 12 других, и из их центров получается кубооктаэдр с 12 вершинами и 14 гранями. Но Кеплер описывал и другую упаковку, на 8% менее плотную, в которой каждой сферы касается по 8 других, и ещё 6 стоят очень близко. Если соединить их центры, мы получим ромбический додекаэдр, с 14 вершинами и 12 гранями:

Обнаружив это, Кеплер начал поиски других «ромбических многогранников». В найденном им ромбическом додекаэдре ромбы состояли из пар равносторонних треугольников. Но к 1619 году Кеплер изучал и золотые ромбы — и нашёл ромбический тридцатигранник, после чего нарисовал в своей книге его красивое изображение, рядом с ромбическим додекаэдром:

Кеплер сразу же нашёл применение ромбическим многоугольникам: он хотел использовать их и куб, чтобы построить модель вложенных сфер, подходящую к орбитам четырёх лун Юпитера, открытых Галилеем в 1610-м.
Почему Кеплер не открыл ромбический шестидесятигранник? Думаю, он подошёл к нему довольно близко. Он изучал невыпуклые звёздчатые многогранники. Он рассматривал ромбические многогранники. Но, видимо, для его астрономических теорий хватило и ромбического тридцатигранника, после чего он прекратил поиски.
В итоге, конечно, законы Кеплера, не имеющие отношения к многогранником, стали главным вкладом в астрономию, пережившим его. Но работа Кеплера по многогранником — пусть и проведённая в рамках неверной физической теории — остаётся вечным вкладом в математику.
За последующие три столетия было найдено больше многогранников различной правильности — и к началу XX математикам было известно уже множество их видов:
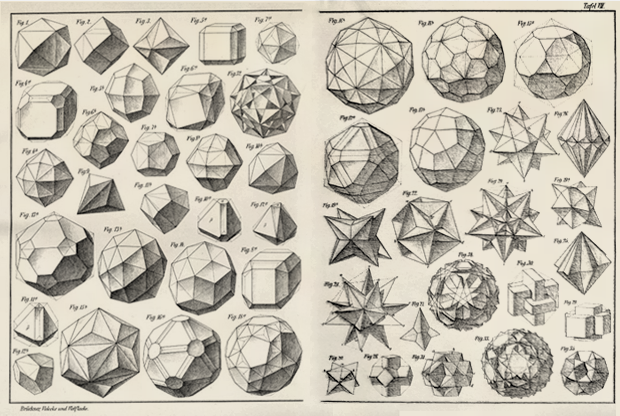
Но, насколько я могу судить, РШ среди них не было. Его открытие ждало работы Гельмута Ункельбаха. Он родился в 1910, защитил докторскую по математике в Мюнхенском университете в 1937 (хотя сначала изучал физику). Написал несколько работ по конформному отображению, и — возможно, благодаря изучению отображения многогранников, — в 1940 году опубликовал на немецком языке работу «Рёбро-симметричные многогранники».
Он пояснил, что его целью было всеобъемлющее исследование всех возможных многогранников, удовлетворявших особому новому определению правильности: все рёбра имеют одинаковую длину, и находятся в плоскости симметрии многогранника. Основным результатом работы стала таблица с 20 различными многогранниками такого свойства:
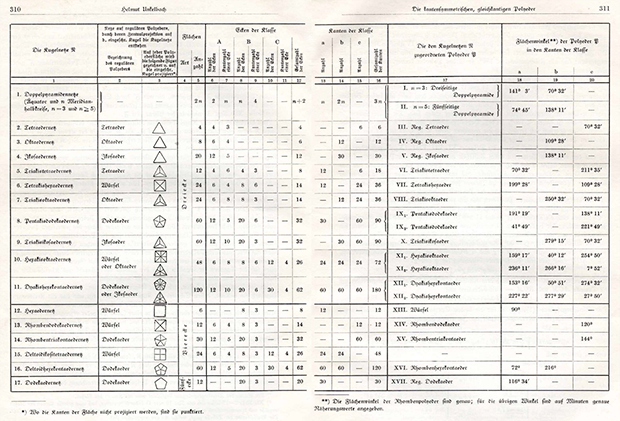
Кликабельно
Большая часть из них уже была известной. Но Ункельбах выделил три из них, которые считал новыми: два гекзакисоктаэдра (или дисдакисдодекаэдра), два гекзакисикосаэдра (или дисдакистриаконтаэдра) и то, что он назвал Rhombenhexekontaeder, или ромбический шестидесятигранник. И он явно считал РШ своим главным достижением, и включил фотографию его модели, сделанной им самим:

Как же он вывел РШ? Он начал с додекаэдра, и определил две его плоскости симметрии:
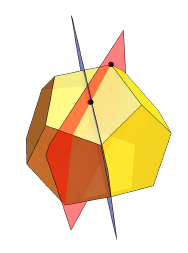
Затем разделил каждую из его граней:

Затем, по сути, выдавил центры каждой из граней на расстояние, равное обычному расстоянию до центра, умноженному на некое α:

Для α < 1 получавшиеся грани не пересекались. Но для большинства значений α их стороны не были равными. Это происходит только в определённом случае – когда итоговый многогранник точно совпадает с РШ.
Ункельбах считал свою работу 1940 года «разогревом» для более обширного исследования «k-симметричных многогранников» с менее жёсткими требованиями к симметрии. Но уже, конечно, чудом было то, что в Германии после начала Второй Мировой войны публиковался математический журнал — вскоре после этой публикации Ункельбаха призвали на фронт, где он несколько лет разрабатывал акустические торпеды для немецкого флота.
Больше работ по многогранникам он не публиковал, и умер в 1968. После годы он вернулся к конформному отображению, а ещё начал публиковаться по теории голосований, считая её ключом к созданию хорошо работавшей демократии, и думая, что математики были обязаны сделать так, чтобы люди начали её использовать.
Но, даже появившись в работе 1940 года, РШ мог прозябать там вечно, если бы в 1946 году некто Гарольд Скотт Макдональд Коксетер не написал небольшой обзор этой работы для относительно нового журнала American Mathematical Reviews. В его обзоре перечисляются многогранники, упомянутые в работе, как у натуралиста могут быть перечислены новые виды, открытые им в экспедиции. Главное, что он описал там и «примечательный ромбический шестидесятигранник», и упомянул, что «форма его граней совпадает с формой граней тридцатигранника, из которого он получен приданием звёздчатой формы».
Многогранники не были популярной темой в математике середины XX века, но Коксетер был их главным сторонником — и так или иначе был связан со всеми, кто их изучал. В 1948 году он опубликовал книгу «Правильные политопы». В ней систематически описываются различные семейства правильных многогранников, в частности, и великий звёздчатый тридцатигранник — по сути, содержащий в себе РШ:

Но в своей книге Коксетер не упоминает прямо РШ, и хотя он удостоился упоминаний некоторых любителей многогранников, РШ продолжал оставаться малоизвестным.
Квазикристаллы
Кристаллы всегда были важными примерами многогранников в природе. Но к XIX веку, когда всё больше признания получала атомная теория, учёные начали проводить всё более серьёзные исследования в области кристаллографии и расположения атомов в кристаллах. Многогранники стали часто появляться, в частности, в представлениях геометрии повторяющихся блоков атомов («ячеек») в кристаллах.
К 1850-му было известно, что таких геометрий может быть только 14 — среди них есть и основанная на ромбическом додекаэдре. Они примечательны наличием у них симметрий второго, третьего, четвёртого или шестого порядков — что, по сути, является следствием того факта, что пространство можно заполнить лишь определёнными многогранниками, точно так же, как двумерную плоскость могут заполнить только такие правильные многоугольники, как квадраты, треугольники и шестиугольники.
А что насчёт других, не кристаллических материалов — например, жидкостей или стекла? Людей ещё с начала XX века интересовала возможность наличия там хотя бы приблизительных симметрий пятого порядка. Правильными икосаэдрами заполнить пространство не получится, но, возможно, получится создать двадцатигранные участки пространства с небольшими промежутками между ними.
Этот вопрос оставался нерешённым до 1980-х, когда электронная дифракционная кристаллография на быстро охлаждаемом сплаве алюминия и марганца продемонстрировала наличие пятикратной симметрии. Теории достижения такой симметрии уже существовали, и через несколько лет появились также изображения, сделанные электронным микроскопом, на которых были видны частички, имеющие форму ромбического тридцатигранника:

И, пока люди представляли себе, как эти тридцатигранники могут совмещаться друг с другом, появился ещё и ромбический шестидесятигранник — в виде «дырки» в скоплении 12 ромбических тридцатигранников:

Сначала его называли 20-конечной звездой. Но затем его связали с описаниями в литературе по многогранником, и определили, как РШ.
Тем временем идея создавать предметы из ромбических элементов набирала всё больше популярности. К массовому увлечению присоединился Майкл Лонге-Хиггинс, океанограф и эксперт по формированию волн в океане, и в 1987 году запатентовал игрушку, основанную на ромбоэдрических элементах, из которой можно было собрать «звезду Кеплера» (РШ) или «шар Кеплера» (ромбический тридцатигранник):

И — хотя я узнал об этом только сейчас — ромбоэдрические блоки, которые мы в 2009 году рассматривали, как вариант для создания «Шипастиков», реально выпускала компания Dextro Mathematical Toys (Rhombo.com), работавшая на базе дома Лонге-Хиггинса в Сан-Диего.
Вопрос успешного заполнения пространства трёхмерными фигурами — или даже плоскости двумерными фигурами — довольно сложен. Ещё с 1960-х известно, что в общем случае задача о том, может ли определённый набор форм заполнить плоскость, является неразрешимой. (В принципе, можно проверить, могут ли 1000 этих форм быть составлены друг с другом, но чем больше форм мы будем рассматривать, тем больше вычислительных ресурсов это потребует).
Такие люди, как Кеплер, вероятно, предполагали, что если набор форм может заполнить плоскость, то это можно будет сделать в виде повторяющегося узора. Однако после того, как стало понятно, что в общем случае эта задача не решается, Роджер Пенроуз в 1974 году придумал две формы, которые могут заполнить плоскость без повторяющихся узоров. К 1976 году Пенроуз (и Роберт Амманн) придумали упрощённую версию этих форм:

И, да, эти формы имеют вид ромбов, хотя и не золотых. Но с углами в 36°, 144° и 72°, 108° они имеют 5-кратную и 10-кратную симметрию.
Этими ромбами нельзя выложить повторяющиеся узоры. Но, оказывается, что ими можно выложить узор, построенный систематическим вложенным способом:
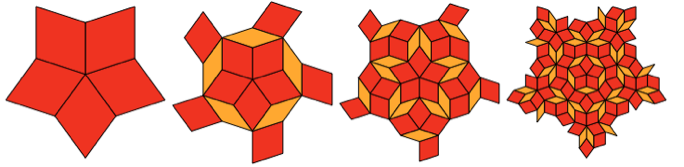
И, да, средняя часть 3-го шага очень похожа на уплощённого Шипастика. Но она не полностью совпадает с ним, внешние ромбы имеют немного другой формат.
Однако, близкая связь между ними всё же существует. Представьте, что мы начнём не с плоскости, а с половины трёхмерного ромбического тридцатигранника, состоящего из золотых ромбов:

Сверху он выглядит точно так же, как начало вложенной конструкции мозаики Пенроуза. Если продолжить этот процесс, мы получаем эту мозаику:

Если посмотреть на
