[Перевод] Имитируем иридисценцию: шейдер CD-ROM
Этот туториал посвящён иридисценции. В этом туториале мы исследуем саму природу света, чтобы понять и воссоздать поведение материала, создающего цветные отражения. Туториал предназначен для разработчиков игр на Unity, однако описанные в нём техники можно запросто реализовать на других языках, в том числе в Unreal и на WebGL.

Туториал будет состоять из следующих частей:
- Часть 1. Природа света
- Часть 2. Усовершенствуем радугу — 1
- Часть 3. Усовершенствуем радугу — 2
- Часть 4. Разбираемся с дифракционной решёткой
- Часть 5. Математика дифракционной решётки
- Часть 6. Шейдер CD-ROM: дифракционная решётка — 1
- Часть 7. Шейдер CD-ROM: дифракционная решётка — 2
Введение
Иридисценция — это оптическое явление, при котором объекты изменяют цвета при изменении угла освещения или угла обзора. Именно благодаря этому эффекту пузыри обладают такой широкой палитрой цветов.

Иридисценция также проявляется в луже пролитого бензина, на поверхности CD-ROM и даже на свежем мясе. Многие насекомые и животные используют иридисценцию для создания цветов без наличия соответствующих пигментов.

Так происходит потому, что иридисценция возникает вследствие взаимодействия света и микроскопических структур, которые находятся на поверхностях всех этих объектов. И дорожки CD-ROM, и чешуйки наружного скелета насекомого (см. изображения ниже) имеют тот же порядок величины длины волн света, с которым они взаимодействуют. На самом деле, иридисценция стала первым явлением, которое позволило раскрыть истинную волновую природу света. Мы не сможем объяснить и воспроизвести иридисценцию, не поняв сначала, что же такое свет, как он работает и как воспринимается глазом человека.


Природа света
Как и многие субатомные частицы, свет одновременно проявляет свойства частиц и волн. Довольно часто свет моделируют как первые или вторые. Для большинства применений свет можно рассматривать как созданный из триллионов отдельных частиц, называемых фотонами. Например, большинство шейдеров считает, что фотоны ведут себя как крошечные бильярдные шары и отражаются от объектов по тем углом, под которым столкнулись с ним (см. схему ниже).
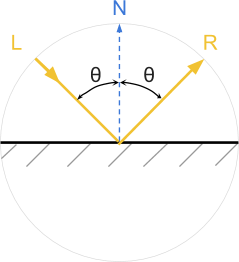
Но свет также можно смоделировать как волну. Физики знакомы с этой концепцией, однако разработчикам она известна не всегда. Так давайте же потратим немного времени на то, чтобы понять, что означает для света существование в виде волны.
Всем нам известны океанские волны. Каждая точка на поверхности океана имеет высоту. Чем выше она от среднего значения, тем выше волна. Если потревожить поверхность воды, волны начинают распространяться по океану, пока их энергия не рассеется.
Свет — это волна, но вместо того, чтобы измерять его как высоту на поверхности воды, он задаётся как энергия, которой обладает электромагнитное поле в нужной точке. В соответствии с этой моделью, свет — это возмущение электромагнитного поля, распространяющееся через пространство. Мы можем представить лампочку, или создающую волну, или испускающую в окружающее пространство множества фотонов.
Величина переносимой фотоном энергии определяет цвет света. Фотоны с низкой энергией воспринимаются как красный цвет; фотоны с высокой энергией воспринимаются как фиолетовый. Волны обладают свойством, аналогичным энергии частицы: длиной волны. Для интуитивного понимания можно сказать, что это расстояние между двумя пиками волны.
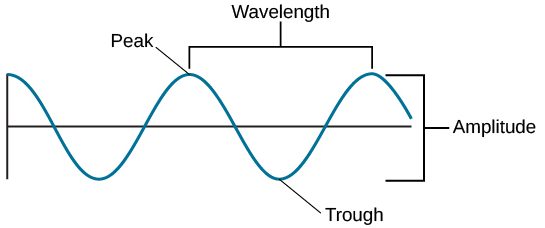
Свет всегда движется с одной скоростью (приблизительно 299 792 458 метров в секунду), то есть электромагнитные волны распространяются с одинаковой скоростью. Хотя их скорость постоянна, длина волн может быть разной. Фотоны с высокой энергией — это волны с короткой длиной. Именно длина волны света в конце концов определяет его цвет.
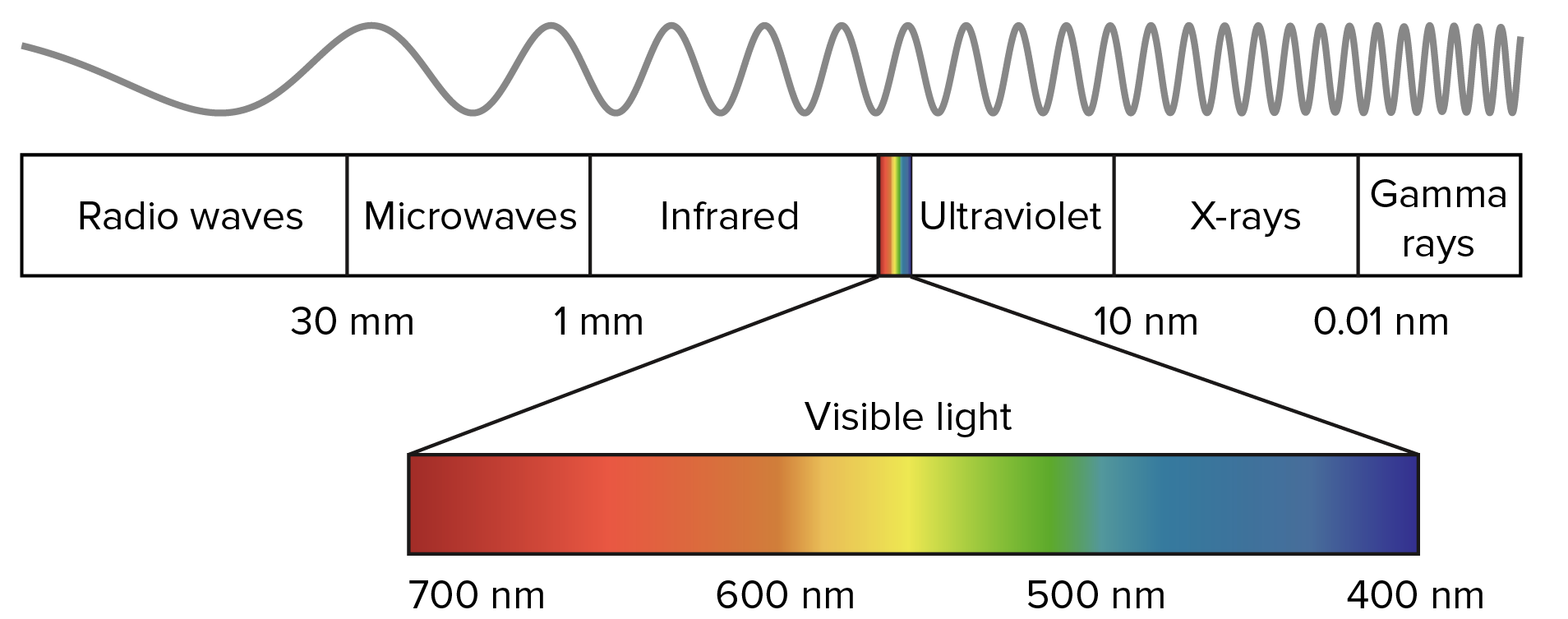
Как вы видите на схеме выше, глаз человека может воспринимать фотоны с длиной волны в интервале примерно от 700 нанометров до 400 нанометров. Нанометр — это миллиардная часть метра.
Что дальше?
После этого краткого введения в оставшейся части туториала мы сосредоточимся на понимании иридисценции и её реализации в Unity.
- Усовершенствуем радугу. Как сказано выше, разные длины волн света воспринимаются человеческим глазом как разные цвета. В следующих двух частях мы разберёмся с тем, как связать эти длины волн с цветами RGB. Этот шаг необходим для воссоздания иридисцентных отражений с высокой степенью точности. В этих частях я также представлю новый подход, который будет и физически точным, и эффективным с точки зрения вычислений.
- Дифракционная решётка. В частях 4 и 5 этого туториала мы рассмотрим дифракционную решётку. Это техническое название одного из эффектов, заставляющих материалы демонстрировать иридисцентные отражения. Несмотря на свою «техничность», выведенное уравнение, управляющее этим оптическим явлением, будет очень простым. Если вас не интересует математика дифракционной решётки, то можете пропустить часть 5.
- Шейдер CD-ROM. Ядро этого туториала — реализация шейдера CD-ROM. В нём для реализации дифракционной решётки в Unity будут использоваться знания, собранные в предыдущих частях. Он является расширением стандартного поверхностного шейдера (Standard Surface shader) Unity 5; что делает этот эффект и физически правильнмы, и фотореалистичным. Приложив небольшие усилия, вы сможете изменить его так, чтобы он соответствовал другим типам иридисцентных отражений, основанных на дифракционной решётке.
Подведём итог
С этой части мы начали туториал по иридисценции. В оставшейся части статьи мы исследуем способы симуляции и реализации иридисцентных отражений на различных материалах, от пузырей до CD-ROMs, и от разлитого бензина до насекомых.
Часть 2. Усовершенствуем радугу — 1.
Наше путешествие в мир фотореализма требует от нас понимания не только того, как работает свет, но и как мы воспринимаем цвета. Сколько цветов есть в радуге? Почему розовый в них не входит? Вот только некоторые из вопросов, которые мы рассмотрим в этой части.

Введение
В этой части мы познакомимся в наиболее популярными техниками, используемыми в компьютерной графике для воссоздания цветов радуги. Хотя это может казаться бесполезным занятием, на самом деле оно имеет очень практическое применение. Каждый цвет радуги соответствует определённой длине волны света. Такое соответствие позволит нам симулировать физически достоверные отражения.
В следующей части, «Усовершенствуем радугу — 2», мы введём новый подход, который очень хорошо оптимизирован для шейдеров и при этом создаёт наилучшие на данный момент результаты (см. ниже).
Сравнение WebGL-версий всех рассмотренных в этом туториале техник можно посмотреть в Shadertoy.
Восприятие цветов
Сетчатка — это часть глаза, распознающая свет. В ней есть клетки-колбочки, способные передавать сигналы в мозг при распознавании определённых длин волн света. Свет — это волна в электромагнитном поле, поэтому колбочки работают по тем же принципам, которые позволяют нам распознавать радиоволны. Де-факто колбочки являются крошечными антеннами. Если вы изучали электронику, то должны знать, что длина антенны связана с улавливаемой ею длиной волны. Именно поэтому в глазе человека есть три разных типа колбочек: короткие, средние и длинные. Каждый тип специализируется в распознавании определённого интервала длин волн.
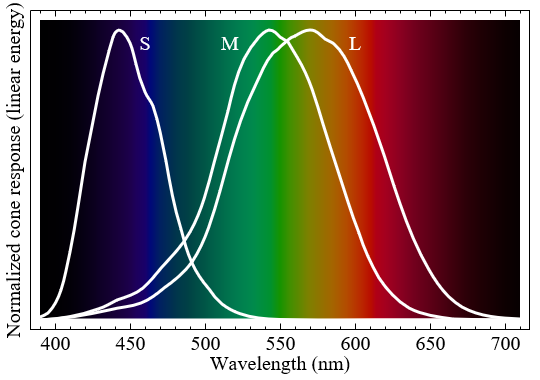
На графике выше показано, насколько каждый тип колбочек реагирует на разные длины волн. Когда один из этих типов колбочек активируется, мозг интерпретирует его сигнал как цвет. Несмотря на то, что такое часто говорят, короткие, средние и длинные колбочки не соответствуют определённым цветам. Если точнее, каждый тип по-разному реагирует на разные цветовые диапазоны.
Неверно будет считать, что короткие, средние и длинные колбочки распознают синий, зелёный и красный цвета. Несмотря на это, во многих учебниках (и даже в шейдерах!) принимается такое допущение для создания относительно приемлемой аппроксимации этого довольно сложного явления.
Спектральный цвет
Если мы хотим воссоздать физические явления, которые делают возможной иридисценцию, то нам нужно переосмыслить способ хранения и обработки цветов в компьютере. Когда мы создаём в Unity (или любом другом игровом движке) источник света, то можем задавать его цвет как смешение трёх основных компонентов: красного, зелёного и синего. Хотя сочетанием красного, зелёного и синего цветов действительно можно создать все видимые цвета, на самом фундаментальном уровне свет работает иначе.
Источник света можно смоделировать как постоянный поток фотонов. Фотоны, несущие разные величины энергии, воспринимаются нашим глазом как разные цвета. Однако «белого фотона» не существует. Это сумма множества фотонов, каждый из которых имеет разную длину волны, что придаёт свету белый цвет.
Чтобы двигаться дальше, нам нужно поговорить о самих «стоительных блоках» света. Когда мы говорим о «длинах волн», то стоит думать о конкретных цветах радуги. В этой части мы покажем различные подходы, реализующие данную связь. В результате мы хотим получить функцию, которая для заданного цвета возвращает воспринимаемый цвет:
fixed3 spectralColor (float wavelength);
В оставшейся части поста мы будем выражать длины волн в нанометрах (миллиардных частях метра). Глаз человека может воспринимать свет в диапазоне от 400 нм до 700 нм. Длины волн за пределами этого диапазона существуют, но не воспринимаются как цвета.
«Не существует уникального соответствия между длиной волны и значениями RGB. Цвет — это удивительное сочетание физики и человеческого восприятия».
Поиск окончательно верного соответствия длин волн и цветов неизбежно обречён на провал. Природа света объективна, а наше восприятие — нет. Колбочки, воспринимающие определённые длины волн видимого спектра, имеют значительные вариации у разных людей. Даже если предположить, что все колбочки работают одинаково и постоянно для всех людей, их распределение и количество в сетчатке в основном случайны. Никакие две сетчатки не одинаковы, даже у одного человека.
Наконец, восприятие цвета зависит от того, как эти входные данные воспринимает мозг. Благодаря этому возникают различные оптические иллюзии и нейроадаптации, которые делают восприятие цветов уникальным и истинно личностным опытом.
Спектральная карта
На рисунке ниже показано, как глаз человека воспринимает волны длиной от 400 нанометров (синие) до 700 нанометров (красные).

Легко увидеть, что распределение цветов в видимом спектре очень нелинейно. Если мы нанесём на график для каждой длины волны соответствующие компоненты R, G и B воспринимаемого цвета, то в результате получим нечто подобное:

Не существует простой функции, которая может полностью описать эту кривую. Простейшим и наименее затратным подходом реализации будет использование этой текстуры в шейдере как средства привязки длин волн к цветам.
Первое, что нужно сделать — обеспечить шейдеру доступ к новой текстуре. Мы можем сделать это, добавив в блок Properties нового шейдера свойство текстуры.
// Свойства
Properties
{
...
_SpectralTex("Spectral Map (RGB)",2D) = "white" {}
...
}
// Код шейдера
SubShader
{
...
CGPROGRAM
...
sampler2D _SpectralTex;
...
ENDCG
...
}
Наша функция spectralColor просто преобразует длины волн в интервале [400,700] в UV-координаты в интервале [0,1]:
fixed3 spectral_tex (float wavelength)
{
// длина волны: [400, 700]
// u: [0, 1]
fixed u = (wavelength -400.0) / 300.0;
return tex2D(_SpectralTex, fixed2(u, 0.5));
}
В нашем конкретном случае нам не нужно принудительно ограничивать длины волн интервалом [400, 700]. Если спектральная текстура импортируется с Repeat: Clamp, все значения за пределами этого интервала будут автоматически иметь чёрный цвет.
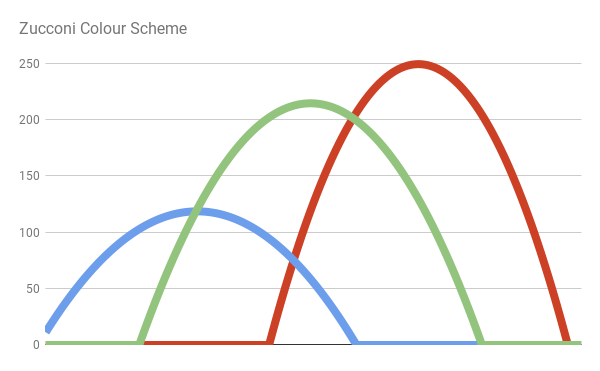
Цветовая схема JET
Сэмплирование текстуры может показаться хорошей идеей. Однако оно может значительно замедлить шейдер. Мы увидим, насколько это критично, в части про иридисценцию на CD-ROM, где каждому пикселю потребуются несколько сэмплов текстуры.
Существует несколько функций, аппроксимирующих распределения цветов светового спектра. Вероятно, одной из самых простых является цветовая схема JET. Эта цветовая схема по умолчанию используется в MATLAB, и изначально она была выведена Национальным центром суперкомпьютерных приложений для лучшей визуализации симуляций струй жидкости в астрофизике.

Цветовая схема JET является сочетанием трёх разных кривых: синей, зелёной и красной. Это чётко видно при разбиении цвета:
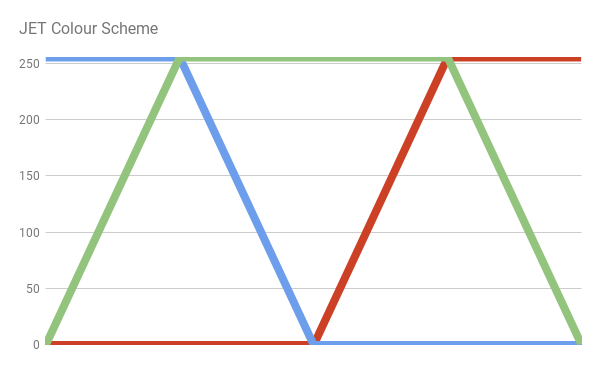
Мы с лёгкостью можем самостоятельно реализовать цветовую схему JET, написав уравениня линий, составляющих представленную выше схему.
// Цветовая схема MATLAB Jet
fixed3 spectral_jet(float w)
{
// w: [400, 700]
// x: [0, 1]
fixed x = saturate((w - 400.0)/300.0);
fixed3 c;
if (x < 0.25)
c = fixed3(0.0, 4.0 * x, 1.0);
else if (x < 0.5)
c = fixed3(0.0, 1.0, 1.0 + 4.0 * (0.25 - x));
else if (x < 0.75)
c = fixed3(4.0 * (x - 0.5), 1.0, 0.0);
else
c = fixed3(1.0, 1.0 + 4.0 * (0.75 - x), 0.0);
// Ограничиваем компоненты цвета интервалом [0,1]
return saturate(c);
}
Значения R, G и B получившегося цвета ограничены интервалом [0,1] с помощью функции Cg saturate. Если для камеры выбран режим HDR (High Dynamic Range Rendering), это необходимо, чтобы избежать наличия цветов с компонентами больше единицы.
Стоит заметить, что если вы хотите строго придерживаться цветовой схемы JET, то значения за пределами видимого диапазона не будут чёрными.
Цветовая схема Брутона
Ещё одним подходом к преобразованию длин волн в видимые цвета является схема, предложенная Дэном Брутоном в статье «Approximate RGB values for Visible Wavelengths». Аналогично тому, что происходит в цветовой схеме JET, Брутон начинает с аппроксимированного распределения воспринимаемых цветов.
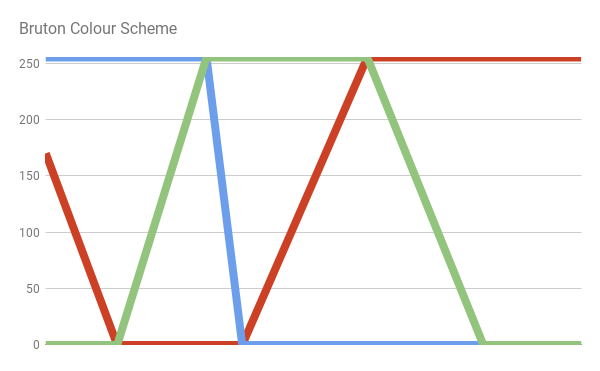
Однако его подход лучше аппроксимирует активность длинных колбочек, что приводит к более сильному оттенку фиолетового в нижней части видимого спектра:

Такой подход преобразуется в следующий код:
// Дэн Брутон
fixed3 spectral_bruton (float w)
{
fixed3 c;
if (w >= 380 && w < 440)
c = fixed3
(
-(w - 440.) / (440. - 380.),
0.0,
1.0
);
else if (w >= 440 && w < 490)
c = fixed3
(
0.0,
(w - 440.) / (490. - 440.),
1.0
);
else if (w >= 490 && w < 510)
c = fixed3
( 0.0,
1.0,
-(w - 510.) / (510. - 490.)
);
else if (w >= 510 && w < 580)
c = fixed3
(
(w - 510.) / (580. - 510.),
1.0,
0.0
);
else if (w >= 580 && w < 645)
c = fixed3
(
1.0,
-(w - 645.) / (645. - 580.),
0.0
);
else if (w >= 645 && w <= 780)
c = fixed3
( 1.0,
0.0,
0.0
);
else
c = fixed3
( 0.0,
0.0,
0.0
);
return saturate(c);
}Цветовая схема Bump
Цветовые схемы JET и Брутона используют прерывные функции. Поэтому в них создаются довольно резкие цветовые вариации. Более того, за пределами видимого диапазона они не становятся чёрным цветом. В книге «GPU Gems» эта проблема решается заменой резких линий предыдущих цветовых схем на гораздо более плавные изгибы (bumps). Каждый изгиб является обычной параболой вида . А конкретнее
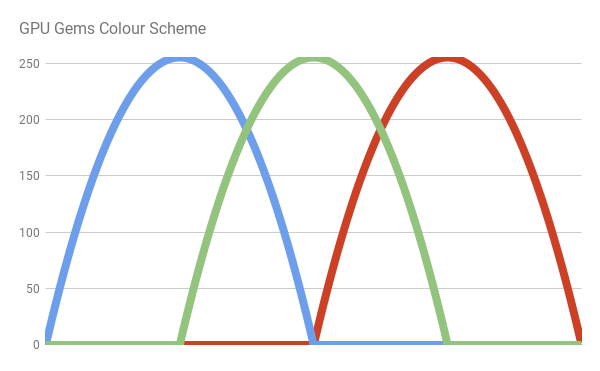
Мы можем написать следующий код:
// GPU Gems
inline fixed3 bump3 (fixed3 x)
{
float3 y = 1 - x * x;
y = max(y, 0);
return y;
}
fixed3 spectral_gems (float w)
{
// w: [400, 700]
// x: [0, 1]
fixed x = saturate((w - 400.0)/300.0);
return bump3
( fixed3
(
4 * (x - 0.75), // Red
4 * (x - 0.5), // Green
4 * (x - 0.25) // Blue
)
);
}
Дополнительное преимущество этой цветовой схемы заключается в том, что в ней не используются сэмплы текстур и ветвление, что делает её одним из лучших решений, если вы предпочитаете скорость, а не качество. В конце этого туториала я покажу пересмотренную версию этой цветовой схемы, которая обеспечивает бОльшую скорость, при этом сохраняя высокую чёткость цветов.
Цветовая схема Spektre
Одной из самых точных цветовых схем является схема, созданная пользователем Stack Overflow Spektre. Он объясняет свою методологию в посте RGB values of visible spectrum, где он сэмплирует синий, зелёный и красный компоненты вещественных данных из солнечного спектра. После чего он заполняет отдельные интервалы простыми функциями. Результат показан на следующей схеме:
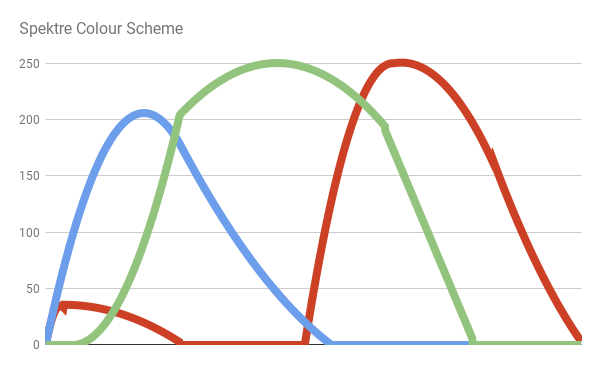
Что даёт нам:

А вот как выглядит код:
// Spektre
fixed3 spectral_spektre (float l)
{
float r=0.0,g=0.0,b=0.0;
if ((l>=400.0)&&(l<410.0)) { float t=(l-400.0)/(410.0-400.0); r= +(0.33*t)-(0.20*t*t); }
else if ((l>=410.0)&&(l<475.0)) { float t=(l-410.0)/(475.0-410.0); r=0.14 -(0.13*t*t); }
else if ((l>=545.0)&&(l<595.0)) { float t=(l-545.0)/(595.0-545.0); r= +(1.98*t)-( t*t); }
else if ((l>=595.0)&&(l<650.0)) { float t=(l-595.0)/(650.0-595.0); r=0.98+(0.06*t)-(0.40*t*t); }
else if ((l>=650.0)&&(l<700.0)) { float t=(l-650.0)/(700.0-650.0); r=0.65-(0.84*t)+(0.20*t*t); }
if ((l>=415.0)&&(l<475.0)) { float t=(l-415.0)/(475.0-415.0); g= +(0.80*t*t); }
else if ((l>=475.0)&&(l<590.0)) { float t=(l-475.0)/(590.0-475.0); g=0.8 +(0.76*t)-(0.80*t*t); }
else if ((l>=585.0)&&(l<639.0)) { float t=(l-585.0)/(639.0-585.0); g=0.82-(0.80*t) ; }
if ((l>=400.0)&&(l<475.0)) { float t=(l-400.0)/(475.0-400.0); b= +(2.20*t)-(1.50*t*t); }
else if ((l>=475.0)&&(l<560.0)) { float t=(l-475.0)/(560.0-475.0); b=0.7 -( t)+(0.30*t*t); }
return fixed3(r,g,b);
}Заключение
В этой части мы рассмотрели некоторые самые распространённые техники для генерирования в шейдере похожих на радугу паттернов. В следующей части я познакомлю вас с новым подходом к решению этой задачи.
| Название | Градиент |
| JET |  |
| Bruton |  |
| GPU Gems |  |
| Spektre |  |
| Zucconi |  |
| Zucconi6 |  |
| Видимый спектр |  |
Часть 3. Усовершенствуем радугу — 2.
Введение
В предыдущей части мы проанализировали четыре различных способа преобразования длин волн видимого диапазона электромагнитного спектра (400–700 нанометров) в соответствующие им цвета.
В трёх из этих решений (JET, Bruton и Spektre) активно используются конструкции if. Для C# это стандартная практика, однако в шейдере ветвление является плохим подходом. Единственным подходом, в котором не используется ветвление, является рассмотренный в книге GPU Gems. Однако он не обеспечивает оптимальную аппроксимацию цветов видимого спектра.
| Название | Градиент |
| GPU Gems |  |
| Видимый спектр |  |
В этой части я расскажу про оптимизированную версию цветовой схемы, описанной в книге GPU Gems.
Цветовая схема «Bump»
Исходная цветовая схема, изложенная в книге GPU Gems, для воссоздания распределения компонентов R, G и B цветов радуги использует три параболы (называемые автором bumps).

Каждый bump описывается следующим уравнением:
в диапазоне [400, 700] сопоставляется с нормализованным значением
в интервале [0,1]. Затем компоненты R, G и B видимого спектра задаются следующим образом:
Все численные значения подобраны автором экспериментально. Однако вы видите, насколько плохо они соответствуют истинному распределению цветов.

Оптимизация качества
В первом решении, к которому пришёл я, использовались точно такие же уравнения, что и в цветовой схеме GPU Gems. Однако я оптимизировал все численные значения, так что конечный диапазон цветов соответствует, насколько это возможно, настоящим цветам из видимого спектра.
Результат сводится к следующему решению:
И приводит к гораздо более реалистичному результату:
| Название | Градиент |
| GPU Gems |  |
| Zucconi |  |
| Видимый спектр |  |
Как и исходное решение, новый подход не содержит ветвления. Поэтому он идеально подходит для шейдеров. Код имеет следующий вид:
// На основе кода из GPU Gems
// Оптимизовано Аланом Цуккони
inline fixed3 bump3y (fixed3 x, fixed3 yoffset)
{
float3 y = 1 - x * x;
y = saturate(y-yoffset);
return y;
}
fixed3 spectral_zucconi (float w)
{
// w: [400, 700]
// x: [0, 1]
fixed x = saturate((w - 400.0)/ 300.0);
const float3 cs = float3(3.54541723, 2.86670055, 2.29421995);
const float3 xs = float3(0.69548916, 0.49416934, 0.28269708);
const float3 ys = float3(0.02320775, 0.15936245, 0.53520021);
return bump3y ( cs * (x - xs), ys);
}Вот параметры, необходимые для воссоздания моих результатов:
- Algorithm: L-BFGS-B
- Tolerance:
- Iterations:
- Weighted MSE:
- Fitting
- Image: Linear Visible Spectrum
- Wavelength range: from
to
- Range resized to:
pixels
- Исходное решение:
- Конечное решение:
Усовершенствуем радугу
Если внимательнее присмотреться к распределению цветов в видимом спектре, то мы заметим, что параболы на самом деле не могут повторить кривые цветов R, G и B. Немного лучше будет использовать шесть парабол вместо трёх. Привязав к каждому основному компоненту по два bump, мы получим гораздо более правильную аппроксимацию. Разница очень заметна в фиолетовой части спектра.

Разница хорошо заметна в фиолетовой и оранжевой частях спектра:
| Название | Градиент |
| Zucconi |  |
| Zucconi6 |  |
| Видимый спектр |  |
Вот как выглядит код:
// На основе кода из GPU Gems
// Оптимизировано Аланом Цуккони
fixed3 spectral_zucconi6 (float w)
{
// w: [400, 700]
// x: [0, 1]
fixed x = saturate((w - 400.0)/ 300.0);
const float3 c1 = float3(3.54585104, 2.93225262, 2.41593945);
const float3 x1 = float3(0.69549072, 0.49228336, 0.27699880);
const float3 y1 = float3(0.02312639, 0.15225084, 0.52607955);
const float3 c2 = float3(3.90307140, 3.21182957, 3.96587128);
const float3 x2 = float3(0.11748627, 0.86755042, 0.66077860);
const float3 y2 = float3(0.84897130, 0.88445281, 0.73949448);
return
bump3y(c1 * (x - x1), y1) +
bump3y(c2 * (x - x2), y2) ;
}
Нет никаких сомнений, что spectral_zucconi6 обеспечивает более качественную аппроксимацию цветов без использования ветвления. Если для вас важна скорость, то можно использовать упрощённую версию алгоритма — spectral_zucconi.
Подводим итог
В этой части мы рассмотрели новый подход к генерированию в шейдерах похожих на радугу паттернов.
| Название | Градиент |
| JET |  |
| Bruton |  |
| GPU Gems |  |
| Spektre |  |
| Zucconi |  |
| Zucconi6 |  |
| Видимый спектр |  |
Часть 4. Разбираемся с дифракционной решёткой
В первой части туториала мы познакомились с двойственной природой света, который проявляет свойства волн и частиц. В этой части мы увидим, почему оба эти два аспекта необходимы для возникновения иридисценции.
Отражения: свет и зеркала
В научной литературе часто упоминается луч света как способ указания пути, проходимого фотонами в пространстве и взаимодействия с объектами. В большинстве моделей затенения свет воспринимается как созданный из однородных частиц, ведущих себя как идеальные бильярдные шары. В общем случае, когда луч света сталкивается с поверхностью, он отражается от неё под тем же углом отклонения. Такие поверхности ведут себя как идеальные зеркала, полностью отражая свет.

Объекты, отрендеренные в такой технике, походят на зеркала. Более того, если свет падает с направления L, то наблюдатель может увидеть его только тогда, когда смотрит с направления R. Такой тип отражения также называется specular, что означает «зеркалоподобный».
В реальном мире большинство объектов отражает свет другим способом, называемым рассеянным (diffuse). Когда луч света падает на рассеивающую поверхность, он более-менее равномерно рассеивается во всех направлениях. Это придаёт объектам равномерную рассеянную расцветку.
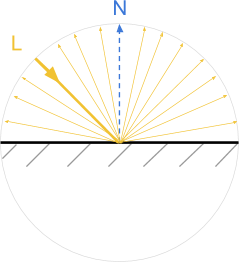
В большинстве современных движков (наподобие Unity и Unreal) эти два поведения моделируются с помощью разных наборов уравнений. В своём предыдущем туториале Physically Based Rendering and Lighting Models я объяснял модели отражаемостиЛамберта и Блинна-Фонга, которые используются соответственно для рассеянных и зеркальных отражений.
Несмотря на то, что они выглядят по-разному, рассеянное отражение можно объяснить через зеркальное. Никакая поверхность не является совершенно плоской. Можно смоделировать грубую поверхность как созданную из крошечных зеркал, каждое из которых полностью характеризуется зеркальной отражаемостью. Наличие таких микрограней приводит к рассеянию лучей во всех направлениях.
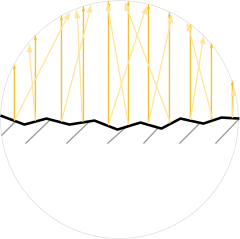
Разнонаправленность таких микрограней часто моделируется физически точными шейдерами с помощью таких свойств, как Smoothness (гладкость) или Roughness (шероховатость). Подробнее об этом можно прочитать на странице справки Unity, объясняющей свойство Smoothness стандартного шейдера движка.

И в самом деле, за этот эффект ответственно кое-что ещё. Диффузный компонент поверхности также возникает из вторичного источника: преломления. Свет может проникать сквозь поверхность объекта, отражаться внутри него и выходить под другим углом (см. рисунок выше). Это значит, что какой-то процент всего падающего света будет повторно излучаться поверхностью материала в любой произвольной точке и под любым углом. Такое поведение часто называют подповерхностным рассеянием (subsurface scattering) и вычисления для его симуляции часто бывают очень затратны.
Подробнее об этих эффектах (и их симуляции) можно прочитать в статье Basic Theory of Physically Based Rendering компании Marmoset.
Свет как волна
Очень удобно моделировать лучи света так, как будто они состоят из частиц. Однако это не позволит нам воссоздать поведение, которое демонстрирует множество материалов, в том числе и иридисценцию. Некоторые явления можно полностью понять только в том случае, если принять тот факт, что свет в определённых условиях ведёт себя как волна.
Большинство шейдеров работает со светом как с частицами. Результатом этого огромного упрощения становится то, что подвергается аддитивной композиции. Если два луча достигают наблюдателя, то их яркость просто складывается. Чем больше лучей испускает поверхность, тем она ярче.
В реальном мире это не так. Если два луча света достигают наблюдателя, то конечный цвет зависит от того, как их волны взаимодействуют друг с другом. В представленной ниже анимации показано, как две простые синусоидальные волны могут усиливать или <
