[Перевод] Если нарисуем такие графы, сможем навсегда изменить компьютеры
 Инженеры могли бы использовать этот прорыв в теории графов для разработки невероятно эффективных квантовых компьютерных микросхем.
Инженеры могли бы использовать этот прорыв в теории графов для разработки невероятно эффективных квантовых компьютерных микросхем.Доцент кафедры информатики в Копенгагенском университете Джейкоб Холм просматривал доказательства из научной статьи, опубликованной в Интернете в октябре 2019 года им и его коллегой Евой Ротенберг (доцентом кафедры прикладной математики и информатики Датского технического университета), и обнаружил, что их результаты невольно дали решение многовековой проблемы графов.
Холм был рад, что никто не нашёл решение раньше. «Это был самый подходящий момент, чтобы крикнуть «Эврика», — сказал он, — внезапно это показалось очевидным».
Холм и Ротенберг пытались найти оптимальный способ определения того, является ли граф «плоским», то есть можно ли его нарисовать плоским на поверхности без пересечения линий (плоские рисунки графа также называются «вложениями»).
Говоря очень прямо, мы формально определили, почему определённое начертание ужасно
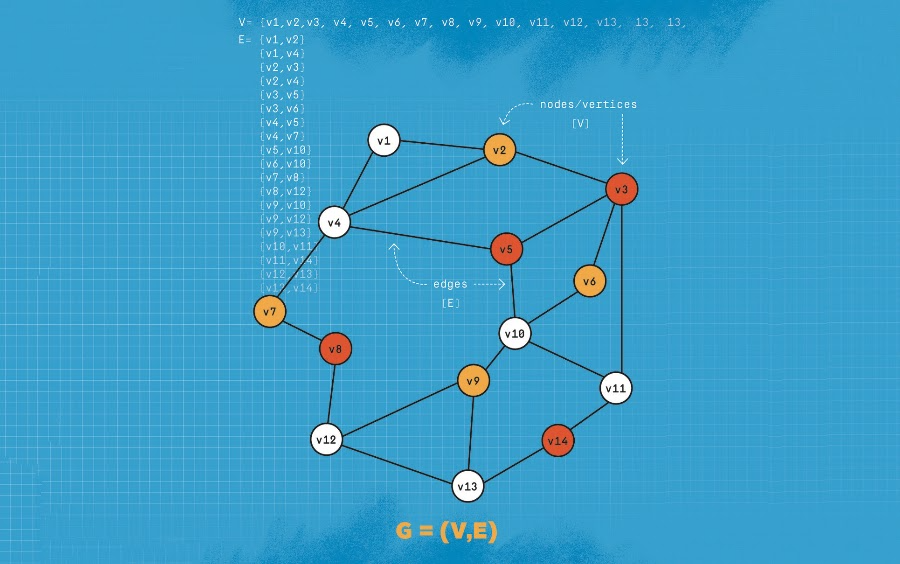
В представлении математиков граф часто отличается от того, чему большинство из нас учили в школе. Граф в данном случае — это любое количество точек, называемых узлами, связанных попарными связями, называемыми ребрами. Другими словами, ребро — это кривая, соединяющая два узла. В соответствии с этим определением граф может представлять всё — от сложной проводки внутри компьютерной микросхемы до дорожной карты города, на которой улицы Манхэттена могут быть представлены в виде рёбер, а их пересечения — в виде узлов. Графы изучаются в теории графов.
Инженерам необходимо найти планарность в графе, когда, например, они проектируют компьютерную микросхему без перекрещивающихся проводников. Однако оценить планарность при добавлении и удалении рёбер сложно, не рисуя график самостоятельно и стараясь избежать пересечения линий (см. «Задачу «Домики и колодцы» ниже, которая впервые была опубликована в выпуске The Strand Magazine в 1913 году).
По словам Ротенберг, оценка планарности ещё более усложняется в больших графах с большим количеством узлов и рёбер. Это не абстрактная проблема. Квантовые компьютерные микросхемы, например, — передовые устройства, и поиск эффективных способов оценки их планарности без потери времени и денег имеет решающее значение для их разработки.
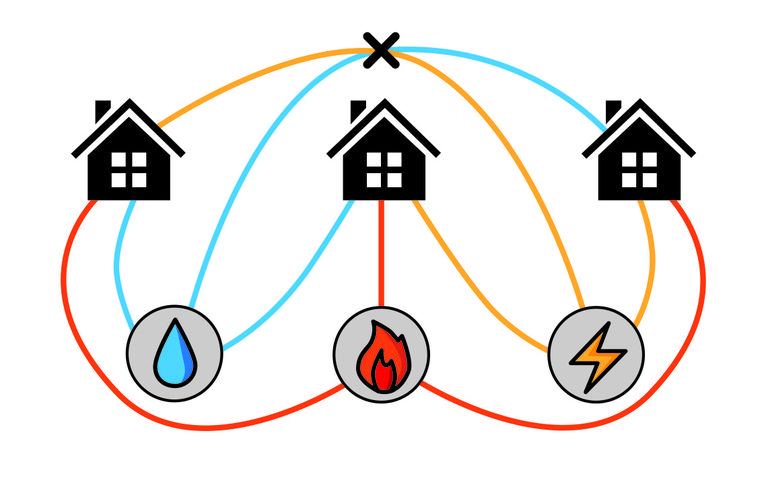 Решите задачу «Домики и колодцы».
Решите задачу «Домики и колодцы».Каждому из этих трёх домов нужен доступ к воде, газу и электричеству, но по соображениям безопасности линии, соединяющие коммунальные службы и дома, не могут пересекаться. Возьмите лист бумаги, нарисуйте эту задачу и попытайтесь соединить все три дома со всеми тремя коммунальными службами, так, чтобы линии не пересекались. Если вы думаете, что получили правильный ответ, проверьте его внизу этой страницы.
В оригинальной статье 2019 года, опубликованной на сервере препринтов arXiv, где исследования часто впервые выходят в свет ещё до рецензирования, Холм и Ротенберг классифицировали тип вложения, который называется «сбалансированным» или «хорошим» вложением.
Холм объясняет, что эти хорошие вложения «имеют тенденцию «уравновешивать» [временные] затраты на вставку рёбер, так что никакая возможная вставка рёбер не стоит слишком дорого по сравнению с остальными». Эта концепция заимствована для деревьев сбалансированных решений в информатике, которые разрабатываются с равномерно распределёнными ветвями для минимизации времени поиска. Другими словами, к хорошим вложениям легче добавлять новые рёбра, не нарушая планарность.
«Если посмотреть на него, — говорит Холм, — «хорошее» вложение окажется простым, незамысловатым. Обычный пример — это так называемый лестничный граф. Сбалансированное вложение этого графа выглядит в точности как лестница». Однако Холм сказал следующее: «В несбалансированном вложении это трудно распознать».
С субъективной точки зрения, лестничный граф — «хороший», а его альтернативы — «плохие», но Холм и Ротенберг сформулировали в своей статье, почему эти утверждения математически верны. «Говоря очень прямо, мы формально определили, почему какое-то начертание ужасно», — рассказывает Ротенберг, имея в виду плохое вложение. В то время оба учёных не понимали, что их класс хороших вложений сыграл существенную роль в ускорении процесса динамического тестирования планарности.
Когда требуется добавить новое ребро в планарный граф, возможны два сценария: способ безопасного добавления ребра существует, возможно, после изменения начертания, или же начертания, допускающего новое ребро, не существует. Однако в некоторых случаях вложение самого графа может скрывать способ планарной вставки ребра. Чтобы выявить такие альтернативные способы, математики «переворачивают» вложение, изменяя его ориентацию и сохраняя при этом его математическую тождественность, поскольку связи между соединёнными узлами и рёбрами не изменялись.
Такие перевороты могут позволить добавить между двумя недавно упорядоченными узлами рёбра, которые в противном случае нарушили бы планарность. Холм и Ротенберг обнаружили, что перевороты, приводящие к успешной вставке и удалению рёбер, как правило, попадают в их класс так называемых хороших вложений. Точно так же эти хорошие вложения требуют меньшего количества переворотов для успешного добавления новых рёбер. Беспроигрышный вариант.
Учёные предложили множество приложений своей работы, включая проектирование микросхем, поверхностные сетки и дорожные сети, но Ротенберг признала: «Что привлекает нас в этой проблеме, так это её загадочный характер». Учёные осторожно подходят к прогнозированию большего числа коммерческих приложений, поскольку выполнение «переворотов» в реальных конструкциях графов может оказаться сложной задачей.
Однако они считают, что их подход к оценке динамических графов (то есть графов, которые изменяются посредством вставок и удалений) может повлиять на подход математиков к аналогичным задачам. По сути, оценивая планарность, их алгоритм также отслеживает и вычисляет изменения в графах, выполняя так называемый «регрессивный анализ», — говорит Ротенберг.
Сбор даже таких данных — не излишество. По утверждению Ротенберг, их решение показывает, что регрессионный анализ может иметь алгоритмические приложения, помимо того, что он «интересен сам по себе», потому что здесь он привёл к эффективному тесту на планарность.
По её словам, анализ динамических математических концепций — это «открытая область», но в ней заложен потенциал. Возможно, такие прорывы уже произошли — они просто скрыты в процессе.
Решение задачи «Домики и колодцы»: на самом деле эту задачу в двухмерном пространстве решить невозможно.
Узнайте подробности, как получить Level Up по навыкам и зарплате или востребованную профессию с нуля. Скидка только для хабравчан 50% по промокоду HABR.
Другие профессии и курсыПРОФЕССИИ
КУРСЫ
