[Перевод] Deep Learning в иллюстрациях: Рекуррентные нейронные сети
Наглядное руководство по внутреннему устройству рекуррентных нейронных сетей и функции активации Softmax
Рад приветствовать вас в очередной части нашего иллюстрированного погружения в Deep Learning! Сегодня мы будем разбираться в рекуррентных нейронных сетях. Мы будем обсуждать уже хорошо знакомые нам понятия, такие как входы, выходы и функции активации, но с неожиданным сюжетным поворотом! И если это ваша первая остановка в этом увлекательном путешествии, то я настоятельно рекомендую вам сперва прочитать предыдущие статьи, особенно части 1 и 2.
Рекуррентные нейронные сети (Recurrent Neural Networks, RNN) — это уникальные модели, специально разработанные для решения задач обработки серии событий во времени или последовательных пространственных цепочек, где следующая позиция зависит от предыдущего состояния.
Давайте разберемся, что из себя могут представлять такие задачи, на простом примере из курса MIT. Представьте себе мяч в определенный момент времени tn.

Если нас просят предсказать направление движения мяча, не давая никакой дополнительной информации, то это игра в угадайку, ведь он может двигаться в любом направлении.

Но что, если у нас будут данные о предыдущих положениях мяча?

Теперь мы можем с уверенностью предсказать, что мяч продолжит двигаться вправо.

Этот сценарий прогнозирования, где ответ сильно зависит от предыдущих данных, мы называем последовательной задачей. Такие последовательные задачи встречаются повсюду: от прогнозирования завтрашней температуры на основе данных за предыдущие дни (или даже годы) до различных языковых моделей, включая анализ тональности, распознавание именованных сущностей, машинный перевод и распознавание речи. Сегодня мы займемся определением тональности текста — простым примером последовательной задачи.
В рамках определения тональности мы берем фрагмент текста и определяем, позитивная или негативная у него эмоциональная окраска. Сегодня мы построим RNN, которая берет на вход рецензию на фильм и прогнозирует, является ли она положительной или нет. Итак, дана рецензия на фильм…

…мы хотим, чтобы наша нейронная сеть предсказала, что она положительная.
Это может показаться простой задачей классификации, но стандартные нейронные сети сталкиваются здесь с двумя серьезными проблемами.
Во‑первых, мы имеем дело с переменной длиной входных данных. Стандартная нейронная сеть с трудом справляется с обработкой входных данных разной длины. Например, если мы обучаем нашу нейронную сеть, используя рецензию на фильм из трех слов, то размер входных данных будет фиксированным — ровно три слова. Но что, если мы захотим скормить ей рецензию подлиннее?

Она не сможет обработать приведенную выше рецензию, потому что она состоит из двенадцати слов. В отличие от предыдущих статей, где у нас было фиксированное количество входных данных (в модели для определения выручки от продажи мороженого было два входа — температура и день недели), в данном случае модель должна быть гибкой и адаптироваться к любому количеству слов, которые ей придется обрабатывать.
Во‑вторых, наши входы последовательные. Обычная нейронная сеть не понимает направленность входов, а это очень важно. В двух предложениях могут быть одни и те же слова, но в разном порядке, из‑за чего они могут передавать совершенно противоположные смыслы.

Учитывая эти проблемы, нам нужен метод последовательной обработки динамического числа входов. Именно здесь RNN и раскрывает свой потенциал.
Мы подходим к этой задаче так: сначала обрабатываем первое слово рецензии — «that»:

Затем используйте эту информацию для обработки второго слова, «was»:

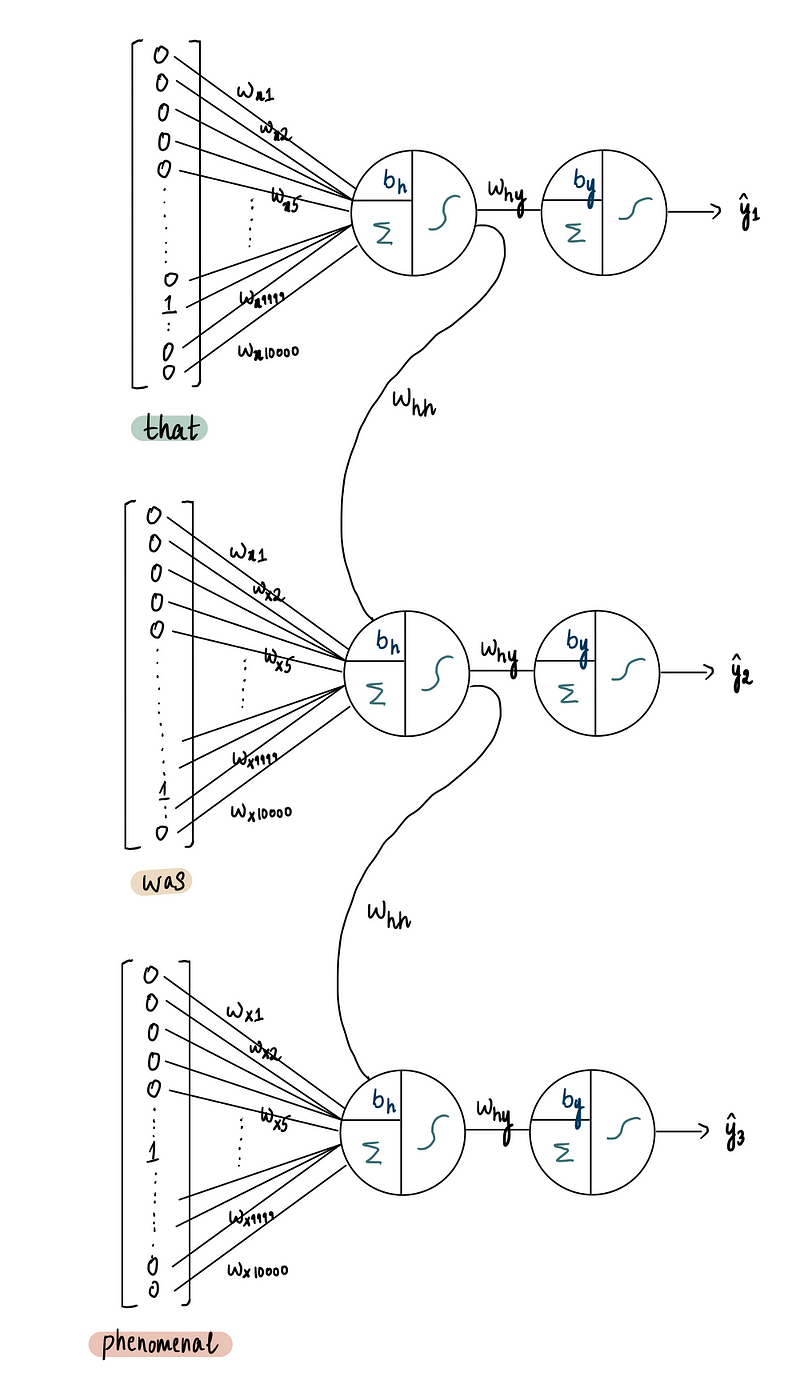
И наконец, используем всю вышеперечисленную информацию для обработки последнего слова, «phenomenal», на основе чего делаем прогноз относительно тональности рецензии:

Прежде чем мы начнем строить нашу нейронную сеть, нам нужно обсудить наши входы. Входы для нейронной сети должны быть числовыми. Однако в данном случае мы используем слова, поэтому нам нужно преобразовать эти слова в числа. Существует несколько способов сделать это, но сегодня мы будем использовать наиболее примитивный метод.
В следующих статьях мы рассмотрим более сложные методы решения этой задачи.
Представим, что у нас есть большой словарь из 10 000 слов. Мы (наивно) предположим, что все слова, встречающиеся в рецензиях, можно найти в этом словаре. Каждое слово сопоставляется с соответствующим числом.

Чтобы преобразовать слово «that» в ряд чисел, нужно просто определить, с каким числом сопоставлено «that»…

…а затем представить его в виде вектора из 10 000 нулей, за исключением 8600-го элемента, который будет единицей:
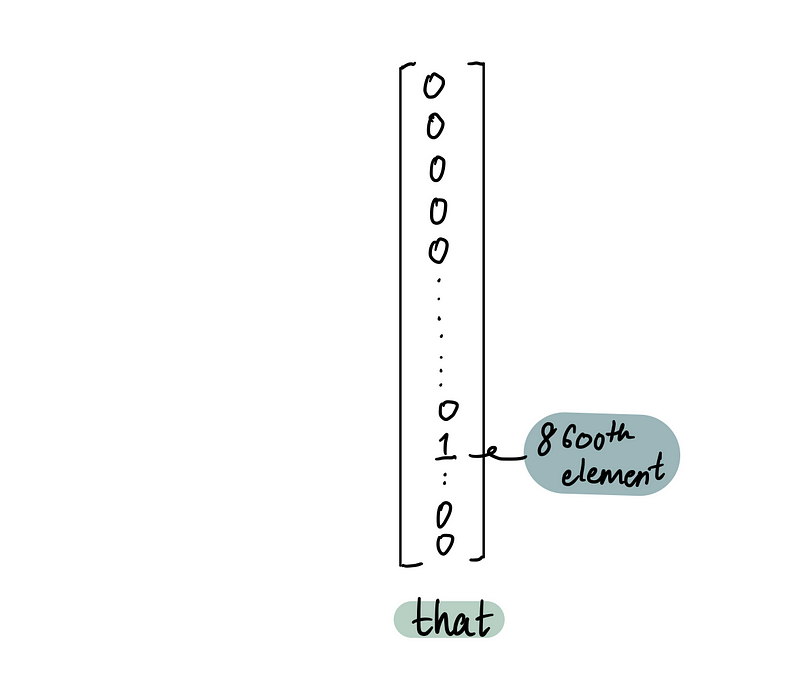
Аналогично, числовые представления для следующих двух слов, «was» (9680-е слово в словаре) и «phenomenal» (4242-е слово в словаре), будут:

Вот так мы берем слово и преобразуем его в понятный для нейронной сети вход.
Теперь перейдем к проектированию самой нейронной сети. Для простоты предположим, что наша сеть имеет 10 000 входов (= 1 слово), один скрытый слой, состоящий из одного нейрона, и один выходной нейрон.

И конечно, если это полностью обученная нейронная сеть, то каждый вход будет иметь соответствующие веса, а нейроны будут иметь смещения.
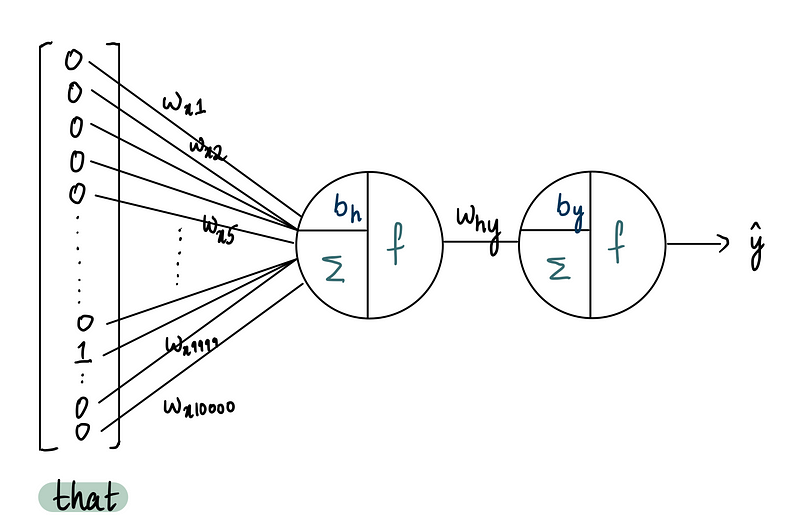
В этой сети входные веса обозначены как wᵢ, где i указывает вход. Смещения (bias term) в нейроне скрытого слоя обозначены bₕ. Вес, соединяющий скрытый слой с выходным нейроном — wₕᵧ. Наконец, смещение в выходном нейроне представлено bᵧ, а y обозначает наш выход.
В качестве функции активации скрытого нейрона мы будем использовать функцию гиперболического тангенса (tanh).

Мы уже обсуждали ее в первой статье, но в качестве напоминания — tanh принимает входные данные и выдает на выход значение в диапазоне от -1 до 1. Большие положительные значения стремятся к 1, а большие отрицательные значения приближаются к -1.

Чтобы определить тональность текста, мы можем использовать сигмоидальную функцию активации в выходном нейроне. Эта функция берет выход скрытого слоя и выдает значение между 0 и 1, представляющее собой вероятность позитивного настроения. Прогноз, близкий к 1, указывает на положительный отзыв, в то время как прогноз, близкий к 0, говорит о том, что он вряд ли будет положительным.

Этот метод определенно работает, но есть более сложный подход, который может дать лучшие результаты! Если вы дочитаете статью до конца, то увидите новую, мощную и повсеместно распространенную функцию активации (Softmax), которая лучше решает эту задачу.
С этими функциями активации наша нейронная сеть выглядит следующим образом:

Эта нейронная сеть получает текстовый вход и прогнозирует вероятность того, что он будет иметь позитивную тональность. В приведенном выше примере сеть обрабатывает слово «that» и прогнозирует вероятность его позитивной тональности. Разумеется, само по себе слово «that» не дает никаких особых подсказок о настроении. Теперь нам нужно понять, как включить в сеть следующее слово. Вот тут‑то и вступает в игру рекуррентный аспект RNN, который требует от нас изменить базовую структуру.
Мы вводим второе слово рецензии, «was», создавая точную копию вышеприведенной нейронной сети. Однако вместо «that» в качестве входного сигнала мы используем «was»:

Точная копия нейронной сети со входом «was»
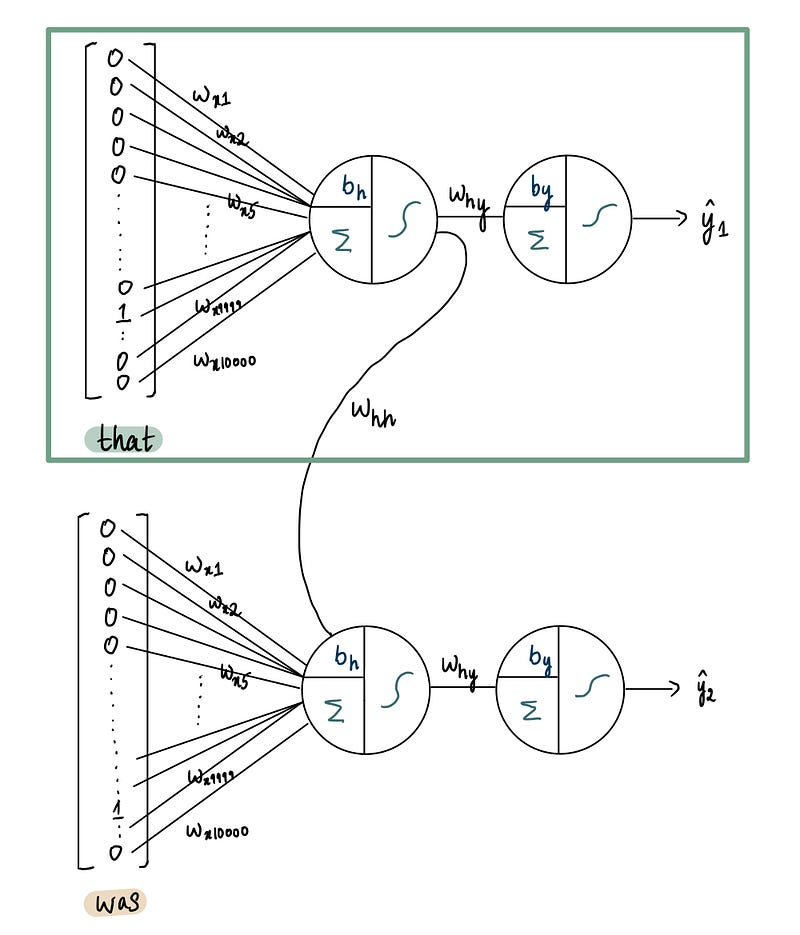
Помните, что в этой нейронной сети мы также хотим использовать информацию, полученную от предыдущего слова «this». Поэтому мы берем выход из скрытого слоя предыдущей нейронной сети и передаем его в скрытый слой текущей сети:

Включение данных из предыдущей нейронной сети с входом «that» в текущую с входом «was»
Это очень важный шаг, поэтому давайте разберем его по порядку.
Из первой статьи мы узнали, что обработка информации каждым нейроном состоит из двух этапов: сумматора и функции активации (пожалуйста, прочитайте первую статью, если не знакомы с этими терминами). Давайте посмотрим, как это выглядит в нашей первой нейронной сети.
В нейроне скрытого слоя первой нейронной сети первым шагом является суммация:

Нейронная сеть 1 — скрытый нейрон — часть 1 суммация
Здесь мы умножаем каждый из входов на соответствующие веса и добавляем смещения к сумме всех произведений:

Чтобы упростить это уравнение, давайте представим его таким образом, где wₓ — это входные веса, а x — входные данные:

Нейронная сеть 1 — скрытый нейрон — часть 1 суммация
Далее, на шаге 2, мы пропускаем эту сумму через функцию активации, tanh:


Нейронная сеть 1 — скрытый нейрон — часть 2 функция активации = h1
В результате мы получаем выход h₁ из скрытого слоя первой нейронной сети. Отсюда у нас есть два варианта — передать h1 выходному нейрону или передать его в скрытый слой следующей нейронной сети.
(вариант 1) Если мы хотим получить прогноз тональности только для «that», то мы можем взять h₁ и передать его выходному нейрону:

Вариант 1 — передать h1 выходному нейрону в первой нейронной сети
Для выходного нейрона мы выполняем шаг суммации…


Нейронная сеть 1 — выходной нейрон — часть 1 суммация
…а затем применяем сигмоидальную функцию к этой сумме…

Нейронная сеть 1 — выходной нейрон — часть 2 активация = ŷ1
… что дает нам прогноз позитивной тональности:

Нейронная сеть 1 — выходной нейрон — часть 2 активация = ŷ1
Таким образом, это ŷ₁ дает нам предсказанную вероятность того, что «that» имеет позитивную тональность.
(вариант 2) Но это не то, что нам нужно. Поэтому вместо того, чтобы передавать h₁ выходному нейрону, мы передаем эту информацию следующей нейронной сети:

Вариант 2 — передать h1 скрытому нейрону во второй нейронной сети
Подобно другим частям нейронной сети, где у нас есть входные веса, у нас также есть входной вес, wₕₕ, для входа от одного скрытого слоя к другому. Скрытый слой учитывает h₁, добавляя произведение h₁ и wₕₕ к шагу суммации в скрытом нейроне. Таким образом, обновленный шаг суммации в скрытом нейроне второй нейронной сети будет таким:


Нейронная сеть 2 — скрытый нейрон — часть 1 суммация
Важно отметить, что все смещения и веса в сети остаются неизменными, поскольку они просто копируются из предыдущей сети.
Затем эта сумма проходит через функцию tanh…

Нейронная сеть 2 — скрытый нейрон — часть 2 функция активации
…получая в итоге h₂ — выход скрытого слоя во второй нейронной сети:

Нейронная сеть 2 — скрытый нейрон — часть 2 функция активации
Отсюда мы снова можем получить прогноз тональности, пропустив h₂ через выходной нейрон:


Нейронная сеть 2 — выходной нейрон — часть 1 и 2 = ŷ2
Здесь ŷ₂ — это спрогнозированная вероятность того, что «that was» имеет позитивную тональность.
Но мы знаем, что это еще не конец ревью. Поэтому мы повторим этот процесс, снова клонируя эту сеть, но уже с входом «phenomenal», и передадим выход предыдущего скрытого слоя в текущий скрытый слой.

В результате обработки в нейроне скрытого слоя…

Нейронная сеть 3— скрытый нейрон — часть 1 и 2 = h3
…полученный выход, h₃:

Нейронная сеть 3 — скрытый нейрон — часть 1 и 2 = h3
Поскольку это последнее слово в рецензии и, следовательно, последний вход, мы передаем эти данные внешнему нейрону…

Нейронная сеть 3 — выходной нейрон — часть 1 и 2 = ŷ3
…чтобы получить окончательный прогноз тональности:

Нейронная сеть 3 — выходной нейрон — часть 1 и 2 = ŷ3
ŷ₃ является тональностью рецензии на фильм, которую мы хотим определить, и это то, как мы достигаем того, что мы нарисовали в начале!

Формальное представление
Если мы дополним приведенную выше схему деталями, то получим примерно следующее:

На каждом этапе процесса вход x проходит через скрытый слой и генерирует выход h. Этот выход либо переходит в скрытый слой следующей нейронной сети, либо приводит к прогнозированию тональности, изображенному как ŷ. Каждый этап включает в себя весовые коэффициенты и коэффициенты смещения (смещение не показано на диаграмме). Важно подчеркнуть, что мы объединяем все скрытые слои в один компактный прямоугольник. Хотя наша модель содержит только один слой с одним нейроном в скрытом слое, более сложные модели могут включать несколько скрытых слоев с множеством нейронов, все из которых сведены в этот прямоугольник, называемый скрытым состоянием. В этом скрытом состоянии заключена абстрактная концепция скрытого слоя.
По сути, это упрощенная версия данной нейронной сети:
Стоит также отметить, что для простоты мы можем представить все это в виде этой упрощенной диаграммы:

Суть этого процесса заключается в рекуррентной подаче выходных данных из скрытого слоя обратно в себя же, поэтому нейронную сеть называют рекуррентной. Именно так эти нейронные сети часто изображаются в учебниках.
С математической точки зрения мы можем свести все к двум фундаментальным уравнениям:

Весь процесс представлен двумя формулами
Первое уравнение включает в себя полное линейное преобразование, которое происходит в скрытом состоянии. В нашем случае это преобразование — функция активации tanh в отдельном нейроне. Второе уравнение обозначает преобразование, происходящее в выходном слое, которое в нашем примере представляет собой сигмоидальную функцию активации.

Весь процесс представлен двумя формулами
Какие задачи решает RNN?
Многие-к-одному
Мы только что обсудили сценарий, в котором множество входных данных (в нашем случае все слова в рецензии) подаются в RNN. Затем RNN генерирует один выход, представляющий тональность рецензии. Хотя можно иметь выход на каждом шаге, для нас интерес представляет конечный выход, поскольку в нем заключена тональность всей рецензии.

Еще один пример — завершение текста (text completion). Когда мы хотим, чтобы RNN предсказывала следующее слово, на основе данной строки слов.

Один-к-многим

Классическим примером задачи «один‑к-многим» является генерация описания изображения. Здесь на вход подается изображение, а на выходе получается надпись, состоящая из нескольких слов.
Многие-к-многим

Этот тип RNN используется для таких задач, как машинный перевод, например, перевод английского предложения на русский.
Недостатки
Теперь, когда мы разобрались с тем, как работает RNN, стоит рассмотреть, почему они не так широко используются (а вот и неожиданный поворот!). Несмотря на свой потенциал, RNN сталкиваются с серьезными проблемами в процессе обучения, в частности из‑за так называемой проблемы исчезающего градиента. Эта проблема имеет тенденцию усиливаться по мере разворачивания RNN, что, в свою очередь, усложняет процесс обучения.
В идеальном сценарии мы хотим, чтобы RNN в равной степени учитывал как входные данные текущего шага, так и предыдущих шагов:

Однако на самом деле это выглядит примерно так:

Каждый шаг немного забывает предыдущий, что приводит к проблеме кратковременной памяти, известной как проблема исчезающего градиента. По мере того как RNN обрабатывает все больше шагов, она начинает испытывать трудности с сохранением информации, полученной на предыдущих шагах.
При наличии всего трех входов эта проблема не слишком заметна. Но что, если у нас шесть входов?

Мы видим, что информация из первых двух шагов практически отсутствует в последнем шаге, что является существенной проблемой.
Вот пример, иллюстрирующий этот момент, на примере задачи завершения текста. Если вам нужно закончить это предложение, то RNN может с этим справиться.

Однако если добавить больше слов, RNN будет сложнее точно предсказать следующее слово. Это происходит потому, что RNN может забыть контекст, заданный начальными словами, из‑за увеличения расстояния между ними и словом, которое нужно предсказать.

Это подчеркивает тот факт, что хотя RNN отлично звучат в теории, на практике они часто оказываются неэффективными. Чтобы решить проблемы с кратковременной памятью, мы используем специализированные типы нейронных сетей, известные как сети с долговременной памятью (Long Short‑Term Memory — LSTM). Но об этом мы расскажем в следующей части. Так что следите за новостями!
Бонус: функция активации Softmax
Ранее мы говорили об альтернативном, гораздо более эффективном способе прогнозирования тональности. Давайте сделаем несколько шагов назад к чертежной доске и вернемся к тому моменту, когда мы выбирали функцию активации для нашего выходного нейрона.

Но в этот раз мы сосредоточимся на другом. Давайте рассмотрим базовую нейронную сеть, отбросив рекуррентные аспекты. Какова наша цель? Спрогнозировать тональность одного входного слова, а не всей рецензии на фильм.
Ранее наша модель была нацелена на вывод вероятности того, что входные данные являются позитивными. Для этого мы использовали сигмоидальную функцию активации в выходном нейроне, которая выдает значения вероятности. Например, если мы вводим слово «terrible», наша модель в идеале должна выдать низкое значение, указывающее на низкую вероятность позитивной тональности.

Однако, если подумать, это не такой уж и хороший результат. Низкая вероятность позитивной тональности не обязательно означает негатив — она также может означать, что входные данные были нейтральными. Так как же нам улучшить этот результат?
Подумайте вот о чем: Что если мы хотим узнать, была ли рецензия на фильм положительной, нейтральной или отрицательной?
Таким образом, вместо одного выходного нейрона, который выдает прогноз вероятности того, что вход будет позитивным, мы можем использовать три выходных нейрона. Каждый из них будет прогнозировать вероятность того, что отзыв будет положительным, нейтральным и отрицательным, соответственно.

Точно так же, как мы использовали сигмоидальную функцию для сети нейронов с одним выходом для вывода вероятности, мы можем применить тот же принцип к каждому из этих нейронов в нашей текущей сети и использовать сигмоидальную функцию для всех них.

И каждый нейрон будет выдавать соответствующее значение вероятности:

Однако есть одна проблема: вероятности не складываются как нужно (0.1 + 0.2 + 0.85!= 1), так что это не самый лучший обходной путь. Простое натягивание сигмоидальной функции на все выходные нейроны не решает проблему. Нам нужно найти способ нормализовать эти вероятности по трем выходам.
Здесь мы вводим в наш арсенал мощную функцию активации — softmax (многопеременная логистическая функция). При использовании функции активации softmax наша нейронная сеть приобретает новую форму:

Хотя поначалу это может немного напугать, на самом деле функция softmax довольно проста. Она просто берет выходные значения (ŷ) от наших выходных нейронов и нормализует их.
Однако важно отметить, что для этих трех выходных нейронов мы не будем использовать никакую функцию активации. Выходы (ŷ) будут результатом, который мы получим непосредственно после шага суммации.
Если вам нужно освежить в памяти, что такое шаг суммации и шаг активации в нейроне, то в этой статье мы подробно рассматривали внутреннее устройство нейрона!
Мы нормализуем эти результаты ŷ с помощью формулы softmax. Эта формула дает прогноз вероятности позитивной тональности:

Аналогичным образом мы можем получить вероятности прогноза негативных и нейтральных исходов:


Давайте посмотрим на это в действии. Например, если в качестве входных данных мы используем слово «terrible», то вот какие значения будут получены в результирующем ŷ:

Затем мы можем взять эти значения и подставить их в формулу softmax, чтобы вычислить вероятность того, что слово «terrible» имеет положительную коннотацию.

Это означает, что при использовании комбинированных выходов нейронов вероятность того, что слово «terrible» имеет позитивную тональность, составляет 0.05.
Если мы хотим рассчитать вероятность того, что вводимое слово будет нейтральным, мы используем аналогичную формулу, только изменим числитель. Таким образом, вероятность того, что слово «terrible» будет нейтрально, составляет:

А вероятность того, что «terrible» будет отрицательным, является:

И вуаля! Теперь вероятности складываются в 1, что делает нашу модель более объяснимой и логичной.
Итак, когда мы спрашиваем нейронную сеть: «Какова вероятность того, что слово «terrible» имеет негативную тональность?», мы получаем довольно простой ответ. Нейросеть уверенно заявляет, что вероятность того, что слово «terrible» имеет негативную коннотацию, составляет 85%. И в этом вся прелесть функции активации Softmax!
На сегодня на этом все! Мы рассмотрели две важные темы — рекуррентные нейронные сети и функцию активации Softmax. Это строительные блоки для многих продвинутых концепций, в которые мы погрузимся позже.
Примечание: Все иллюстрации принадлежат автору, если не указано иное
В завершение приглашаем всех желающих на открытые уроки по машинному обучению:
5 марта. Кластеризация временных рядов (ищем связанные котировки акций). Узнать подробнее
19 марта. Recommend or not recommend? Классические алгоритмы рекомендательных систем. Узнать подробнее
