[Перевод] Что общего у собеседования кодера и игры «Змейка»?

Если вы родились в 80-х или 90-х, то наверняка слышали о Snake. То есть, скорее всего, вы потратили безумное количество времени на своём Nokia 3310, выращивая огромную змею на мелком экранчике. Что ещё мы помним о телефонах Nokia?
Их неразряжающийся аккумулятор, правда? Как такой «примитивный» телефон выдерживал долгие часы игры в «Змейку» без разрядки аккумулятора?
Короткий (и неполный) ответ: всё дело в методе скользящего окна.
Мы бы с радостью написали целую статью о Snake, но в этом посте мы всё-таки рассмотрим менее зрелищный, но тем не менее очень важный метод, и ответим на вопросы типа:
- Почему мы и другие программисты считаем его фундаментальным алгоритмом?
- Почему он так часто используется на технических собеседованиях?
- Как он использовался в Snake и других «реальных» областях применения?
- На какие самые популярные вопросы собеседований можно (лучше) ответить с помощью метода скользящего окна?
Если вы готовитесь к собеседованию, читаете статью из интереса, или хотите узнать что-то новое, то продолжайте читать. При этом вы можете спокойно пропускать лишнее и переходить к самым интересным разделам.
NB: Если вас волнует только «Змейка» (и мы вас вполне понимаем), то можете перейти к самому концу поста.
Давайте приступим.
Несмотря на сложности алгоритмического программирования, существует достаточно короткий список принципов, необходимых для решения задач. Одним из таких принципов является метод скользящего окна.

Рисунок 1. Скользящее окно
Оконная парадигма
Метод скользящего окна возник из более общего принципа кадрирования.
Кадрирование заключается в получении состояния системы и ограничении области обзора только его частью, называемой «окном». Это создаёт разделение между алгоритмом кадрирования и алгоритмом, применяемым к тем элементам, которые видимы через окно, что упрощает оба алгоритма.
Особый случай — это состояние, состоящее из последовательности объектов, например, из массива или строки. Если задать окно, то мы увидим подпоследовательность. Теперь мы можем применить любую обработку к этому ограниченному интервалу, как будто в последовательности больше нет никаких значений. Благодаря ограничению интервала мы делаем всю задачу меньше. Теперь рассмотрим свойство скольжения: переместим окно на одну позицию вправо, и получим другую подпоследовательность, к которой тоже можно применить обработку.
И здесь начинается наше приключение. Если применять алгоритм к каждому окну по отдельности, то в результате у нас получится тактика грубого перебора.
Однако красота метода скользящего окна заключается в том, что она позволяет изменить структуру алгоритма таким образом, чтобы он использовал преимущества самого процесса смещения окна. И целью всего этого является создание более хороших и быстрых алгоритмов.
Мы можем повысить скорость выполнения практически любого алгоритма, применённого к скользящему окну, по крайней мере, теоретически. При сдвиге окна меняются только два элемента. Самый старый выбывает, и в кадр попадает самый новый.

Рисунок 2. Сдвиг элементов (красный: выбыл, зелёный: прибыл)
Если грубому перебору требуется k шагов для обработки одного окна длиной k, и в последовательности есть n окон, то для выполнения работы алгоритму грубого перебора потребуется n·k шагов. Но поскольку при каждом шаге меняется всего два элемента, мы можем достичь общего времени выполнения, приблизительно пропорционального 2n.
Если мы говорим, что простое прохождение по последовательности занимает время O(n), то это значит, что на общей последовательности никакой алгоритм не может быть быстрее, чем O(n). Этот анализ показал нам, что правильное применение метода скользящего окна может привести к изобретению алгоритмов обработки полных последовательностей, способных выполняться за время O(n).
Другими словами, он обещает нам, что мы можем изобрести идеальные для решения задачи алгоритмы, быстрее которых не может быть!
Закончив с необходимым введением, мы рассмотрим три задачи программирования, которые можно решить с помощью этой общей концепции алгоритмов, и покажем конкретные примеры того, как они использовались в реальных случаях.
Задача программирования 1: скользящее среднее
Задача, которую нужно решить: создать алгоритм, вычисляющий скользящее среднее числового ряда.
Для заданного ряда a0, a1, … an-1 и параметра k, 0 < k <= n мы должны сгенерировать новую последовательность, такую, чтобы каждый элемент являлся средним значением k последовательных элементов исходной последовательности:

Рисунок 3. Eq Average
Контекст: скользящее среднее полезно для сглаживания потока входных данных. Если на числа влияет шум, то сырые данные будет сложно отображать. Как видно из двух иллюстраций ниже, сглаживание позволяет получить более информативную схему.

Рисунок 4. Скользящее среднее сглаживает входные данные
Эту задачу можно эффективно решить с помощью метода скользящего окна. Он сразу же раскрывает общую черту большинства таких алгоритмов: первые k-1 элементов не создают выходных данных. Только при заполнении всего окна мы можем получить первую порцию результатов. Все последующие окна создают по одному результату каждое. Поэтому последовательность из n элементов при использовании алгоритма скользящего окна создаёт последовательность из n-k+1 результатов.
А теперь перейдём к реализации. Среднее значение окна — это сумма всех элементов, поделённая на длину окна.

Рисунок 5. Eq Sum
При такой формулировке мы сразу же можем увидеть преимущество использования метода скользящего окна. Сумму значений окна можно вычислить из суммы значений предшествующего ему окна:

Рисунок 6. Eq Optimization
Вычисление суммы первого окна займёт k шагов, а для каждого следующего окна потребуется всего две дополнительные операции.
Ниже показана реализация этого ответа на C++, передающая первые k элементов для создания первых выходных данных. Все другие выходные числа вычисляются с помощью оптимизированной формулы суммирования.
double* moving_average(double* data, int n, int k)
{
assert(data != NULL);
assert(n > 0);
assert(0 < k && k <= n);
double* result = new double[n — k + 1];
double sum = 0;
for (int i = 0; i < k; i++)
{
sum += data[i];
}
result[0] = sum / k;
for (int i = k; i < n; i++)
{
sum = sum — data[i — k] + data[i];
result[i — k + 1] = sum / k;
}
return result;
}
Основной смысл этого алгоритма в том, что каждый элемент в исходной последовательности обрабатывается максимум дважды, что создаёт общую временную сложность O(n).
Задача программирования 2: подпоследовательность с максимальной суммой
Задача, которую нужно решить: создать алгоритм нахождения подпоследовательности с наибольшей суммой из всех возможных подпоследовательностей.
Это может стать настоящей проблемой, если входные данные содержат отрицательные значения.
И здесь снова можно использовать метод скользящего окна, для создания решения со временем выполнения O(n). Только на этот раз длина окна не будет постоянной. На самом деле, поскольку сама задача заключается в нахождении самого подходящего окна, длина окна может в процессе меняться.
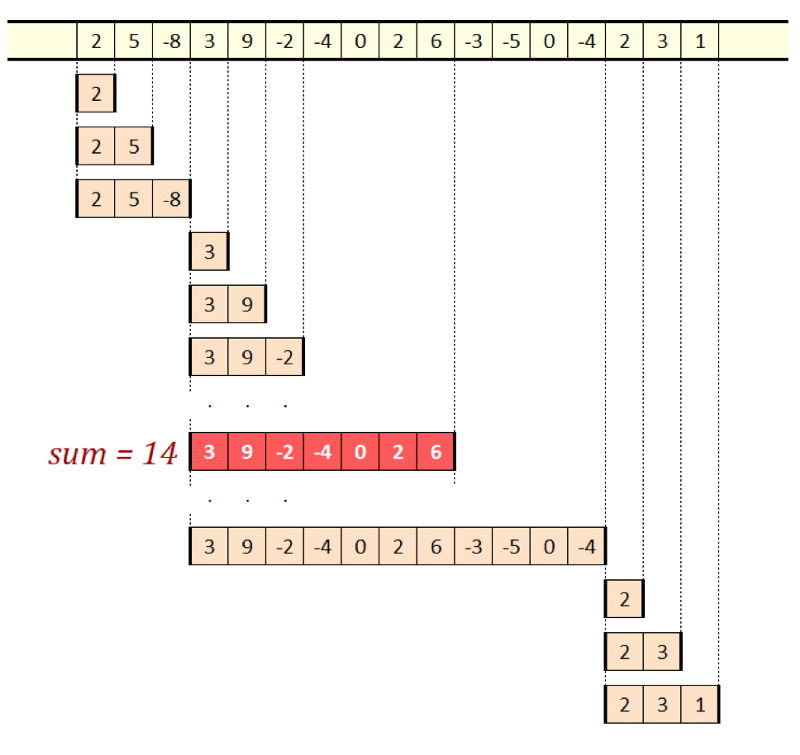
Рисунок 7. Максимальная сумма, решение со скользящими окнами
Идея заключается в том, чтобы наблюдать за происходящим, когда у нас уже есть окно с определённой суммой. Затем мы хотим добавить следующее значение. Это значение может быть прибавлено к сумме окна. Но оно может быть взято и как совершенно новое окно единичной длины. Зададим вопрос: какое из них будет иметь бОльшую сумму? Каким бы оно ни было, мы сохраним его как новое окно и переместимся к следующему входному значению, повторив ту же процедуру. Посмотрите на рисунок выше, на котором показано, как окна постепенно скользят вдоль последовательности.
Выигрышным вариантом всегда будет подпоследовательность с максимальной суммой, заканчивающаяся на текущем входном элементе. Каждое окно отбрасывается сразу же, когда её сумма становится отрицательной: это ситуация, при которой число в одиночку лучше, чем в сочетании с максимальным предшествующим ему окном.
Нам остался единственный последний шаг — определение общего максимума. Кандидатами являются все окна, потому что они скользят по направлению к концу последовательности. После завершения последовательности окно с наибольшей суммой будет являться подпоследовательностью с максимальной суммой.
Ниже представлена прямолинейная реализация алгоритма на C++. И снова, каждый элемент последовательности рассматривается не более двух раз, что составляет общую временную сложность функции O(n).
std::tuple max_sum_subsequence(int* data, int n)
{
assert(data != NULL);
assert(n > 0);
int bestStart = 0;
int bestLength = 1;
int maxSum = data[0];
int curStart = bestStart;
int curLength = bestLength;
int curSum = maxSum;
for (int i = 1; i < n; i++)
{
if (curSum < 0)
{
curStart = i;
curLength = 1;
curSum = data[i];
}
else
{
curLength += 1;
curSum += data[i];
}
if (curSum > maxSum)
{
bestStart = curStart;
bestLength = curLength;
maxSum = curSum;
}
}
return std::tuple(bestStart, bestLength, maxSum);
} Задача программирования 3: максимумы всех k-подпоследовательностей
Задача, которую нужно решить: создать алгоритм, вычисляющий максимумы всех подпоследовательностей длины k в числовой последовательности длины n. Примечание: это сложная задача.
Этот алгоритм применяется в обработке изображений, где, как можно догадаться, алгоритмы со временем выполнения O(n) ценятся больше всех остальных.

Рисунок 8. Максимумы
При скольжении окна оно создаёт на выходе максимальное содержащееся значение. Сложная часть решения заключается в том, что нет формулы, дающей максимум заданного окна. Мы можем взять в качестве результата один из элементов.
Но нельзя сказать, что мы не можем выиграть от использования метода скользящего окна. Вот в чём заключается идея: предположим, у нас есть окно с четырьмя значениями, как показано на рисунке выше.
Когда в кадр попадает дополнительное значение, нам нужно понять, как оно соотносится с уже имеющимися значениями. Начнём с того, что при продолжении скольжения окна все предыдущие значения выпадают из него прежде, чем выпадет это новое значение. Это важное заключение. Если предыдущее значение меньше нового, то оно никогда не станет максимумом, просто потому, что новое, более крупное значение всегда будет затмевать его.

Рисунок 9 . Скольжение максимума
Это приводит нас к идее о том, чтобы не признавать каждое новое значение и удалять все меньшие значения, которые оно находит в окне при скольжении окна, как показано на рисунке ниже. Эта операция имеет другое последствие.
Если каждое добавленное справа значение удаляет все меньшие значения, то окно будет содержать только неувеличивающуюся, прерывистую подпоследовательность исходного окна. Ещё одно последствие заключается в том, что теперь становится очевидным — самый левый элемент окна является максимальным значением, которое мы должны вычислить.
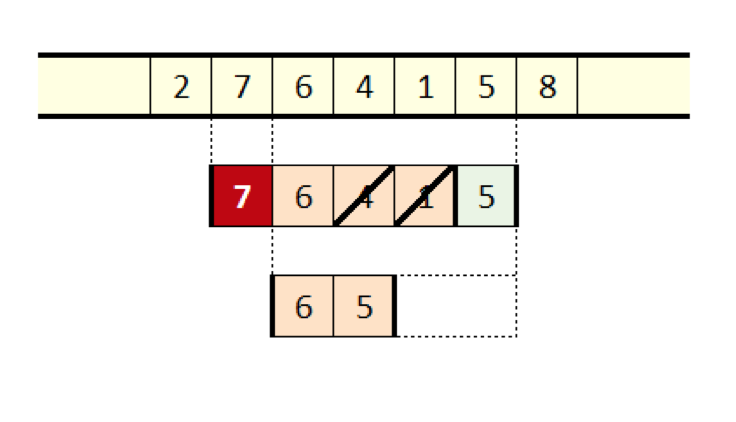
Рисунок 10. Отсеивание максимумом
Нужно уточнить ещё одну деталь. При скольжении окна самое левое значение последовательности выпадает. Это значение уже могло быть удалено более крупным значением. Или же оно могло пережить все следующие за ним значения справа. В последнем случае значение из входных данных будет самым левым значением в кадре, и теперь настало время удалить его.
На рисунке ниже показан весь процесс, применённый к последовательности из семи элементов с длиной окна, равным четырём.
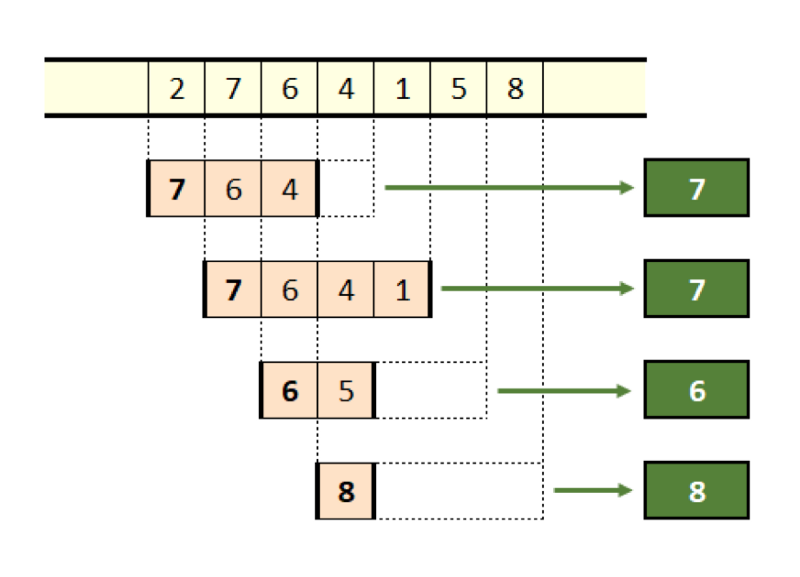
Рисунок 11. Максимумы всего
На этом мы завершим описание алгоритма и начнём его реализацию. Обычная реализация основана на двухсторонней очереди (dequeue). Dequeue поддерживает добавление в очередь и удаление из неё с обоих концов, и именно эти операции мы используем для реализации алгоритма.
void insert_maximum_candidate(int value, bounded_deque &maximums)
{
while (!maximums.empty() && maximums.back() < value)
maximums.pop_back();
maximums.push_back(value);
}
void remove_maximum_candidate(int value, bounded_deque &maximums)
{
if (!maximums.empty() && maximums.front() == value)
maximums.pop_front();
}
int* range_maximums(int* data, int n, int k)
{
assert(data != NULL);
assert(n > 0);
assert(0 < k && k <= n);
bounded_deque maximums(k);
for (int i = 0; i < k — 1; i++)
insert_maximum_candidate(data[i], maximums);
int* result = new int[n — k + 1];
for (int i = k — 1; i < n; i++)
{
insert_maximum_candidate(data[i], maximums);
result[i — k + 1] = maximums.front();
remove_maximum_candidate(data[i — k + 1], maximums);
}
return result;
}
В этом решении мы используем собственную реализацию Dequeue под названием fixed_deque. В отличие от std::deque, этот класс поддерживает буфер для данных фиксированной длины, который ускоряет выполнение по крайней мере на один порядок. Внутри он работает как кольцевой буфер, который чрезвычайно эффективен. Как бы то ни было, класс fixed_deque имеет тот же публичный интерфейс, что и std::deque (единственная разница заключается в том, что его конструктор ожидает размер буфера) и при желании вы можете заменить его на std::deque. Кроме значительного снижения скорости выполнения, не будет никаких других последствий.
Как и в предыдущих примерах, мы можем проанализировать временную сложность этой реализации. Каждое значение из входной последовательности не более одного раза подвергается помещению в очередь и удалению из неё. То есть на одно входное число выполняется максимум две операции, и общая временная сложность алгоритма равняется O(n). Также этому алгоритму требуется дополнительное пространство O(k), где k — длина окна. (Стоит заметить, что предыдущим алгоритмам требовалось только O(1) пространства.)
Думать нестандартно
Мы рассмотрели три алгоритма, основанных на методе скользящего окна. Как мы и обещали, каждый из них выполняется за время O(n). Также я хотел бы показать вам, как тот же метод применяется в двух совершенно различных областях.
Во-первых, в протоколах маршрутизации пакетов, например в TCP/IP, скользящее окно используется для согласования Internet Protocol (IP) с Transmission Control Protocol (TCP). IP никогда не может гарантировать, что пакеты будут получены в том же порядке, в котором отправлялись. В то же время, TCP как раз обеспечивает эту гарантию. Здесь скользящее окно становится одним из самых важных составляющих успеха связки протоколов TCP/IP.
TCP-получатель поддерживает окно ожидаемых им пакетов. Пакеты поступают по менее совершенному (но более реалистичному) IP, и могут прийти не в нужном для заполнения соответствующих позиций окна порядке. Однако как только прибывает самый левый пакет, окно TCP сдвигается как можно правее, подтверждает отправителю получение всех смежных пакетов и передаёт их на выход. Это, в свою очередь, сигнализирует отправителю о возможности начала передачи последующих пакетов в сеть IP.
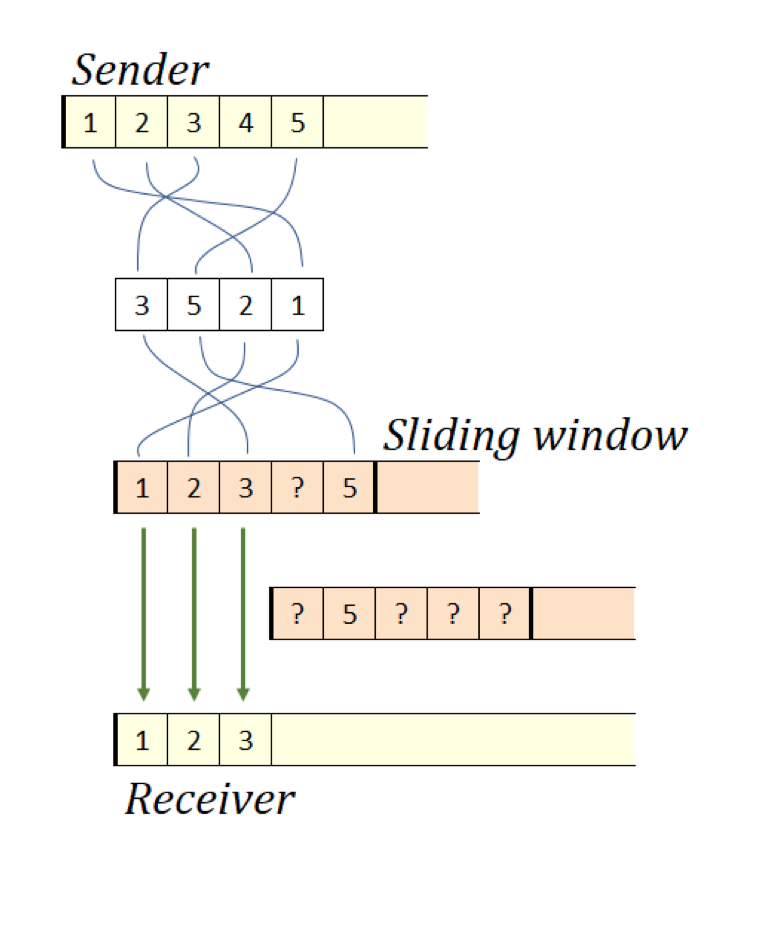
Рисунок 12. TCP-IP
Вы уже догадались, чему будет посвящён второй (и последний) пример.
Разумеется, «Змейке». Когда эта игра появилась несколько десятилетий назад, большинство знало её по сотовым телефонам Nokia.

Рисунок 13. Snake
Догадываетесь? Змейка сама является скользящим окном! Когда змея движется, нам достаточно отрисовывать на экране всего два блока — хвост становится блоком-фоном, а бывший фон перед головой змеи становится новой головой.

Рисунок 14. «Змейка» = скользящее окно
Результатом применения метода скользящего окна стало то, что каждый кадр игры стоит нам отрисовки максимум двух примитивных блоков, вне зависимости от длины змеи. Это позволяло реализовывать игру на примитивном «железе» без лишнего расхода заряда аккумулятора.
Подводим итог
В этой статье мы проанализировали общий алгоритм, называемый скользящим окном. Вы узнали, что эту технику можно применить для оптимизации алгоритмов обработки последовательностей данных. При удачном применении техника обеспечивает создание алгоритмов, выполняемых за время O(n) для последовательности из n объектов, что является самой оптимальной конструкцией алгоритмов.
В качестве конкретных примеров решения задач мы разработали три отличающихся алгоритма, работающих с числовыми последовательностями. Все эти алгоритмы применяются в реальном мире для обработки общих данных и обработки изображений. Это объясняет, почему метод скользящего окна дожил до наших дней и остаётся полезным инструментом в создании алгоритмов. Поэтому вы, вероятнее всего, услышите о нём на технических собеседованиях.
