[Перевод] Баг с псионическими сигнатурами в Java
В классическом научно-фантастическом сериале BBC Доктор Кто часто используется следующий сюжетный приём: Доктору удаётся избежать неприятностей, показав удостоверение личности, которое на самом деле совершенно пустое. Разумеется, удостоверение сделано из специальной «психобумаги», заставляющей смотрящего на неё человека видеть то, что захочет Доктор: пропуск, ордер или что-то ещё.

Оказывается, некоторые новые релизы Java тоже были подвержены подобному трюку в реализации широко используемых сигнатур ECDSA. Если запустить одну из уязвимых версий, то нападающий легко сможет подделать некоторые типы сертификатов SSL и handshake (что позволяет вмешиваться в обмен данными и модифицировать их), подписанные JWT, декларации SAML или id-токены OIDC и даже сообщения аутентификации WebAuthn. И для всего этого достаточно цифрового аналога чистого листа бумаги.
Опасность этого бага сложно преувеличить. Если вы используете сигнатуры ECDSA для любых перечисленных механизмов защиты, то нападающий может тривиальным образом полностью обойти их, если на вашем сервере запущена какая-то из версий Java 15, 16, 17, или 18 до Critical Patch Update (CPU) за апрель 2022. Для понимания контекста скажу, что почти все устройства WebAuthn/FIDO в реальном мире (в том числе Yubikey) используют сигнатуры ECDSA, а многие поставщики OIDC используют подписанные ECDSA JWT. [Yubico — один из немногих производителей WebAuthn, в дополнение к ECDSA поддерживающих более защищённый стандарт EdDSA. Сигнатуры EdDSA менее подвержены типу багов, описанных в статье.]
Если вы развернули в продакшене Java 15, Java 16, Java 17 или Java 18, то вам следует прекратить работу и немедленно обновиться, чтобы установить фиксы из апрельского Critical Patch Update.
Дополнение: в том же CPU устранены другие уязвимости защиты, поэтому (как обычно) стоит обновиться, даже если вы используете более старую версию Java. С другой стороны, в рекомендации OpenJDK как подверженные этой конкретной проблеме (CVE-2022–21449) перечислены только версии 15, 17 и 18.
Дополнение 2: компания Oracle сообщила мне, что находится в процессе корректирования рекомендации, в ней будет написано, что баг влияет только на версии 15–18. CVE уже был обновлён. Стоит заметить, что версии 15 и 16 больше не поддерживаются, поэтому как подверженные багу перечислены только 17 и 18.
Компания Oracle присвоила этому багу оценку CVSS 7.5, утверждая, что она не влияет на конфиденциальность и доступность. Наша компания ForgeRock оценила его на полные 10.0 из-за широкого влияния на различную функциональность в контексте управления доступом. Клиенты ForgeRock могут прочитать нашу рекомендацию о проблеме.
Контекст: сигнатуры ECDSA
ECDSA расшифровывается как Elliptic Curve Digital Signature Algorithm, этот алгоритм является широко используемым стандартом для подписывания всевозможных цифровых документов. По сравнению со старым стандартом RSA, ключи и сигнатуры на эллиптических кривых обычно гораздо меньше, обеспечивая при этом эквивалентную защиту, поэтому их широко применяют в тех случаях, когда размер важен. Например, стандарт WebAuthn для двухфакторной аутентификации позволяет производителям устройств выбирать из широкого ассортимента алгоритмов сигнатур, однако на практике почти все произведённые на данный момент устройства поддерживают только сигнатуры ECDSA (примечательным исключением является Windows Hello, в котором применяются сигнатуры RSA; предположительно, ради совместимости со старым оборудованием TPM).
Чтобы не вдаваться в технические детали, скажу, что сигнатура ECDSA состоит из двух значений. называемых r и s. Для проверки сигнатуры ECDSA используют уравнение, в котором задействованы r, s, публичный ключ подписывающего и хэш сообщения. Если обе части уравнения равны, то сигнатура действительна, в противном случае она отклоняется.
Одна часть уравнения — это r, а другая умножается на r и значение, полученное из s. Поэтому очевидно, что будет очень плохо, если r и s окажутся равными 0, потому что тогда мы будем проверять равенство 0 = 0 ⨉ [куча цифр], которое истинно вне зависимости от [кучи цифр]! А эта куча цифр — важная часть, например, сообщение и публичный ключ. Именно поэтому первым делом в алгоритме верификации ECDSA проверяется, что r и s >= 1.
Угадайте, какую проверку забыли разработчики Java?
Именно. В реализации верификации сигнатур ECDSA в Java не проверяются на равенство нулю r и s, поэтому можно создать значение сигнатуры, в котором они оба равны 0 (и соответствующим образом закодированы), а Java примет это как действительную сигнатуру для любого сообщения и любого публичного ключа. Это цифровой эквивалент пустого удостоверения личности.
Вот интерактивная сессия jshell, демонстрирующая уязвимую реализацию, которая принимает совершенно пустую сигнатуру в качестве действительной для произвольного сообщения и публичного ключа:
| Welcome to JShell -- Version 17.0.1
| For an introduction type: /help intro
jshell> import java.security.*
jshell> var keys = KeyPairGenerator.getInstance("EC").generateKeyPair()
keys ==> java.security.KeyPair@626b2d4a
jshell> var blankSignature = new byte[64]
blankSignature ==> byte[64] { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... , 0, 0, 0, 0, 0, 0, 0, 0 }
jshell> var sig = Signature.getInstance("SHA256WithECDSAInP1363Format")
sig ==> Signature object: SHA256WithECDSAInP1363Format
jshell> sig.initVerify(keys.getPublic())
jshell> sig.update("Hello, World".getBytes())
jshell> sig.verify(blankSignature)
$8 ==> true
// Ой, это не должно было верифицироваться...
Стоит заметить, что квалификатор InP1363Format лишь упрощает демонстрацию бага. Сигнатуры в формате ASN.1 DER можно эксплуатировать схожим образом, просто нужно для начала немного поиграться с кодировкой; однако учтите, что JWT и другие форматы используют сырой формат IEEE P1363.
Немного технических подробностей
Если вы изучите подробности ECDSA в Википедии, то увидите, что правая часть уравнения умножается не на s, а на его инверсию относительно умножения: s-1. Если вы немного знаете математику, то могли подумать «разве вычисление инверсии не приведёт к делению на ноль?» Однако в криптографии на эллиптических кривых эта инверсия вычисляется по модулю большого числа n, а для кривых, обычно применяемых в ECDSA, n — это простое число, поэтому мы можем использовать малую теорему Ферма для вычисления обратного по модулю числа:
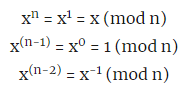
Это очень эффективно, и именно так поступает Java. Однако это действительно только при неравенстве x нулю, потому что ноль не имеет инверсии относительно умножения. Если x равен нулю, то 0(n-2) = 0: мусор на входе, мусор на выходе.
Из-за того, что вычисления выполняются по модулю n, также необходимо проверять, что r и s <n, потому что n = 0 (mod n) поэтому присвоение r или s значения n имело бы тот же эффект, что и присвоение им значения 0.
Ещё одна проверка, которая спасла бы Java — это проверка, описанная в шаге 5 алгоритма проверки в Википедии: проверка того, что точка, вычисленная из r и s, не является «точкой в бесконечности». Если r и s равны нулю, то получившаяся точка на самом деле будет точкой в бесконечности, поэтому эта проверка не пройдёт. Но Java не выполнила и эту проверку.
Почему это выяснилось только сейчас?
Возможно, вы задаётесь вопросом, почему это всплыло только сейчас, ведь поддержка ECDSA присутствовала в Java уже давно. Всегда ли она была уязвима?
Нет. Это относительно недавний баг, внесённый при переписывании кода EC с нативного C++ на Java, произошедшем в релизе Java 15. Хотя я уверен, что это переписывание кода дало преимущества в безопасности по памяти и удобству сопровождения, похоже, в реализации не принимали участие опытные криптографические разработчики. Исходная реализация на C++ неуязвима к таким багам, в отличие от переписанного кода. Ни та, ни другая реализация, похоже, не очень хорошо покрыта тестами, и даже самое поверхностное чтение спецификации ECDSA дало бы намёк на необходимость проверки на отбрасывание неверных значений r и s. Не уверен, что в коде не скрываются другие баги.
Что нам с этим делать?
Во-первых, если вы пользуетесь Java 15 или выше, то обновитесь до последней версии, чтобы получить фикс этой проблемы.
В общем случае, код криптографии очень сложно реализовать корректно, а алгоритмы сигнатур с публичным ключом — самые сложные в реализации. ECDSA — один из самых хрупких алгоритмов, в нём даже небольшая величина перекоса в одном случайном значении может привести к полному раскрытию приватного ключа. С другой стороны, у нас теперь есть такие превосходные ресурсы, как Project Wycheproof, предоставляющие наборы тестовых данных для известных уязвимостей. После того, как обнаружил этот баг, я обновил локальную копию Wycheproof и запустил проверку Java 17 — он мгновенно нашёл эту ошибку. Надеюсь, команда JDK будет использовать набор тестов Wycheproof, чтобы избежать проникновения подобных багов в код.
Если вы проектируете протокол или приложение, в котором, как вам кажется, необходимы цифровые сигнатуры, то подумайте, действительно ли они нужны — может быть, подойдёт более простой механизм? В простых алгоритмах MAC наподобие HMAC невероятно сложно запутаться по сравнению с системами сигнатур. Если вам действительно нужны сигнатуры, то подумайте об использовании современного алгоритма наподобие EdDSA, избегающего части ловушек ECDSA.
Хроника
11 ноября 2021 года — выявлена проблема и отправлен отчёт на адрес электронной почты OpenJDK для отчётов об уязвимостях.
11 ноября 2021 года — обнаружено изменение JDK, внёсшее баг в Java 15.
12 ноября 2021 года — отчёт принят Oracle.
18 ноября 2021 года — Oracle подтвердила баг и сообщила, что он будет пропатчен в будущем Critical Patch Update (CPU). Ему назначен ID трекинга S1559193.
18 ноября 2021 года — ForgeRock выпускает рекомендацию по безопасности, советующую нашим клиентам не разворачивать затронутые багом версии Java в продакшен.
14 января 2022 года — запрос к Oracle про обновление статуса. Получен ответ, что фикс планируется реализовать в апрельском CPU, который выпустят 19 апреля.
25 марта 2022 года — Oracle снова подтвердила, что фикс выйдет в апрельском CPU. ForgeRock проинформировала компанию, что полностью раскроет баг, если к тому времени он не будет устранён.
19 апреля 2022 года — фикс выпущен Oracle в апрельском CPU.
19 апреля 2022 года — опубликована статья.
