[Перевод] Автомат как реактивный двигатель: реальная физика нереального полёта
Перевод поста Malte Lenz «Machine Gun Jetpack: The Real Physics of Improbable Flight».Скачать файл с моделями, рассмотренными в посте, можно здесь здесь.Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
Можно ли летать с помощью автомата, используя реактивную силу, возникающую при выстрелах? Этот вопрос был задан в статье What if? Рэндалла Манроу «Machine Gun Jetpack.». Оказывается что можно, потому что некоторые автоматы создают достаточную силу для того, чтобы поднимать свой собственный вес, а может даже и немного больше. В этом посте я исследую динамику стреляющих вниз автоматов, а так же действующие при этом силы, порождаемые скорости и то, на какую высоту можно будет подняться таким способом. Я так же продублирую предупреждение из статьи: пожалуйста, не повторяйте этого дома. Для этого есть программные среды для моделирования.
Автомат с белкой на прикладеДавайте начнём с чего-то поменьше, чем человек. Например, с вот этой серой белки. Посадим белку на приклад, откроем огонь из автомата в автоматическом режиме и посмотрим, что же произойдёт. Для моделирования динамики этой системы я буду использовать Wolfram SystemModeler.
Модель автомата
На изображении выше можно увидеть автомат. Автомат как система состоит из патронов и самого автомата, притом они все обладают массами и подвержены воздействию гравитации. Их легко создать простым комбинированием встроенных механических компонентов:
Масса, под воздействием гравитационной силы Земли
Магазин является более сложным компонентом, потому что при каждом выстреле происходит выброс массы — самой пули и гильзы. При каждом выстреле из массы заряженного магазина вычитается масса пули и масса гильзы. То есть из начальной массы вычитается их масса, помноженная на количество выстрелов.
Объединив это с простенькой моделью белки, добавив датчик высоты над землёй и датчик столкновения, который при срабатывании завершает симуляцию, получим полную модель.
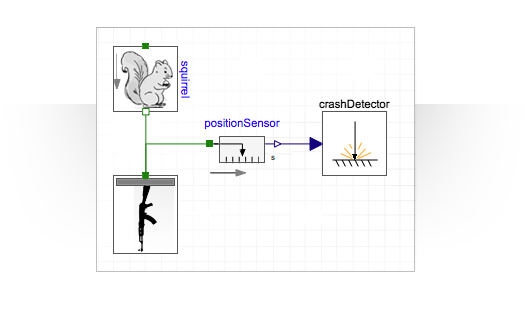
Чтобы корректно провести симуляцию, потребуется задать значения параметров различных компонентов. Я буду использовать серую белку, которая обычно весит около 0.5 кг.
Затем мне понадобятся данные по автомату. Я буду использовать вездесущий 7,62-мм автомат Калашникова (АК). Вот некоторые данные по нему:
Сгенерированная автоматом тяга может быть рассчитана исходя из массы пули, её дульной скорости и количества выстрелов в секунду:
Затем можно было бы оценить длительность каждого выстрела, то есть время, за которое пуля проходит через ствол. Введём допущение, что средняя скорость в стволе равна половине её дульной скорости:
Сила в этот момент времени может быть вычислена через тягу:
Теперь заданы все параметры, которые необходимы для моделирования полёта белки на автомате:
Проведём моделирование системы белка-автомат с одним патроном:
Если учесть, как будет изменяться высота в зависимости от времени, можно увидеть, что белка достигнет высоты в 9 сантиметров, а время полёта составит 0.27 секунды.
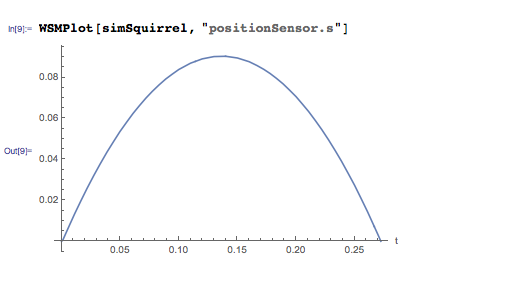
Или, говоря другими словами,
белка не особо-то и высоко поднялась. Какое очевидное решение этой проблемы? Конечно же, следует добавить патронов. Стандартный магазин содержит 30 штук:
Это даёт нам почти 5.8 секунд полёта, а белка поднимется до головокружительной высоты в 17.6 метров. Весьма пугающая высота для человека, но, пожалуй, не для белок.
Вот до какой высоты она долетела:
Я показал, что белка может летать, сидя на автомате. Давайте теперь посмотрим, как высоко сможет подлететь человек, если мы разрядим магазин в 30 патронов:
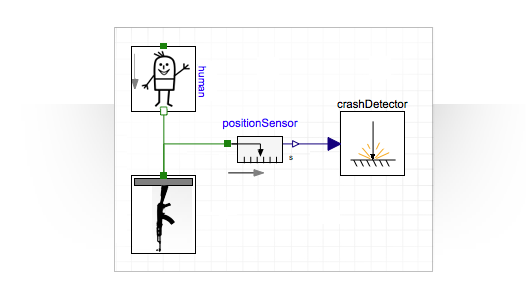
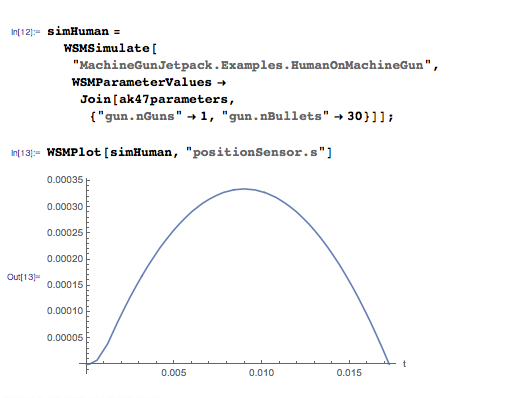
Одного автомата, пожалуй, маловато. Нужно взять их побольше. Введём параметр, который будет отвечать количеству автоматов и принимать значения в диапазоне от 1 до 80:
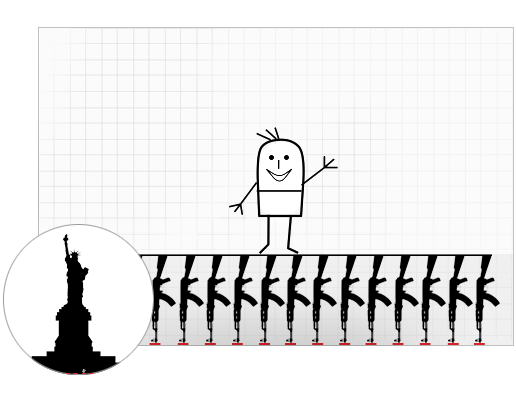
Тут есть кое-что интересное. Эффект от 50 автоматов и большего их количества легко может быть объяснён. Чем их больше, тем больше мощность, то есть и высота полёта будет выше. Однако симуляция с 15-ю и 32-мя автоматами немного интереснее. Давайте чуть более подробно рассмотрим вариант с 15-ю автоматами. Красные точки соответствуют моментам выстрелов, то есть автомат выстреливает по пуле каждые 100 мс:
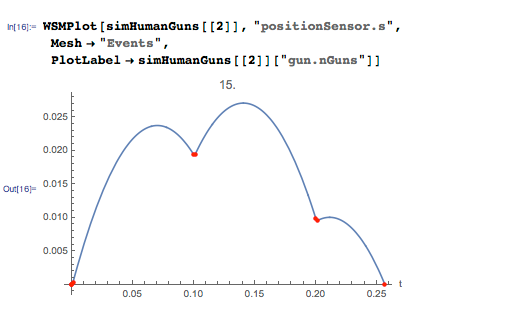
Можно увидеть, что вся эта система слегка подлетает, затем начинает падать, затем, после очередного выстрела, опять подлетает, но уже на несколько большую высоту, а потом опускается ниже, чем в предыдущий раз. Можно так же проследить за изменением скорости во времени:
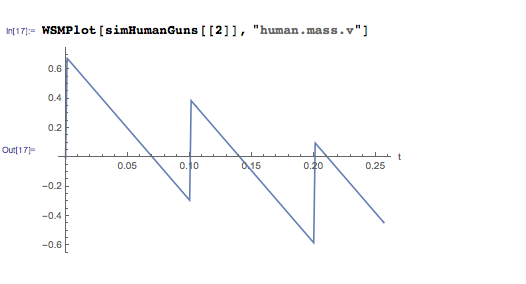
До первого выстрела вся система стоит на земле и, соответственно, обладает нулевой скоростью. Затем абсолютная скорость резко возрастает, однако до следующего выстрела успевает упасть ниже нуля. То есть после очередного залпа происходит падение скорости, в результате чего система начинает двигаться вниз, однако в магазине ещё есть патроны. Но далее будут происходить просто маленькие прыжки с места.
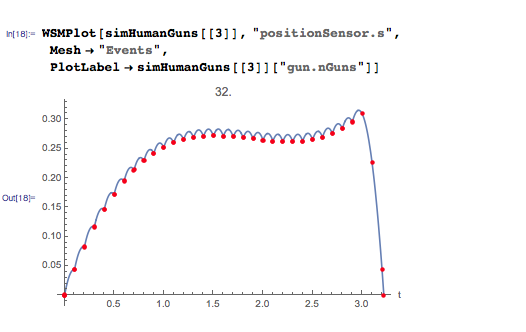
В сценарии с 32-мя автоматами наблюдается несколько другое поведение. Начало напоминает поведение системы с 15-ю автоматами — такое же ступенчатое, и абсолютная скорость с каждым залпом теряется, в результате чего система устремляется вниз. Однако где-то на 2.5 секундах после старта система начинает набирать высоту, пока все боеприпасы не будут израсходованы.
Это объясняется изменением массы магазина с течением времени:
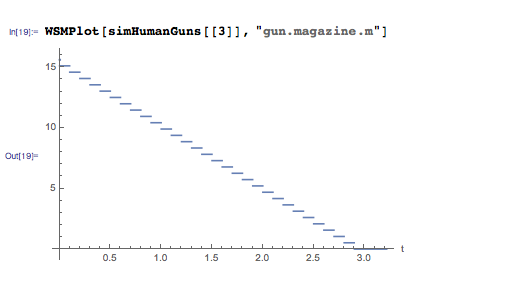
Можно увидеть, что при каждом выстреле магазин теряет массу — массу пули и гильзы. Из-за этого система становится достаточно лёгкой, чтобы начать набирать высоту. Это свидетельствует о том, что есть некоторый предел количества патронов, которыми можно снабдить каждый автомат при сохранении возможности полёта — ещё один интересный параметр, который можно варьировать. Давайте попробуем взлететь со следующими вместительностями магазина автомата:
Поскольку чем больше автоматов, тем больше мощности, то возьмём, скажем, тысячу штук:
Если взять тысячу автоматов, то оказывается, что снабдить каждый 165-ю патронами — не лучший вариант:
Это происходит потому, что если взять слишком много пуль, то система станет слишком тяжелой для полётов. Теперь, когда я получил обоснованное (если это слово вообще применимо к полётам на автоматах) количество патронов для полёта, давайте посмотрим, какая высота сможет быть достигнута при изменении количества автоматов. Можно было бы ожидать, что чем больше автоматов, то тем выше будет полёт и больше время полёта.
Вот зависимость максимальных высот от количества автоматов:
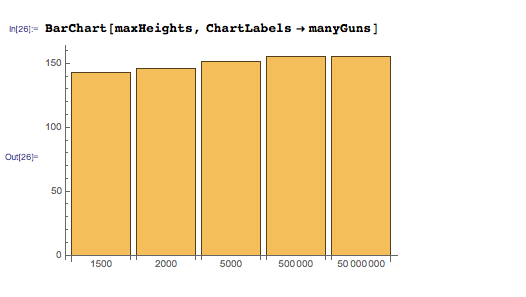
Как оказывается, значительное увеличение числа автоматов (с 1500 до 50 миллионов) даёт весьма незначительный прирост максимальной высоты. Это происходит потому, что число автоматов возрастает, удельный вес человека на каждый автомат уменьшается, пока каждый автомат не будет поднимать лишь свою собственную массу с небольшой дополнительной массой. Получается, что система сможет достичь той же максимальной высоты, что и один единственный автомат, но без дополнительной массы, и увеличение количества автоматов перестаёт давать какие-то преимущества.
Обобщим вышесказанное: лучший реактивный двигатель из автоматов должен содержать как минимум 5000 АК со 145-ю патронами в магазине.
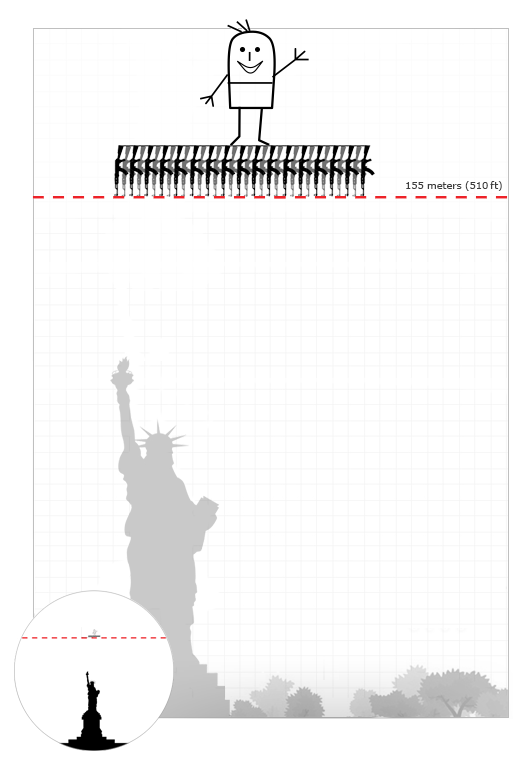Как высоко можно подлететь с помощью автоматов
