[Перевод] Арбелос
 Скачать статью в виде документа Mathematica (NB), CDF-файла или PDF.Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
В этой статье систематически проверяются некоторые свойства фигуры, известной с древних времён, называемой арбелос. Она включает в себя несколько новых открытий и обобщений, представленных автором данной работы.Введение
Будучи мотивирован вычислительными преимуществами, которыми обладает Mathematica, некоторое время назад я решил приступить к исследованию свойств арбелоса — весьма интересной геометрической фигуры. С тех пор я был впечатлен большим количеством удивительных открытий и вычислительных проблем, которые возникали из-за всё расширяющегося объёма литературы, касающейся этого примечательного объекта. Я вспоминаю его сходство с нижней частью культового велосипеда пенни-фартинг из The Prisoner (телесериал 1960-х), шутовской шапкой Панча (знаменитых Punch and Judy) и символом инь-ян с одной перевёрнутой дугой; см. рис. 1. В настоящее время существует специализированный каталог архимедовых кругов (круги, содержащиеся в арбелосе) [1] и важные применения свойств арбелоса, которые лежат вне поля математики и вычислительных наук [2].Многие известные исследователи занимались этой темой, в том числе Архимед (убитый римским солдатом в 212 г. до н.э.), Папп (320 г. н.э.), Кристиан О. Мор (1835–1918), Виктор Тебо (1882–1960), Леон Банкофф (1908–1997), Мартин Гарднер (1914–2010). С недавних пор свойствами арбелоса занимаются Клейтон Додж, Питер Ай. Ву, Томас Шох, Хироши Окумура, Масаюки Ватанабе и прочие.
Скачать статью в виде документа Mathematica (NB), CDF-файла или PDF.Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
В этой статье систематически проверяются некоторые свойства фигуры, известной с древних времён, называемой арбелос. Она включает в себя несколько новых открытий и обобщений, представленных автором данной работы.Введение
Будучи мотивирован вычислительными преимуществами, которыми обладает Mathematica, некоторое время назад я решил приступить к исследованию свойств арбелоса — весьма интересной геометрической фигуры. С тех пор я был впечатлен большим количеством удивительных открытий и вычислительных проблем, которые возникали из-за всё расширяющегося объёма литературы, касающейся этого примечательного объекта. Я вспоминаю его сходство с нижней частью культового велосипеда пенни-фартинг из The Prisoner (телесериал 1960-х), шутовской шапкой Панча (знаменитых Punch and Judy) и символом инь-ян с одной перевёрнутой дугой; см. рис. 1. В настоящее время существует специализированный каталог архимедовых кругов (круги, содержащиеся в арбелосе) [1] и важные применения свойств арбелоса, которые лежат вне поля математики и вычислительных наук [2].Многие известные исследователи занимались этой темой, в том числе Архимед (убитый римским солдатом в 212 г. до н.э.), Папп (320 г. н.э.), Кристиан О. Мор (1835–1918), Виктор Тебо (1882–1960), Леон Банкофф (1908–1997), Мартин Гарднер (1914–2010). С недавних пор свойствами арбелоса занимаются Клейтон Додж, Питер Ай. Ву, Томас Шох, Хироши Окумура, Масаюки Ватанабе и прочие.
Леон Банкофф — человек, который привлекал всеобщее внимание к арбелосу в последние 30 лет. Шох привлёк внимание Бэнкоффа к арбелосу в 1979 году, открыв несколько новых архимедовых кругов. Он послал 20-страничную рукописную работу Мартину Гарднеру, который направил её Бэнкоффу, который затем отправил 10-страничный фрагмент копии рукописи Доджу в 1996 году. Из-за смерти Бэнкоффа запланированная совместная работа была прервана, пока Додж не сообщил о некоторых новых открытиях [3]. В 1999 году Додж сказал, что ему потребуется от пяти до десяти лет, чтобы отсортировать весь материал, которым он располагает, разложив всё это дело по стопкам. В настоящее время эта работа все ещё продолжается. Не удивительно, что в четвертом томе The Art of Computer Programming, сказано о том, что важная работа требует большого количества времени.
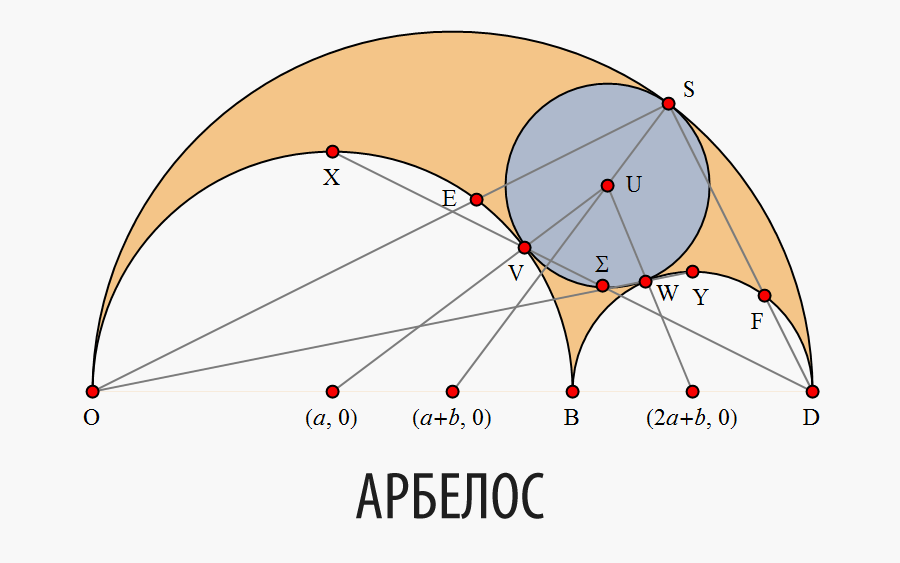
 Рис. 1. Велосипед пенни-фартинг, куклы Панч и Джуди, физический арбелос.
Рис. 1. Велосипед пенни-фартинг, куклы Панч и Джуди, физический арбелос.
Арбелос («нож сапожника» в греческом языке) назван так из-за своего сходства с лезвием ножа, использующегося сапожниками (Рис. 1). Арбелос — плоская область, ограниченная тремя полуокружностями и общей базовой линией (рис. 2). Архимед, вероятно, был первым, кто начал изучать математические свойства арбелоса. Эти свойства описаны в теоремах с 4-ой по 8-ую его книги Liber assumptorum (или Книги лемм). Возможно, эту работу написал не Архимед. Сомнения появились после перевода с арабского Книги лемм, в которой Архимед упоминается неоднократно, но ничего не сказано о его авторстве (однако, существует мнение, что эта книга — подделка [4]). Книга Лемм так же содержит знаменитую архимедову Problema Bovinum [5].
Эта статья направлена на систематическое изложение некоторых свойств арбелоса и не носит исчерпывающий характер. Наша цель состоит в том, чтобы выработать единую вычислительную методологию для того, чтобы преподнести данные свойства в формате обучающей статьи. Все свойства выстроены в рамках определённой последовательности и представлены с доказательствами. Эти доказательства были реализованы посредством тестирования эквивалентных вычисляемых утверждений. В ходе выполнения данной работы автором было совершено несколько открытий и сделано несколько обобщений.Мы называем наибольший полукруг верхней дугой, а два маленьких — левосторонней и правосторонней дугами, или просто боковыми дугами, если нет необходимости их различать. Мы используем 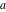 и
и  соответственно для обозначения их радиусов, а радиус верхней дуги обозначается как
соответственно для обозначения их радиусов, а радиус верхней дуги обозначается как  . Отрезок между двумя точками неориентирован и простирается от одной точки до другой, в то время как прямая, содержащая две точки, является бесконечной и находится и за пределами этих двух точек. Классическая неточность в обозначениях — использовать
. Отрезок между двумя точками неориентирован и простирается от одной точки до другой, в то время как прямая, содержащая две точки, является бесконечной и находится и за пределами этих двух точек. Классическая неточность в обозначениях — использовать  для обозначения как самого отрезка, соединяющего точки
для обозначения как самого отрезка, соединяющего точки 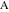 и
и 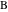 , так и его длины в зависимости от контекста; современная нотация велит писать
, так и его длины в зависимости от контекста; современная нотация велит писать  для обозначения длины отрезка.
для обозначения длины отрезка.
Эта функция задаёт арбелос.
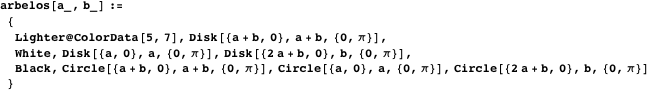
Так можно нарисовать сам арбелос.

 Рис 2. Арбелос.
Рис 2. Арбелос.
Свойство 1Периметр арбелоса равен периметру наибольшей окружности.
Свойство 2Площадь арбелоса равна площади круга с диаметром 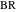 .
.
Это лемма под номером 4 из Книги лемм (рис. 3) [7, 8].
Эти два свойства легко доказываются путём вычисления представленной ниже логической конструкции, состоящей из двух равенств.


Функция drawpoints отображает заданные точки красными кружками.
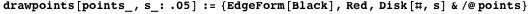

 Рис. 3. Площадь круга диаметра
Рис. 3. Площадь круга диаметра  (радикального круга) равна площади арбелоса.
(радикального круга) равна площади арбелоса.
Радикальный круг
Круг на риc. 3 называется радикальным кругом арбелоса, а линия 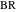 называется его радикальной осью (эта терминология будет разъяснена в Обобщениях). Обозначим и проименуем точки, линии, окружности и координаты, которые нам понадобятся для иллюстрации свойств 3–11 и 25–26 (рис. 4).
называется его радикальной осью (эта терминология будет разъяснена в Обобщениях). Обозначим и проименуем точки, линии, окружности и координаты, которые нам понадобятся для иллюстрации свойств 3–11 и 25–26 (рис. 4).
 Рис. 4. Обозначения координат, линий и окружностей, упомянутых в свойствах 3–11 и 25–26.
Рис. 4. Обозначения координат, линий и окружностей, упомянутых в свойствах 3–11 и 25–26.
Свойство 3Линии 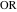 и
и  перпендикулярны и касаются боковых дуг в точках
перпендикулярны и касаются боковых дуг в точках  и
и 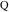 , пересекая их общую касательную.
, пересекая их общую касательную.
Чтобы доказать перпендикулярность линий 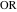 и
и  , вычислим скалярное произведение векторов
, вычислим скалярное произведение векторов 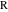 и
и  .
.
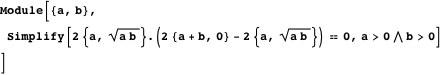

Используем полученный результат для получения угла наклона прямой 
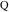 .
.
Теорема 1Уравнение касательной к левой дуге в точке 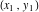 :
:
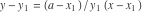
а уравнение касательной к правой дуге в точке 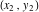 :
:
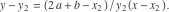
Функция PQ находит координаты точек касания  и
и 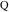 путём решения системы из четырех уравнений, которые задают их положения на дугах и углы наклона касательных согласно теореме 1.
путём решения системы из четырех уравнений, которые задают их положения на дугах и углы наклона касательных согласно теореме 1.
Помимо PQ, в данной статье встречаются так же и нижеперечисленные обозначения точек и величин: VWS, HK, U, EF, IJr и LM.
Функция dSq вычисляет квадрат расстояния между двумя заданными точками.



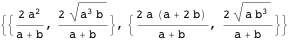
Свойство 4Точки  и
и 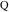 находятся на радикальной окружности.
находятся на радикальной окружности.
Так как 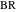 является диаметром радикальной окружности, нам нужно всего лишь доказать равенство расстояний от
является диаметром радикальной окружности, нам нужно всего лишь доказать равенство расстояний от  и
и 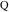 до центра радикальной окружности, который обозначается как
до центра радикальной окружности, который обозначается как  .
.


Свойство 5Пусть линия 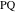 пересекает верхнюю дугу в точках
пересекает верхнюю дугу в точках 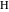 и
и 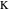 . Тогда
. Тогда 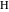 и
и 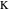 лежат на окружности c центром в
лежат на окружности c центром в 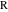 и радиусом
и радиусом 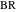 .
.
Мы получаем координаты точек 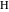 и
и 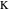 , решая систему уравнений, которая задаёт их расположение на верхней дуге и на линии
, решая систему уравнений, которая задаёт их расположение на верхней дуге и на линии 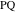 .
.

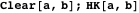

Это доказывает свойство 5 путём проверки того, что расстояния от 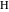 и
и 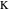 до
до 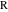 равны расстоянию от
равны расстоянию от 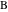 до
до 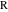 .
.
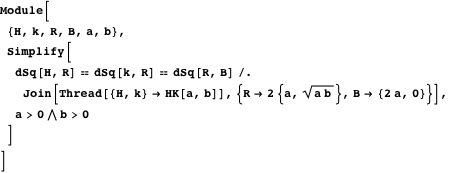

Свойство 6Прямая 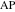 параллельна прямой
параллельна прямой 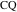 .
.
Это эквивалентно тому, что определитель векторов 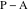 и
и  (их векторное произведение) равен нулю.
(их векторное произведение) равен нулю.


Свойство 7Прямая 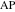 перпендикулярна прямой
перпендикулярна прямой 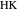 .
.
Это эквивалентно тому, что скалярное произведение векторов 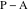 и
и 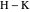 равно нулю.
равно нулю.


Обозначим окружность с центром в 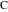 и радиусом
и радиусом 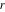 как
как 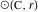 .
.
Свойство 8Пары  ,
,  и
и 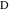 ,
, 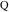 — представляют собой пары взаимно обратных точек для окружности
— представляют собой пары взаимно обратных точек для окружности  .
.
Обратной точкой к точке 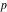 в окружности
в окружности 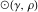 (при этом
(при этом 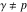 ) является такая точка
) является такая точка  , что выполняется равенство
, что выполняется равенство  [9]. Функция inversion реализует эту идею.
[9]. Функция inversion реализует эту идею.
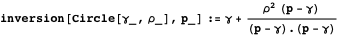
Так можно доказать свойство 8, подставив 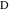 вместо
вместо 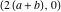 .
.


Свойство 9Исследуем окружность обратных точек  . Для данной окружности точки
. Для данной окружности точки 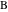 ,
, 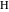 ,
, 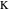 совпадают со своими обратными точками. Отрезок
совпадают со своими обратными точками. Отрезок  является обратным для дуги
является обратным для дуги 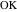 , а отрезок
, а отрезок  — инверсия дуги
— инверсия дуги 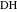 . Дуги
. Дуги  и
и 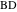 так же являются взаимно обратными. Радикальная окружность есть инверсия прямой
так же являются взаимно обратными. Радикальная окружность есть инверсия прямой 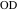 .
.
Свойство 10Прямые 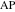 и
и 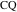 есть касательные к радикальной окружности.
есть касательные к радикальной окружности.
Это утверждение аналогично тому, что соответствующие дуги (то есть их касательные) перпендикулярны радакальной окружности (его касательным в точках пересечения). Согласно свойству 8, дуги являются перпендикулярными окружности с диаметром 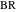 , если они проходят через пару обратных точек [10,11].
, если они проходят через пару обратных точек [10,11].
Свойство 11 — прямоугольник.
— прямоугольник.
Это один из сюрпризов Бэнкоффа (Bankoff«s surprises) [12,13,14]. Если все четыре точки лежат на радикальной окружности, нам достаточно доказать, что 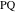 делит пополам
делит пополам 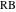 .
.


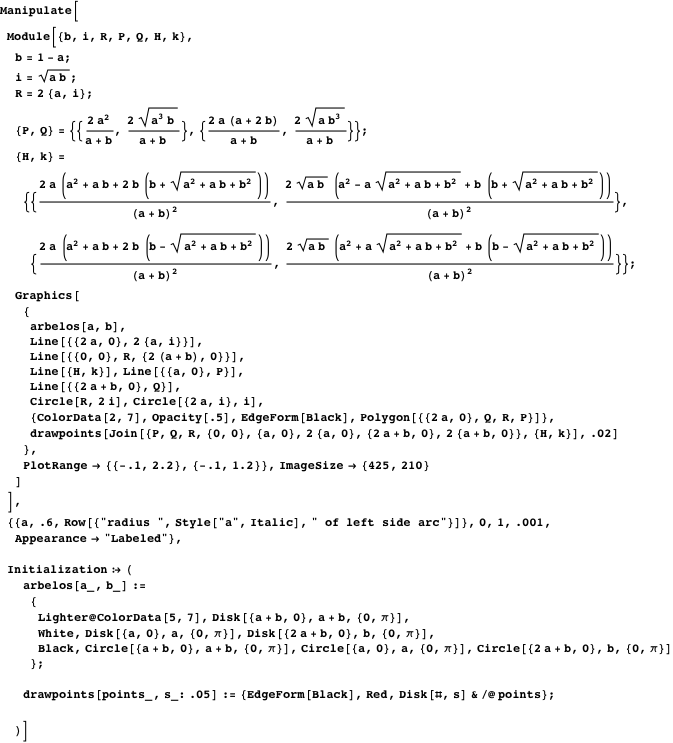
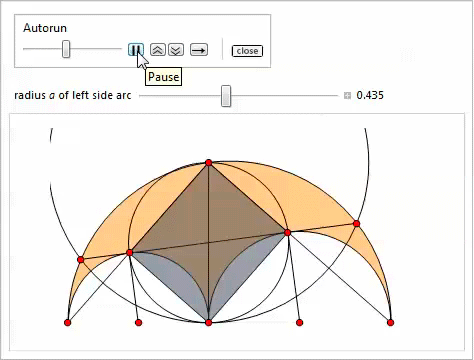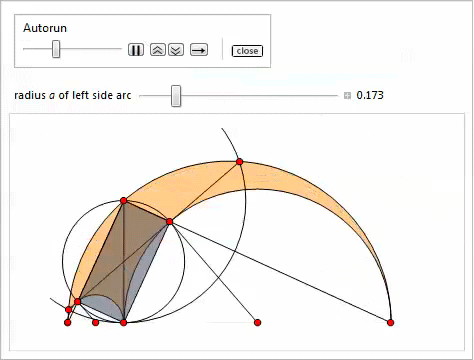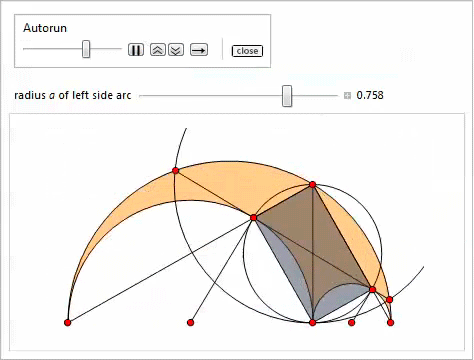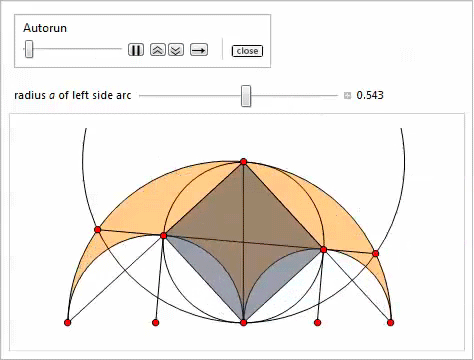
Представленная ниже демонстрация со слайдером (реализованным посредством функции Manipulate) иллюстрирует свойства 3–11. Самый лёгкий способ задать точки P, Q, H, K — скопировать и вставить соответствующие для них формулы.
Вписанная окружность
Теперь рассмотрим окружность, касательную к боковым дугам и верхней дуге — вписанную окружность 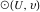 в арбелос с точками касания
в арбелос с точками касания 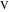 ,
, 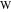 , и
, и  (см. рис. 5) [15, 16]. Обозначим так же вершины дуг точками
(см. рис. 5) [15, 16]. Обозначим так же вершины дуг точками 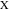 и
и 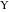 соответственно.
соответственно.
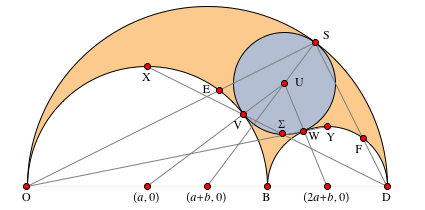 Рис. 5. Вписанная окружность
Рис. 5. Вписанная окружность  , координаты, прямые и точки, указанные на рисунке, фигурируют в свойствах с 12 по 15.
, координаты, прямые и точки, указанные на рисунке, фигурируют в свойствах с 12 по 15.
Шестое утверждение из Книги лемм включает так же радиус вписанной окружности, обозначаемый как  . Функция U
. Функция U вычисляет координаты центра
вычисляет координаты центра  вписанной окружности и её радиус
вписанной окружности и её радиус  .
.
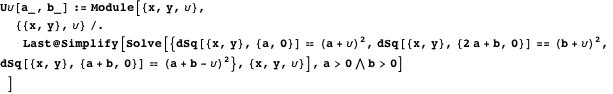
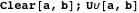
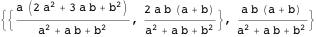
Координаты точек касания 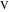 ,
, 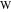 , и
, и  определяются через пересечение линий, соединяющих центры дуг арбелоса, со вписанной окружностью.
определяются через пересечение линий, соединяющих центры дуг арбелоса, со вписанной окружностью.
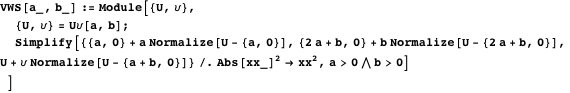

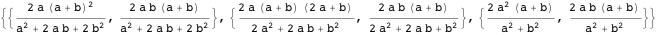
Свойство 12Точки 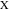 ,
, 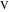 , и
, и 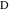 лежат на одной прямой. Точки
лежат на одной прямой. Точки  ,
, 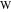 , и
, и 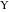 лежат на одной прямой. Линии
лежат на одной прямой. Линии 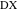 и
и  пересекаются в точке
пересекаются в точке  , которая лежит на вписанной окружности.
, которая лежит на вписанной окружности.
Первые два утверждения можно доказать, используя критерий определителя для проверки коллинеарности.
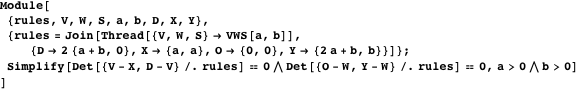

Пусть  будет точкой пересечения линий
будет точкой пересечения линий 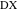 и
и  . Доказав, что расстояние от этой точки до
. Доказав, что расстояние от этой точки до  равно
равно  , мы докажем третье утверждение.
, мы докажем третье утверждение.
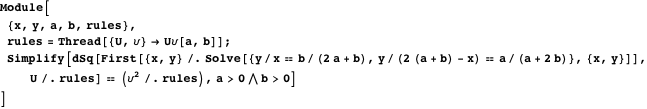

Свойство 13Точки  ,
, 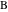 ,
, 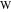 , и
, и лежат на окружности с центром в
лежат на окружности с центром в 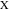 . Аналогично, точки
. Аналогично, точки 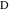 ,
, 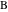 ,
, 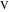 , и
, и  лежат на окружности с центром в
лежат на окружности с центром в 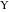 .
.
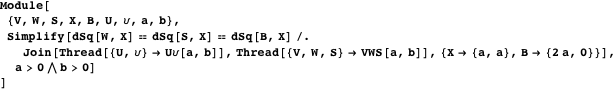

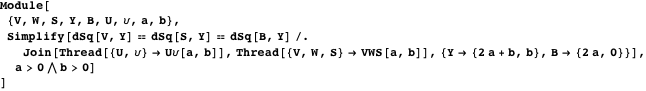

Представленная ниже демонстрация с Manipulate иллюстрирует свойство 13 [17]. Опция Bankoff circle покажет вписанную окружность в треугольник, который соединяет центры дуг. Это иллюстрирует свойство 23.

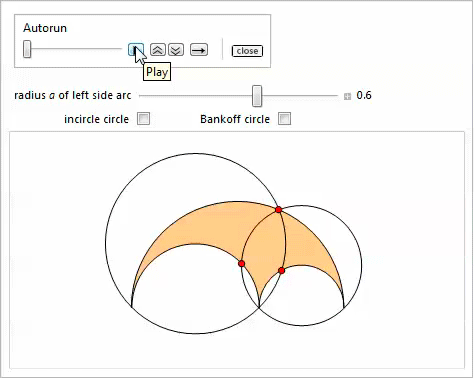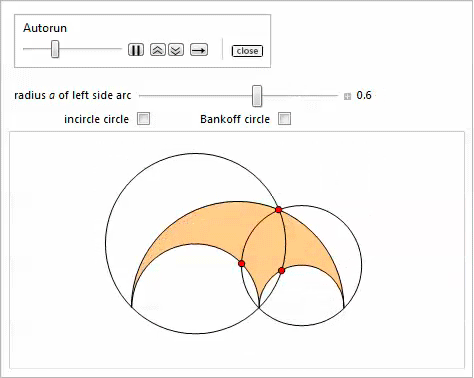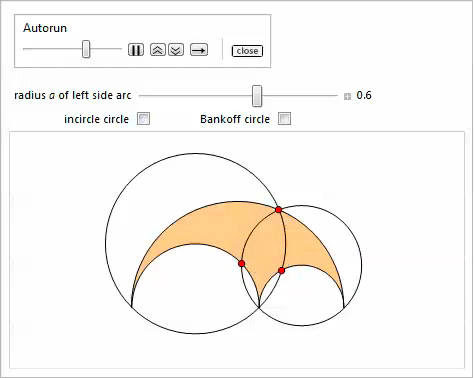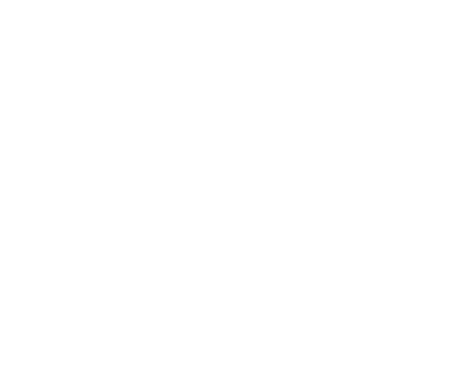
Свойство 14Пусть  — диаметр вписанной окружности, параллельный
— диаметр вписанной окружности, параллельный 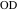 , а
, а  — проекция
— проекция  на
на 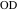 . Прямоугольник между отрезками
. Прямоугольник между отрезками  и
и  — квадрат.
— квадрат.
Данное свойство проиллюстрировано в следующей демонстрации с Manipulate и легко может быть проверена следующим выражением.
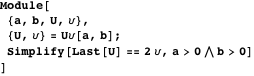

Свойство 15Пусть  и
и 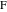 — пересечения линий
— пересечения линий  и
и  с боковыми дугами. Тогда
с боковыми дугами. Тогда 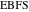 — квадрат практически такого же размера, что и квадрат, который упоминался в свойстве 14.
— квадрат практически такого же размера, что и квадрат, который упоминался в свойстве 14.
Сперва получим точки  и
и 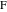 как пересечения соответствующих линий и дуг, а затем сохраним результат в переменной replaceEF.
как пересечения соответствующих линий и дуг, а затем сохраним результат в переменной replaceEF.

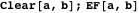

Докажем свойство 15, сделав  равным вектору, получаемому вращением
равным вектору, получаемому вращением  вокруг
вокруг 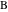 на 90° и сделав
на 90° и сделав  равным вектору, получаемому перемещением
равным вектору, получаемому перемещением  через
через  .
.


Учитывая  и
и 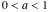 , нижеследующий график сравнивает размеры двух квадратов.
, нижеследующий график сравнивает размеры двух квадратов.
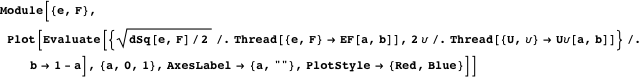

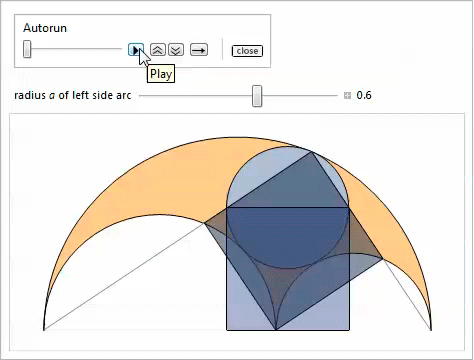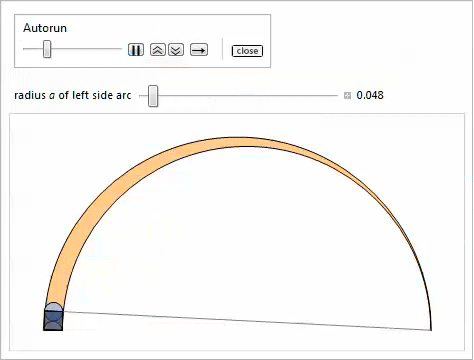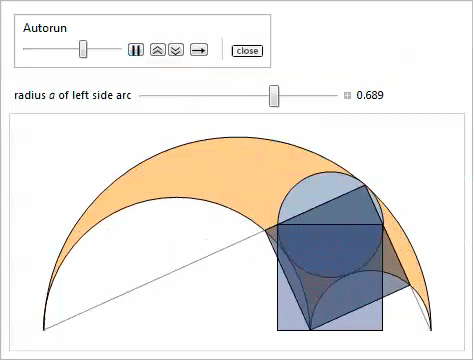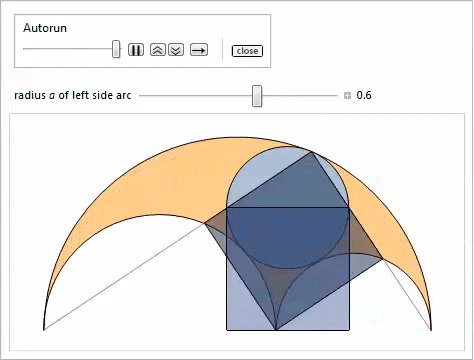
Демонстрация с Manipulate иллюстрирует свойства 14 и 15.

Близнецы
Рассмотрим два серых круга, которые касаются радикальной оси, а так же боковые и верхние дуги на рис. 6. Они называются близнецами, или архимедовыми окружностями. В связи с нижеследующим замечательным свойством, они были хорошо изучены. Множество их необычных черт были освещены в нашем списке свойств [3, 18, 19].
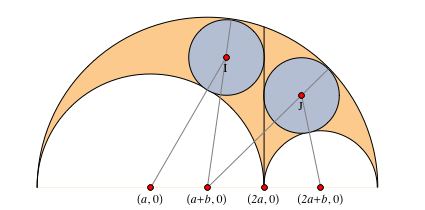 Рис. 6. Близнецы.
Рис. 6. Близнецы.
Свойство 16Два круга, которые перпендикулярны радикальной оси, верхней и боковым дугам арбелоса имеют одинаковый радиус.
Это свойство идёт как пятое утверждение в Книге лемм. Решая данную систему из шести уравнений, мы находим значения их радиусов, проверяем, что они равны и находим координаты их центров 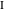 ,
, 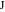 .
.


Эти четыре решения дают центры, сгруппированные попарно: 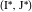 ,
, 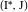 ,
, 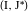 ,
,  где
где 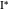 и
и 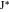 являются отображениями
являются отображениями 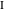 и
и 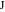 на диаметр арбелоса; только последнее выражение является допустимым. Это так же показывает, что близнецы действительно одного и того же радиуса
на диаметр арбелоса; только последнее выражение является допустимым. Это так же показывает, что близнецы действительно одного и того же радиуса 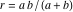 . Любая окружность, у которой радиус имеет ту же длину, что и у близнецов, называется архимедовой. Можно провести довольно наглядную аналогию для
. Любая окружность, у которой радиус имеет ту же длину, что и у близнецов, называется архимедовой. Можно провести довольно наглядную аналогию для 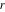 , если представить, что
, если представить, что 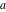 и
и  — (электрические) сопротивления. Тогда
— (электрические) сопротивления. Тогда 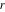 — сопротивление, получаемое путём параллельного соединения
— сопротивление, получаемое путём параллельного соединения 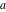 и
и  ; то есть
; то есть 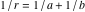 . Функция IJr вычисляет координаты центров и длину радиуса близнецов.
. Функция IJr вычисляет координаты центров и длину радиуса близнецов.
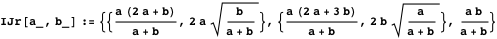
Свойство 17Площадь арбелоса равна площади наименьшего круга, который охватывает близнецов.
Рассмотрим окружность, касательную к обоим близнецам, с центром в точке 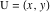 и радиусом
и радиусом  . Тогда у нас будут два возможных значения для
. Тогда у нас будут два возможных значения для  .
.
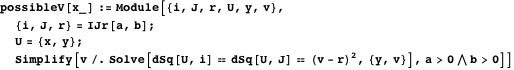

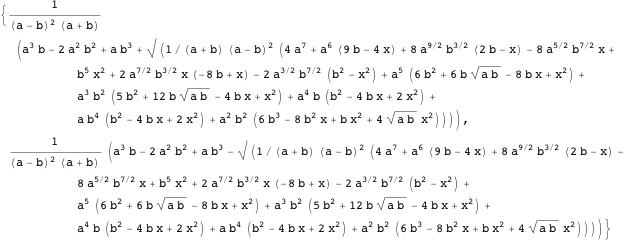
Чтобы найти экстремум для  , приравняем производные обоих уравнений к нулю и решим их относительно
, приравняем производные обоих уравнений к нулю и решим их относительно 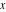 .
.
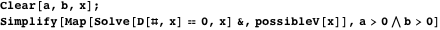
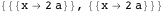
Таким образом, центры наименьшей и наибольшей окружностей, касательных к близнецам, лежат на радикальной оси. Более того, их центры лежат в одной точке, что следует из решения данного выражения.
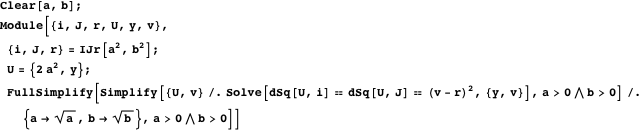
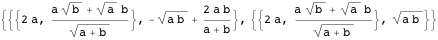
Таким образом, используя свойство 2, мы доказываем, что наибольшая касательная окружность, которая является самой малой из тех, что содержит близнецов, удовлетворяет свойству 17. Нижеследующая демонстрация с Manipulate показывает окружности, касательные к близнецам, при этом можно регулировать радиус 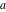 левой боковой дуги.
левой боковой дуги.


Следующий график сравнивает радиусы двух окружностей, касательных к близнецам, с центрами на радикальной оси.
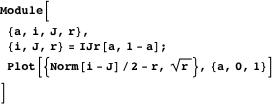
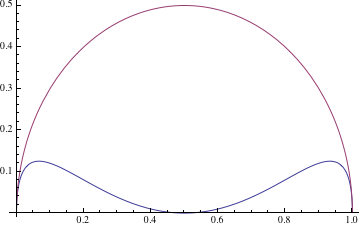

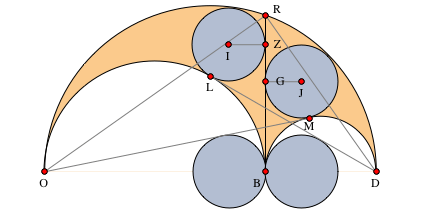 Рис. 7. Обозначения точек и отрезков, которые будут фигурировать в свойствах 18–24.
Рис. 7. Обозначения точек и отрезков, которые будут фигурировать в свойствах 18–24.
Свойство 18Общая касательная к левой дуге и близнецу (точка касания —  ) проходит через точку
) проходит через точку 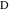 . Аналогично, общая касательная к правой дуге и близнецу (точка касания —
. Аналогично, общая касательная к правой дуге и близнецу (точка касания — 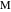 ) проходит через точку
) проходит через точку  (см. рис. 7).
(см. рис. 7).
Т
