[Из песочницы] Загадка фликкер-шума разгадана
Давным-давно, когда диоды были ещё вакуумными, J.В. Johnson впервые наблюдал мерцательный эффект в токе электронных ламп, который он так и назвал — мерцательным или фликкер-шумом. Прошло ровно 90 лет с тех пор, а фликкер-шум продолжают обнаруживать в самых разнообразных системах — от полупроводниковых приборов до разлива рек, от физики до социологии, но объяснить природу его происхождения так никто и не смог.
Даже советский фильм есть про фликкер-шум.
Вот как выглядит фликкер-шум: 
Физики, пытаясь объяснить природу данного явления, естественно, ищут её в физике протекающих процессов, хотя и называют фликкер-шум аномалией. Вспомним, чему нас учат в аспирантуре на курсах по «Истории и философии науки»: аномалия (чем и является фликкер-шум) — это результат принципиальной неспособности научной парадигмы объяснить существующие факты, то есть проблему необходимо искать в теории.
Теорией в данном случае являются спектральные методы. Попробуем разобраться с этими методами, может с ними что-то не так?
По определению, фликкер-шум является сигналом, спектральная плотность мощности (или просто спектр мощности) которого описывается формулой:
где K — размерная константа, γ — безразмерная константа, которая в большинстве случаев близка к единице (в статье будем рассматривать только фликкер-шум с γ = 1).
Посмотрим на спектр мощности фликкер-шума и попробуем в нём что-нибудь увидеть.
Видно, что мощность в полосе частот от 1 Гц до бесконечности равна мощности от 0 до 1 Гц. Что такого особенного в этих двух полосах частот, что мощность в них одинаковая? Эти две полосы связывает то, что их границы являются обратными величинами друг друга, то есть 0 равен 1/бесконечность, а 1 равна 1/1. А что такое обратная величина от частоты? Это период.
Интересно, а почему в спектральном анализе используется только спектральная плотность мощности по частоте, может стоит попробовать найти спектральную плотность мощности по периоду? На этом месте все говорят — «зачем нужно от периода находить, от этого ничего не изменится». Посмотрите на рисунок.
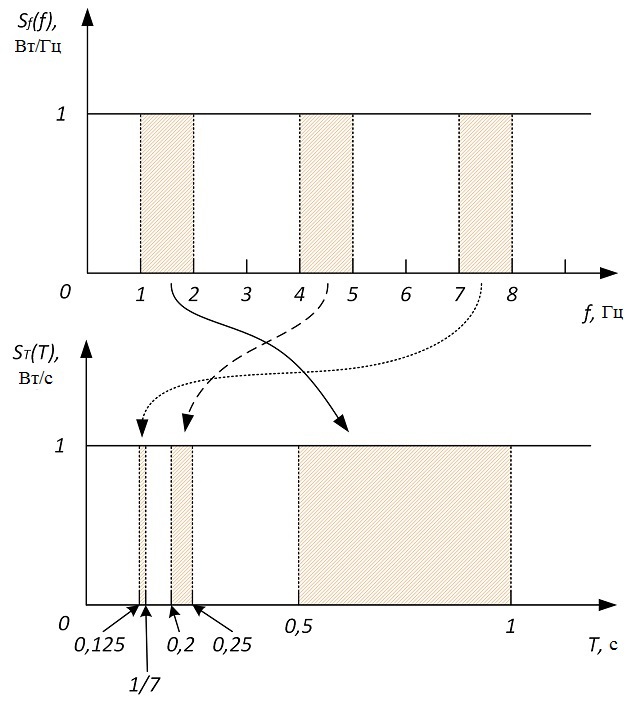
Из рисунка видно, что одной и той же полосе частот соответствуют разные полосы периодов. Значит, спектр мощности по периоду должен быть совсем другой формы. Найдём связь между спектральными плотностями мощности по частоте и по периоду. Элементарное приращение мощности равно: 
где Sf (f) — спектральная плотность мощности по частоте (f-СПМ), ST (f) — спектральная плотность мощности по периоду (T-СПМ), T — период.
Знак минуса в правой части формулы (2) означает, что положительному приращению по частоте соответствует отрицательное приращение по периоду.
Из формулы (2) получим:
Как же теперь будет выглядеть фликкер-шум? Опять то же самое:
Фликкер-шум является единственным сигналом, спектр мощности которого выглядит одинаково как по частоте, так и по периоду. Если взять, к примеру, белый шум, то его T-СПМ не будет уже равномерной по периоду:
Какой же тогда сигнал будет равномерным по периоду? Да вот какой:
Это броуновский шум, его T-СПМ и f-СПМ, соответственно, определяются формулами:
Если представлять броуновский шум в виде суммы гармоник, то удобнее использовать тогда не ряд Фурье, а ряд с равномерным шагом по периоду:
где An — амплитуда n-ой гармоники, T1 — период основной гармоники, φn — фаза n-ой гармоники.
Можно ещё анимацию с суммированием гармоник сделать:
Со спектральной плотностью мощности по периоду можно ещё долго экспериментировать, но будем двигаться дальше.
Одинаково равномерным по частоте и по периоду, исходя из формулы (4), может быть только сигнал, всюду равный нулю. Какой же шум тогда считать сигналом с равномерным спектром? Попробуем вообразить сигнал с равномерным спектром и при этом не привязываться к какому-либо шагу по частоте или по периоду.
Представим, что какой-то завод выпускает генераторы синусоидального напряжения фиксированной частоты и фиксированной мощности. Все выпускаемые генераторы обладают абсолютной повторяемостью по мощности генерируемого сигнала и эта мощность равна P0. Однако повторяемость по частоте отсутствует напрочь — частота у каждого генератора может быть равна любому значению от нуля до бесконечности (хоть пГц, хоть ТГц). Теперь возьмём очень большое количество таких генераторов и подадим сигналы с их выходов на сумматор.
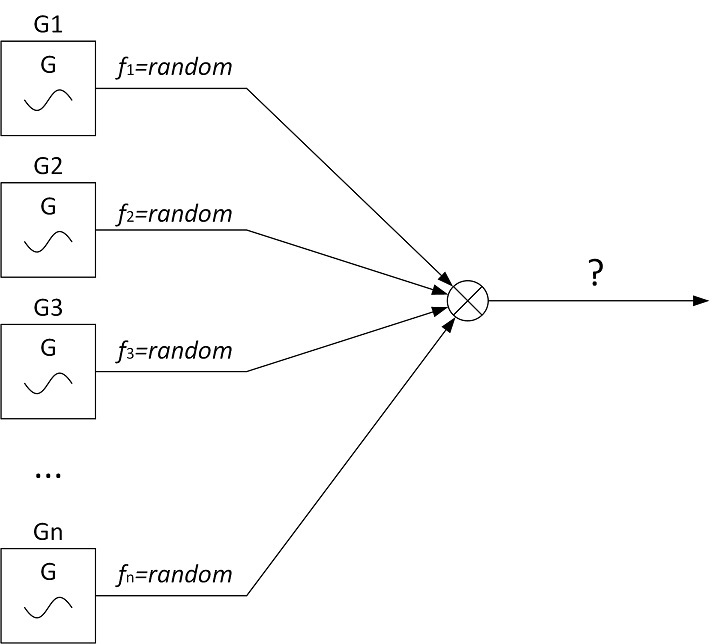
Здесь рассматривается такой процесс с бесконечной энергией, что каждая его реализация содержит только одну гармонику, при этом, мощность каждой реализации равна P0, а частота может принимать любое значение.
Очевидно, что сигнал на выходе сумматора должен обладать равномерным спектром. Какой же будет у него спектр мощности?
Каждый, кто знаком с основами спектрального анализа, сразу выдаст ответ — «это белый шум, так как он по определению является сигналом с равномерным спектром». Давайте это проверим.
Для начала, нужно каким-то образом связать мощность каждого генератора с его частотой. В этом месте может возникнуть вопрос — «что тут связывать, если она не зависит от частоты?», тогда встречный вопрос — от периода она тоже не зависит? В качестве такого связующего звена можно использовать энергию одного периода синусоиды:
Мощность генератора равна:
Теперь найдём функцию, которая будет показывать зависимость мощности генераторов от их частоты:
где ET (f) — зависимость энергии периода синусоиды генератора от частоты.
Мощность в полосе частот от нуля до f определяется формулой (12), мощность в полосе частот от нуля до (f+df) определяется формулой:
тогда мощность, приходящаяся на полосу частот df, будет равна:
Если посмотрим на формулы (2) и (14), то мы увидим, что:
Замечательно, теперь из формулы (12) найдём спектр мощности:
Сигнал на выходе сумматора — фликкер-шум. Цвет этого шума — розовый (по мне, так он белый).
А теперь ответ на вопрос 90-летней давности:
Механизм возникновения фликкер-шума очень прост: если объект излучает гармонический сигнал произвольной частоты с мощностью P0, то множество таких объектов будет излучать сигнал со спектром фликкер-шума.
Истинный сигнал с равномерным спектром является фликкер-шумом. Любопытно, что же это за спектральная координата, относительно которой фликкер-шум выглядит равномерным.
Допустим, что генерируемые синусоиды различаются как по частоте, так и по мощности, тогда формула (16) запишется в следующем виде:
где P (f) — мощность реализации с частотой f.
Так как для процесса с равномерным спектром P (f) = P0, то P (f) удобно рассматривать как спектральную плотность мощности по некоторой величине Φ (Φ-СПМ):
По определению, спектральная плотность мощности должна иметь размерность мощности, делённой на размерность спектральной координаты. В данном случае Φ-СПМ имеет размерность мощности, следовательно, её спектральная координата Φ должна быть безразмерной. Таким образом, Φ-СПМ будет являться одновременно и спектральной плотностью мощности и зависимостью мощности генератора от частоты. Мощность в полосе частот df должна быть равна мощности в полосе dΦ:
Из формул (17), (18) и (19), получим:
и Φ определится по формуле:
Для исключения логарифмирования размерной величины, примем:
где f0 — некоторая частота, равная 1 Гц,
тогда:
Совершенно бессмысленную константу f0 мне пришлось ввести из-за того, что логарифмирование размерной величины у физиков вызывает fatal error.
А теперь мы можем представить фликкер-шум в виде суммы гармоник с одинаковыми амплитудами:
где An — амплитуда n-ой гармоники, Ф1 — Ф основной гармоники, φn — фаза n-ой гармоники.
Сделаем анимацию:
Можно ещё анимацию для одинаковых начальных фаз сделать:
Если объединим формулы (4), (17), (18), то получим красивое выражение:
Скажу ещё пару слов по квантовой механике.
Кроме спектральной плотности мощности существует ещё спектральная плотность энергии (СПЭ). Отличие их в том, что СПЭ используется для процессов с конечной энергией, а СПМ для процессов с бесконечной энергией. СПЭ характеризует энергию, приходящуюся на единицу полосы частот. А что нам мешает сделать тоже самое для процессов с конечной энергией? СПЭ по разным спектральным координатам будут связаны аналогичной формулой:
где Wf (f) — спектральная плотность энергии по частоте (f-СПЭ), WФ (Ф) — спектральная плотность энергии по Φ (Φ-СПЭ), WT (T) — спектральная плотность энергии по периоду (T-СПЭ).
Левая часть формулы (26) Вам ничего не напоминает? Эту формулу можно легко преобразовать в формулу для энергии кванта.
Давайте представим, что рассматриваемые выше генераторы выдают сигналы с произвольными частотами и произвольными мощностями, но энергия этих сигналов конечна. В природе подобные генераторы, мягко говоря, очень распространены — это электроны, а генерируемые ими сигналы — это кванты энергии.
Φ-СПЭ на конкретной частоте равна энергии:
Если принять f-СПЭ равной постоянной Планка, то формула (29) преобразуется в формулу для энергии кванта (28).
Так как постоянная Планка не зависит от частоты, то её можно рассматривать как равномерную f-СПЭ процесса, каждая реализация которого соответствует излучению электроном одного кванта энергии с произвольной частотой.
Если поделить f-СПЭ электромагнитной волны на постоянную Планка, то можно получить зависимость числа квантов волны от частоты. И так далее…
Вывод: фликкер-шум — сигнал с равномерным спектром, спектр которого искажается преобразованием Фурье.
Буду рад любой критике по статье.
