[Из песочницы] Задача о ранце в криптографии (Knapsack problem in cryptography)23.11.2020 00:32

Задача о рюкзаке (или Задача о ранце) в криптографии (англ. Knapsack problem) — это задача, на основе которой американские криптографы Ральф Меркл и Мартин Хеллман разработали первый алгоритм шифрования с открытым ключом.

Далее в программе

Формулировка задачи о рюкзаке (+почему рюкзак?)
Легкая и трудная проблемы
Примеры
История

Что такое шифрование с открытым ключом?

Для криптографии с открытым ключом требуется два ключа.

Один ключ сообщает вам, как зашифровать сообщение, и он является «общедоступным», поэтому любой может его использовать.

Другой ключ позволяет расшифровать сообщение. Этот код дешифрования хранится в секрете, поэтому только человек, знающий ключ, может расшифровать сообщение.

Некоторые алгоритмы имеют следующую характеристику: каждый из двух ключей может использоваться как для шифрования, так и для дешифрования.

Хотя это кажется малополезным, если вы пытаетесь сохранить что-то в секрете!

Первый общий алгоритм с открытым ключом использовал алгоритмом ранца.

Исходя из определения систем с открытым ключом, чтобы успешно шифровать (и расшифровать) сообщение нужны два ключа. «Легальный» получатель сообщения знает секретный ключ $inline$А$inline$, отправитель же владеет другим открытым ключом $inline$B$inline$.

Что делать, если злоумышленнику стал известен открытый ключ?

Есть ответ: открытый ключ должен получаться из секретного ключа при помощи преобразования ( односторонней функции) $inline$f$inline$, обладающего следующими двумя свойствами:

$inline$B = f (A)$inline$, зная A, вычислить саму функцию легко

$inline$A = f^{-1} (B)$inline$, а вычислить обратную функцию трудно

Что такое «легко» и «трудно»?

Алгоритмы с открытым ключом основаны на вычислительной сложности различных задач.
Более точно термин «легко» обычно означает, что проблему можно решить за полиномиальное время от длины входного сообщения. Т.е. пусть входное сообщение состоит из $inline$n$inline$ битов, тогда время вычисления — $inline$t \propto n^a$inline$, где $inline$a $inline$ — зафиксированная константа. Будем говорить, что алгоритм из класса полиномиальных алгоритмов Р.

Термин «трудно» более сложно определить. В общем случае можно считать, что невозможно решить проблему, если усилия для ее решения больше полиномиального времени от величины входного сообщения.

Т.е. пусть входное сообщение состоит из $inline$n$inline$ битов, и время вычисления функции $inline$t \propto 2n$inline$, то будем говорить, что это вычислительно невозможная задача.

Задача о рюкзаке формулируется так

Задан набор (рюкзачный вектор) $inline$A = (a_1, … , a_n) $inline$ — это упорядоченный набор из $inline$n$inline$ ($inline$n > 2), $inline$ различных натуральных чисел $inline$a_i$inline$. Пусть есть число $inline$k$inline$ — целое и положительное. Задачей является нахождение такого набора $inline$a_i$inline$, чтобы в сумме они давали ровно $inline$k$inline$.

В наиболее известном варианте задачи о рюкзаке требуется выяснить, обладает ли данная пара $inline$(A, k)$inline$ решением. В варианте, используемом в криптографии, нужно для данного входа $inline$(A, k)$inline$ построить решение, зная, что такое решение существует. Оба эти варианта являются NP-полными.

Аналогия с рюкзаком

В самом простом случае $inline$k$inline$ обозначает размер (вместительность) рюкзака, а каждое из чисел $inline$a_i$inline$ указывает размер (вес) предмета, который может быть упакован в рюкзак. Задачей является нахождение такого набора предметов, чтобы
рюкзак был полностью заполнен.

Т.е представьте, что у вас есть набор гирь 1, 6, 8, 15 и 24, вам нужно упаковать рюкзак весом 30.

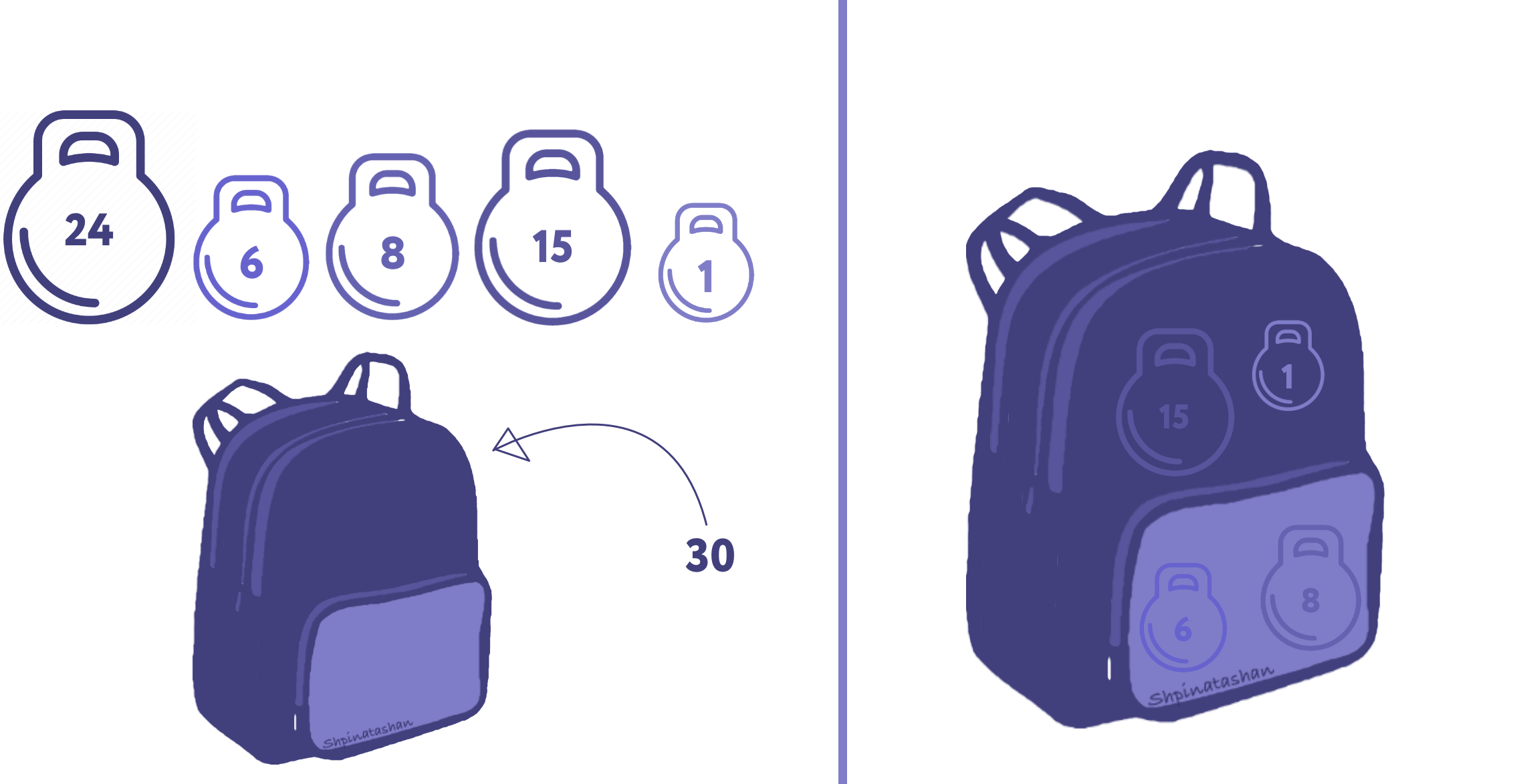
В принципе решение всегда может быть найдено полным перебором подмножеств $inline$А$inline$ и проверкой, какая из их сумм равна $inline$k$inline$. В нашем случае, это означает перебор $inline$2^5 = 32$inline$ подмножеств (включая при этом и пустое множество). Это вполне осуществимо.

Но что будет, если существует несколько сотен чисел $inline$a_i$inline$?
В нашем примере n = 5, чтобы не усложнять изложение. В реальных условиях пpимер будет иметь, скажем, 300 $inline$a_i-х$inline$. Суть здесь в том, что неизвестны алгоритмы, имеющие существенно меньшую сложность по сpавнению с полным перебором. Поиск среди $inline$2^{300}$inline$ подмножеств не поддается обработке. В самом деле, задача о рюкзаке известна как NP-полная… NP-полные задачи рассматриваются как трудновычислимые.

Подходит ли функция под указанные требования?

Определим функцию $inline$f (x)$inline$ следующим образом. Любое число $inline$0 ≤ x ≤ 2n − 1$inline$ может быть задано двоичным представлением из $inline$n$inline$ pазpядов, где пpи необходимости добавляются начальные нули. Теперь определим $inline$ f (x)$inline$ как число, получаемое из $inline$A$inline$ суммированием всех таких $inline$a_i$inline$, что соответствующий pазpяд в двоичном представлении $inline$x$inline$ равен 1.

Т.е.

$$display$$f (1) = f (0 . . . 001) = a_n$$display$$

$$display$$f (2) = f (0 . . . 010) = a_{n−1}$$display$$

$$display$$f (3) = f (0 . . . 011) = a_{n−1} + a_n$$display$$

$$display$$…$$display$$

Функция $inline$f (х)$inline$ определялась $inline$n-$inline$ набором $inline$ A$inline$. Очевидно, что если мы в состоянии вычислить $inline$x$inline$ из $inline$f (x)$inline$, то пpактически за то же время будет решена задача о рюкзаке: по $inline$x$inline$ немедленно вычисляется его двоичное представление, которое в свою очередь дает компоненты набора $inline$A$inline$, входящие в сумму для $inline$f (x)$inline$. С другой стороны, вычисление $inline$f (x)$inline$ из $inline$x$inline$ является легким. Так как задача о рюкзаке NP-полна, $inline$f (x)$inline$ является хорошим кандидатом для односторонней функции. Конечно, надо потребовать, чтобы $inline$n$inline$ было достаточно большим, скажем, не менее $inline$200$inline$.

Шифрование

Открытый текст

Открытый текст (англ. plain text) — в криптографии исходный текст, подлежащий шифрованию, либо получившийся в результате расшифровки. Может быть прочитан без дополнительной обработки (без расшифровки).

Шифровать можно двумя способами:

Шифр сообщения получается, если возвести элементы данного рюкзачного вектора в степень соответствующих им бит шифруемого сообщения и далее перемножить все результаты, то есть если $inline$A = (2,3,5)$inline$, а сообщение $inline$(100)$inline$, то шифром будет число $inline$2^1×3^0×5^0=2$inline$. Это мультипликативным способ.
Шифр сообщения получается, если умножить элементы данного рюкзачного вектора на соответствующие им биты шифруемого сообщения и далее просуммировать все результаты, то есть если $inline$A = (2,3,5)$inline$, а сообщение $inline$(100)$inline$, то шифром будет число $inline$2^ *1+3^ *0+5^ *0= 2$inline$. Такой способ называют аддитивным.

Пример

Для шифрования открытого текста в двоичном представлении его разбивают на блоки длины $inline$n$inline$ (например, Вы можете представить вес 30 двоичным кодом 11110). Считается, что единица указывает на наличие предмета в рюкзаке, а ноль на его отсутствие.

Шифрование рюкзака обеспечивает хороший подход к созданию открытых и закрытых ключей, где закрытый ключ прост в использовании, а открытый ключ трудно вычислить.
Так, мы можем составить систему, где:

открытым ключом будет служить «трудная» проблема, т.к. с помощью неё можно легко шифровать и невозможно дешифровать сообщение.

закрытым ключом — будет же служить «лёгкая» проблема, т.к. с помощью неё можно легко дешифровать сообщение. Без закрытого ключа придётся решать «трудную» задачу рюкзака.

«Лёгкая» проблема

Сверхрастущий рюкзачный вектор

Рюкзачный вектор $inline$A=(a_{1},…, a_{n})$inline$ называется сверхрастущим, если $inline$Σ_{i=1}^{j-1} a_{i} < a_{j}$inline$ для $inline$j=2,...,n$inline$, т.е каждый член последовательности больше суммы предыдущих.

Для сверхрастущих векторов Α задача о рюкзаке легко решаема. Т.е. рюкзак собрать несложно.
Рассмотрим на примере:

Алгоритм

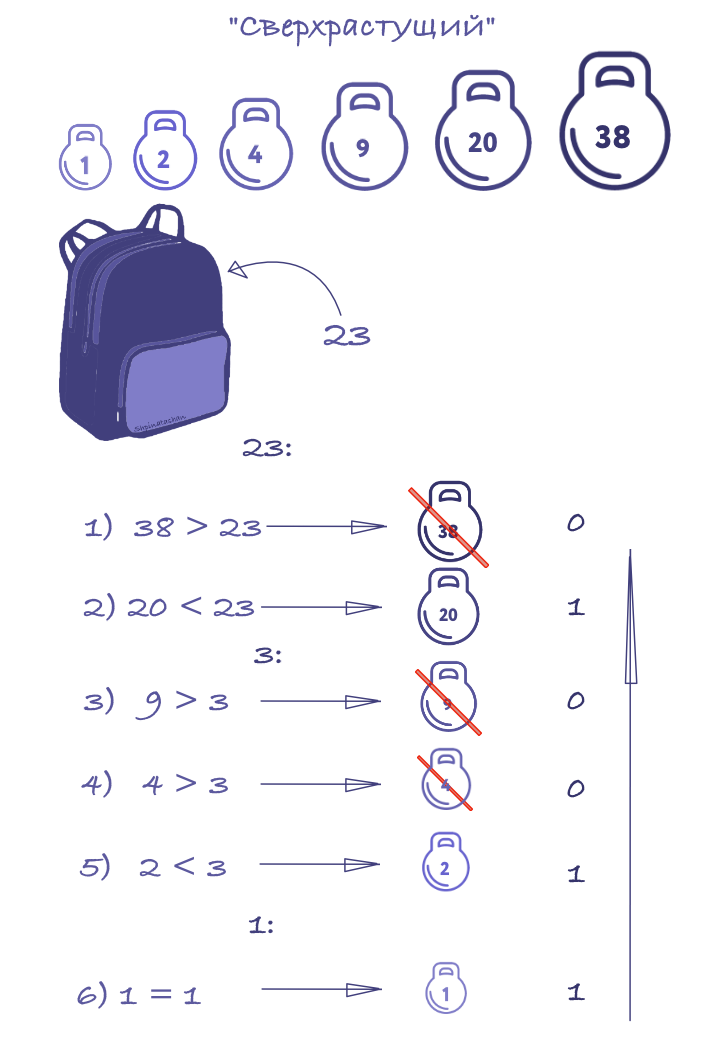
Общий вес ранца сравнить с наибольшим весом в последовательности.
Если общий вес меньше числа, значит, в рюкзаке его нет. Если общий вес больше числа, он в рюкзаке.
Вычесть число из общей суммы и сравните со следующим по величине числом.
Повторить (1)-(2) пока общая сумма не достигнет нуля.
Если сумма не достигает нуля, то решения нет.

«Трудная» проблема

Расшифровать задачу о несверхувеличивающемся рюкзаке гораздо сложнее.
Один алгоритм, который использует сверхувеличивающийся рюкзак для частного ключа и несверхувеличивающийся рюкзак для открытого ключа, был создан Мерклом и Хеллманом.
Они сделали это, взяв задачу сверхувеличивающегося рюкзака и преобразовав ее в несверхувеличивающую задачу.
(Меркл и Хеллман, используя модульную арифметику, разработали способ трансформации «лёгкого» рюкзака в «трудный»)

Создание открытого ключа

Несколько важных понятий

Если вышеуказанное условие $inline$m > max A$inline$ заменяется более сильным
условием $inline$m > Σ_{i=1}^{n} a_{i} $inline$, то говорят, что $inline$B$inline$ получается из $inline$A$inline$сильным модульным умножением относительно $inline$m, t$inline$.

Криптосистема — это завершённая комплексная модель, способная производить двусторонние криптопреобразования над данными произвольного объёма и подтверждать время отправки сообщения, обладающая механизмом преобразования паролей, ключей и системой транспортного кодирования.

Создатель криптосистемы выбирает такую систему $inline$A, t, m, B$inline$, что вектор $inline$A$inline$ является сверхрастущим, а $inline$B$inline$ получается из $inline$A$inline$ сильным модульным умножением относительно $inline$m, t$inline$. Вектор $inline$B$inline$ раскрывается как ключ зашифpования и двоичные блоки длины $inline$n$inline$ посылаются к проектировщику как числа $inline$β$inline$, полученные с помощью вектора $inline$B$inline$.

Перехватчик сообщений должен решать задачу о рюкзаке для входа $inline$(B, β)$inline$. Создатель же криптосистемы вычисляет $inline$α = (uβ, modm)$inline$
и решает задачу о рюкзаке для входа $inline$(A, α)$inline$. Почему все это работает,
показывает следующая лемма.

Лемма. Предположим, что $inline$A = (a_1, . . . , a_n) $inline$сверхрастущий вектор и вектор $inline$B$inline$ получен из $inline$ A$inline$ сильным модульным умножением относительно $inline$m, t$inline$. Предположим далее, что $inline$u ≡ t^{−1} (mod m)$inline$, $inline$β$inline$ —произвольное натуральное число и $inline$α = (uβ, modm)$inline$. Тогда справедливы следующие утверждения.

(i) Задача о рюкзаке $inline$(A, α)$inline$ разрешима за линейное время. Если решение существует, то оно единственно.
(ii) Задача о рюкзаке $inline$(B, β)$inline$ имеет не более одного решения.
(iii) Если существует решение для входа $inline$(B, β)$inline$, то оно совпадает с единственным решением для входа $inline$(A, α)$inline$.
доказательство (стр. 104)

Пример

Возмём сверхрастущую последовательность; например, {1, 2, 4, 10, 20, 40}. Модуль должен быть больше суммы всех чисел в последовательности, например 110. Множитель не должен иметь общих делителей с модулем. Итак, давайте выберем 31.

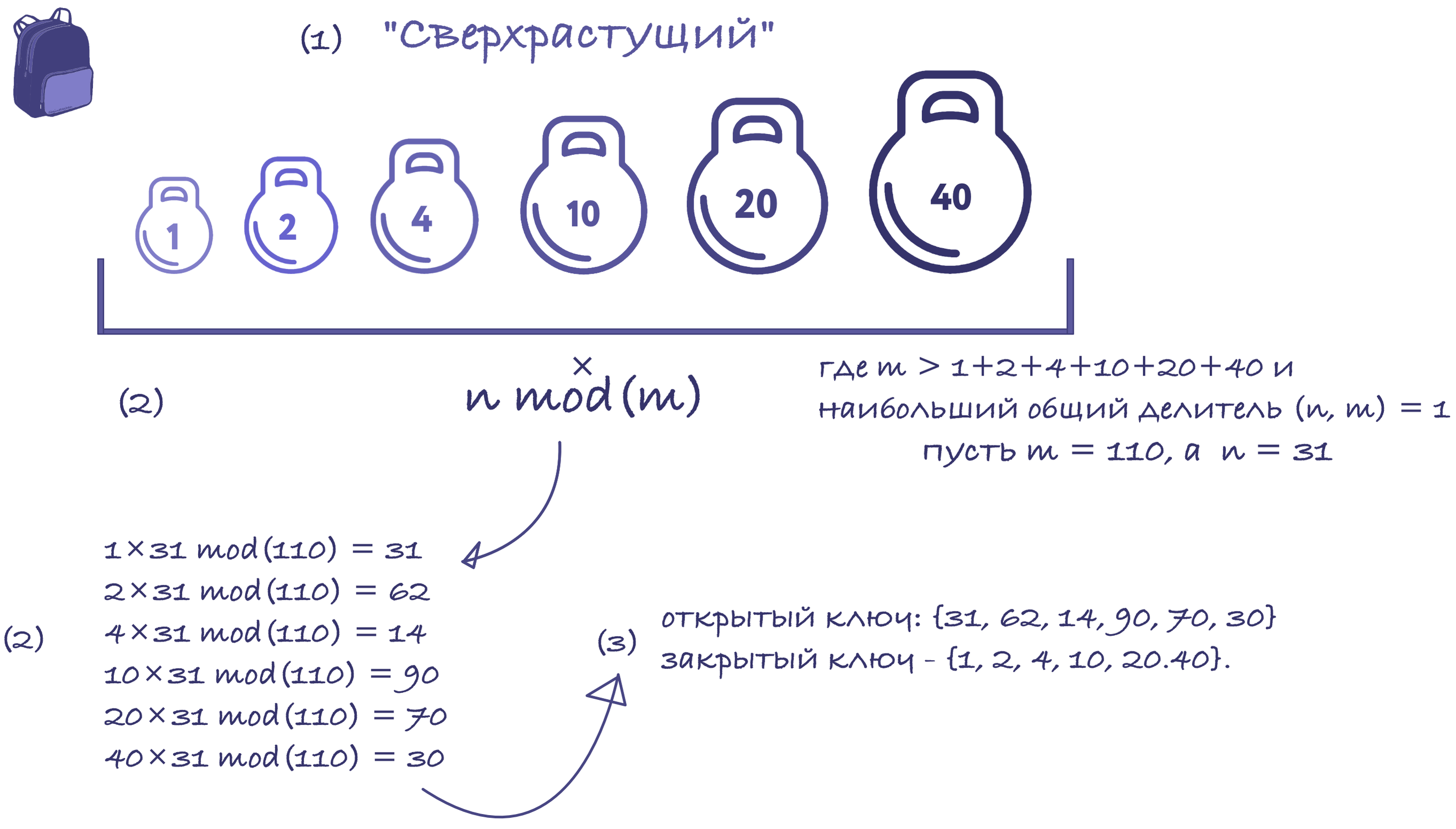
Итак, мы вычислили открытый ключ: {31, 62, 14, 90, 70, 30} и закрытый ключ — {1, 2, 4, 10, 20.40}.

Теперь попробуем отправить двоичную последовательность: 100100111100101110

Некоторые преимущества открытых ключей

При использовании криптосистемы с открытым ключом обе стороны не встречаются, они даже могут не знать друг друга и использовать любые виды связи.

Длина ключа. В симметричной криптографии, если ключ длиннее исходного сообщения, никакого действительного выигрыша не достигается. Что касается криптосистем с открытым ключом, то у них длина ключа зашифрования не имеет значения, поскольку он открытый и общедоступный. Поэтому и длина ключа расшифрования не так важна (получатель только хранит его в секретном месте)

История

Долгое время ранцевые криптосистемы рассматривались как наиболее привлекательные и перспективные криптосистемы благодаря их NP-полноте и высокой скорости шифрования и дешифрования. Многие схемы используют задачу о ранце (в различных вариациях), вот лишь несколько из них: the compact knapsack problem, the multiplicative knapsack problem, the modular knapsack problem, the matrixcover problem, the group factorization problem…

К сожалению, большинство из них уязвимы для атак. Оказалось, что нетривиально спроектировать защищенную криптосистему на основе задачи о ранце, хотя задача известна как NP-полная. Большинство ранцевых криптосистем было взломано. Несмотря на это, в отличие от целочисленной факторизации и дискретного логарифма, общая задача о рюкзаке (решении) является доказанной NP-полной проблемой.

Некоторые думают, что однажды может быть изобретен алгоритм с полиномиальным временем для решения задач целочисленной факторизации и дискретного логарифмирования, в то время как задача о рюкзаке по-прежнему останется NP-полной задачей.

Тут есть несколько «НО».

Во-первых, NP-полнота основана на анализе наихудшего случая, во-вторых, NP-полнота — это характеристики общей проблемы, а не конкретного случая. Это означает, что если рассматривать среднюю сложность, задача о рюкзаке может быть несложной.

Материал подготовлен на основе данной литературы:

(1) А. Саломаа. Криптография с открытым ключом/ Public-Key Cryptography. — Springer-Verlag, 1990. — Стр. 75–82, стр. 101—111

(2) Мин Кин Лай. Ранцевые криптосистемы: прошлое и будущее — Калифорнийский университет, 2001
(3) Baocang Wang, Qianhong Wu, Yupu Hu. A knapsack-based probabilistic encryption scheme. 2007

(4) — (5)