[Из песочницы] Введение в машинное обучение с tensorflow
Если мы в ближайшие пять лет построим машину с интеллектуальными возможностями одного человека, то ее преемник уже будет разумнее всего человечества вместе взятого. Через одно-два поколения они попросту перестанут обращать на нас внимание. Точно так же, как вы не обращаете внимания на муравьев у себя во дворе. Вы не уничтожаете их, но и не приручаете, они практически никак не влияют на вашу повседневную жизнь, но они там есть.
Сет Шостак
Введение.
Серия моих статей является расширенной версией того, что я хотел увидеть когда только решил познакомиться с нейронными сетями. Он рассчитан в первую очередь на программистов, желающих познакомится с tensorflow и нейронными сетями. Уж не знаю к счастью или к сожалению, но эта тема настолько обширна, что даже мало-мальски информативное описание требует большого объёма текста. Поэтому, я решил разделить повествование на 4 части:
- Введение, знакомство с tensorflow и базовыми алгоритмами (эта статья)
- Первые нейронные сети
- Свёрточные нейронные сети
- Рекуррентные нейронные сети
Изложенная ниже первая часть нацелена на то, чтобы объяснить азы работы с tensorflow и попутно рассказать, как машинное обучение работает впринципе, на примере tensorfolw. Во второй части мы наконец начнём проектировать и обучать нейронные сети, в т.ч. многослойные и обратим внимание на некоторые нюансы подготовки обучающих данных и выбора гиперпараметров. Поскольку свёрточные сети сейчас пользуются очень большой популярность, то третья часть выделена для подробного объяснения их работы. Ну, и в заключительной части планируется рассказ о рекуррентных моделях, на мой взгляд, — это самая сложная и интересная тема.
Установка tensorflow
Хотя описание процесса установки tensorflow и не является целью статьи, я вкратце опишу процесс установки cpu-версии для 64-разрядных windows систем и дополнений, используемых далее в тексте. В общем случае процедуру установки можно посмотреть на сайте tensorflow.
- Скачиваем и устанавливаем python версии 3.5.* (последняя версия на момент написания 3.5.3). В процессе установки установите галочку в пункте «Add Python 3.5 to PATH». Если же вы не хотите добавлять директории этой версию python в переменные окружения, например из-за активного использования другой версии интерпретатора, то дальнейшие шаги вы должны выполнять из папки Scripts, указанной версии дистрибутива (cd «путь к python 3.5/Scripts»).
- После установки запустите командную строку (именно после установки, иначе директории python не попадут в переменную среды PATH).
- Далее выполните команды:
- обновление pip: «pip install --upgrade pip»
- обновление setuptools: «pip install -U pip setuptools»
- устнановка tensorflow 1.0.1 под CPU: «pip install --ignore-installed --upgrade ci.tensorflow.org/view/Nightly/job/nightly-win/DEVICE=cpu, OS=windows/lastSuccessfulBuild/artifact/cmake_build/tf_python/dist/tensorflow-1.0.1-cp35-cp35m-win_amd64.whl»
- установка matplotlib (для графиков): «pip install matplotlib»
- установка Jupyter: «pip install jupyter»
- Установка завершена, для запуска Jupyter выполните команду «jupyter notebook» и в открывшейся вкладке можете открыть ipynb версию статьи (брать тут).
Ниже приведён скрипт на vbs, если вы просто хотите быстро установить весь нужный софт, не вдаваясь в детали, то просто запустите его и следуйте инструкциям:
'получаем версию питона по-умолчанию
Function GetPythonVersion()
On Error Resume Next
Err.Clear
GetPythonVersion = vbNullString
Set WshShell = CreateObject("WScript.Shell")
Set WshExec = WshShell.Exec("python --version")
If Err.Number = 0 Then ' если питон вообще есть
Set TextStream = WshExec.StdOut
Str = vbNullString
While Not TextStream.AtEndOfStream
Str = Str & Trim(TextStream.ReadLine()) & vbCrLf
Wend
Set objRegExp = CreateObject("VBScript.RegExp")
objRegExp.Pattern = "(\d+\.?)+"
objRegExp.Global = True
Set objMatches = objRegExp.Execute(Str)
PythonVersion = "0"
For i=0 To objMatches.Count-1 ' должно быть только одно совпадение
PythonVersion = objMatches.Item(i).Value
Next
GetPythonVersion = PythonVersion
Else
Err.Clear
End If
End Function
Function DownloadPython()
Err.Clear
Set x = CreateObject("WinHttp.WinHttpRequest.5.1")
call x.Open("GET", "https://www.python.org/ftp/python/3.5.3/python-3.5.3-amd64-webinstall.exe", 0)
x.Send()
Set s = CreateObject("ADODB.Stream")
s.Mode = 3
s.Type = 1
s.Open()
s.Write(x.responseBody)
call s.SaveToFile("python-3.5.3-amd64-webinstall.exe", 2)
DownloadPython = "python-3.5.3-amd64-webinstall.exe"
End Function
Function InstallPython()
InstallPython = False
PythonVersion = GetPythonVersion()
If Mid(PythonVersion, 1, 3)="3.5" Then
InstallPython = True
Else
txt = vbNullString
If Len(PythonVersion) > 0 Then
txt = "Обнаружена не подходящая версия питона"
Else
txt = "Питон не установлен"
End If
If MsgBox(txt & vbCrLf & "Скачать подходящую версию?", 4) = 6 Then
MsgBox("Не забудьте поставить галочку в пункте 'Add Python 3.5 to PATH'")
Set WshShell = WScript.CreateObject("WScript.Shell")
WshShell.Run DownloadPython(), 0, True
MsgBox("установка питона завершена, запустите скрипт повторно для продолжения установки")
End If
End If
End Function
If InstallPython() Then
Set WshShell = WScript.CreateObject("WScript.Shell")
'установка tensorflow
WshShell.Run "pip install --upgrade pip", 1, True
WshShell.Run "pip install --ignore-installed --upgrade https://ci.tensorflow.org/view/Nightly/job/nightly-win/DEVICE=cpu,OS=windows/lastSuccessfulBuild/artifact/cmake_build/tf_python/dist/tensorflow-1.0.1-cp35-cp35m-win_amd64.whl", 1, True
WshShell.Run "pip install -U pip setuptools", 1, True
WshShell.Run "pip install matplotlib" , 1, True
WshShell.Run "pip install jupyter" , 1, True
If MsgBox("Всё готово, запустить Jupyter notebook?", 4) = 6 Then
WshShell.Run "jupyter notebook" , 1, False
End If
End IfЗнакомство с tensorflow
Принципы работы с tensorflow достаточно просты. Мы должны составить граф операций, затем передать в этот граф данные и дать команду произвести вычисления. На картинке ниже вы можете увидеть 3 примера таких графов:
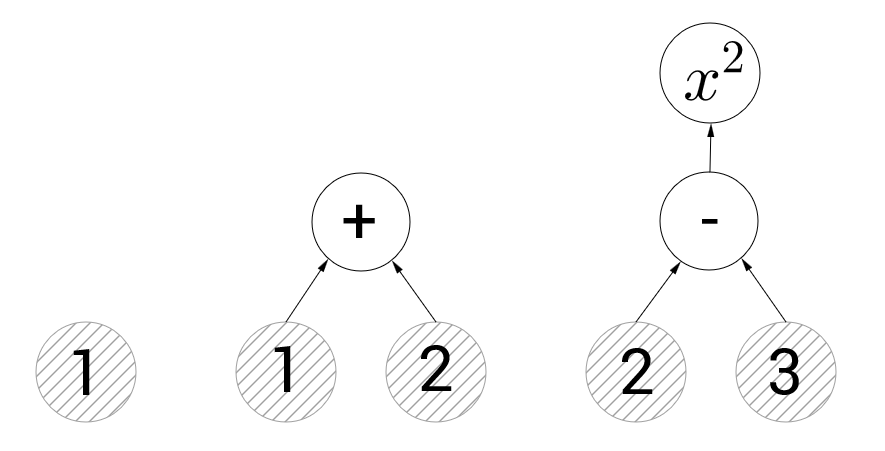
Граф слева содержит только одну вершину, представляющую константу со значением 1. Здесь и далее по тексту, в таких иллюстрациях, кругами с серой штриховкой будут обозначаться вершины с константами, а без штриховки вершины с операциями. Центральный граф иллюстрирует операцию сложения. Если мы попросим tensorflow вычислить значение вершины, представляющей операцию сложения, то он вычислит значения направленных в него рёбер графа и просуммирует их (т.е. будет возвращено 3). На правом же графе у нас две вершины с операциями — вычитание и возведение в квадрат. Если мы попытаемся вычислить вершину, представляющую возведение в квадрат, то tensorflow сперва выполнит вычитание. Я думаю концепция графов вычислений ни у кого затруднений не вызовет.
Пустой граф можно создать функцией tf.Graph (), кроме того граф по-умолчанию создаётся при подключении библиотеки и если вы не будете явно указывать граф, то будет использоваться именно он. В примере ниже показано, как можно создать две константы в двух разных графах.
import tensorflow as tf # в дальнейшем эта строка будет опускаться
# сохраняем граф по-умолчанию в переменную
default_graph = tf.get_default_graph()
# объявляем константу в графе по-умолчанию
c1 = tf.constant(1.0)
# создаём пустой граф
second_graph = tf.Graph()
with second_graph.as_default():
# в этом блоке мы работаем во втором графе
c2 = tf.constant(101.0)
print(c2.graph is second_graph, c1.graph is second_graph) # True, False
print(c2.graph is default_graph, c1.graph is default_graph) # False, TrueПередача данных и выполнение операций происходят в сессиях. Запуск сессии осуществляется вызовом tf.Session, а её закрытие вызовом метода close на объекте сессии. Можно использовать конструкцию with, которая автоматический закрывает сессию:
default_graph = tf.get_default_graph()
c1 = tf.constant(1.0)
second_graph = tf.Graph()
with second_graph.as_default():
c2 = tf.constant(101.0)
session = tf.Session() # открываем сессию на графе по-умолчанию
print(c1.eval(session=session))
# print(c2.eval(session=session)) # так нельзя, не тот граф
session.close()
# тоже самое:
with tf.Session() as session:
print(c1.eval()) # не нужно передавать сессию в метод eval
# используем другой граф:
with tf.Session(graph=second_graph) as session:
print(c2.eval()) # не нужно передавать сессию в метод eval
#Вывод:
# 1.0
# 1.0
# 101.0Надеюсь про графы и сессии в общих чертах ясно, подробно их функционал тут разбираться не будет, тем кто хочет досконально разобрать эти механизмы стоит ознакомится непосредственно с документацией. А далее мы переходим к построению графов. В предыдущих примерах в граф добавлялись константы и настало время узнать что это такое и чем они отличаются от placeholder’ов и переменных. В примере ниже построен более сложный граф, представляющий выражение $inline$a\cdot x+b$inline$.
# объявляем константу a. Это константа и её значение будет зашито в самом графе
# в объявлении ниже указаны все возможные параметры, хотя достаточно было указать только значение:
# a = tf.constant(2.0)
# описание параметров:
# value (первый аргумент) - значение константы
# shape - размерность. Например: [] - число, [5] - массив из 5 элементов, [2, 3] - матрица 2x3(2 строки на 3 столбца)
# dtype - используемый тип данных, список возможных значений тут https://www.tensorflow.org/api_docs/python/tf/DType
# name - имя узла. Позволяет дать узлу имя и в дальнейшем находить узел по нему
a = tf.constant(2.0, shape=[], dtype=tf.float32, name="a")
# объявляем переменную x
# при объявлении переменной можно указать достаточно много аргументов
# на полный список можно взглянуть в документации, скажу только про основные:
# initial_value - значение переменной после инициализации
# dtype - тип, name - имя, как и у констант
x = tf.Variable(initial_value=3.0, dtype=tf.float32)
# поскольку обычно нам нужно передавать в модель данные по ходу работы, константы нам не очень подходят
# для входных данных предусмотрен специальный тип placeholder
# в отличии от константы он не требует указать значение заранее, но требует указать тип
# также можно указать размерность и имя
b = tf.placeholder(tf.float32, shape=[])
# и объявляем саму операцию умножения, при желании можно так же указать имя
f = tf.add(tf.multiply(a, x), b) # можно было написать просто f = a*x + b
with tf.Session() as session:
# прежде всего нужно инициализировать все глобальные переменные
# в нашем случае это только x
tf.global_variables_initializer().run()
# просим вычислить значение узла f внутри сессии
# в параметре feed_dict передаём значения всех placeholder'ов
# в данном случае b = -5
# функция вернёт список значений всех узлов, переданных на выполнение
result_f, result_a, result_x, result_b = session.run([f, a, x, b], feed_dict={b: -5})
print("f = %.1f * %.1f + %.1f = %.1f" % (result_a, result_x, result_b, result_f))
print("a = %.1f" % a.eval()) # пока сессия открыта, можно вычислять узлы
# метод eval похож на метод run у сессии, но не позволяет передать входные данные (параметр feed_dict)
# переменные можно модифицировать во время выполнения, не трогая граф:
x = x.assign_add(1.0)
print("x = %.1f" % x.eval())
# Вывод:
# f = 2.0 * 3.0 + -5.0 = 1.0
# a = 2.0
# x = 4.0Итак, placeholder — это узел, через который в модель будут передаваться новые данные, а переменная (Variable) — это узел, который может изменяться по ходу выполнения графа. Я надеюсь, что вышеописанный материал всем понятен, т.к. его как раз достаточно для того, чтобы приступить к обучению первой модели. В предыдущем фрагменте кода мы составили граф линейной функции $inline$a\cdot x+b$inline$, теперь же давайте пойдём немного дальше и аппроксимируем функцию $inline$a\cdot x+b$inline$ по набору точек. Да, я знаю, что всех уже задолбала эта задача, как и распознование символов и ещё ряд клишейных примеров, но смиритесь, вам предстоит пройти через всех них…
Первый обучающий алгоритм
Чтобы tensorflow мог обучать модель нам нужно добавить ещё 2 вещи: функцию потерь и сам алгоритм оптимизации.
Функция потерь — это функция, которая принимает значение функции предсказанное моделью и фактическое значение, а возвращает расстояние между ними (будем называть это значение ошибкой). Например, если мы предсказываем вещественное значение, то в качестве функции потерь можно взять квадрат разности аргументов или модуль их разности. Если у нас задача классификации, то функция потерь может возвращать 0 при правильном ответе и 1 при ошибках. Грубо говоря, функция потерь должна вернуть неотрицательное вещественное число и оно должно быть тем больше, чем сильнее модель ошибается и тогда задача обучения модели сведётся к минимизации. И хотя последнее предложение не совсем корректно, зато в полной мере отражает идею машинного обучения.
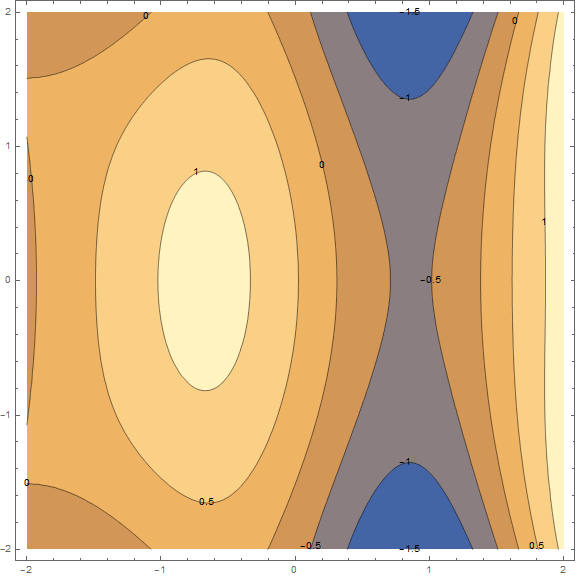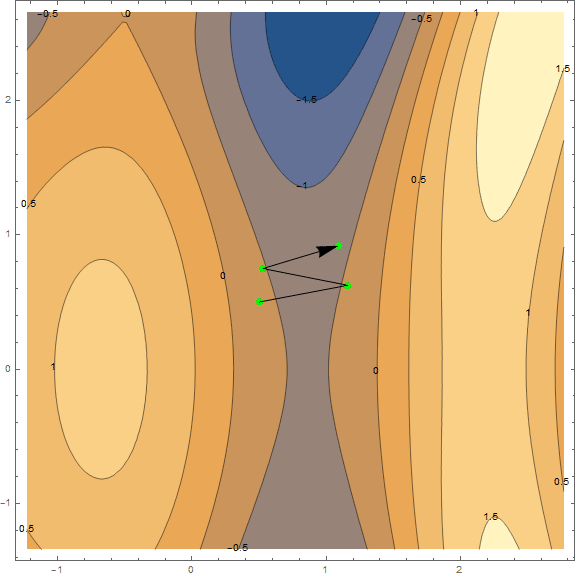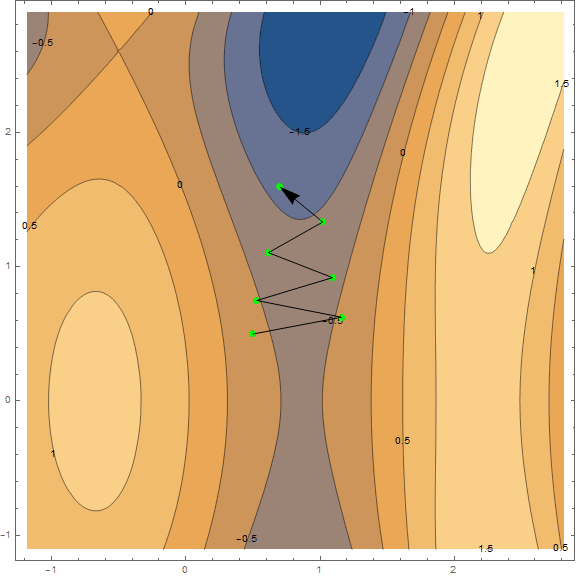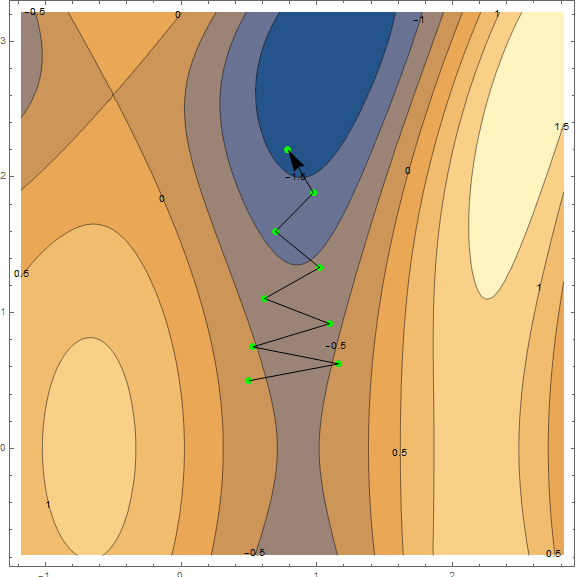
Из методов оптимизации мы рассмотрим только классический градиентный спуск. Про него написано уже очень много, поэтому я не буду разбирать его «по кирпичику» и вдаваться в детали (материал и так выходит не маленький). Однако его нужно понимать, поэтому постараюсь коротко и наглядно объяснить метод при помощи визуализаций. Ниже представлены 2 варианта одного и того же графика — $inline$\sin\left (\frac12x^2-\frac14y^2\right)+\cos (2x+1)$inline$. Задача метода — найти локальный минимум, т.е. из точки (взятой наугад, на графике $inline$\left (\frac12;\frac12\right)$inline$) попасть в углубление (синяя зона на графиках).
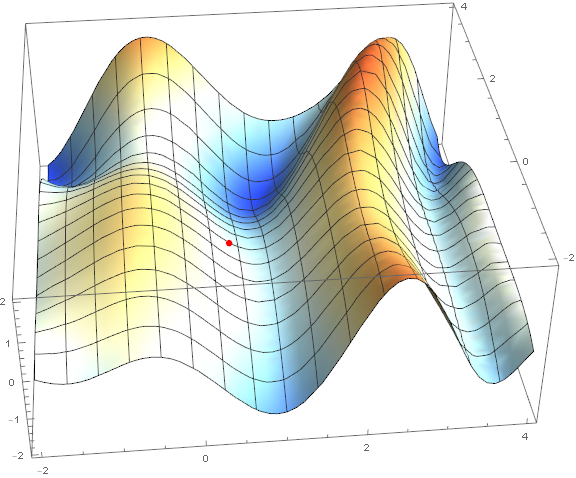
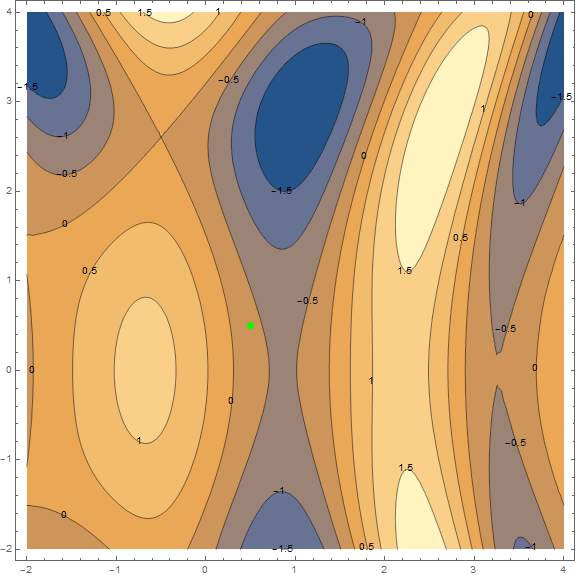
Суть метода в том, чтобы идти в направлении противоположном градиенту функции в текущей точке. Градиент — это вектор, который указывает в направлении наибольшего роста функции. Математически это вектор из производных по всем аргументам — $inline$\mathrm{grad}(f)=\nabla f = \left (\frac{\partial f}{\partial x},\;\frac{\partial f}{\partial y}\right)$inline$. Функция взята наугад и вычисления на ней мы проводить не станем, для практики у нас есть более простой пример, для начала посмотрите на визуализацию нескольких шагов алгоритма:
Отдельно стоит сказать о скорости с которой нужно двигаться к минимуму (применительно к задаче машинного обучения, это будет называться скоростью обучения). Для получения первых результатов, нам достаточно будет подобрать фиксированную скорость. Однако часто бывает хорошей идеей понижать её по ходу выполнения алгоритма, т.е. двигаться всё меньшими и меньшими шажками. Пока этого достаточно, более подробно будем разбирать метод с практикой, по мере необходимости.
В следующем примере мы попытаемся восстановить значение функции $inline$2x-3$inline$ на интервале от -2 до 2 по 50-ти точками с нормально распределённым шумом. Обучать модель мы будем наборами (пакетами) по 5 точек при помощи стохастического градиентного спуска (англ. SGD — Stochastic Gradient Descent). Давайте сразу перейдём к коду.
import numpy as np
import tensorflow as tf
%matplotlib inline
import matplotlib.pyplot as plt
samples = 50 # количество точек
packetSize = 5 # размер пакета
def f(x): return 2*x-3 # искомая функция
x_0 = -2 # начало интервала
x_l = 2 # конец интервала
sigma = 0.5 # среднеквадратическое отклонение шума
np.random.seed(0) # делаем случайность предсказуемой (чтобы все желающие могли повторить вычисления на этом же наборе данных)
data_x = np.arange(x_0,x_l,(x_l-x_0)/samples) # массив [-2, -1.92, -1.84, ..., 1.92, 2]
np.random.shuffle(data_x) # перемешать, но не взбалтывать
data_y = list(map(f, data_x)) + np.random.normal(0, sigma, samples) # массив значений функции с шумом
print(",".join(list(map(str,data_x[:packetSize])))) # первый пакет иксов
print(",".join(list(map(str,data_y[:packetSize])))) # и первый пакет игреков
tf_data_x = tf.placeholder(tf.float32, shape=(packetSize,)) # узел на который будем подавать аргументы функции
tf_data_y = tf.placeholder(tf.float32, shape=(packetSize,)) # узел на который будем подавать значения функции
weight = tf.Variable(initial_value=0.1, dtype=tf.float32, name="a")
bias = tf.Variable(initial_value=0.0, dtype=tf.float32, name="b")
model = tf.add(tf.multiply(tf_data_x, weight), bias)
loss = tf.reduce_mean(tf.square(model-tf_data_y)) # функция потерь, о ней ниже
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss) # метод оптимизации, о нём тоже ниже
with tf.Session() as session:
tf.global_variables_initializer().run()
for i in range(samples//packetSize):
feed_dict={tf_data_x: data_x[i*packetSize:(i+1)*packetSize], tf_data_y: data_y[i*packetSize:(i+1)*packetSize]}
_, l = session.run([optimizer, loss], feed_dict=feed_dict) # запускаем оптимизатор и вычисляем "потери"
print("ошибка: %f" % (l, ))
print("a = %f, b = %f" % (weight.eval(), bias.eval()))
plt.plot(data_x, list(map(lambda x: weight.eval()*x+bias.eval(), data_x)), data_x, data_y, 'ro')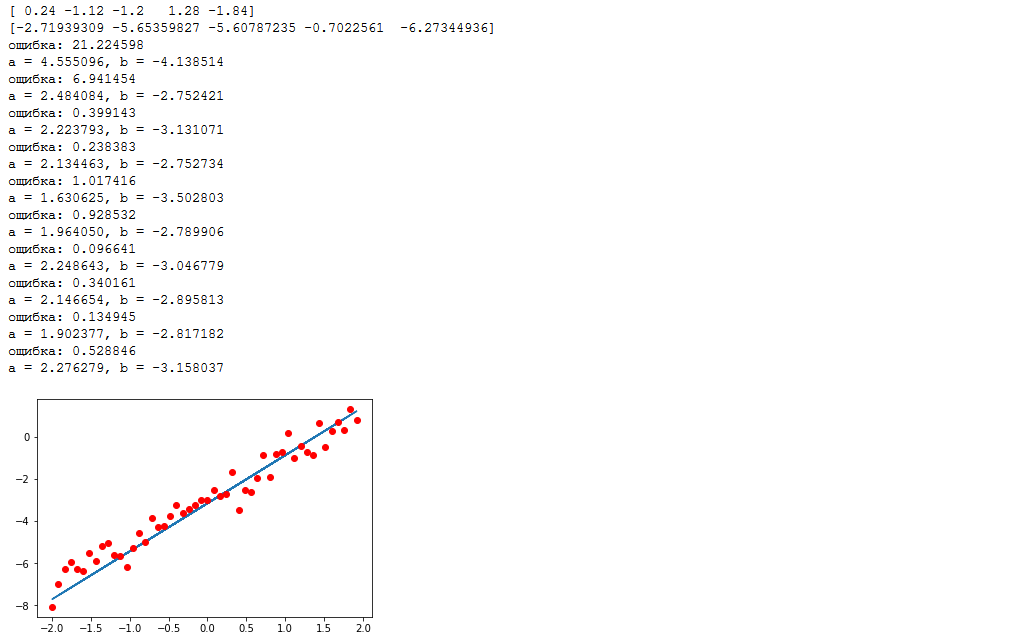
Наш граф выглядит примерно так:
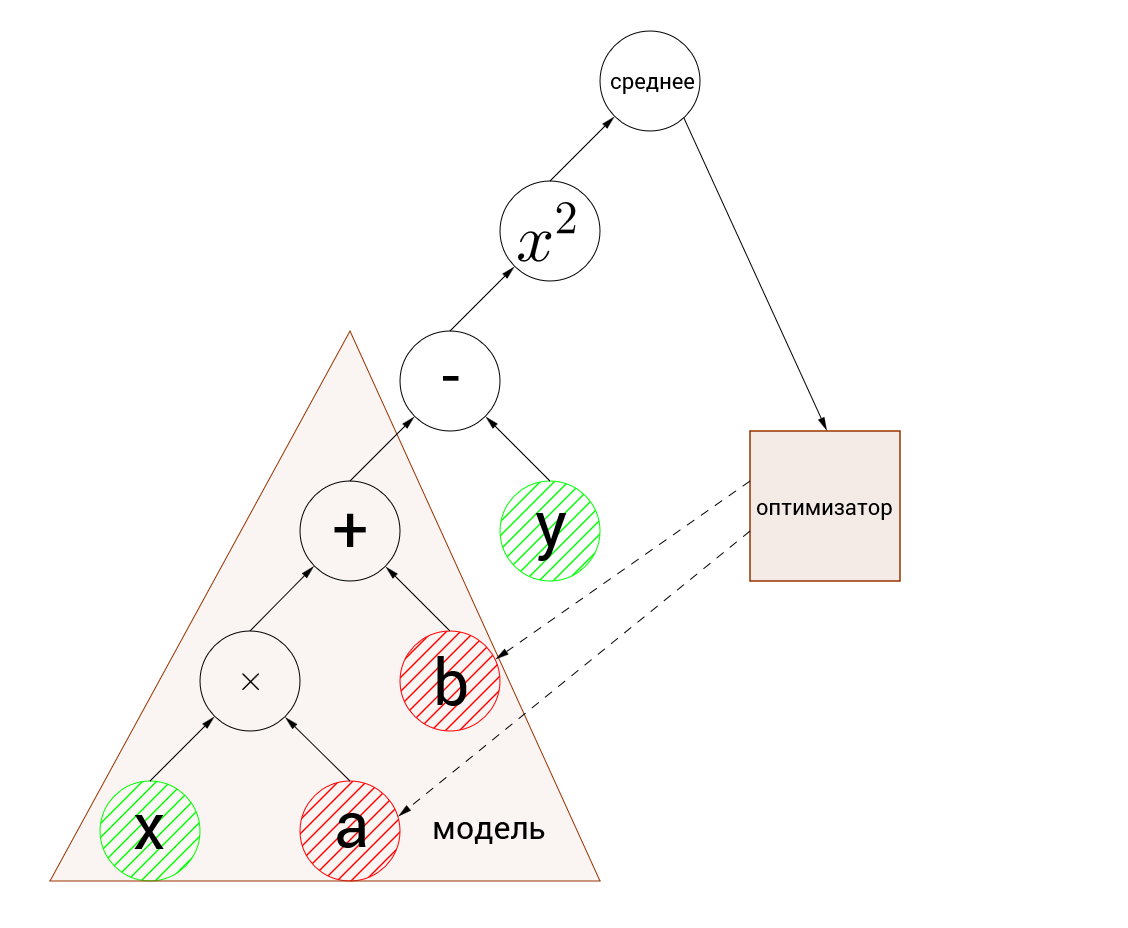
зелёным выделены входные узлы, а красным оптимизируемые переменные.
Первое, что должно броситься в глаза, это несовпадение размерностей у входных узлов с переменными. Входные узлы принимают массивы по 5 элементов, а переменные являются числами. Это называется пакетными вычислениями (broadcasting). Грубо говоря, когда нужно произвести вычисления над массивами, один из которых имеет лишнее измерение, вычисления производятся отдельно для каждого элемента бОльшего массива и результатом будет массив бОльшей размерности. Т.е. [1,2,3,4,5] + 1 = [2,3,4,5,6], это довольно сложно сформулировать, но должно быть интуитивно понятно.
Давайте вручную пересчитаем действия алгоритма, я думаю это лучший способ понять что происходит. Итак, на входы передаются аргументы — [ 0.24, -1.12, -1.2, 1.28, -1.84] и значения [-2.72, -5.65, -5.61, -0.70, -6.27] (округлено до сотых). Сперва мы пакетно вычисляем значение функции, напомню, что после инициализации переменных функция выглядит как $inline$0.1\cdot x + 0$inline$. Подставляем каждый аргумент:
$$display$$\left[\begin{matrix}0.1\cdot 0.24+0=0.024\\ 0.1\cdot -1.12+0=-0.112\\ 0.1\cdot -1.2+0=-0.12\\ 0.1\cdot 1.28+0=0.128\\ 0.1\cdot -1.84+0=-0.184\end{matrix}\right.$$display$$
далее полученные значения вычитаются из эталонных, возводятся в квадрат и вычисляется среднее значение:
$$display$$\left[\begin{matrix}(0.024-(-2.72))^2\approx7.53\\ (-0.112-(-5.65))^2\approx30.67\\(-0.12-(-5.61))^2\approx30.14\\ (0.128–0.7)^2\approx0.69\\(-0.184-(-6.27))^2\approx37.04\end{matrix}\right.\Rightarrow\frac{7.53+30.67+30.14+0.69+37.04}5\approx21.21$$display$$
отличие примерно в сотую от выведенного в лог значения вызвана округлением до сотых во время расчётов. Итак, ошибку мы посчитали, теперь пришло время разобраться с оптимизацией. На изображении графа выше, пунктирными стрелками, показано что оптимизатор изменяет переменные. У вас уже должно быть интуитивное понимание того, как работает градиентный спуск. В этом примере используется стохастический градиентный спуск со скоростью 0.5. Давайте по порядку, мы оптимизируем переменные a и b, так что по ним и находим градиент:
$$display$$f=(a\cdot x + b — y)^2\Rightarrow \left\{\begin{matrix}\frac{\partial f}{\partial a}=2x (ax+b-y)\\\frac{\partial f}{\partial b}=2(ax+b-y)\end{matrix}\right.$$display$$
Нам нужно улучшить значение по всему набору точек, поэтому вычисляем среднее значение градиента, для удобства по каждой переменной отдельно:
$$display$$\begin{matrix}a\Rightarrow\frac{1.31712+(-12.4051)+(-13.176)+2.11968+(-22.3965)}{5}=-8.90816\\b\Rightarrow\frac{5.488+11.076+10.98+1.656+12.172}{5}=8.2744\end{matrix}$$display$$
Ну и, наконец, меняем значения оптимизируемых переменных с учётом заданной скорости:
$$display$$\begin{matrix}a_{new}=a_{old}-0.5\cdot-8.90816=0.1–0.5\cdot (-8.90816)=4.55\\b_{new}=b_{old}-0.5\cdot8.2744=0–0.5\cdot (-8.90816)=-4.14\end{matrix}$$display$$
Значения $inline$a_{new}$inline$ и $inline$b_{new}$inline$ и есть искомые значения переменных. Эти вычисления повторяются в цикле на каждом наборе точек. Почему такой метод называется стохастическим? Потому что мы вычисляем градиент только на небольшом фрагменте данных (пакете), а не на всех точках сразу. Таким образом стохастический спуск требует гораздо меньше вычислений, но не гарантирует уменьшение ошибки на каждой итерации. Как ни странно этот «шум» в величине сходимости по времени может оказаться даже полезен, т.к. позволяет «выкорабкиваться» из локальных минимумов.
Собственно, на этом пока можно закончить. Статья получилась даже относительно небольшой, что не может не радовать. Я впервые пишу такого рода материал, так что если вы считаете, что в статье недостаточно подробно или в неверном ключе рассмотренны какие-то моменты, то, пожалуйста, напишите об этом — статья обязательно будет дополнена и скорректирована на основе конструктивной критики. Кроме того это поможет лучше подготовить к публикации последующие части, которые обязательно будут тут выложены (разумеется за исключением сценария при котором статья будет встречена негативно).
В заключение очень хотелось бы поблагодарить своего друга Николая Саганенико, за помощь в подготовке материала. Именно благодаря ему моя небольшая шпаргалка для личного пользования превратилась в вышеизложенный поток сознания.
