[Из песочницы] Трактат об энтропии
Приветствую тебя, читатель Гиктаймс!
Многие слышали о такой загадочной штуке, как энтропия. Обычно её называют мерой хаоса, мерой неопределённости и ещё прибавляют, что она непременно растёт. Я с огромной болью переношу употребление имени Энтропии всуе и решил, наконец, написать ликбез по этому вопросу.
Второе начало
Что будет, если бросить футбольный мяч на землю? Очевидно, он несколько раз подпрыгнет, причём каждый следующий раз на всё меньшую высоту, а затем и вовсе упокоится на земле. А что будет, если в горячий чай опустить металлическую ложку? Ложка нагреется, чай остынет. Ничего сложного, не так ли? В каждом из этих примеров направление протекания процессов кажется очевидным: мяч не может подпрыгивать выше и выше и даже не может вечно подпрыгивать до одной высоты, а чай не может ещё больше охладить ложку. Из таких житейских очевидностей были выведены два постулата (равноценных), каждый из которых может в равной степени называться вторым началом термодинамики:
— единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретого тела к более нагретому (постулат Клаузиуса);
— теплота наиболее холодного из участвующих в процессе тел не может служить источником работы (постулат Томсона), т.е. единственным результатом любой совокупности процессов не может быть превращение теплоты в работу.
Не зря эти два утверждения названы постулатами, они аксиоматичны, доказать их нельзя, они лишь подтверждаются своими следствиями и всем человеческим опытом.
Вроде всё и ясно: горячие тела остывают, холодные нагреваются, энергия рассеивается. Но как насчёт ещё одной задачки? Смешали по 1 моль водорода, азота и аммиака при температуре 500 oС в реакторе объёмом 10 литров в присутствии катализатора:

В какую сторону пойдёт реакция: образования аммиака или его разложения? Ммм… Кажется, нам нужно больше уравнений.
Цикл дедушки Карно
Знает каждый инженер в равно омега эр КПД большего, чем в цикле Карно, достичь невозможно.
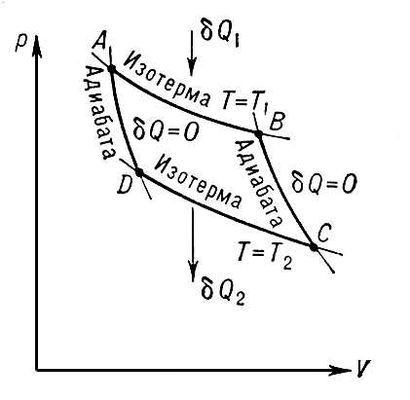
Цикл состоит из двух изотерм и двух адиабат. Его КПД равен:

где Qн и Qх — количество теплоты, полученное от нагревателя и отданное холодильнику соответственно, Tн и Tх — температуры нагревателя и холодильника.
Так почему же КПД цикла Карно максимален, почему нельзя придумать ничего эффективнее? По определению, КПД есть отношение полезной работы к затраченной. Цикл состоит из двух изотерм и двух адиабат. С изотермами всё просто: так как внутренняя энергия системы в ходе изотермического процесса не изменяется, вся теплота, полученная из внешней среды, идёт на совершение работы, т.е. КПД этого конкретного процесса 100%. Изотермы две: одна для расширения рабочего тела (в ходе этого процесса полезная работа совершается), а вторая для возвращения к исходному состоянию (в ходе этого процесса рабочее тело сжимается). Очевидно, что нет никакого смысла проводить оба этих процесса при одной и той же температуре, т.к. тогда вся энергия, полученная от нагревателя и затраченная на совершение полезной работы, пойдет на обратный процесс — сжатие. Сжимать опять же лучше по изотерме, потому что в этом случае тепло, отдаваемое холодильнику, уменьшает только объём системы, но не изменяет внутреннюю энергию, т.е. для достижения той же степени сжатия потребуется отдать меньшее количество теплоты, а эта теплота не идёт на совершение работы (и вообще отрицательна), т.е. уменьшает КПД. Для соединения двух изотерм используются две адиабаты. В ходе адиабатического процесса теплообмен с окружающей средой отсутствует, система тепла не получает, соответственно, КПД не уменьшается (увеличится он не может в силу того, что процесс-переводчик от одной изотермы к другой повторяется дважды за цикл, но в разных направлениях: вся работа, что совершается в прямом направлении, затратится в обратном).
Таким образом, полученная от нагревателя теплота расходуется на совершение работы, а затем часть работы расходуется на сжатие рабочего тела вновь по изотерме (работу в ходе адиабатных процессов оставим за скобками, она идёт за счёт внутренней энергии рабочего тела и мирно взаимоуничтожается). Чем меньше вторая величина, тем больше КПД.
А теперь приступим к мысленной гимнастике. Пусть у нас будут две тепловые машины с разными рабочими телами, работающие по циклу Карно. Причём первая работает равновесно (т.е., в любой момент времени система находится в равновесии, отсутствуют турбулентные потоки и прочие уменьшающие полезную работу и рассеивающие энергию штуки; работа равновесного процесса всегда больше работы неравновесного) и обратимо (т.е., процесс можно развидеть: провести его в обратном направлении так, чтобы и в системе, и в окружающей среде стало, как было; пример обратимого процесса — поглощение и испускание фотона одной и той же длины волны электроном, необратимого — нагрев тела), а о второй ничего неизвестно. Первая машина работает в обратном направлении, т.е. с помощью работы внешней среды над ней передаёт тепло от холодильника к нагревателю, вторая работает в обычном режиме. Холодильники и нагреватели машин соединены, , а совершаемая работа равна по модулю:

т.е., работа, совершаемая второй машиной, идет на перенос тепла от холодильника к нагревателю первой (помним, что теплота, полученная телом, положительна, теплота, отданная окружающей среде, — отрицательна, работа, совершенная телом, — положительна, работа, совершенная над телом, — отрицательна; в формуле КПД все знаки уже учтены, поэтому теплоты берутся по модулю).
Пусть КПД второй машины больше, чем КПД первой, тогда с учётом (3) имеем:


Итак, в ходе всех перипетий и хитросплетений сюжета нагреватель получил теплоту QнI-QнII, а холодильник отдал теплоту QхI-QхII. Обе эти величины больше нуля, а суммарная работа обеих машин этому самому нулю равна. Т.е., кроме того, что теплота была перенесена от холодильника к нагревателю, не произошло больше ничего! Посмотрев ещё раз на постулат Клаузиуса, можно успокоиться и сказать, что такого не бывает.
Логично предположить, что условие (4) неверно, а значит, верно:

Если вторая машина работает равновесно и обратимо, то система становится симметричной, т.е. первую и вторую машину можно поменять ролями и ничего не изменится. Очевидно, этому случаю отвечает знак равенства. Отсюда можно сделать вывод о том, что КПД машины, работающей по циклу Карно, не зависит от природы рабочего тела. Таким образом, для установления формулы КПД достаточно рассмотреть любой частный случай. Уравнение (1) было получено из решения для идеального газа. Также можно сделать вывод о том, что КПД (как и работа) машины, работающей необратимо и неравновесно, меньше КПД машины, работающей обратимо и равновесно.
Из уравнения (1):

или

Алгебраическая сумма отношений теплот процесса к их температурам для цикла Карно равна нулю.
Любой циклический процесс можно разбить на множество бесконечно малых циклов Карно, и тогда предыдущее условие преобразится в:

Функции, изменение которых в результате любого циклического процесса равно нулю, называют функциями состояния. Их значение не зависит от пути процесса, а определяется только конечным состоянием.
Функцию состояния системы, изменение которой в ходе равновесного процесса равно отношению теплоты процесса к температуре его протекания, назвали энтропией:

(знак равенства относится к равновесным процессам, а знак больше — к неравновесным).
Если система изолирована, то есть не обменивается с окружающей средой ни веществом, ни энергией, то Q=0 (система не обменивается теплотой с окружающей средой), тогда:

или энтропия изолированной системы возрастает в неравновесных процессах и остаётся прежней в равновесных, или энтропия изолированной системы не убывает.
Amen. Мы дошли до той самой формулировки второго начала термодинамики!
Итого, из сказанного выше, никак нельзя сказать, что энтропия — мера чего-либо, это просто функция. Расти всегда она не обязана, никто не запрещает ей убивать убывать.
По пути мы решили ту самую задачку про моли (да придётся пролистать назад, я и сам её забыл, всё-таки, термодинамика — захватывающая штука!). Чтобы решить, в какую сторону пойдёт реакция, нужно изолировать систему и посчитать изменение энтропии в ходе процесса: будет убывать — туда не пойдёт, будет возрастать — туда пойдёт, ну и остаётся вариант с равновесием, чтобы остановиться и передохнуть.
Что ж, с байкой про «энтропия всегда растёт» всё ясно: кто-то не дочитал «изолированной системы», но поспешил нести истину © в массы. А вот что с «мерой хаоса»? Я покажу вам ещё один подход.
The second father
Обратимся к статистике. Допустим, у нас есть N шариков, которые могут располагаться на двух разных уровнях относительно земли, ёмкость первого уровня N1, второго — N-N1. Сколькими способами можно разместить эти шарики? Очевидно, это число сочетаний без повторений (порядок размещения на уровне неважен, но каждый шар — индивидуальность и считается отдельно, можете представить их пронумерованными):

По сути мы записали число микросостояний (расположение конкретных шариков по уровням), через которые возможно достижение одного и того же макросостояния (N1 шарик находится на первом уровне относительно земли, а N2 шариков — на втором). Такое число называется термодинамической вероятностью. От обычной вероятности она отличается тем, что её забыли поделить на общее число микросостояний всех возможных макросостояний, т.е. если варьировать N1 и складывать все W при постоянном числе уровней и N.
Перейдём от букв к цифрам. Пусть уровня всё ещё 2, шариков всего 40, уровни при этом вырождены (т.е. шарикам без разницы, на каком именно находиться), а шарики случайным образом перемещаются между ними. Термодинамическая вероятность распределения »20 там и 20 там» равна 14.0×1010, а »19 к 21» — 13.3×1010. То есть шанс посмотреть и увидеть »20 к 20» всего в 1.053 раза больше, чем »21 к 19», хотя интуитивно мы воспринимаем распределение пополам гораздо более вероятным, чем перевес. Вот что теорвер животворящий делает!
Но поглазели и хватит, вернёмся к теме разговора. Термодинамическая вероятность тоже позволяет судить о пути протекания процесса: если мы идём из состояния (макросостояния), W которого ничтожно мала, к состоянию с огромным ЧСВ W, то можно уверенно сказать, что процесс пойдёт. Верно и обратное. Осталось связать W и S. Ничего сложного, тем более за нас это сделал Больцман:

где k — постоянная Больцмана.

Кхмкхм произведения равно/равен/равна сумме кхмкхм. Знакомое соотношение? И Больцману оно показалось знакомым! И он вывел на листе уравнение имени себя с постоянной имени себя. Последнюю, кстати, найти также несложно: мы не ограничивали никак до сих пор (и далее не будем) набор объектов, которые подчиняются этому уравнению, и для всех этих объектов постоянная одна и та же, значит, можно взять частный случай, посчитать постоянную для него и утвердить её кандидатуру. Частным случаем, кстати, был вновь выбран идеальный газ.
Обнаружив такую связь, можно определённо заявить, что с ростом энтропии растёт термодинамическая вероятность, то есть растёт количество вариантов на микроуровне, которые реализуют один вариант на макроуровне. Такое огромное число вариантов реализации одного состояния некоторые назвают хаосом, но я сделать это никак не возмусь. Весь этот «хаос» подчинен закономерностям и Великому Рандому, который не хаос, а именно что Господин Случай. Я бы назвал энтропию — с точки зрения вероятностного подхода — мерой инвариантности системы и вам советую поступать так же!
Дописанная пятая страница в wordе мне подсказывает, что пора закругляться, хотя хотелось бы ещё сказать пару слов о границах применимости энтропии, её характере и тепловой смерти Вселенной. Но это потом, а сейчас пора спать…
Литература
1. Герасимов Я.И. и др. «Курс физической химии», том 1 — Москва, из-во «Химия», 1964 г. — 624 с.
