[Из песочницы] Теория игр и её применение в жизни
Привет, читатель!
Некоторые из вас видели набор букв«qwerty». Qwerty — это раскладка клавиатуры. Посмотрите на вашу клавиатуру. Вы увидите в верхнем ряду буквы «q«w"e«r"t«y». А по какой причине нам интересна раскладка клавиатуры?
Ещё давно, когда люди пользовались печатными машинками, печатали они довольно быстро. Это создавало проблемы: головки печатной машинки, бьющие по бумаге и печатающие на ней буквы, цеплялись друг за друга, что приводило к поломке. Была создана раскладка qwerty, в которой рядом стоящие в словах буквы были размещены на максимально большом расстоянии друг от друга. Таким образом была решена проблема.
Печатными машинками давно никто не пользуется, и проблема соприкосновения печатающих головок исчезла. Факт того, что мы перестали пользоваться неудобной раскладкой клавиатуры логичен. Но, есть загвоздка — такого факта не существует, люди привыкли печатать на раскладке «qwerty» и не хотят переучиваться.
Сейчас, зайдя в настройки, вы можете переключить раскладку клавиатуры на «dvorak». Печать ускорится в разы, в то время как обучение займёт лишь неделю. К сожалению, никому не выгодно быть единственным переучившимся, потому что за любым компьютером, кроме личного, работать будет неудобно. А также, к сожалению или к счастью, людям лень переучиваться. Хотя вместе, приложив усилия и переучившись, мы могли бы увеличить пропускную способность набора текста в разы.
Подводя итоги: при массовом использовании «qwerty», переход отдельного игрока на «dvorak» не эффективен, хотя переход общества на «dvorak» эффективен.
Понятие «Теория игр»
Теория игр изучает конфликты двух или более сторон, именуемых играми. Под изучение попадают сами игры, стратегии, применяемые в играх, а также модели поведения в играх. Поведение игроков обусловлено стратегиями. Стратегии, присущие игрокам носят название «модели поведения».
Возьмём пример:
Есть автомат, который реагирует на ваши действия. Если вы положите в него монетку, ваш противник получит три монеты — и наоборот, если ваш противник положит монетку в автомат, вы получите 3 монетки.
В данном случае, в игре присутствуют 2 игрока — «Наивный» и «Стратег». Они могут доверять противнику, следовательно положить монетку или обмануть и не положить монетку.
Что произойдёт? Если первый игрок и его противник доверятся, то первый игрок получит 3 монеты, отдав 1 и его противник получит 3 монеты отдав 1. Если игрок номер 1 доверится, а противник обманет, то игрок ничего не получит, отдав 1 монету. Если первый игрок обманет, а противник доверится, то игрок получит 3 монеты, не потратив ни одной. Если оба участника попробуют обмануть, то они ничего не получат.
Для удобства игрока 1 обозначим И1, а игрока 2 обозначим И2.
Таблица:
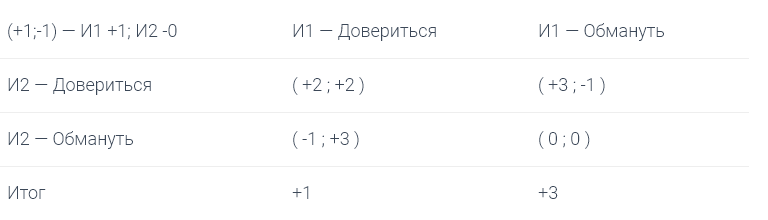
На таблице мы наглядно видим возможные варианты развития игр, далее мы построим множество подобных таблиц. Какие выводы из таблицы мы можем сделать?
Давайте, попробуем найти самую выгодную стратегию — план, следуя которому, мы получим наибольшую выгоду. Так какая из стратегий самая выгодная?
Если противник доверится, И1, выбрав стратегию «Обмануть» получит наивысший выигрыш. Если противник обманет нас, то стратегия «Обмануть» так же выигрывает. Хоть это и жестоко, но стратегия обманывать всегда является наилучшей.
А что же такое модели поведения? Это стратегии, которые постоянно используют определённые игроки. Вспомним имена наших игроков — «Стратег» и «Наивный». Возможно, их имена были даны исходя из стратегий, которые они используют? Да, это так. И вот какие стратегии используют игроки: «Стратег» смотрит на предыдущее действие оппонента и анализирует его, «Наивный» в свою очередь всегда доверяет.
Так же необходимо упомянуть равновесие по Нешу. Равновесие по Нешу — ситуация, в которой ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники свои стратегии не меняют. Помните вступление? А именно игру «qwerty». Если бы все пользователи гаджетов переучились на dvorak, обществу стало бы лучше, но отнюдь, переучиваться лишь нескольким игрокам не выгодно — это и есть равновесие по Нешу.
Термины и типы игр
Теория игр — раздел математической экономики. Изучает конфликты, их решение.
Игра — конфликт двух или более сторон, в котором каждая из сторон преследует свои личные интересы.
Исход игры — выигрыш, проигрыш либо ничья, так же полученное вознаграждение.
Стратегия — умозаключения, из которых исходит выбор действий в игре.
Модель поведения — присущая игроку стратегия либо стратегии.
Равновесие Неша — Так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники свои стратегии не меняют. Часто в играх с равновесием, изменение стратегии всех участников приведёт к увеличению выигрыша, но каждому отдельно взятому участнику игры невыгодно менять стратегию.
Кооперативные и некооперативные. Игра называется кооперативной, когда игроки могут объединяться в группы, брать на себя обязательства перед другими игроками и координировать свои действия. В отличии от кооперативных игр, некооперативные — это игры, где каждый должен играть только за себя. Гибридные игры включают элементы кооперативных и некооперативных игр. Это означает, что каждый игрок будет преследовать интересы своей группы и в то же время попытаться получить личную прибыль.
Симметричные и несимметричные. Игра симметричная, когда игроки будут иметь соответственно одинаковые вознаграждения. Иначе говоря, если игроки поменяются местами, при этом получат выигрыши за одни и те же ходы, что и не меняясь местами. Многие изучаемые игры для двух игроков — симметричные.
С нулевой суммой и с ненулевой суммой. Игры с нулевой суммой — игры с постоянным фондом игры, доступные ресурсы игры не могут стать больше или меньше. В этом случае сумма всех выигрышей равна сумме всех проигравших за каждый ход. Пример такой игры — покер. В играх с ненулевой суммой выигрыш одного игрока не обязательно означает потерю другого игрока. Результат такой игры может быть меньше или больше нуля.
Параллельные и последовательные. В параллельных играх все игроки могут совершить действие в данный отрезок времени. Все стороны совершают свой ход в данный всем промежуток времени, не зная действия оппонентов, до момента завершения игры. В последовательных играх участники могут делать ходы в заранее установленном либо случайном порядке, но при этом они получают некоторую информацию о предшествующих действиях других.
С полной или неполной информацией. В игре с полной информацией участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников. Полная информация недоступна в параллельных играх. В игре с неполной информацией, игроки располагают лишь частичной информацией о противнике.
Игры с бесконечным числом шагов. Игры с бесконечным количеством шагов, как следует из названия, не имеют ограничения в количестве шагов. Игры с конечным количеством шагов — полная противоположность, они ограниченны количеством их.
Дискретные и непрерывные игры. Дискретные игры — игры с ограниченным количеством шагов, событий, исходов. Непрерывные игры — игры, продолжающиеся бесконечное количество времени.
Разбор игр
Игра «Ультиматум»
Играют 1 раз. Есть 2 игрока. Первый может поделить сумму 200 дециллионов франков между собой и противником. Противник может согласиться с решением первого игрока — разделить выигрыш, либо отказаться. В случае отказа, никто ничего не получает.
Давайте, классифицируем игру!
Это некооперативная игра, т.к. нельзя объединяться в группы. Это не симметричная игра, т.к. 1 и 2 игроки имеют разные действия в игре. Это игра с не нулевой суммой, ведь весь выигрыш может пропасть. Это последовательная игра, т.к. решения принимаются по очереди — 1, а затем 2 игрок. Это игра с полной информацией, т.к. второму игроку доступна информация о действиях первого игрока. Это игра с не бесконечным количеством шагов — лишь 2 шага. Это дискретная игра, т.к. число действий ограниченно.
Мы играем за 1 игрока. Как выбрать стратегию? Представим возможные развития.
n > 0: Любой разумный игрок согласится поделить выигрыш, ведь никто не откажется стать вторым или даже первым самым богатым человеком нашей планеты.
n = 0: Игрок может как согласиться, так и отказаться.
Таким образом оптимальная стратегия для 1 игрока — предложить противнику 1 дециллион франков, забрав оставшиеся 199 себе.
Игра «Охота на оленя»
Суть игры — группа охотников из 2 человек вышла на охоту за оленем в края с очень большим количеством зайцев. Цель охотников — убить оленя. Цель каждого игрока — убить добычу. Хоть наивысшая выгода для всех игроков — олень, каждый из охотников может убить зайца, получив личную выгоду, но спугнув оленя.
Классификация.
Это кооперативная игра — игроки могут объединяться в группы. Это симметричная игра, т.к. игроки имеют одинаковый выбор действий. Это игра с ненулевой суммой, ведь весь выигрыш варьируется. Это параллельная игра, т.к. решения принимаются в один и тот же промежуток, произвольно. Это игра с полной информацией, т.к. обеим игрокам доступна информация о действиях друг друга. Это игра с небесконечным количеством шагов — доступен лишь 1 шаг. Это дискретная игр, т.к. число действий ограниченно.
Построим схему:

Вознаграждение за оленя однозначно выше, но шанс остаться ни с чем высок. Играя с надёжным напарником, которому можно доверять, вы можете договориться убить оленя. В ином случае лучше выбрать стратегию «Заяц».
Игра «Бототто»
Играют 2 игрока. Каждый из них может написать 3 цифры, но не в порядке убывания. Сумма цифр должна равняться 6. Игрок, 2 позиции цифр которого превосходят 2 позиции оппонента выигрывает.
Классификация.
Это некооперативная игра — игроки не могут объединяться в группы. Это симметричная игра, т.к. игроки имеют одинаковый выбор действий. Это игра с нулевой суммой, ведь весь выигрыш фиксирован. Это параллельная игра, т.к. решения принимаются в один и тот же промежуток, произвольно. Это игра с неполной информацией, т.к. обеим игрокам не доступна информация о действии оппонента. Это игра с не бесконечным количеством шагов — лишь 1 шаг. Это дискретная игра, т.к. число действий ограниченно.
Выбор стратегии.
Есть 3 варианта действий за каждого игрока (игра симметрична):
(2–2–2) или (1–2–3) или (1–1–4).
(1–1–4) против (1–2–3) влечёт ничью.
(1–2–3) против (2–2–2) влечёт ничью.
(2–2–2) бьёт (1–1–4).
Таким образом (2–2–2) и есть оптимальная стратегия.
В этой игре так же есть равновесие Наша: любая комбинация стратегий (2–2–2) и (1–2–3).
Игра «Принцесса и Чудовище»
В тёмной, тёмной пещере… Тёмной, тёмной ночью… Тёмное, тёмное чудовище… Искало тёмную, тёмную принцессу… Тёмная, тёмная пещера имела тёмные, тёмные границы известные тёмным, тёмным игрокам…
Проще говоря, принцесса вместе с чудовищем появилась в пещере, границы которой известны как принцессе, так и чудовищу. Цель чудовища — поймать принцессу, а цель принцессы — продержаться как можно дольше. Чудовище может схватить принцессу на маленькой дистанции относительно размера пещеры. Оба игрока имеют свободу перемещения.
Классификация игры
Это некооперативная игра — игроки не могут объединяться в группы. Это не симметричная игра, т.к. игроки не имеют одинаковый выбор действий. Это игра с нулевой суммой, ведь весь выигрыш фиксирован. Это параллельная игра, т.к. решения принимаются в один и тот же промежуток, произвольно. Это игра с неполной информацией, т.к. обеим игрокам не доступна информация о действиях друг друга. Это игра с бесконечным количеством шагов — шаги не ограниченны. Это игра с бесконечным количеством шагов, т.к. число действий не ограничено.
Решение игры
Эта игра не была решена до конца 1970-х годов. Но позже была найдена стратегия. Стратегия для принцессы заключается в следующем: принцесса идёт в случайную точку и ждёт в этой точке определенное количество времени, не слишком короткое и не слишком длинное. Затем принцесса перемещается в другую случайную точку и так далее.
Для монстра предлагается оптимальная стратегия поиска, при которой вся комната делится на множество маленьких прямоугольников. Монстр случайным образом выбирает прямоугольник и ищет в нём, затем случайным образом выбирает следующий прямоугольник и так далее.
Кстати, очевидная стратегия — начать со случайного конца и зигзагообразно отрезать путь отступления — неоптимальная.
Игра «Угадай 2/3 среднего»
В 2005 году датская газета под названием «Politiken» предложила своим читателям сыграть в следующую игру: любой желающий мог отправить издателю действительное число от 0 до 100, отправитель самого близкого к 2/3 от среднего арифметического числа из отправленных чисел выигрывал 5000 датских крон.
Эта игра демонстрирует разницу между абсолютно рациональным поведением и реальными действиями игроков.
Представьте, что все участники игры действуют рационально и знают, что все остальные участники рациональны. Какое число является оптимальным в этой ситуации?
Очевидно, что нет смысла называть число больше 66. (6) потому что две трети от среднего арифметического не могут быть больше. Однако, если все игроки думают таким образом, все числа будут не более 2/3×66.(6) = 44.(4). Повторяя данное рассуждение бесконечно много раз, мы придём к выводу, что единственным правильным ходом будет число 0. Поэтому, если все игроки рассуждают рационально, все они должны выбрать число 0.
Однако в реальной жизни ситуация иная. Даже если игрок рационален, он знает, что многие из его противников не рациональны, а значит ему придётся учитывать, что их числа будут больше 0. Можно предположить, что большинство пришлёт более-менее случайные числа, тогда средним будет 50, две трети от 50 приближённо равно 33. Если пойти дальше и предположить, что до числа 33 догадается достаточно много людей, то можно выбрать две трети от 33, т.е. 22. Дальнейшие итерации дадут ~15, ~10 и т.д., но кажется маловероятным, что так далеко будет просчитывать достаточно существенное число игроков.
Игра «Дилемма добровольца»
Игра с дилеммой добровольца моделирует ситуацию, в которой каждый игрок может либо принести небольшую жертву, которая приносит пользу всем, либо вместо этого ждать в надежде извлечь выгоду из чужой жертвы.
Одним из примеров является сценарий, в котором электроснабжение отключилось для всего района. Все жители знают, что электроэнергетическая компания не решит проблему до тех пор, пока не позвонит и не уведомит о случившемся хотя бы один человек, заплатив за звонок. Если никто не желает звонить, отрицательный выигрыш получат все участники. Если какой-либо человек решит стать добровольцем, остальные выиграют, конечно, если не станут добровольцами.
В этой игре игроки самостоятельно решают, стоит ли жертвовать собой ради блага группы. Если никто не жертвует чем-то добровольно, все проигрывают.
Как бы мы не старались, найти выигрышную стратегию, играя с рациональными игроками, мы не можем. Но что будет в жизни? Ведь не все люди рациональны!
История Теории игр
Уже в 18 веке были предложены оптимальные решения и стратегии для математического моделирования. Некоторые задачи были рассмотрены в 19 веке Августином Августином Круно и Жозефом Луи Франсуа Бертаном.
В начале 20-го века Эммануил Ласкер, Эрнст Фиридрих Джемело и Фердинанд Феликс Эдуард Джастин Эмиль Борель выдвинули идею математической теории конфликта интересов.
Математическая теория игр происходит из неоклассической экономики. Впервые математические аспекты и приложения теории были представлены в классической книге Джона фон Неймана и Оскара Моргенштерна 1944 года «Теория игр и экономическое поведение».
Эта область математики нашла некоторые отражения в общественной культуре. Американский писатель и журналист Сильвия Назар в 1998 году опубликовала книгу о судьбе Джона Форбса Нэша, а в 2001 году по мотивам книги был снят фильм «Игры разума».
После окончания Политехнического института Карнеги с двумя степенями — бакалавр и магистр — Джон Нэш поступил в Принстонский университет, где он посещал лекции Джона фон Неймана. В своих трудах Нэш разработал принципы «динамики управления». Джон Нэш защитил докторскую степень по теории игр в 1949 году и был награждён Нобелевской премией по экономике.
Первые концепции теории игр анализировали антагонистические игры, когда есть проигравшие и выигравшие за их счёт игроки. Нэш разрабатывает методы анализа, в которых все участники либо выигрывают, либо проигрывают.
Эти ситуации называются «равновесием по Нэшу» или «некооперативным равновесием», когда стороны используют оптимальную стратегию, что приводит к созданию устойчивого равновесия. Игрокам выгодно поддерживать этот баланс, так как любое изменение ухудшит их ситуацию.
Данные работы Нэша внесли значительный вклад в развитие теории игр, и математические инструменты для экономического моделирования были пересмотрены. Нэш показывает, что классический подход к конкуренции Адама Смита, когда каждый сам за себя, не оптимален. Стратегии более выгодны, когда каждый пытается получить пользу для себя и сделать лучше для других.
Хотя теория игр первоначально рассматривала экономические модели, она оставалась формальной теорией в рамках математики до 1950-х годов. Но уже в 1950-х годах были приняты попытки применить методы теории игр не только в экономике, но и в биологии, кибернетике, технологиях и антропологии.
Во время Второй мировой войны и сразу после неё теорией игр серьёзно заинтересовались военные, которые увидели в ней мощный аппарат для исследования стратегических решений.
В 1960–1970 годах интерес к теории игр ослаб, несмотря на значительные математические результаты, достигнутые к тому времени. С середины 1980-х годов началось активное практическое применение теории игр, особенно в области экономики и управления.
За последние 20–30 лет важность теории игр и интерес к ней значительно возросли. Некоторые области современной экономической теории не могут быть изложены без применения теории игр.
Ряд известных учёных стали лауреатами Нобелевской премии по экономике за их вклад в развитие теории игр, которая описывает социально-экономические процессы. Джон Нэш, благодаря своим исследованиям в теории игр, стал одним из ведущих специалистов в области ведения «холодной войны», что подтверждает масштабность задач, которыми занимается теория игр.
Лауреатами премии по экономике памяти Альфреда Нобеля за достижения в области теории игр и экономической теории стали: Роберт Ауман, Райнхард Зелтен, Джон Нэш, Джон Харсаньи, Уильям Викри, Джеймс Миррлис, Томас Шеллинг, Джордж Акерлоф, Майкл Спенс, Джозеф Стиглиц, Леонид Гурвиц, Эрик Мэскин, Роджер Майерсон, Ллойд Шепли, Элвин Рот, Жан Тироль.
Применение Теории игр в жизни
Игра «Пробка»
Пробка из бутылки шампанского выстрелила так сильно, что долетела до телефона с открытым навигатором.
Представим ситуацию, что у вас есть выбор: либо ехать по шоссе в период пробки, либо выбрать пустой окружной путь, который в 2 раза длиннее, чем шоссе. Максимальная допустимая скорость в условиях пробки в 3 раза меньше максимальной допустимой скорости, без неё.
Здесь всё просто. Длинна пути — x, скорость — y.
Пробка — 1 x / 1 y
Пустая дорога — 2 x / 3 y
Попробуем подставить числа.
Пробка — 50 / 10 = 5
Пустая дорога 100 / 30 = 3.3
Попробуем другие, отличные от предыдущих чисел.
Пробка — 100 / 320 = 0.3
Пустая дорога — 200 / 960 = 0.2
Согласно результатам, мы можем сделать вывод: в любом случае пустая дорога будет быстрее.
Но это ещё не всё, у этого опыта есть продолжение. Множество людей, сами того не зная, воспользуются теорией игр и выберут пустую дорогу, которая в свою очередь станет загруженной. Учтя это, возможно вы выберите первый вариант, проанализировав некоторые факторы: среднее прибывание машин, вместимость дорог, время, необходимое для образования пробки и время приближения к развилке дорог.
Игра «Игра Мафия»
Вы с друзьями играете в Мафию. Остаются в живых: «Мирный житель», «Мафиози» и «Маньяк». Какие шансы выиграть мирному? Казалось бы — никаких.
Как мы видим, если:
Мафия убьёт Маньяка, и Маньяк убьёт Мафию — Выиграет Мирный.
Мафия убьёт Маньяка, и Маньяк убьёт Мирного — Выиграет Мафия.
Мафия убьёт Мирного, и Маньяк убьёт Мафию — Выиграет Маньяк.
Мафия убьёт Мирного, и Маньяк убьёт Мирного — Ничья.
Если решения спонтанны и случайны, шансы мирного — 25%
Конечно, никто не хочет иметь шанс либо проиграть, либо получить ничью, т.к. шанс либо проиграть, либо выиграть лучше. Следственно выбор убить мирного исключается. Следственно Мафия убьёт Маньяка и Маньяк убьёт Мафию — Выиграет Мирный.
Игра «Фильм»
Представите — после продолжительного рабочего дня вы возвращаетесь домой, в надежде лечь спать сразу после приезда. Поездка будет длиться 1 час 50 минут. Внезапно у вас появилось желание посмотреть фильм, а в стриминговом сервисе остался последний купон на фильм. У вас есть выбор из 2 фильмов: один из них — «Матрица», идущий 2 часа, второй — «Омерзительная Восьмёрка», идущий 3 часа. Также, последний вы очень хотели посмотреть.
Итак, попробуем понять, что нам смотреть. Важно учесть — следующие купоны на фильмы вы получите лишь через неделю.
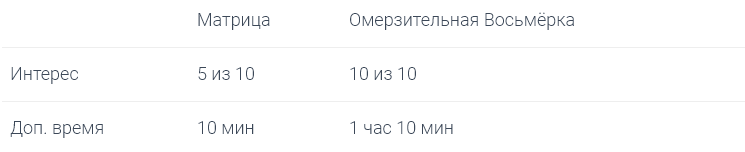
Ваш интерес к Омерзительной Восьмёрке очень велик, но, к сожалению, мы не можем перевести интерес и желание спать в одну величину и сравнить их, т.к. это очень персонально и зависит от множества факторов: таких как: желания спать, времени пробуждения, важности завтрашних дел, возможности посмотреть фильм в иное время, уровня заряда аккумулятора телефона и т.д.
К счастью, человеческий мозг может обрабатывать огромное количество информации. Но создание универсального пути решения, даже столь простой для нас задачи — это очень сложно и требует большого запаса времени и ресурсов.
Игра «Неблагоприятная монополия»
Пожалуй, это одна из самых распространённых игр в мире экономики. Напомним, что теория игр — раздел математической экономики.
Майкрософт, Сони, Дисней… Угадайте общую черту этих корпораций? Каждый из них в той или иной степени монополист на своём рынке. Майкрософт, а именно Windows в сфере операционных систем. Сони, если быть точнее — Play Station, в сфере игровых приставок. Дисней в сфере развлекательного кино.
Все 3 компании управляют большей частью рынка, регулируя и задавая стандарты. Некогда они совершили переворот, произвели то, что стало вершиной возможностей. Можно вспомнить некоторые операционные системы Майкрософт, Play Station 2 и игру The Last of Us, мультики Диснея, популярные во всём мире.
Но, корпорации в первую очередь интересуются прибылью. Завоевав рынок и закрепив за собой статус, они начали производить достаточно посредственные продукты и услуги. Windows 8 и проблемы Windows 10, Play Station Vita, Мстители — посредственные продукты, не заслуживающие их статуса.
Клиенты, объединившись, могут заставить компании изменить стратегию — начать производить более качественную продукцию. Отказавшись от услуг и продуктов компании, клиенты могли бы сократить рынок, заставив компанию найти пути возвращения рынка.
Но, к сожалению, люди, в отличии от птиц и некоторых других созданий, не наделены способностью объединяться настолько продуктивно и слаженно.
Шансы вышеописанной ситуации очень скудны. И игроки это понимают.
Каждому участнику игры не выгодно отказываться от Windows, ведь большинство игроков привыкли к нему и им будит сложно не только разобраться, и не только установить Linux, но и понять различия между Linux Kali и Linux Ubuntu.
Каждому участнику игры не выгодно отказываться от того либо иного продукта, т.к. он знает, что личной выгоды не извлечёт.
В основе этой игры лежит «Равновесие Неша», с которым мы уже знакомы. Но давайте обновим наши возможно искажённые воспоминания!
Равновесие Неша — набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники свои стратегии не меняют.
Конечно, мы можем представить ситуацию, в которой прежние клиенты вышеуказанных компаний отказались от продукции наших компаний.
В этом случае Майкрософт, Сони, Дисней создали бы продукты такого качества и таких возможностей, которые и каких будит необходимо для возвращения рынка.
Возможно, ими бы стали: «Windows Infinity с открытым исходным кодом», «игры не только с Киану Ривзом и Норманом Ридусом, а со всем Голливудом, в дополнении с Квентином Тарантино в качестве режиссёра», «Мстители со смыслом и хорошим сюжетом».
Увы, но это не достижимо. Это равновесие Неша размерами исчисляемыми 100 миллионами участников, решить очень затруднительно.
Так же хотелось бы отметить некоторые детали:
Не только «наша троица» располагает таким положением. Сотни и сотни компаний играют в эту игру.
Существуют разные виды этой игры. Иногда корпорация не занимает монополистическое положение, но имеет круг «преданных» клиентов, либо лишь их продукты предоставляют определённые возможности. Пример тому — Apple.
Игра «Модель Бертрана»
Выгодно ли магазинам снижать цену на продукт? Очевидно, что нет, но не всё так просто.
Представим игру — 2 магазина продают один и тот же товар с наценкой в 20%, покупая его у производителя по одной и той же цене. Одинаковая цена = одинаковый спрос = одинаковый заработок.
Внезапно один из магазинов понижает цену. Что произойдёт? У него появится больший спрос и следственно больший заработок. Вот почему снижение цены иного бывает прибыльно.
Игра «Узкая дорога»
Икс и Игрик едут навстречу друг другу по узкой дороге. Что бы не врезаться друг в друга обоим необходимо съехать на обочину.
Игра заключается в выборе стороны поворота. Каждый из игроков должен выбрать сторону, не совпадающую с стороной противника. Что выбрать? Для решения такой игры созданы правила дорожного движения.
Применение Теории Игр
Зачем нужна теория игр? В разделе «История» вы могли наблюдать развитие теории игр и упоминания её применения. Так давайте выясним, зачем нужна теория игр, где её применяют, и даже, как теория игр может пригодиться вам!
Биология
Для начала нужно отметить: поведение животных в значительной степени определяется генетически, также, некоторые виды поведения более соответствуют ситуации, чем другие.
Распространена частично неверная мысль «выживают наиболее приспособленные», не менее высший критерий биологической приспособленности — не выживание, а репродуктивный успех.
Животные передают свои гены следующему. Затем, более адаптируемый фенотип становится относительно большим в следующем поколении, чем менее адаптируемый фенотип. Именно этот процесс отбора изменяет комбинацию генотипа и фенотипа и может в конечном итоге привести к формированию стабильного состояния.
Новые генетические мутации происходят время от времени, спонтанно. Многие из них создают фенотип, который плохо сочетается с окружающей средой и поэтому исчезает. Однако, иногда мутации могут приводить к новым фенотипам, делая их более адаптивными к окружающей среде.
Количество более приспособленных мутаций животных будет расти в то время, как неприспособленные могут исчезнуть, а мутации, в настоящий момент не входящие в состав данной популяции, могут попытаться её захватить.
Аналогичные ситуации используются и в теории игр. Поведение можно рассматривать как стратегию взаимодействия животных с другими животными. Единственное отличие — у животных выбор стратегии не осуществляется с помощью целенаправленных решений.
Социология и психология
Теория игр применяется в социологии с целью понять, объяснить и контролировать игры с социальной составляющей. В стою очередь в психологии теория игр изучает действия каждого отдельного обособленного игрока. В той или иной форме теорию игр используют психологи, социологи, политики, маркетологи и многие другие люди.
Социологи пытаются понять причины действий групп игроков и использовать полученные знания. Они моделируют игры, проводят исследования, чтобы найти наиболее выгодную стратегию.
Политика
В политике теория игр применяется для анализа ситуаций и взаимодействий игроков (как правило стран), для решения игр и для поиска наилучших стратегий. У стран есть ряд конфликтов: территории, торговля, альянсы… Теория игр помогает достичь компромисса.
Так же теория игр применяется в голосованиях — кандидаты прибегают к разным стратегиям для увеличения шансов выигрыша.
Экономика
В экономике теория игр применяется повсеместно. Ранее вы встретили игру «Неблагоприятная монополия», это очень хороший пример игры. Экономические игры — аукционы, модели монополии и олигополии, рынки и многое другое.
В экономике существуют модели, которые характеризуют те или иные игры и являются универсальными — и могут быть применены во всех играх, подходящих по характеристике.
Неосознанное применение
Часто, мы применяем теорию игр, даже не догадываясь об этом. Мы выстраиваем логически цепочки, анализируем ситуации и придумываем стратегии, используя теорию игр, но не зная об этом. Выше, приведены игры «Фильм», «Пробка» и некоторые другие, в которых игроки играют постоянно.
Наш мозг анализирует игры, не предавая этому значение. Из этого утверждения вытекает вопрос: может ли знание теории игр пригодиться обычному человеку?
Польза знания Теории Игр
Теория игр полезна множеству разных специалистов, но нужна ли Теория Игр обычном человеку?
Практического повсеместного применения теории игр для обычного человека нет. В жизни, анализировать игру, стоя с листиком и ручкой напротив прилавка с печеньем, выбирая товар — не лучшая идея, ведь справиться с этой задачей можно и без применения методов теории игр.
Теория игр полезна, когда:
- Важные решения. В нашей жизни бывают ситуации, требующие очень продуманного выбора, который может изменить множество вещей. В таких ситуациях теория игр может быть крайне полезна и даже необходима.
- Логическое мышление, умение мыслить на шаг вперёд. Теория игр показывает, что не всегда наша интуиция верна. Она может научить нас мыслить логически и проверять даже самые очевидные ситуации. Так же теория игр может научить мыслить в более долгосрочной перспективе и учитывать большее количество деталей. Помните игру «Пробка»? Ближе к концу текста, говорилось: «Множество людей, сами того не зная, воспользуются теорией игр и выберут пустую дорогу, которая в свою очередь станет загруженной». Это и есть мышление на несколько ходов вперёд.
- Расширение кругозора. Теория игр может быть интересна, кроме того, теория игр расширяет кругозор. Любое знание полезно, а многогранные знания крайне полезны. Теория игр, не являясь исключением, так же полезна и интересна.
Источники
«Главы | Эволюционные игры» — научный журнал ПостНаука (bit.ly/2HrN02a)
«Теория игр» — Википедия (bit.ly/2Oz6Ltj)
«Угадай 2/3 среднего, %username%» — веб-сайт Хабр (bit.ly/3dJIxWL)
«Теория игр: Введение» — веб-сайт Хабр (bit.ly/35XcPmc)
«Теория игр» — научный журнал ПостНаука (bit.ly/2T0PhHW)
«Список игр теории игр» — Википедия (bit.ly/2DrUOPF)
«Понять за 12 минут: когда теория игр побеждает здравый смысл» — научно-популярный канал (bit.ly/3fPLJBZ)
»10 фактов о теории игр» — профессор Чикагского университета и ВШЭ Константин Сонин (bit.ly/2y4XBPK)
«Игры, которые изучают экономисты» — лекция НИУ ВШЭ (bit.ly/2T2fHcc)
«Теория игр» — курс лекций доктора наук Алексея Савватеева (bit.ly/3fR2o8j)
«Что наша жизнь: 10 примеров того, зачем экономистам нужна теория игр» — научный журнал ПостНаука (bit.ly/2WZjuIu)
