[Из песочницы] Сжатие данных алгоритмом Хаффмана
Вступление
В данной статье я расскажу об известном алгоритме Хаффмана, а также о его применении в сжатии данных.
В результате напишем простенький архиватор. Об этом уже была статья на Хабре, но без практической реализации. Теоретический материал текущего поста взят из книги Роберта Лафоре «Data Structures and Algorithms in Java». Итак, все под кат!
Немного размышлений
В обычном текстовом файле один символ кодируется 8 битами (кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASY\n». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — '\n'. Файл, содержащий данную строку будет весить 22×8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или '\n') — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.
Кодирование
Почему бы символу 'S' не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ' '(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:
Ни один код не должен быть префиксом другого
Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:

Символы с наибольшим количеством вхождений должны кодироваться наименьшим возможным количеством битов. Приведу пример одной из возможных таблиц кодов:

Таким образом, закодированное сообщение будет выглядеть так:
10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110
Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос: как этот салага придумал код как создать таблицу кодов? Об этом пойдет речь ниже.
Построение дерева Хаффмана
Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:
public class Node {
private int frequence;
private char letter;
private Node leftChild;
private Node rightChild;
...
}
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
...
}
Это не полный код, полный код будет ниже.
Вот сам алгоритм построения дерева:
- Создать объект Node для каждого символа из сообщения (строка s1). В нашем случае будет 9 узлов (объектов Node). Каждый узел состоит из двух полей данных: символ и частота
- Создать объект Дерева (BinaryTree) для кажлого из узлов Node. Узел становится корнем дерева.
- Вставить эти деревья в приоритетную очередь. Чем меньше частота, тем больше приоритет. Таким образом, при извлечении всегда выбирается дерво наименьшей частотой.
Далее нужно циклически делать следующее:
- Извлечь два дерева из приоритетной очереди и сделать их потомками нового узла (только что созданного узла без буквы). Частота нового узла равна сумме частот двух деревьев-потомков.
- Для этого узла создать дерево с корнем в данном узле. Вставить это дерево обратно в приоритетную очередь. (Так как у дерева новая частота, то скорее всего она встанет на новое место в очереди)
- Продолжать выполнение шагов 1 и 2, пока в очереди не останется одно дерево — дерево Хаффмана
Рассмотрим данный алгоритм на строке s1:

Здесь символ lf (linefeed) обозначает переход на новую строку.
А что дальше?
Мы получили дерево Хаффмана. Ну окей. И что с ним делать? Его и за бесплатно не возьмут А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.
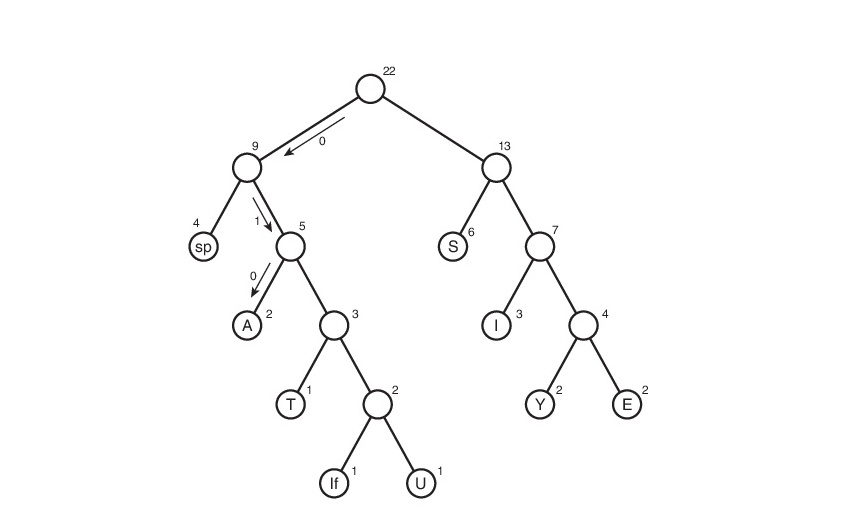
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2×3 + 2×4 + 3×3 + 6×2 + 1×4 + 1×5 + 2×4 + 4×2 + 1×5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.
Декодирование
Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:
0100
111
A1101
E000
I011
S10
T0101
U1100
Y001
Запись таблицы в виде 'символ'«код символа». Почему 0100 без символа? На самом деле он с символом, просто средства java, используемые мной при выводе в файл, символ перехода на новую строку — '\n' -конвертируют в переход на новую строку (как бы это глупо не звучало). Поэтому пустая строка сверху и есть символ для кода 0100. Для кода 111 символом является пробел в начале строки. Сразу скажу, что нашему коэффициенту ханаэтот способ хранения таблицы может претендовать на самый нерациональный. Но он прост для понимания и реализации. С удовольствием выслушаю Ваши рекомендации в комментариях по поводу оптимизации.
Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:
Ни один код не должен являться префиксом другого
Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку (строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.
Реализация
Пришло время унижать мой код писать архиватор. Назовем его Compressor.
Начнем с начала. Первым делом пишем класс Node:
public class Node {
private int frequence;//частота
private char letter;//буква
private Node leftChild;//левый потомок
private Node rightChild;//правый потомок
public Node(char letter, int frequence) { //собственно, конструктор
this.letter = letter;
this.frequence = frequence;
}
public Node() {}//перегрузка конструтора для безымянных узлов(см. выше в разделе о построении дерева Хаффмана)
public void addChild(Node newNode) {//добавить потомка
if (leftChild == null)//если левый пустой=> правый тоже=> добавляем в левый
leftChild = newNode;
else {
if (leftChild.getFrequence() <= newNode.getFrequence()) //в общем, левым потомком
rightChild = newNode;//станет тот, у кого меньше частота
else {
rightChild = leftChild;
leftChild = newNode;
}
}
frequence += newNode.getFrequence();//итоговая частота
}
public Node getLeftChild() {
return leftChild;
}
public Node getRightChild() {
return rightChild;
}
public int getFrequence() {
return frequence;
}
public char getLetter() {
return letter;
}
public boolean isLeaf() {//проверка на лист
return leftChild == null && rightChild == null;
}
}
Теперь деревце:
class BinaryTree {
private Node root;
public BinaryTree() {
root = new Node();
}
public BinaryTree(Node root) {
this.root = root;
}
public int getFrequence() {
return root.getFrequence();
}
public Node getRoot() {
return root;
}
}
Приоритетная очередь:
import java.util.ArrayList;//да-да, очередь будет на базе списка
class PriorityQueue {
private ArrayList data;//список очереди
private int nElems;//кол-во элементов в очереди
public PriorityQueue() {
data = new ArrayList();
nElems = 0;
}
public void insert(BinaryTree newTree) {//вставка
if (nElems == 0)
data.add(newTree);
else {
for (int i = 0; i < nElems; i++) {
if (data.get(i).getFrequence() > newTree.getFrequence()) {//если частота вставляемого дерева меньше
data.add(i, newTree);//чем част. текущего, то cдвигаем все деревья на позициях справа на 1 ячейку
break;//затем ставим новое дерево на позицию текущего
}
if (i == nElems - 1)
data.add(newTree);
}
}
nElems++;//увеличиваем кол-во элементов на 1
}
public BinaryTree remove() {//удаление из очереди
BinaryTree tmp = data.get(0);//копируем удаляемый элемент
data.remove(0);//собственно, удаляем
nElems--;//уменьшаем кол-во элементов на 1
return tmp;//возвращаем удаленный элемент(элемент с наименьшей частотой)
}
}
Класс, создающий дерево Хаффмана:
public class HuffmanTree {
private final byte ENCODING_TABLE_SIZE = 127;//длина кодировочной таблицы
private String myString;//сообщение
private BinaryTree huffmanTree;//дерево Хаффмана
private int[] freqArray;//частотная таблица
private String[] encodingArray;//кодировочная таблица
//----------------constructor----------------------
public HuffmanTree(String newString) {
myString = newString;
freqArray = new int[ENCODING_TABLE_SIZE];
fillFrequenceArray();
huffmanTree = getHuffmanTree();
encodingArray = new String[ENCODING_TABLE_SIZE];
fillEncodingArray(huffmanTree.getRoot(), "", "");
}
//--------------------frequence array------------------------
private void fillFrequenceArray() {
for (int i = 0; i < myString.length(); i++) {
freqArray[(int)myString.charAt(i)]++;
}
}
public int[] getFrequenceArray() {
return freqArray;
}
//------------------------huffman tree creation------------------
private BinaryTree getHuffmanTree() {
PriorityQueue pq = new PriorityQueue();
//алгоритм описан выше
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {//если символ существует в строке
Node newNode = new Node((char) i, freqArray[i]);//то создать для него Node
BinaryTree newTree = new BinaryTree(newNode);//а для Node создать BinaryTree
pq.insert(newTree);//вставить в очередь
}
}
while (true) {
BinaryTree tree1 = pq.remove();//извлечь из очереди первое дерево.
try {
BinaryTree tree2 = pq.remove();//извлечь из очереди второе дерево
Node newNode = new Node();//создать новый Node
newNode.addChild(tree1.getRoot());//сделать его потомками два извлеченных дерева
newNode.addChild(tree2.getRoot());
pq.insert(new BinaryTree(newNode);
} catch (IndexOutOfBoundsException e) {//осталось одно дерево в очереди
return tree1;
}
}
}
public BinaryTree getTree() {
return huffmanTree;
}
//-------------------encoding array------------------
void fillEncodingArray(Node node, String codeBefore, String direction) {//заполнить кодировочную таблицу
if (node.isLeaf()) {
encodingArray[(int)node.getLetter()] = codeBefore + direction;
} else {
fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0");
fillEncodingArray(node.getRightChild(), codeBefore + direction, "1");
}
}
String[] getEncodingArray() {
return encodingArray;
}
public void displayEncodingArray() {//для отладки
fillEncodingArray(huffmanTree.getRoot(), "", "");
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
}
}
System.out.println("========================================================");
}
//-----------------------------------------------------
String getOriginalString() {
return myString;
}
}
Класс, содержащий который кодирует/декодирует:
public class HuffmanOperator {
private final byte ENCODING_TABLE_SIZE = 127;//длина таблицы
private HuffmanTree mainHuffmanTree;//дерево Хаффмана (используется только для сжатия)
private String myString;//исходное сообщение
private int[] freqArray;//частотаная таблица
private String[] encodingArray;//кодировочная таблица
private double ratio;//коэффициент сжатия
public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress
this.mainHuffmanTree = MainHuffmanTree;
myString = mainHuffmanTree.getOriginalString();
encodingArray = mainHuffmanTree.getEncodingArray();
freqArray = mainHuffmanTree.getFrequenceArray();
}
public HuffmanOperator() {}//for extract;
//---------------------------------------compression-----------------------------------------------------------
private String getCompressedString() {
String compressed = "";
String intermidiate = "";//промежуточная строка(без добавочных нулей)
//System.out.println("=============================Compression=======================");
//displayEncodingArray();
for (int i = 0; i < myString.length(); i++) {
intermidiate += encodingArray[myString.charAt(i)];
}
//Мы не можем писать бит в файл. Поэтому нужно сделать длину сообщения кратной 8=>
//нужно добавить нули в конец(можно 1, нет разницы)
byte counter = 0;//количество добавленных в конец нулей (байта в полне хватит: 0<=counter<8<127)
for (int length = intermidiate.length(), delta = 8 - length % 8;
counter < delta ; counter++) {//delta - количество добавленных нулей
intermidiate += "0";
}
//склеить кол-во добавочных нулей в бинарном предаствлении и промежуточную строку
compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate;
//идеализированный коэффициент
setCompressionRatio();
//System.out.println("===============================================================");
return compressed;
}
private void setCompressionRatio() {//посчитать идеализированный коэффициент
double sumA = 0, sumB = 0;//A-the original sum
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
sumA += 8 * freqArray[i];
sumB += encodingArray[i].length() * freqArray[i];
}
}
ratio = sumA / sumB;
}
public byte[] getBytedMsg() {//final compression
StringBuilder compressedString = new StringBuilder(getCompressedString());
byte[] compressedBytes = new byte[compressedString.length() / 8];
for (int i = 0; i < compressedBytes.length; i++) {
compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2);
}
return compressedBytes;
}
//---------------------------------------end of compression----------------------------------------------------------------
//------------------------------------------------------------extract-----------------------------------------------------
public String extract(String compressed, String[] newEncodingArray) {
String decompressed = "";
String current = "";
String delta = "";
encodingArray = newEncodingArray;
//displayEncodingArray();
//получить кол-во вставленных нулей
for (int i = 0; i < 8; i++)
delta += compressed.charAt(i);
int ADDED_ZEROES = Integer.parseInt(delta, 2);
for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) {
//i = 8, т.к. первым байтом у нас идет кол-во вставленных нулей
current += compressed.charAt(i);
for (int j = 0; j < ENCODING_TABLE_SIZE; j++) {
if (current.equals(encodingArray[j])) {//если совпало
decompressed += (char)j;//то добавляем элемент
current = "";//и обнуляем текущую строку
}
}
}
return decompressed;
}
public String getEncodingTable() {
String enc = "";
for (int i = 0; i < encodingArray.length; i++) {
if (freqArray[i] != 0)
enc += (char)i + encodingArray[i] + '\n';
}
return enc;
}
public double getCompressionRatio() {
return ratio;
}
public void displayEncodingArray() {//для отладки
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
//if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
//}
}
System.out.println("========================================================");
}
}
Класс, облегчающий запись в файл:
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.Closeable;
public class FileOutputHelper implements Closeable {
private File outputFile;
private FileOutputStream fileOutputStream;
public FileOutputHelper(File file) throws FileNotFoundException {
outputFile = file;
fileOutputStream = new FileOutputStream(outputFile);
}
public void writeByte(byte msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeBytes(byte[] msg) throws IOException {
fileOutputStream.write(msg);
}
public void writeString(String msg) {
try (PrintWriter pw = new PrintWriter(outputFile)) {
pw.write(msg);
} catch (FileNotFoundException e) {
System.out.println("Неверный путь, или такого файла не существует!");
}
}
@Override
public void close() throws IOException {
fileOutputStream.close();
}
public void finalize() throws IOException {
close();
}
}
Класс, облегчающий чтение из файла:
import java.io.FileInputStream;
import java.io.EOFException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.Closeable;
import java.io.File;
import java.io.IOException;
public class FileInputHelper implements Closeable {
private FileInputStream fileInputStream;
private BufferedReader fileBufferedReader;
public FileInputHelper(File file) throws IOException {
fileInputStream = new FileInputStream(file);
fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream));
}
public byte readByte() throws IOException {
int cur = fileInputStream.read();
if (cur == -1)//если закончился файл
throw new EOFException();
return (byte)cur;
}
public String readLine() throws IOException {
return fileBufferedReader.readLine();
}
@Override
public void close() throws IOException{
fileInputStream.close();
}
}
Ну, и главный класс:
import java.io.File;
import java.nio.charset.MalformedInputException;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.NoSuchFileException;
import java.nio.file.Paths;
import java.util.List;
import java.io.EOFException;
public class Main {
private static final byte ENCODING_TABLE_SIZE = 127;
public static void main(String[] args) throws IOException {
try {//указываем инструкцию с помощью аргументов командной строки
if (args[0].equals("--compress") || args[0].equals("-c"))
compress(args[1]);
else if ((args[0].equals("--extract") || args[0].equals("-x"))
&& (args[2].equals("--table") || args[2].equals("-t"))) {
extract(args[1], args[3]);
}
else
throw new IllegalArgumentException();
} catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) {
System.out.println("Неверный формат ввода аргументов ");
System.out.println("Читайте Readme.txt");
e.printStackTrace();
}
}
public static void compress(String stringPath) throws IOException {
List stringList;
File inputFile = new File(stringPath);
String s = "";
File compressedFile, table;
try {
stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath()));
} catch (NoSuchFileException e) {
System.out.println("Неверный путь, или такого файла не существует!");
return;
} catch (MalformedInputException e) {
System.out.println("Текущая кодировка файла не поддерживается");
return;
}
for (String item : stringList) {
s += item;
s += '\n';
}
HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s));
compressedFile = new File(inputFile.getAbsolutePath() + ".cpr");
compressedFile.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) {
fo.writeBytes(operator.getBytedMsg());
}
//create file with encoding table:
table = new File(inputFile.getAbsolutePath() + ".table.txt");
table.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(table)) {
fo.writeString(operator.getEncodingTable());
}
System.out.println("Путь к сжатому файлу: " + compressedFile.getAbsolutePath());
System.out.println("Путь к кодировочной таблице " + table.getAbsolutePath());
System.out.println("Без таблицы файл будет невозможно извлечь!");
double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//идеализированный коэффициент
double realRatio = Math.round((double) inputFile.length()
/ ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//настоящий коэффициент
System.out.println("Идеализированный коэффициент сжатия равен " + idealRatio);
System.out.println("Коэффициент сжатия с учетом кодировочной таблицы " + realRatio);
}
public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException {
HuffmanOperator operator = new HuffmanOperator();
File compressedFile = new File(filePath),
tableFile = new File(tablePath),
extractedFile = new File(filePath + ".xtr");
String compressed = "";
String[] encodingArray = new String[ENCODING_TABLE_SIZE];
//read compressed file
//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here:
try (FileInputHelper fi = new FileInputHelper(compressedFile)) {
byte b;
while (true) {
b = fi.readByte();//method returns EOFException
compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0");
}
} catch (EOFException e) {
}
//--------------------
//read encoding table:
try (FileInputHelper fi = new FileInputHelper(tableFile)) {
fi.readLine();//skip first empty string
encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n'
while (true) {
String s = fi.readLine();
if (s == null)
throw new EOFException();
encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length());
}
} catch (EOFException ignore) {}
extractedFile.createNewFile();
//extract:
try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) {
fo.writeString(operator.extract(compressed, encodingArray));
}
System.out.println("Путь к распакованному файлу " + extractedFile.getAbsolutePath());
}
}
Файл с инструкциями readme.txt предстоит вам написать самим :-)
Заключение
Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу моей некомпетентности улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!
P.S.
Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли (количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48×8 + 7)=0.38. Если вы тоже это заметили, то только не по лицу вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.
