[Из песочницы] Случайные перестановки и случайные разбиения
Я много лет читаю курсы по комбинаторике и графам для студентов-математиков и computer scientists (как это по-русски, компьютерных научников?), раньше в Академическом университете, а теперь в СПбГУ. Программа у нас построена так, что эти темы проходят как часть «теоретической информатики» (другие темы в ней — алгоритмы, сложность, языки и грамматики). Не могу сказать, насколько это оправдано метафизически или исторически: всё же комбинаторные объекты (графы, системы множеств, перестановки, клетчатые фигуры и др.) начали изучали задолго до появления компьютеров, и сейчас последние хотя и важная, но далеко не единственная причина интереса к ним. Но так посмотреть на самых спецов по комбинаторике и по theoretical computer science — это удивительно часто одни и те же люди: Ловас, Алон, Семереди, Разборов и далее. Наверно, есть на то свои причины. На моих уроках часто очень нетривиальные решения сложных задач предлагают чемпионы олимпиадного программирования (их перечислять не буду, кому любопытно посмотрите топ codeforces.) В общем, думаю, что некоторые вещи из комбинаторики могут быть интересны сообществу. Говорите, если что так или не так.
Пусть вам надо построить случайную перестановку чисел от 1 до $inline$n$inline$, чтобы все перестановки были равновероятны. Это можно сделать многими способами: например, сначала выбрать случайно первый элемент, потом из оставшихся второй и так далее. А можно поступить иначе: выбрать случайно точки $inline$t_1, t_2,\ldots, t_n$inline$ в отрезке $inline$[0,1]$inline$, и посмотреть как они упорядочены. Заменяя наименьшее из чисел на 1, второе на 2 и так далее получаем случайную перестановку. Легко видеть, что все $inline$n!$inline$ перестановок равновероятны. Можно и не в отрезке $inline$0,1$inline$ выбирать точки, а, например, среди чисел от 1 до $inline$N$inline$. Тут возможны совпадения (для отрезка тоже возможны, но с нулевой вероятностью, так что нас они не волнуют) — с ними можно бороться по-разному, например, дополнительно переупорядочивая совпадающие числа. Или взять N побольше, чтобы вероятность совпадения была маленькой (хорошо известен случай, когда $inline$N=365$inline$, а $inline$n$inline$ есть число учеников в вашем классе, и речь о совпадении двух дней рождения.) Вариация этого метода: отметить случайно $inline$n$inline$ точек в единичном квадрате и посмотреть, как упорядочены их ординаты относительно абсцисс. Другая вариация: отметить в отрезке $inline$n-1$inline$ точку и посмотреть, как упорядочены длины отрезочков, на которые он разбился. Ключевой момент в этих подходах — независимость испытаний, по результатам которых строится случайная перестановка. Андрей Николаевич Колмогоров говорил, что теория вероятностей это теория меры плюс независимость — и это подтвердит всякий кто имел дело с вероятностью.
Покажу, как это помогает, на примере формулы крюков для деревьев:
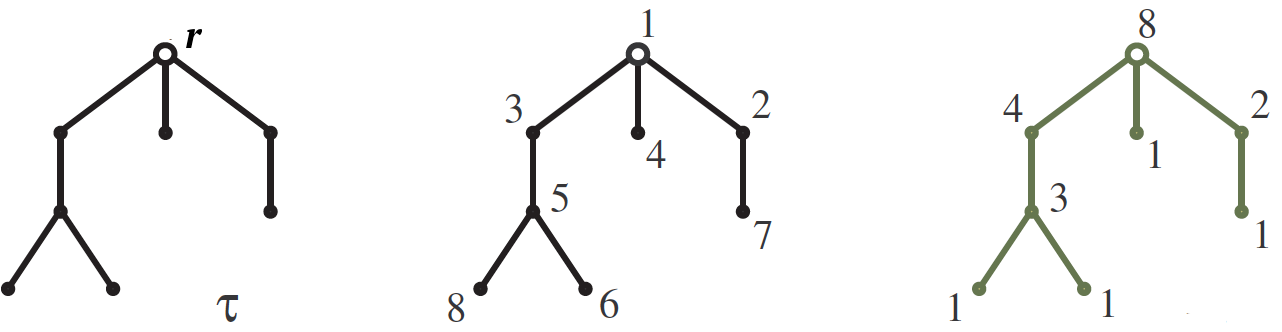
Пусть $inline$\tau$inline$ — подвешенное за корень $inline$r$inline$ дерево с $inline$n$inline$ вершинами, растущее вниз как на картинке. Наша цель — вычислить число $inline$S (\tau)$inline$нумераций вершин дерева $inline$\tau$inline$ числами от 1 до $inline$n$inline$ таких, что для каждого ребра число в его верхней вершине больше чем в нижней. Одна из таких нумераций приведена на средней картинке. Ответ формулируется с помощью размеров крюков . Крюком $inline$H (v)$inline$ вершины $inline$v$inline$ назовём поддерево, растущее из этой вершины, а его размером просто число вершин в нём. Длины крюков написаны на правой картинке рядом с соответствующими вершинами. Так вот, число нумераций равно $inline$n!$inline$ делить на произведение размеров крюков, так для нашего примера
$$display$$S (\tau) = \, \frac{8!}{8\cdot 4 \cdot 3 \cdot 2\cdot 1 \cdot 1\cdot 1\cdot 1} = 210.$$display$$
Можно доказывать ту формулу по-разному, например индукцией по числу вершин, но наш взгляд на случайные перестановки позволяет провести доказательство вообще без вычислений. Оно лучше не только элегантностью, но и тем что хорошо обобщается на более тонкие вопросы о нумерациях с предписанными неравенствами, но об этом не сейчас. Так вот, возьмём n различных вещественных чисел и расставим их случайно в вершины дерева, в каждую по одному числу, все $inline$n!$inline$ перестановок равновероятны. Какова вероятность того, что для каждого ребра число в верхней вершине ребра больше числа в его нижней вершине? Ответ: $inline$S (\tau)/n!$inline$, и от набора чисел он не зависит. А раз не зависит, то давайте считать числа тоже выбранными случайно — для определённости, в отрезке $inline$[0,1]$inline$. Вместо того, чтобы сначала случайно выбирать числа, а потом случайно расставлять их в вершины дерева, мы можем просто случайно и независимо выбрать число в каждой вершине: их перестановка окажется случайной автоматически. Таким образом, $inline$S (\tau)/n!$inline$ это вероятность того, что для случайных независимых чисел $inline$\xi (v)$inline$, выбранных по одному для каждой вершины $inline$v$inline$ дерева $inline$\tau$inline$, выполняются все неравенства вида $inline$\xi (v)>\xi (u)$inline$ для всех рёбер $inline$v\to u$inline$, $inline$v$inline$ — верхняя вершина ребра, а $inline$u$inline$ — нижняя. Сформулируем эти условия в равносильном виде, но немного иначе: для каждой вершины $inline$v$inline$ должно происходить такое событие — обозначу его
$inline$Q (v)$inline$: число $inline$\xi (v)$inline$ — максимальное среди всех чисел в вершинах поддерева-крюка $inline$H (v)$inline$.
Заметим, что $inline$\frac{1}{|H (v)|}$inline$ это вероятность события $inline$Q (v)$inline$. В самом деле, в крюке $inline$H (v)$inline$ имеется $inline$|H (v)|$inline$ вершин и максимальное по крюку число сопоставлено каждой из них с равной вероятностью $inline$\frac{1}{|H (v)|}$inline$. Таким образом, формула крюков $inline$S (\tau)/n!=\prod_v \frac{1}{|H (v)|}$inline$ может быть сформулировано так: вероятность того, что происходят сразу все события $inline$Q (v)$inline$, равна произведению вероятностей этих событий. Причин на то может быть много разных, но тут работает первая, приходящая в голову: эти события независимы. Чтобы это понять, посмотрим, например, на событие $inline$Q (r)$inline$ (соответствующее корню). Оно состоит в том, что число в корне больше всех остальных чисел в вершинах, а прочие события касаются сравнений между собой чисел, написанных не в корне. То есть $inline$Q (r)$inline$ касается числа $inline$\xi (r)$inline$ и множества чисел в остальных вершинах, а все остальные события — порядка чисел в вершинах, отличных от корня. Как мы уже обсуждали, «порядок» и «множество» независимы, поэтому событие $inline$Q (r)$inline$ не зависит от прочих. Спускаясь далее по дереву, получим, что все эти события независимы, откуда и следует требуемое.
Обычно формулой крюков называют формулу для нумераций не вершин в дереве, а клеток в диаграмме Юнга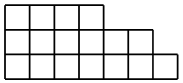
, возрастающих в направлениях координатных осей, и крюки там больше похоже на крюки чем для деревьев. Но эта формула доказывается сложнее и заслуживает отдельного поста.
Раз уж пришлось к слову, не могу не рассказать о модели случайной диаграммы Юнга. Диаграмма Юнга это вот такая фигура из $inline$n$inline$ единичных квадратиков, длины её строк возрастают снизу вверх, а длины столбцов слева направо. Количество диаграмм Юнга площади $inline$n$inline$ обозначается $inline$p (n)$inline$, эта важная функция ведёт себя интересно и необычно: например, она растёт быстрее любого многочлена, но медленнее любой экспоненты. Поэтому, в частности, генерировать случайную диаграмму Юнга (если мы хотим, чтобы все диаграммы площади $inline$n$inline$ имели равную вероятность $inline$1/p (n)$inline$) дело нетривиальное. Например, если добавлять клеточки по одной, выбирая место добавления случайно, разные диаграммы будут иметь разные вероятности (так, вероятность однострочечной диаграммы получается равной $inline$½^{n-1}$inline$.) Выходит занимательная мера на диаграммах, но не равномерная. Равномерную можно получить так. Возьмём число $inline$t\in (0,1)$inline$, для наших целей лучше всего годятся числа в районе $inline$1-\mathrm{const}/\sqrt{n}$inline$. Для каждого $inline$k=1,2,\ldots$inline$
рассмотрим геометрическое распределение на целых неотрицательных числах со средним $inline$t^k$inline$ (то есть вероятность числа $inline$m=0,1,\ldots$inline$ равна $inline$t^{km}(1-t^k)$inline$). Выберем согласно нему случайную величину $inline$m_k$inline$ (есть много способов как это организовать). При больших $inline$k$inline$ скорее всего 0. Посмотрим на диаграмму Юнга, в которой $inline$m_k$inline$ строк имеют длину $inline$k$inline$ при каждом $inline$k=1,2,\ldots $inline$. Я называю это методом кораблей, потому что общая площадь иногда равна $inline$n$inline$. Если не равна, то повторяем эксперимент. На самом деле равна $inline$n$inline$ она достаточно часто, если умно выбрать $inline$t\in (0,1)$inline$. Предлагаю читателю самостоятельно доказать, что все диаграммы данной площади равновероятны и оценить число шагов.
