[Из песочницы] SamsPcbGuide, часть 1: Оценка индуктивности элементов топологии печатных плат
Предисловие
В поисках ответов на вопросы, возникающие при проектировании печатных плат, мною был изучен значительный объём литературы — как больших монографий, так и отдельных технических статей. За исключением, наверное, нескольких статей, это была англоязычная литература. Я подумал, а почему бы не оформить накопившийся опыт в виде практического руководства, которое может оказаться полезным как начинающим, так и, надеюсь, более опытным отечественным разработчикам. Начиная, я думал о распространении ценной информации, а краем мысли и о вкладе в отрасль в целом. Настоящая публикация открывает целую серию статей, в которых с практической точки зрения будут рассмотрены основные задачи, возникающие при разработке печатных плат, и в систематизированном виде изложены ключевые рекомендации с обязательным указанием их физических основ и условий применимости.Последние два фактора очень важны, так как рекомендация отдельно, сама по себе может принести вреда больше, чем пользы. В условиях ускорения вывода радиоэлектронной продукции на рынок производители микросхем стремятся дать потребителю готовые решения в виде отладочных и оценочных плат, инструкций в документации, а также выпускают руководства, содержащие набор рекомендаций разработчикам с краткими пояснениями (например, [1] от Texas Instruments). Эти рекомендации перетекают из руководства в руководство, теряя свои основы и границы применимости и в итоге, как говорится в одной из статей [2] на сайте LearnEMC:
Худшие печатные платы, что нам доводилось видеть, были разработаны инженерами, которые пытались обеспечить соответствие всем пунктам списка рекомендаций по повышению ЭМС печатных плат.
Ряд рекомендаций противоречит друг другу, а некоторые продолжают использоваться, несмотря на то, что они устарели. Вот почему я призываю экспертное сообщество к обсуждению, обратной связи как положительной, так и отрицательной, к конструктивной критике, основанной на реальном опыте проектирования печатных плат. С одной общей максималистской целью — докопаться до истины, до базовых практических принципов.
Индуктивность и электромагнитная индукция
Первая публикация не случайно посвящена индуктивности. Понимание физических основ индуктивности критически важно, так как с индуктивностью (а точнее, с паразитной индуктивностью) топологии печатной платы связаны многие проблемы ЭМИ и ЭМС, о которых будет говориться в последующих статьях цикла. О сложности вопроса можно судить по нечёткой терминологии, когда одним термином «индуктивность» называют величины хоть и связанные, но имеющие совершенно разный математический и физический смысл: индуктивность выводов корпуса, индуктивность катушки, паразитная индуктивность конденсатора ESL, индуктивность петли и т.п.
Согласно классическому определению [3] индуктивность — это коэффициент пропорциональности между силой постоянного тока в тонком замкнутом проводящем контуре и магнитным потоком через этот контур. Первое, на что необходимо обратить внимание, — индуктивность определена для замкнутого контура. В определении также говорится о полном магнитном потоке, разберёмся с ним. Движущийся электрический заряд порождает магнитное поле, а магнитное поле вокруг электрического тока — суперпозиция (векторная сумма) магнитных полей отдельных зарядов. Для наглядного изображения магнитных полей используются силовые линии. Направление касательной к силовой линии в каждой точке совпадает с направлением вектора магнитного поля в этой точке. Например, для тока в длинном прямолинейном проводе силовые линии — это концентрические окружности, плоскость которых перпендикулярна проводу, а направление определяется известным «правилом правой руки» (рис. 1). С помощью силовых линий можно судить и об относительной напряжённости магнитного поля — она тем выше, чем выше плотность силовых линий (число линий через единицу перпендикулярной им площади). Далее, поток магнитного поля $inline$B$inline$ — это поверхностный интеграл напряжённости магнитного поля $inline$Ф_B = \oint\limits_S\vec{B}d\vec{S}$inline$, где поверхность $inline$S$inline$ определяется контуром тока. Следовательно, поток магнитного поля пропорционален числу силовых линий магнитного поля через поверхность $inline$S$inline$ и определение индуктивности можно привести к более удобному с практической точки зрения виду:
Индуктивность пропорциональна числу силовых линий магнитного поля, которые пересекают поверхность, определяемую контуром тока, при величине тока в 1 А.

Изменение силы тока приводит к пропорциональному изменению напряжённости магнитного поля, которое условно можно представить как изменение количества силовых линий вокруг проводника. Такой подход к пониманию индуктивности, описанный Эриком Богатиным [4, 5], был подвергнут аргументированной критике со стороны не менее авторитетного автора, Клэйтона Пола [6, 7]. Действительно, силовые линии — это абстракция и никто не определяет индуктивность с помощью подсчёта их количества (которое, очевидно, бесконечно). Однако такое наглядное представление упрощает понимание многих закономерностей, связанных с магнитным полем. В то время как теоретическая физика стремится к поиску универсального уравнения, описывающего все взаимодействия, для практических целей ищутся приближённые аналитические соотношения, обладающие невысокой вычислительной сложностью. На практике никто не начинает анализ электрической цепи с составления уравнений Максвелла для её участков. Даже несмотря на появление САПР, снимающих вопрос вычислительной сложности, необходимость упрощённых соотношений сохраняется, так как они дают качественное понимание основных закономерностей и позволяют выполнять первоначальные оценочные инженерные расчёты.
Следует сделать одно важное замечание: индуктивность не зависит от величины тока и определяется конфигурацией линий тока в проводнике. Часто в подобной формулировке говорится об определяющем значении геометрии проводника, но такая формулировка не учитывает тот эффект, что распределение тока в проводнике не всегда равномерное — на него влияет частота тока (скин-эффект) и близость других проводников с током. Наиболее простой для получения аналитических соотношений случай — это равномерное распределение тока по сечению проводника и все известные аналитическое соотношения получены с учётом этого предположения. На практике указанные эффекты мало влияют на значение индуктивности и использование этих формул расчёта индуктивности обеспечивает достаточную для практических задач точность.
Рассмотрим физическое явление, связанное с индуктивностью, которое и определяет её основополагающую роль в вопросах ЭМС и ЭМИ. Открыто оно Майклом Фарадеем и носит название электромагнитной индукции. Согласно одноимённому закону, при изменении потока магнитного поля Φ_B через замкнутый контур в нём возникает ЭДС $inline$V = -\frac{dФ_В}{dt}$inline$. В терминах силовых линий это означает (помним об условности этого подхода):
Изменение количества силовых линий через замкнутый контур приводит к возникновению в нём напряжения ЭДС.
Изменение это может быть вызвано любой из причин: изменение силы тока в самом проводнике, изменение силы тока в соседнем проводнике, изменение геометрии контура или его ориентации в магнитном поле, нахождение контура в переменном магнитном поле, изменение расстояния до другого контура с током и т.п.
Частичная индуктивность — удобный инструмент
Прежде чем перейти к формулам, проведём разграничение между разными типами «индуктивностей» и уточним терминологию (рис. 2). Если рассчитывается магнитный поток через контур, вызванный только током в самом контуре, то говорят о собственной индуктивности контура L (англ. loop inductance, self-inductance). Если учитывается магнитный поток через контур, вызванный только током в другом контуре, то это взаимная индуктивность контуров M (англ. loop mutual inductance, mutual inductance). С практической точки зрения важен вопрос, чему равно напряжение ЭДС индукции на конкретном участке контура электрической цепи. Но для этого нужно связать с этим участком значение индуктивности, а индуктивность контура в этом смысле неделима. Поэтому был разработан математический аппарат расчёта частичной собственной индуктивности участка контура $inline$L^P$inline$ (англ. partial self-inductance) и частичной взаимной индуктивности двух участков одного или разных контуров $inline$M^P$inline$ (англ. partial mutual inductance). Они рассчитываются так, что учитывается магнитное поле, вызванное только током этого участка, словно остальная часть контура не существует. Иначе это можно представить следующим образом — остальная часть контура замещается бесконечно длинными подводящим проводами и контур, через который вычисляется магнитный поток, определяется так, как на рис. 2.

Зная значения частичных собственных и взаимных индуктивностей отдельных участков контура может быть получено значение индуктивности любой их комбинации, в том числе и всего контура:
$$display$$L = \sum_i L^P_i + \sum_{i \ne j} M^P_{ij}$$display$$
здесь $inline$L_i^P$inline$ — собственная индуктивность i-го участка, $inline$M_{ij}^P$inline$ — взаимная индуктивность i-го и j-го участков, знак которой положителен, если токи в участках сонаправлены и отрицателен в противном случае. Взаимная индуктивность обладает свойством симметрии, то есть $inline$M_{ij}^P = M_{ji}^P$inline$, для участков, перпендикулярных друг другу, взаимная индуктивность равна нулю. Если в расчёте учитывается только ток рассматриваемого составного участка, то указанная формула даёт его частичную индуктивность, если же во второй сумме учитывается влияние всего контура, то полученное значение — полная индуктивность участка (англ. total inductance, net inductance) (рис. 3).

Именно полная индуктивность определяет падение напряжение на участке при изменении тока I в контуре $inline$V = -L^{NET}\frac{dI}{dt}$inline$. Из формулы для полной индуктивности участка прямоугольного контура $inline$L_1^{NET}$inline$ на рис. 3 видно, что это значение тем меньше, чем больше взаимная индуктивность этого участка с противоположным ему $inline$M_{13}^P$inline$. Именно поэтому сближение сигнальной дорожки и опорного слоя рекомендуется как мера снижения шумов в опорном слое.
Частичная индуктивность параллельного соединения двух участков рассчитывается по формуле:
$$display$$L_{i\|j}^P=\frac{L_i^PL_j^P-{M_{ij}^P}^2}{L_i^P+L_j^P-2M_{ij}^P},$$display$$
которая только в случае, когда взаимная индуктивность пренебрежимо мала (значительно удалённые проводники), превращается в известную формулу для параллельного соединения катушек индуктивности. В случае идентичных проводников (например, два одинаковых переходных отверстия) формула принимает вид
$$display$$L_i^P=L_j^P \Rightarrow L_{i\|j}^P=\frac{L_i^P+M_{ij}^P}{2},$$display$$
то есть индуктивность уменьшается в два раза только для проводников, расстояние между которыми достаточно велико, чтобы пренебречь их взаимной индуктивностью.
Расчётные формулы
В таблице 1 на схематических изображениях стрелкой указано направление тока, распределение которого равномерно по сечению. Так как именно распределение тока определяет индуктивность, важно соотносить распределение тока в рассматриваемой структуре печатной платы с указанной в таблице. Другим условием применимости формул, о котором нельзя забывать, является требование малости характерных размеров проводника l по сравнению с длиной волны λ (по крайней мере, l
Таблица 1. Формулы для оценки индуктивности элементов топологии печатной платы1.
Примечания к таблице 1:
1. Для среды с относительной магнитной проницаемостью μr = 1.
2. В расчёте на единицу длины.
3. Формула иногда применяется для оценки собственной индуктивности переходного отверстия между двумя сплошными слоями в предположении, что возвратный ток смещения равномерно распределён вокруг отверстия.
4. Формула может применяться для оценки собственной индуктивности пары переходных отверстий (например, обеспечивающих соединение блокировочного конденсатора).
5. Формула может применяться для оценки собственной индуктивности переходного отверстия.
6. Формула может применяться для оценки взаимной индуктивности параллельных переходных отверстий.
7. Габариты сплошных проводящих слоёв должны быть достаточно велики, чтобы не ограничивать распределение тока между переходными отверстиями.
Примеры
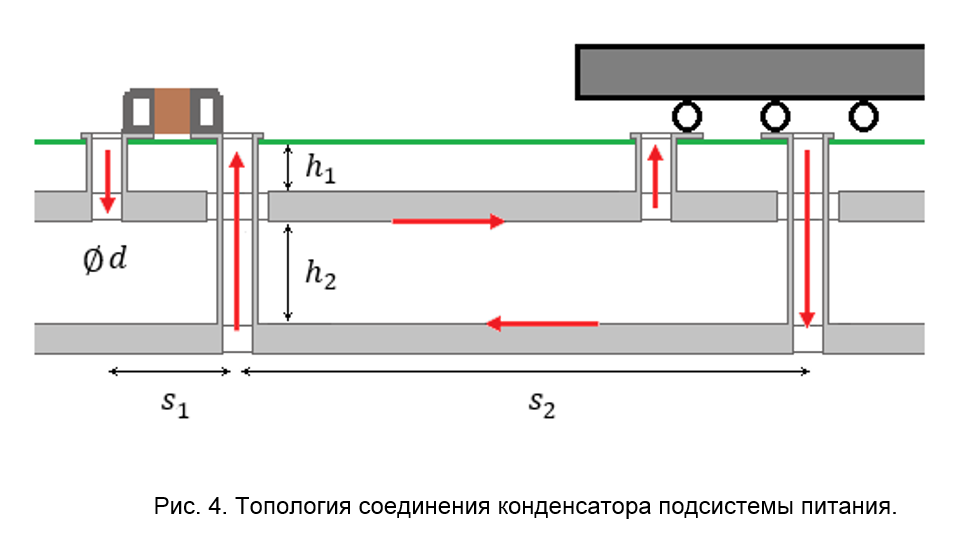
С использованием математического аппарата частичной индуктивности участков цепи и приведённых приближённых аналитических формул можно проводить оценку индуктивности участков топологии печатной платы и варьировать их геометрические параметры для снижения паразитной индуктивности. А следовательно, снижения искажений сигнала, шумов и ЭМИ — вопросов, которые будут рассматриваться в последующих статьях цикла. Полезно также произвести расчёт для типовых применяемых элементов топологии печатной платы, чтобы в дальнейшем при трассировке с ними ассоциировалось оценочное значение паразитной индуктивности. Для примера в таблице 2 представлены значения паразитной индуктивности элементов топологии соединения конденсатора подсистемы питания при различных параметрах геометрии (рис. 4).

Литература
[1] PCB Design Guidelines For Reduced EMI. Texas Instruments, 1999.
[2] Why You Should Be Cautious about Using EMC Design Rules. LearnEMC, 2017.
[3] Сивухин Д.В. Общий курс физики. Т. III. Электричество. Изд. 4-е. М.: Физматлит, 2004.
[4] Bogatin E. What is Inductance? Printed Circuit Design & Manufacture, 2007.
[5] Bogatin E. Signal and power integrity — simplified. 2 nd ed. Pearson, 2004.
[6] Paul C.R. What Do We Mean By «Inductance»? Part I: Loop Inductance. IEEE Practical Papers, 2007.
[7] Paul C.R. Inductance: loop and partial. Wiley, 2010.
Статья была впервые опубликована в журнале «Компоненты и технологии» 2017, №11. Публикация на «Geektimes» согласована с редакцией журнала.
