[Из песочницы] Решение разреженных СЛАУ больших размерностей средствами ManagedCuda в .NET23.06.2015 21:18

Зачастую в прикладных математических и компьютерных моделях возникает необходимость решать системы линейных алгебраических уравнений (СЛАУ). Как правило, на практике матрица в таких СЛАУ оказывается разреженной. Например, разреженные матрицы встречаются в моделях с конечно-разностными или конечно-элементными методами решения дифференциальных уравнений. Возникают сильно разреженные матрицы большой размерности при моделировании материальных и информационных потоков в крупных технологических сетях (системы газоснабжения и газораспределения, канализационные и теплоснабжающие системы, электросети и компьютерные сети и др.). Общим для технологических сетей является представление их моделей в виде графа, у которого матрица инциденций оказывается практически всегда сильно разреженной.

В статье будет рассказано о том, как ваш покорный слуга значительно повысил эффективность компьютерной модели расчета нестационарных течений газа в крупных системах газоснабжения произвольной конфигурации, благодаря применения библиотеки ManagedCuda и nVidia CUDA 7.0. Однако изложение будет вестись без привязки к конкретной предметной области.

Постановка задачи

Рассматривается классическая задача решения СЛАУ:
Ax=b
Здесь матрица A размером nxn, x — вектор неизвестных размером n, b — вектор известных свободных членов размером n.

Автор статьи занимается разработкой специализированного программно-вычислительного комплекса (ПВК) для моделирования и оптимизации нестационарных течений газа в системах газоснабжения. В решаемых мною задачах A является положительно определенным якобианом с диагональным преобладанием некоторой системы нелинейных уравнений. A получается в результате матричных преобразований матрицы инциденций графа системы газоснабжения и других матриц. В моих практических расчетах A обычно заполнена на 6–10%, остальное нули. Размер же ее зависит от размера конкретной системы газоснабжения и варьируется n от 10 до 1000.

Наш ПВК разрабатывается под .NET 4.0 на C#. Расчетный модуль и вся математика также разрабатывается на C#. Изначально для решения СЛАУ я написал собственную, доморощенную, библиотеку, не использующую технологию разреженных матриц. Для решения СЛАУ применял метод LU декомпозиции. И до поры меня все устраивало, пока я не начал заниматься задачей оптимизацией нестационарных режимов течения газа, где приходится методом динамического программирования осуществлять большое количество переборов значений управляющих параметров и, соответственно, много раз решать СЛАУ. Стандартный профилировщик Visual Studio показал, что в процессе выполнения программы около 40% затрат приходится на решение СЛАУ.

Именно в этот момент я понял, что пора что-то менять.

Математическая библиотека Math.Net Numerics

Проведя анализ имеющихся математических библиотек под .Net я решил остановиться на библиотеке Math.Net Numerics. Подробно ознакомиться с ней вы можете здесь.

Меня заинтересовали ее ключевые возможности:

Реализована технология разреженные матриц и векторов;
Имеются встроенные все необходимые вектор-матричные операции;
Присутствуют встроенные решатели;
Интуитивно понятный API.

Приведу листинг с примером решения СЛАУ средствами Math.Net Numerics:

SparseMatrix matrix = new SparseMatrix(n);
double[] rightSide = new double[n];
//Заполнение матрицы и вектора правой части
//...
var x = matrix.Solve(DenseVector.Build.DenseOfArray(rightSide)).ToArray();

Как видно, все очень элегантно выглядит, но практически сразу меня настигло разочарование — встроенный решатель Math.Net Numerics работал значительно медленнее моего. Меня это совершенно не устроило, однако претензии к реализованным в библиотеке вектор-матричным операциям не столь существенные. Поэтому полностью отказываться от Math.Net Numerics я не стал, оставив код, где производится работа с векторами и матрицами.

Но тут мне вспомнился весьма удачный опыт коллег по аспирантуре, которые для решения задач подземной гидродинамики использовали графические процессоры. В распоряжении у меня имеется ноутбук с видеокартой nVidia GeeForce GT 540M с 2 GB памяти и поддержкой технологии CUDA. Было принято решение попробовать эту технологию на деле, о чем теперь не жалею.

Библиотека ManagedCuda

О технологии CUDA на этом сайте имеется большое количество материала, поэтому любопытный читатель без особого труда его найдет. Я же остановлюсь на том, как решал поставленную перед собой задачу.

Меня заинтересовала библиотека cuSPARSE. При первом знакомстве с ней я наткнулся на проблемы:

Непосредственная работа с библиотекой возможна только через C/C++. Конечно, проблема решится, если использовать качественный враппер, который очень не хотелось писать. По результатам поиска был найден CUDA-враппер для .Net под названием Cudafy.
cuSPARCE позволяет решать СЛАУ с треугольными матрицами, а в моем случае матрицы таковыми не являются. Однако cuSPARSE содержит методы факторизации матриц, приводящие их к треугольной форме (метод LU факторизации, разложение Холецкого). Однако в API Cudafy отсутствовали соответствующие методы, поэтому от Cudafy пришлось отказаться.

После продолжения поиска я открыл для себя библиотеку ManagedCuda, которая является высокоуровневой оберткой над CUDA API. Все её возможности я перечислять не буду — их можно найти на официальном сайте, но остановлюсь на том, как можно, используя Math.Net Numerics и ManagedCuda, элегантно и эффективно решать СЛАУ.

Идея заключается в использовании SparseMatrix из Math.Net Numerics для формирования и хранения разреженной матрицы в формате CSR, который принимают на вход cuSPARSE и ManagedCuda. Далее приводится листинг соответствующей программы:

SparseMatrix matrix = new SparseMatrix(n);
double[] rightSide = new double[n];
//Заполнение матрицы и вектора правой части
//...

var storage = matrix.Storage as SparseCompressedRowMatrixStorage; //Содержит необходимую 
//информацию о разреженной матрице в CSR формате

var nonZeroValues = storage.EnumerateNonZero().ToArray(); //Получаем ненулевые элементы матрицы
double[] x = new double[matrix.RowCount]; //Выделяется память под результат расчета

CudaSolveSparse sp = new CudaSolveSparse(); //Создаем решатель из библиотеки ManagedCuda
CudaSparseMatrixDescriptor matrixDescriptor = new CudaSparseMatrixDescriptor(); // Создается дескриптор матрицы
double tolerance = 0.00001; //Точность расчета. Значение взято для иллюстрации

sp.CsrlsvluHost(matrix.RowCount, nonZeroValues.Length, matrixDescriptor, nonZeroValues, 
    storage.RowPointers, storage.ColumnIndices, rightSide,
    tolerance, 0, x); //Решение СЛАУ методом LU факторизации

Вычислительный эксперимент: анализ временных затрат на решению СЛАУ различными технологиями

Дабы не утомлять читателя сухим текстом и листингами программ, рассмотрим результаты расчетов СЛАУ размерностей от 50 до 500 с помощью различных технологий:

Доморощенный решатель, написанный автором статьи. Назовем его Mani.Net.
Стандартный решатель библиотеки Math.Net Numerics.
Метод LU декомпозиции библиотеки ManagedCuda.

Матрица A заполняется на 10% случайным образом.

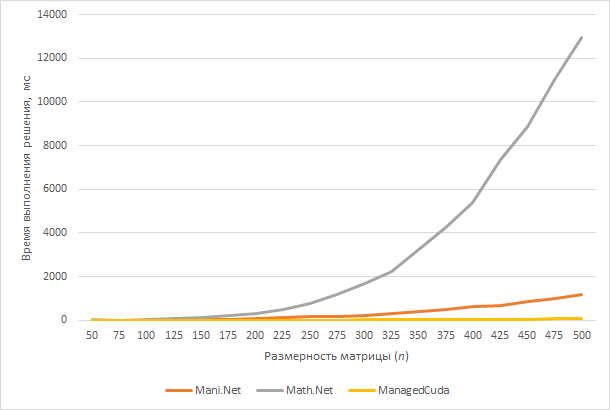
Рисунок наглядно демонстрирует, почему мне пришлось отказаться от Math.Net Numerics для решения СЛАУ.
Отметим, при размерности матрицы равной 500 моему собственному решателю (Mani.Net) потребовалось 1170 мс, Math.Net Numerics — 12968 мс, ManagedCuda — 70 мс.

Заключение

Следует ожидать в комментариях замечания, мол де не на всех машинах есть GPU nVidia с поддержкой CUDA. Действительно, это так. Поэтому наше приложение настроено на две конфигурации компиляции: с собственной библиотекой решения СЛАУ и с ManagedCuda.

Насчет Mani.Net отмечу, что это не реклама моей собственной библиотеки. Найти ее нигде невозможно и никому её я передавать не буду. Нет, я не жадный. Мне стыдно за код.

Спасибо за прочтение статьи! Буду рад узнать о вашем мнении и замечаниях в комментариях.