[Из песочницы] Python и теория множеств27.08.2020 18:17

В Python есть очень полезный тип данных для работы с множествами — это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.

Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.

Множество

Множество — это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:

Множество — это не более чем неупорядоченная коллекция уникальных элементов.

Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.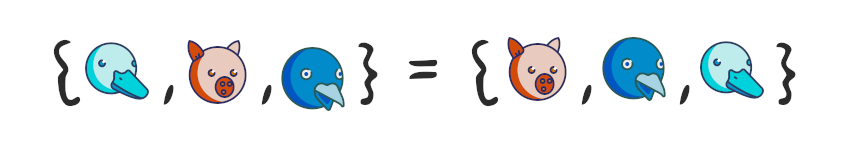

Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.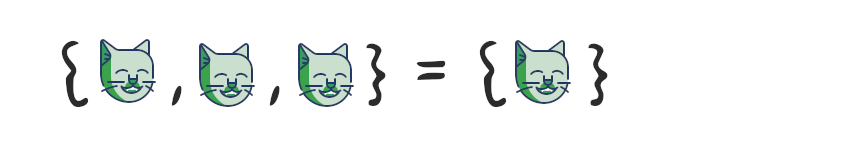

Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества — бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.

Множества в Python

Множество в Python можно создать несколькими способами. Самый простой — это задать множество перечислением его элементов в фигурных скобках:

fruits = {"banana", "apple", "orange"}

Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:

wrong_empty_set = {}
print(type(wrong_empty_set))

# Вывод

Для создания пустого множества нужно непосредственно использовать set():

correct_empty_set = set()
print(type(correct_empty_set))

# Вывод

Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):

color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)

# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}

Ещё одна возможность создания множества — это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).

numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]

# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
    number for number in numbers
    if number % 2 == 0
}
print(even_numbers)

# Вывод (порядок может быть другим):
{2, 4, 6}

Хешируемые объекты

Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари — это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) — хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.

# Множество кортежей (tuple)
records = {
    ("Москва", 17_200_000), 
    ("Санкт-Петербург", 5_400_000), 
    ("Новосибирск", 1_600_000),
    ("Москва", 17_200_000),
}

for city, population in records:
    print(city)

# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-Петербург

Объекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.

class City:
    def __init__(self, name: str):
        self.name = name

    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self.name}")'

print(City("Moscow") == City("Moscow"))

# Вывод:
False

cities = {City("Moscow"), City("Moscow")}
print(cities)

# Вывод
{City("Moscow"), City("Moscow")}

Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:

class City:
    def __init__(self, name: str):
        # Атрибут name не должен изменяться, пока объект существует
        # Для простоты пометим этот атрибут как внутренний
        self._name = name

    def __hash__(self) -> int:
        """ Хеш от объекта
        """
        return hash((self._name, self.__class__))

    def __eq__(self, other) -> bool:
        """ Определяем семантику равентсва (оператор ==)
        """
        if not isinstance(other, self.__class__):
            return False
        return self._name == other._name

    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self._name}")'

Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:

• Хеш объекта не должен изменяться, пока этот объект существует
• Равные объекты должны возвращать одинаковый хеш

moscow = City("Moscow")
moscow_again = City("Moscow")

print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True

# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)

# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}

Свойства множеств

Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:

• Определена операция проверки принадлежности элемента множеству
• Можно получить количество элементов в множестве
• Множества являются iterable-объектами

Принадлежность множеству

Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.

tremendously_huge_set = {"red", "green", "blue"}

if "green" in tremendously_huge_set:
    print("Green is there!")
else:
    print("Unfortunately, there is no green...")

# Вывод:
Green is there!

if "purple" in tremendously_huge_set:
    print("Purple is there!")
else:
    print("Unfortunately, there is no purple...")

# Вывод:
Unfortunately, there is no purple...

Мощность множества

Мощность множества — это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.

even_numbers = {i for i in range(100) if i % 2 == 0}

# Мощность множества
cardinality = len(even_numbers)
print(cardinality)

# Вывод:
50

Перебор элементов множества

Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.

colors = {"red", "green", "blue"}

# Элементы множества можно перебрать с помощью цикла for
for color in colors:
    print(color)

# Вывод (порядок может быть другим):
red
green
blue

# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)

# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}

Отношения между множествами

Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.

Равные множества

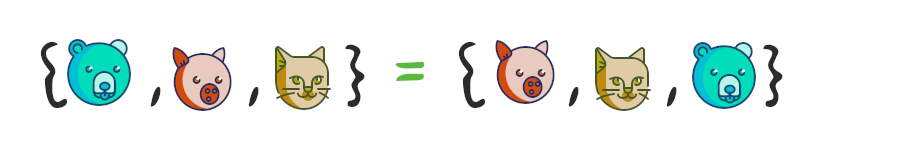
Тут всё довольно просто — два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.

my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)

# Вывод:
True

Непересекающиеся множества

Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.

even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}

# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
    print("Множества не пересекаются!")

# Вывод:
Множества не пересекаются!

Подмножество и надмножество

Подмножество множества S — это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.

# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}

# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))

# Множество чисел Фибоначчи является подмножеством множества 
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
    print("Подмножество!")

# Вывод:
Подмножество!

# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers.issuperset(fibonacci_numbers):
    print("Надмножество!")

# Вывод:
Надмножество!

Пустое множество является подмножеством абсолютно любого множества.

empty = set()

# Методы issubset и issuperset могут принимать любой iterable-объект
print(
    empty.issubset(range(100))
    and empty.issubset(["red", "green", "blue"])
    and empty.issubset(set())
)

# Вывод:
True

Само множество является подмножеством самого себя.

natural_numbers = set(range(100))

if natural_numbers.issubset(natural_numbers):
    print("Подмножество!")

# Вывод:
Подмножество!

Операции над множествами

Рассмотрим основные операции, опредяляемые над множествами.

Объединение множеств

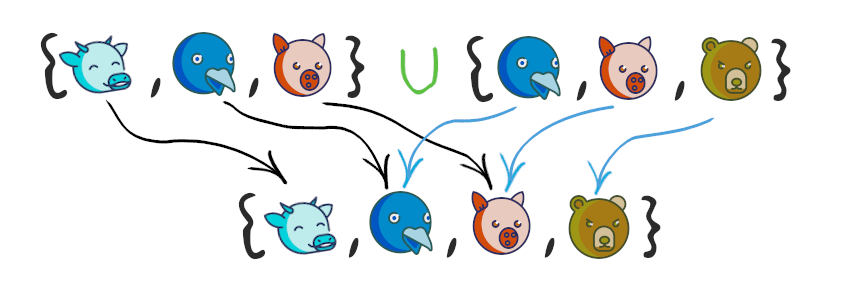
Объединение множеств — это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.

my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}

# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)

# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}

# Также можно использовать ментод union.
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)

# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}

Добавление элементов в множество

Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).

colors = {"red", "green", "blue"}

# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)

# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}

# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers.update(i**2 for i in [1, 2, 3])
print(numbers)

# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}

Пересечение множеств

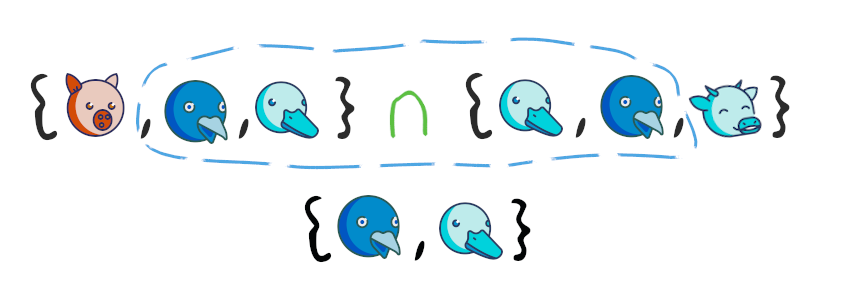
Пересечение множеств — это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.

def is_prime(number: int) -> bool:
    """ Возвращает True, если number - это простое число
    """
    assert number > 1
    return all(number % i for i in range(2, int(number**0.5) + 1))

def is_fibonacci(number: int) -> bool:
    """ Возвращает True, если number - это число Фибоначчи
    """
    assert number > 1
    a, b = 0, 1
    while a + b < number:
        a, b = b, a + b
    return a + b == number

# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))

# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))

# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)

# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes

print(prime_fibonacci)

# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}

При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.

Разность множеств

Разность двух множеств — это множество, в которое входят все элементы первого множества, не входящие во второе множество.

i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
    "Go": 0.4, 
    "C++": 0.6, 
    "Rust": 0.2, 
    "Java": 0.9
}

# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)

# Вывод (порядок может быть другим):
{"Rust", "C++"}

# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)

# Вывод:
{"Python"}

Удаление элементов из множества

Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент — это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).

fruits = {"apple", "orange", "banana"}

# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)

# Вывод (порядок может быть другим):
{"apple", "banana"}

# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple")  # KeyError: "pineapple"

Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.

numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers.difference_update(even_numbers_under_100)
print(numbers)

# Вывод (порядок может быть другим):
{1, 3, 5, 7, 9}

Симметрическая разность множеств

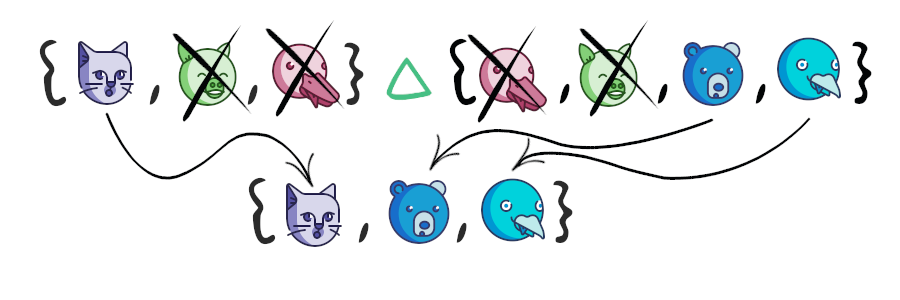
Симметрическая разность множеств — это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Также симметрическую разность можно рассматривать как разность между объединением и пересечением исходных множеств.

non_positive = {-3, -2, -1, 0}
non_negative = {0, 1, 2, 3}

# Обратите внимание, что оператор `^` может применяться
# только для объектов типа set
non_zero = non_positive ^ non_negative
print(non_zero)

# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}

Как видно из примера выше, число 0 принадлежит обоим исходным множествам, и поэтому оно не входит в результирующее множество. Для операции симметрической разности, помимо оператора ^, также существует два специальных метода — symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.

non_positive = {-3, -2, -1, 0}
non_negative = range(4)

non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)

# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}

# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)

# Вывод (порядок может быть другим):
{"red", "yellow"}

Заключение

Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.

Полезные ссылки

Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness

© Habrahabr.ru