[Из песочницы] Построение функций в консоли. Часть 1

У большинства наверняка возникнет резонный вопрос: зачем?
С прагматической точки зрения незачем) Всегда можно воспользоваться условным Вольфрамом, а если нужно это сделать в питоне, то использовать специальные модули, которыми не так уж и сложно овладеть.
Но если вдруг вам дали такое задание или вы просто очень любите программирование, как я, то вам предстоят увлекательные —, а временами и не очень — часы написания программы и ее отладки)
При написании сия шедевра нам очень как понадобится пошаговая отладка, поэтому, пожалуйста, скачайте себе PyCharm, VS или что-то еще с такой возможностью. Для построения таблиц отсутствие этой функции еще не так критично, а вот для построения графика…
Итак, в чем будет заключаться моя программа. На вход она будет принимать три значения: начало и конец отрезка, на котором мы хотим увидеть нашу функцию и шаг, с которым мы будем двигаться. Дальше мы нарисуем таблицу значений функции в каждой точке из заданного входными данными диапазона значений. Ну, а затем будем рисовать сам график функции с подвижной осью y.
Итак, поехали
Для начала я объявлю несколько функций, значения которых мы будем считать. Специально возьму довольно простые
from math import sqrt
def y1(x):
return x**3 - 2*x**2 + 4*x - 8
def y2(x):
return 1 - 1/x**2
def y3(x):
return sqrt(abs(y1(x)*y2(x)))
Теперь у нас есть три функции, две из которых имеют точку разрыва. Из модуля math, в котором хранятся все математические плюшки (в том числе и косинусы, арктангенсы и прочая тригонометрия) импортируем sqrt, то есть квадратный корень. Он нам нужен для того, чтобы считать функцию y3.
После этого нам нужно считать диапазон функции по икс и шаг, с которым мы пройдемся по этому диапазону. Для этого я буду использовать map.
В качестве первого параметра эта функция принимает какую-то функцию, которая как-то преобразует необходимые нам данные, а в качестве второго аргумента — какой-то лист данных, который нам требуется обработать
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\
" x-coordinates and a pace dividing them by a"\
" space:").split())
Считываем три значения, введенные через пробел, разделяем их на элементы по пробелу (при помощи метода split, который при вызове без параметров автоматически будет разделять указанную вами строку по пробелам). Данные, введенные при помощи input (), по умолчанию будет типа str, то есть строкой, поэтому никаких ошибок здесь у нас не возникнет.
Так как числа-границы диапазона могут быть дробными, каждый элемент полученного массива мы конвертируем в действительное число при помощи функции float.
Отмечу, что переменные объявляются без указания типа данных. Он определяется автоматически (тип данных значения, которое вы пытаетесь присвоить переменной), либо при помощи функций str, int, float и т.д. задаются переменным вручную, применяя эти самые функции к значениям. Одна и та же переменная в течение всей программы может иметь разный тип данных — для этого достаточно присвоить ей новое значение с другим типом данных
Например,
auxiliary_variable = "строка" #переменная имеет тип str
auxiliary_variable = 2 #переменная имеет тип int
auxiliary_variable = 9.218 #переменная имеет тип float
Вернемся к нашей программе. Нам нужно проверить, корректны ли введенные данные.
Программа должна печатать, что введенные данные неправильные, если:
- шаг равен 0
- введенная нижняя граница диапазона больше верхней, а шаг положительный (то есть у нас есть арифметическая прогрессия вида xn = from_x + pace_x*(n — 1), в которой from_x > to_x. Так как pace_x > 0, то эта прогрессия будет возрастающей и мы никогда не дойдем до to_x)
- введенная нижняя граница диапазона меньше верхней, а шаг отрицательный (аналогичные рассуждения)
- графики, состоящие из одной точки не информативны, поэтому отрезок, на котором мы строим функцию, должен содержать хотя бы два значения
Сформулируем эти условия в код. Очевидно, что первый пункт задать легко. Второй и третий можно объединить в один, если заметить, что знак разницы между первым (from_x) и последним (to_x) должен совпадать со знаком шага. Ну и четвертый пункт тоже не так уж и сложен: модуль разницы первого и последнего значения должен быть не меньше, чем модуль шага.
Из-за модуля у нас может возникнуть ситуация, при которой знаки разницы и шага не будут совпадать, но второе условие отсечет эти случаи, поэтому условие корректно.
В итоге эти три условия будут выглядеть так:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
#какой-то код
else:
print("Incorrect input")
Перейдем непосредственно к таблице. Для простоты отладки я создам несколько переменных с говорящими названиями, которые будут отвечать за точность чисел, количество пробелов до числа, количество пробелов после числа и т.д.
dials_precision = "%10.6g" # точность числа
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
delimiter = ' '
is_sequence_decreasing = to_x - from_x < 0
min_y1_value, max_y1_value, x_copy = y1(from_x), y1(from_x), from_x
negative_value_exists = False
Итак, что здесь происходит?

dials_precision = "%10.6g" # точность числа
в этой строке я задаю точность числа. Максимум 10 знаков на все число и 6 знаков на дробную часть. Если у нас будет слишком большое для этого диапазона значение, то будут появляться всякие е-15 или что-то подобное.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision является строкой, поэтому мы можем взять срез этой строки, то есть какую-то подстроку. В данном случае нам нужно получить цифру 10, поэтому берем символы под 1 и 2 индексами, эту подстроку приводим к целочисленному типу данных, делим на два и округляем в меньшую сторону.
Эта переменная нужна нам для того, чтобы в заголовке таблицы надписи были выровнены по центру ячейки
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
как можно понять по названию, эта переменная отвечает за длину нижних границ ячеек таблицы значений функции. Всего число у нас занимает 10 позиций, значит столбец не может быть шириной менее 10. Когда у нас возникают числа с форматом e-15 (описано выше), то значение занимает 11–12 позиций. Поэтому к 10 мы добавляем еще двойку.
4 отвечает за количество столбцов (x, y1, y2, y3), а 5 — за количество символов, ограничивающих ячейку, в строке.
Остальные переменные вроде бы интуитивно понятны, поэтому переходим к печати таблички
print("|" + (spaces_in_the_title + 1) * delimiter + 'x'
+ spaces_in_the_title * delimiter + '|' +
spaces_in_the_title * delimiter + "y1" +\
spaces_in_the_title* delimiter\
+ '|' + spaces_in_the_title * delimiter + 'y2'\
+ spaces_in_the_title * delimiter + '|' +\
spaces_in_the_title * delimiter\
+ "y3" + spaces_in_the_title * delimiter + "|\n"\
+ length_of_table_lower_bound * '-')
если соединить весь код, который мы уже написали, то в консоли мы увидим вот это:
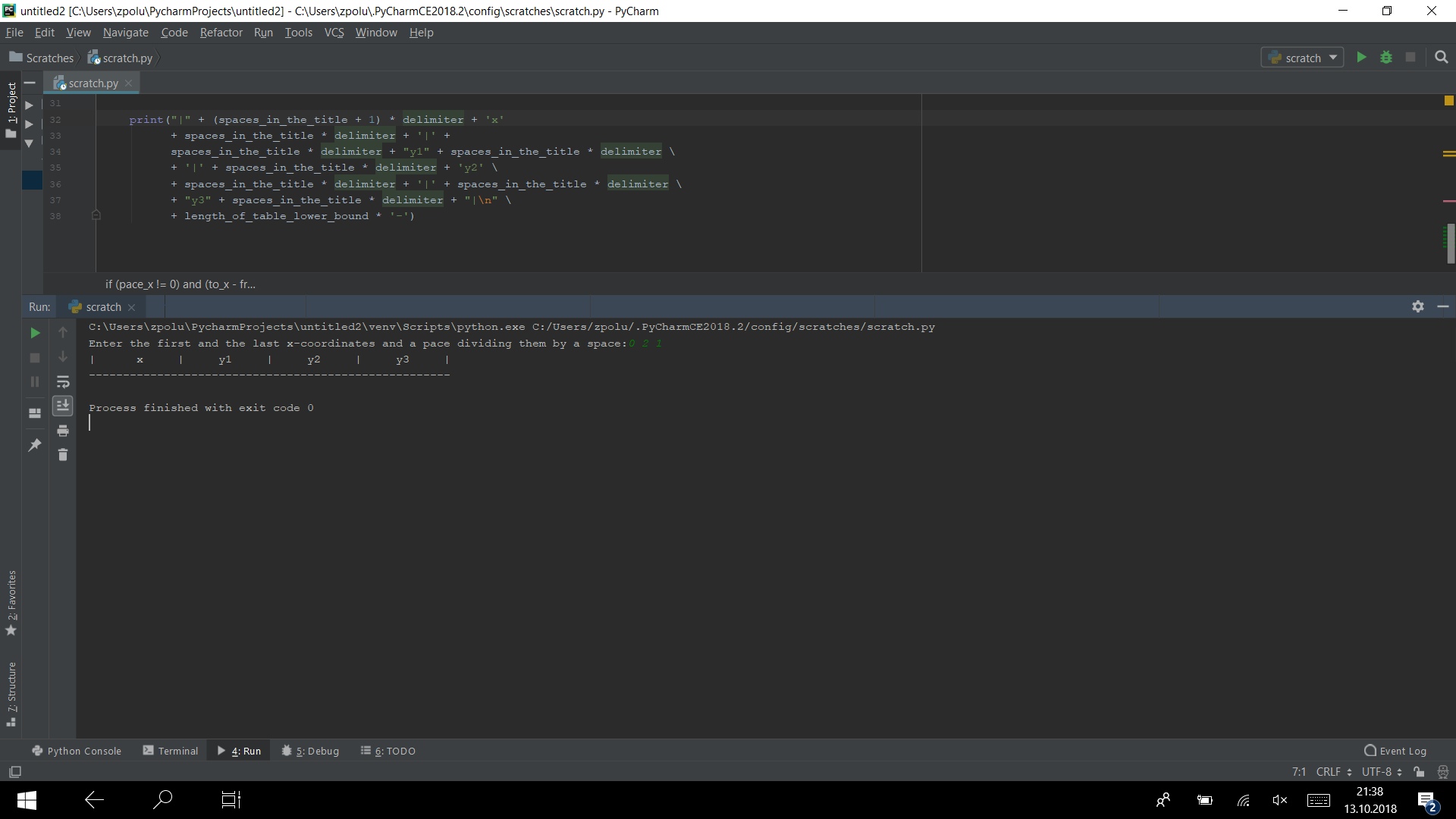
Теперь нам нужно печатать сами значения. Для этого понадобиться цикл. Так как введенные данные могут быть дробными, использовать range не получится, поэтому я буду использовать обычный цикл.
Так как у нас может быть как убывающая последовательность иксов, так и возрастающая, условия цикла должны быть поставлены так, что оба эти варианта учитываются. У нас есть ранее созданная переменная, которая хранит в себе ответ о характере последовательности в виде 0 или 1. Поэтому достаточно рассмотреть два случая и подобрать соответствующее условие к каждому
while(is_sequence_decreasing and x_copy >= to_x) or\
(not is_sequence_decreasing and x_copy <= to_x):
Так как для графика нам понадобятся минимум и максимум графика y1, который мы и будем рисовать, введем специальные переменные, которые будут отвечать за мин и макс
y1_cur_value = y1(x_copy)
min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \
(min_y1_value <= y1_cur_value) * min_y1_value
max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \
(max_y1_value >= y1_cur_value) * max_y1_value
negative_value_exists += y1_cur_value < 0
конструкция, по сути, повторяет конструкцию if: … else: …, только через булевы неравенства. y1_cur_value хранит текущее значение функции. Я создал переменную для того, чтобы не вызывать постоянно функцию, когда понадобится ее значение в точке.
Наличие отрицательных значений нам тоже потом понадобится для построения графика.
![]()
Теперь непосредственно печать значений. Я хочу, чтобы все было красиво и выравнено по центру в каждой из ячеек, поэтому придется вручную обрабатывать каждое значение, чтобы проверять длину числа и подбирать в зависимости от него кол-во пробелов для выравнивания значения.
Примечание
Буквально выровнять число по центру не получится. В переменной, отвечающей за точность есть параметр g. Он говорит о том, что для числа резервируется определенное количество позиций под цифры (в нашем случае, 10 по умолчанию). Если 10 цифр не набирается, то незаполненные цифрами позиции будут располагаться слева от заполненных позиций. Поэтому выравнять по центру мы можем только строку из 10 позиций.
aux_x = dials_precision % x_copy
aux = len(aux_x) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1
print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x — строка, которую уже привели к виду с заданной точностью. Теперь нам нужно проверить длину числа и подобрать необходимое количество пробелов. Так как больше одного пробела с каждой из сторон не понадобится, то boolевы переменные отлично подойдут в качестве хранителя количества этих самых пробелов. aux_2 отлавливает случай, когда длина числа равна 11.
Делаем также для значений трех функций
aux_y1 = dials_precision % y1_cur_value
aux = len(aux_y1) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='')
if (x_copy != 0):
aux_y2 = dials_precision % y2(x_copy)
aux = len(aux_y2) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='')
aux_y3 = dials_precision % y3(x_copy)
aux = len(aux_y3) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \
"|\n" + length_of_table_lower_bound * '-')
else:
print((spaces_in_the_title - 2) * delimiter + "не сущ" \
+ (spaces_in_the_title - 2) * delimiter + '|' \
+ (spaces_in_the_title - 2) * delimiter + "не сущ" \
+ (spaces_in_the_title - 2) * delimiter + "|\n" \
+ length_of_table_lower_bound * '-')
x_copy += pace_x
Как я уже говорил в самом начале, вторая и третья функции имеют точки разрыва — обе функции не существуют в точке x = 0. Поэтому эти случаи нам тоже нужно отловить.
Ну и не забываем увеличивать текущее значение икса, чтобы у нас не получилось бесконечного цикла.
Давайте соберем весь код в одну программу и запустим ее, например, на тесте -1.2 3.6 0.3

from math import sqrt
def y1(x):
return x**3 - 2*x**2 + 4*x - 8
def y2(x):
return 1 - 1/x**2
def y3(x):
return sqrt(abs(y1(x)*y2(x)))
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\
" x-coordinates and a pace dividing them by a"\
" space:").split())
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
dials_precision = "%10.6g" # точность числа
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
delimiter = ' '
is_sequence_decreasing = to_x - from_x < 0
min_y1_value, max_y1_value, x_copy = y1(from_x), y1(from_x), from_x
negative_value_exists = False
print("|" + (spaces_in_the_title + 1) * delimiter + 'x'
+ spaces_in_the_title * delimiter + '|' +
spaces_in_the_title * delimiter + "y1" + spaces_in_the_title * delimiter \
+ '|' + spaces_in_the_title * delimiter + 'y2' \
+ spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter \
+ "y3" + spaces_in_the_title * delimiter + "|\n" \
+ length_of_table_lower_bound * '-')
while (is_sequence_decreasing and x_copy >= to_x) or \
(not is_sequence_decreasing and x_copy <= to_x):
y1_cur_value = y1(x_copy)
min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \
(min_y1_value <= y1_cur_value) * min_y1_value
max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \
(max_y1_value >= y1_cur_value) * max_y1_value
negative_value_exists += y1_cur_value < 0
aux_x = dials_precision % x_copy
aux = len(aux_x) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1
print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_y1 = dials_precision % y1_cur_value
aux = len(aux_y1) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='')
if (x_copy != 0):
aux_y2 = dials_precision % y2(x_copy)
aux = len(aux_y2) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='')
aux_y3 = dials_precision % y3(x_copy)
aux = len(aux_y3) != int(dials_precision[1:3]) + 2
aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1
print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \
"|\n" + length_of_table_lower_bound * '-')
else:
print((spaces_in_the_title - 2) * delimiter + "не сущ" \
+ (spaces_in_the_title - 2) * delimiter + '|' \
+ (spaces_in_the_title - 2) * delimiter + "не сущ" \
+ (spaces_in_the_title - 2) * delimiter + "|\n" \
+ length_of_table_lower_bound * '-')
x_copy += pace_x
else:
print("Incorrect input")
Во второй части данного творения мы будем строить графики

To be continued…
