[Из песочницы] People meet recommender systems. Factorization03.02.2020 22:47

Машинное обучение довольно сильно проникло в нашу обыденную жизнь. Некоторые уже не удивляются, когда им рассказывают про нейронные сети в их смартфонах. Одной из больших областей в этой науке являются рекомендательные системы. Они есть везде: когда вы слушаете музыку, читаете книги, смотрите сериалы или видео. Развитие этой науки происходит в компаниях гигантах, таких как YouTube, Spotify и Netfilx. Конечно же, все научные достижения в этой области публикуются как на известных конференциях NeurIPS или ICML, так и на чуть менее известной RecSys, заточенной на эту тематику. И в этой статье мы поговорим, как развивалась эта наука, какие методы применяются в рекомендациях тогда и сейчас и какая математика за всем этим стоит.

На написание данной статьи меня вдохновила работа в лаборатории StatML в Skoltech, связанная с рекомендательными системами.

Зачем и для кого эта статья

Почему это может быть важно для каждого из нас? Посмотрите на представленный список:

Рекомендации видео: YouTube, Netlix, HBO, Amazon Prime, Disney+, Hulu, Окко
Рекомендации аудио: Spotify, Яндекс.Музыка, Яндекс.Радио, Apple Music
Рекомендации товаров: Amazon, Avito, LitRes, MyBook
Рекомендации в поиске: Google, Yandex, Bing, Yahoo, Mail
Остальные рекомендации: Booking, Twitter, Instagram, Яндекс.Дзен, Вконтакте, GitHub

Наверняка вы нашли один из сервисов, которым активно пользуетесь. Для меня важно, всегда заглядывать под капот машины и узнавать, как она устроена. Поэтому мне интересно знать, что происходит, когда мне рекомендуют новое видео в YouTube.

В интернете можно встретить хорошие статьи на эту тему (например от компании Яндекс), но порой люди говорят об одном и том же разными словами и возникает много путаницы. Кроме этого, существует очень мало мест, где можно найти весь зверинец моделей сразу. Поэтому я разобрался со всеми алгоритмами, и расскажу вам про них простыми словами (или не очень). Во-первых, фокус здесь будет направлен на математическую составляющую рекомендательных систем. И, во-вторых, это статья будет нацелена в большой степени на людей, которые имеют какое-то представление о машинном обучении. Но я надеюсь, что она будет полезна и новичкам. И конечно же, данный материал будет содержать формулы, поэтому я предполагаю, что у читателя есть некоторое представление о линейной алгебре, математическом анализе и теории оптимизации.

В реальности, конечно, все модели, о которых мы поговорим, являются лишь частью чего-то большего. Обычно используют огромные сборные модели со своей логикой, которая очень зависит от типов данных (кино, музыка, еда, одежда и т.д.). Например, есть интересная статья про такую систему.

Постановка задачи

Как и в любой другой задаче машинного обучения, задаче рекомендательной системы нужны обучающие данные. Для этого введем два множества: $U$ и $I$ — множества пользователей и товаров. А целевой переменной $r_{ui}$ будем считать результат взаимодействия пользователя $u$ и товара $i$ . К примеру, это может быть рейтинг фильма, который поставил пользователь, или же покупка товара, или добавление его в избранное. В итоге обучающей выборкой будет являться такое множество:

$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$

А нашей задачей будет являться восстановить зависимость и найти такую функцию $f$ :

$f(u, i) = \hat{r}_{ui}\approx r_{ui}$

Чтобы было ясно, $r_{ui}$ может быть целом числом от 1 до 5 (оценка от пользователя) или бинарной величиной: 1 или -1 (понравилось / не понравилось)

Виды рекомендательных систем

В литературе условно все методы делят на 3 типа:

Content-based (CB)
Collaborative filtering (CF)
Hybrid recommendations

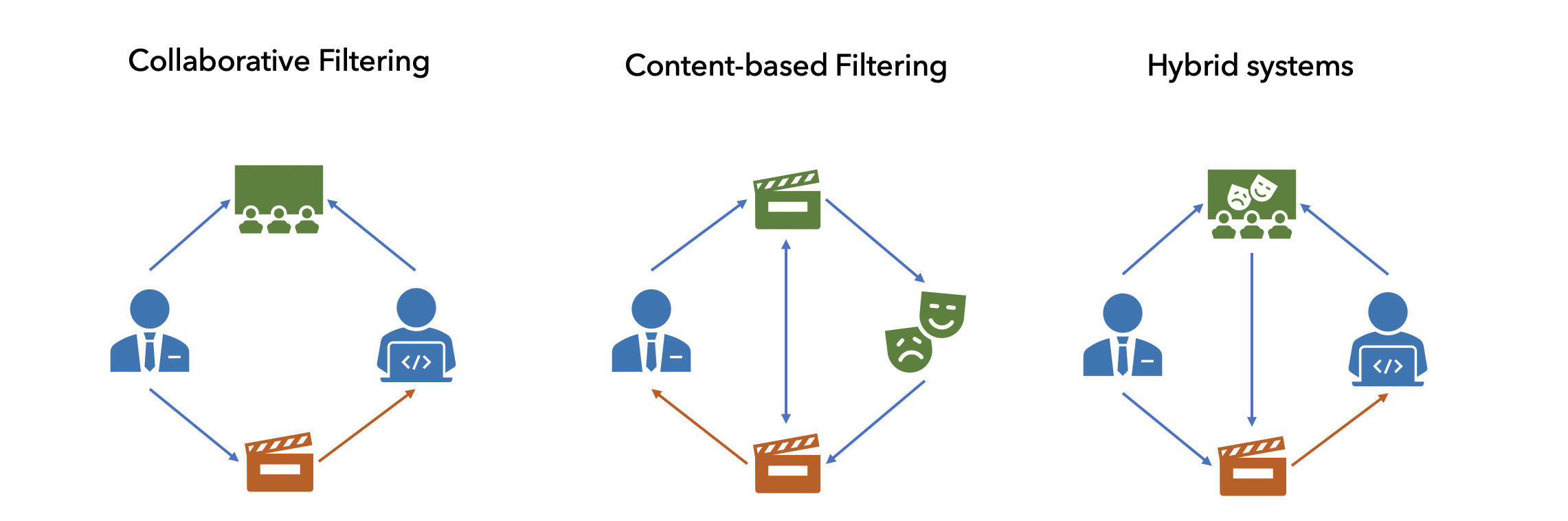
Контентные рекомендации берут всю информацию о товаре и пытаются найти похожий. Простой пример — мне понравилась комедия с Джимом Кери, поэтому мне порекомендовали другую комедию с этим актером. Признаки товаром могут быть разнообразны: для песни — сама его музыкальная дорожка, для товара в магазине — его фотография, параметры и характеристики. Чаще всего такие рекомендации тривиальны и их сможет повторить любой из нас. В таких моделях, мы так же можем использовать информацию о пользователе: пол, возраст и т.д.

Коллаборативная фильтрация не использует никакую информацию о товаре или пользователе, а строит свои рекомендации лишь на истории оценок. Ее главная задача найти какие-то скрытые связи там, где их нельзя найти обычному человеку.

А гибридные рекомендательные системы объединяют эти два подхода в себе. Практически все модели, которые используются в реальном мире, включают в себе помимо историй рекомендаций, еще и дополнительное знание о товарах и пользователях.

Поскольку материала оказалось очень много, я условно разделили все методы на Факторизационные, Графовые и Нейросетевые. В этой статье мы поговорим про первые из них. Отмечу, что в основном речь пойдет именно о коллаборативной фильтрации, но попутно я буду рассказывать про улучшение рассматриваемых моделей до гибридных. А в конце вас будет ждать приятный бонус.

Matrix Factorization

У нас был план, и мы ему следовали. Вот наш план: мы начнем с классических подходов. А далее добавив немного магии мы поговорим про их улучшения.

Классические подходы:
- Singular Value Decomposition (SVD)
- Singular Value Decomposition with implicit feedback (SVD++)
- Collaborative Filtering with Temporal Dynamics (TimeSVD++)
- Weighted Matrix Factorization (WMF or ALS)
- Sparse Linear Methods (SLIM)
- Factorization Machines (FM)
Вероятностные подходы:
- Probabilistic Matrix Factorization (PMF)
- Bayesian Probabilistic Matrix Factorization (BPMF)
- Bayesian Factorization Machines (BFM)
- Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

Начнем с самого простого и понятного метода — SVD. Мы можем записать все наши данные в матрицу $A$ размером $n \times m$ , где $n = |U|$ , а $m = |I|$ . Для известных пар из $\mathcal{D}$ мы запишем элемент матрицы $A_{ui} = r_{ui}$ , а все остальные приравняем к нулю. Используя SVD разложение, можно представить матрицу $A$ в виде произведения трех других: $U,~\Sigma,~V$ . Оставив $k$ самых больших по модулю сингулярных значений, можно сделать малораноговую аппроксимацию нашей матрицы $A$ .

$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$

Обозначим матрицу $Q$ и $P$ следующим образом. Тогда матрица $A$ представляется в виде такого произведения:

$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$

Или поэлементно это можно записать:

$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$

Получается, что $p_u$ и $q_i$ — это латентные представления пользователя $u$ и товара $i$ в каких-то пространствах размерности $k$ . На самом деле мы можем представить нашу модель в конечном виде и сразу искать латентные представления товаров и пользователей. Для этого просто поговорим немного об оптимизации. В данной задаче параметрами выступают латентные вектора:

$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$

И в этом случае они будут находиться при минимизации квадратичной ошибки c учетом регуляризации:

$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$

Стоит отметить, что большинство методов, о которых пойдет речь дальше, будут минимизировать функционал, записанный в левой части. Меняться будет лишь значение $\hat{r}_{ui}$ . А оптимизация будет происходить известными градиентным спуском (GD) или же чередованием наименьших квадратов (ALS). Что это и о чем это хорошо рассказано в этой Habr-статье или здесь, и я не вижу смысла тут повторяться. Хотелось бы лишь отметить тот факт, что градиентный спуск работает не только дольше, но и хуже.

Сразу поговорим про улучшение этого метода (иногда вместо обычного SVD, его называют SVD $_{bias}$ ). В реальности бывает так, что некоторые люди склонны завышать оценки товаров, а другие наоборот занижать. Так же и сами товары могут быть довольно популярны и менее популярны. Поэтому обычная модель SVD работает не так хорошо. Для решения этой проблемы нужно просто использовать обычное смещение (bias):

$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$

где $b_u$ — смещение для конкретного пользователя, $b_i$ — для товара, а $\mu$ — глобальное смещение. При этом количество параметров немного вырастит:

$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$

SVD++

В работе Factorization Meets the Neighborhood описывается новая модификация SVD модели. Но для начала поговорим про явный и неявный отклик от пользователя (explicit and implicit user feedback). Если по итогу взаимодействия между пользователем и товаром мы знаем оценку $r_{ui}$ , то это считается явным откликом. В противном случае мы знаем лишь об их взаимодействии и это неявный. Авторы статьи ассоциируют каждого пользователя с двумя группами товаров: $R(u)$ — множество товаров с явным откликом (рейтинги которых мы знаем) и $N(u)$ — множество товаров с неявным откликом (знаем лишь о наличии взаимодействия).

Метод SVD++ использует неявный отклик и в результате модель выглядит следующим образом:

$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$

В этом случае количество параметров увеличивается:

$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$

Поскольку неявный отклик иногда бывает недоступным, множество $N(u)$ можно заменить на $R(u)$ , т.к. всегда выполняется $R(u) \subset N(u)$ . А добавку данного метода можно расценивать как рекомендации товара к товару (item-item recommendation).

Asymmetric-SVD

Вместе с SVD++ авторы статьи предлагают другую модель. Идея этого метода так же является использование неявного отклика. В результате они получают:

$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$

где $b_{ui} = \mu + b_u + b_i$

TimeSVD++

Одним из широко известных гибридных моделей является TimeSVD++. В часто используемых данных (MovieLens, Netflix) помимо историй рейтингов фильмов от пользователей существует информация о времени, когда этот рейтинг был поставлен. Отсюда возникает законный вопрос, как это использовать. В статье Collaborative Filtering with Temporal Dynamics авторы предлагают в модель SVD++ добавить зависимость от времени:

$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$

Давайте разбираться, как именно влияет время на каждое слагаемое:
Item bias: Если разделить интервал времени, когда были проставлены рейтинги на отрезки (в работе предлагают 30 частей) и добавить свои собственные параметры $b_{i,\text{Bin}(t)}$ для каждого товара, которые выбираются в зависимости от того, в какой промежуток попала переменная $t$ :

$b_i(t) = b_i + b_{i, \text{Bin}(t)}$

User bias: Анализируя данные Neflix, заметили, что для каждого пользователя в среднем есть лишь 40 дней, в которые он расставлял рейтинги. Поэтому поступим как с товарами и добавим свои собственные параметры $b_{u, t}$ для каждого пользователя. Добавим линейную зависимость от времени — введем дополнительное слагаемое $\alpha_u$ с амортизационным коэффициентом:

$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$

.
Есть и другие варианты, как добавить зависимость от времени для пользователей: Более подробно расписано в статье
User embeddings: похожий трюк мы добавим для каждой компоненты нашего латентного представления $p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$ :

$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$

Weighted Matrix Factorization (WMF) & Alternating Least Squares (ALS)

Одной из главных проблем, которая есть в SVD, использование лишь явного отклика от пользователя. Это проблему частично решили в SVD++. Но есть и другой путь — Weighted Matrix Factorization (WMF). В это статье предложили почти не менять модель ( $\hat{r}_{ui} = p^T_u q_i$ ), а поменять процесс обучения. Присвоим для рейтингов $r_{ui}$ , которые мы не знаем (т.е. для пар $(u, i) \notin \mathcal{D}$ ) значение равное 0. А дальше для каждой пары $(u, i)$ введем параметр $c_{ui}$ , который будет отвечать за важность рейтинга $r_{ui}$ . Главный посыл в том, что нельзя полностью доверять явным признакам. Ведь пользователь мог купить какой-то товар как подарок для друга. Или просмотреть следующее видео в YouTube только потому, что отошел от компьютера. Плюс ко всему, мы хотим использовать не только рейтинги, которые знаем, но и не знаем. Именно поэтому мы изменим функционал, который будем минимизировать, таким образом, чтобы учесть все что можно:

$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$

Авторы статьи предлагают такой выбор параметров: $c_{ui} = 1 + \alpha r_{ui}$ . Такой выбор отвечает главной особенности: большое значение для тех $$r_{ui} > 0$» /> и маленькое для <img src=$ . Параметр $\alpha$ константный и в этой работе при $\alpha = 40$ модель дала хорошие результаты.

Так же стоит отметить тот факт, что в той же работе авторы используют (ALS) для обновления параметров. И в литературе можно встретить как метод WMF, так и ALS, но это одно и то же.

Fast Alternating Least Squares

Говоря про ALS метод, нельзя не рассказать про метод eALS описанный в этой статье. Метод не меняется, а меняется лишь способ обновления параметров. За счет более умной оптимизации с использованием кеша, параметры модели можно обновлять на лету. За счет этого этот метод хорошо зарекомендовал себя в онлайн рекомендациях.

Кроме этого, авторы предлагают новый вид для параметров $c_{ui}$ вместо предложенных в ALS методе:

$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$

с двумя новыми гиперпараметрами $c_0$ и $\beta$ , которые можно настроить на каждом наборе данных.

Sparse Linear Methods (SLIM)

В работе Sparse Linear Methods (SLIM) авторы статьи предлагают новый метод. Главной мотивацией послужило то, что SVD работает довольно долго. Поэтому они предложили простую модель основанную на идеи ближайших соседей в пространстве товаров. Модель SLIM выглядит следующим образом:

$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$

Тогда параметрами в этой задаче являются только веса $W \in \mathbb{R}^{m \times m}$ . Причем на эту матрицу весов мы накладываем некоторые ограничения: $W \geq 0$ и $\text{diag}(W) = 0$ . И эти веса подбираются в процессе минимизации следующего функционала:

$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$

Матрицу $W$ можно рассматривать как матрицу похожести или важности между всеми товарами.

Factorization Machines (FM)

Другой мощной моделью являются факторизационная машина, которая была предложена в работе Factorization Machines (FM). Допустим что целевая переменная зависит не только от самих признаков, но и еще от их попарного взаимодействия (полиномиальная регрессия 2-ого порядка). Тогда модель будет выглядеть следующим образом:

$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$

Оптимизация параметров происходит с помощью стохастического градиентного спуска (SGD) (более подробно можно прочитать в работе). Но до сих пор не до конца понятно, что такое $x$ и как оно связано с нашей парой $(u, i)$ . Более наглядно это будет видно на рисунке снизу. Первая часть вектора кодирует пользователя, вторая — товар. После можно добавить дополнительные признаки — историю просмотров пользователя (третья часть). Другие дополнительные признаки зависят лишь от данных и вашей креативности (жирный намек на гибридные методы).

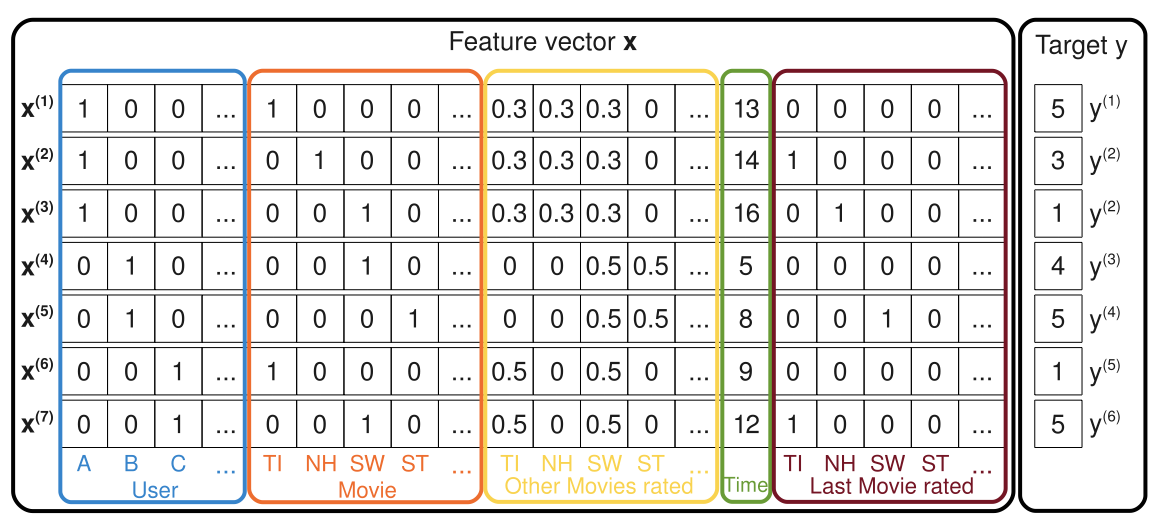
Так же авторы в этой статье показывают, что SVD, SVD++ — это лишь частные случаи FM. Например для SVD это легко видно, если обозначить:

$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$

где $\delta$ — символ Кронекера. Т.е. вектор $x$ состоит из нулей и двух единиц в индексах кодирующих $u$ и $i$ . Тогда в выражение для FM представится в виде:

$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$

Продолжим рассматривать картинку и увидим, что мы можем добавить абсолютно любые дополнительные признаки в переменную $x$ : время, последнюю рекомендацию. Например, у каждого фильма есть жанр, год выпуска, страна, режиссёр, сценарист, оператор и актерский состав. Все это можно добавить как признаки и использовать их в предсказании.

Probabilistic Matrix Factorization (PMF)

Дорогой читатель, хочу поздравить тебя, что ты дошел до этого момента, вот сейчас начнется самое сложное.

Другой мощной моделью считается вероятностная матричная факторизация (PMF), предложенная в этой статье. Главная идея, взять самый простой SVD: $p_u$ и $q_i$ — латентные вектора пользователей и товаров. Но в отличие от обычной модели, зададим вероятностную:

$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$

где $\mathcal{N}$ — нормальное распределение, a $g(x) = \frac{1}{1 + e^{-x}}$ — логистическая функция (сигмойда). Сделаем довольно сильное предположение, что наши пользователи и товары независимы, тогда латентные признаки будут распределены по Гаусу с нулевым средним и диагональной матрицей ковариации:

$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$

И если воспользоваться методом максимального правдоподобия (подробнее в статье) мы можем записать функционал, который будет минимизировать:

$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$

где $\lambda_p = \frac{\sigma_p}{\sigma}$ и $\lambda_q = \frac{\sigma_q}{\sigma}$ — регуляризационные множители. Стоит отметить, что если в обычном SVD они были гиперпараметрами, то здесь они могут подбираться автоматически.

Constrained PMF

В этой же работе последним улучшением обычного PMF является Constrained PMF. Мотивация почти та же сам, что при улучшении SVD до SVD++. Модель не меняется, за исключением того, что вместо $p_u$ мы используем:

$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$

где $R(u)$ — все то же множество товаров, рейтинги которых есть у пользователя $u$ .

Bayesian Probabilistic Matrix Factorization (BPMF)

И сразу же поговорим про улучшение PMF до BPMF. Существенным недостатком PMF модели является тот факт, что мы считаем, что пользователи и товары независимые. Мы можем это исправить поменяв вероятностное распределение:

$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$

Параметры $\Theta_p = \{ \mu_p, \Lambda_p \}$ и $\Theta_q = \{ \mu_q, \Lambda_q \}$ в свою очередь берутся из распределения Гаусса-Вишарта для которых мы зададим свои гиперпараметры $\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$ . Стоит сказать, что предсказание этой модели не совсем тривиальное и для более детального погружения стоит обратиться к первоисточнику.

Bayesian Factorization Machines (BFM)

Ну и конечно, один из лучших методов не может не получить приставку Bayesian, вот доказательства. Если вспомнить на секундочку обычную модель факторизационной машины, то нашими параметрами будет являться множество $\Theta = \{ w_0, w_i, v_i\} .$ Ключевая идея состоит в предположении, что каждый параметр принадлежит какому-то распределению. Для этого введем дополнительное множество гиперпараметров: $\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$ . После чего мы можем построить апостериорное распределение на наши параметры и с помощью некоторых хитрых техник сэмплировать из него.

Gaussian Process Factorization Machines (GPFM)

В статье про GPFM авторы решили к факторизационным машинам прикрутить гаусовские процессы. Ключевой идеей является введение специальной функции $f$ с параметрами $\theta$ . Причем для каждого пользователя параметры $\theta_u$ будут уникальными и для того, чтобы получить результат, нам необходимо будет лишь посчитать:

$\hat{r}_{ui} = f(q_i, \theta_u)$

У внимательного читателя возникнет вопрос, а причем тут гаусовские процессы. Дело в том, что сама функция $f$ как раз и берется из гаусовского процесса, с некоторым ядром. И примечательнее всего, что в этот момент мы можем добавить нелинейность при использовании, к примеру, экспоненциального ядра.

Так же в работе не уходят от возможности гибридного подхода и использую дополнительные латентные вектора для контентных признаков.

На десерт: Bayesian Personalized Ranking (BPR)

В конце хотелось бы рассказать про BPR модель, которая хорошо зарекомендовала себя в «продакшене». На самом деле, BPR — это не модель, а способ оптимизации, подробнее можно прочитать в работе Bayesian Personalized Ranking. Ну, а мы начнем разбирать в ней. Начнем с того, что здесь мы будем решать задачу ранжирования, когда для двух товаров $i$ и $j$ мы хотим выбрать наиболее релевантный для пользователя $u$ . Поэтому вместо пары $(u, i)$ и его рейтинга $r_{ui}$ будет рассматривать тройку $(u, i, j)$ и результат сравнения товара $i$ с товаром $j$ ((+) если $i$ нравится больше, чем $j$ и (-) наоборот). Множество таких троек назовем $\mathcal{D}_S$ . Так же введем вероятность для сравнения двух товаров. Причем результат сравнения зависит от пользователя (поэтому и есть приставка personalized в статье):

$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$

где $\sigma$ — сигмойда, a $\hat{r}_{uij}$ — задается моделью. Если воспользоваться методом максимального правдоподобия (MLE), мы можем записать функционал, который будем максимизировать:

$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$

А оптимизация происходит с помощью стохастического градиентного спуска (SGD):

$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$

До сих пор мы не говорили, какую модель мы берем. И на самом деле, мы можем воспользоваться любой классической моделью, о которых мы поговорили ранее. Выберем модель SVD:

$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$

И тогда для такой модели можно вычислить частные производные по параметрам:

$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$

У BPR подхода (как и у всех методов ранжирования) есть ряд преимуществ, по сравнению с обычными методами. Последние пытаются ввести меру на товар и пользователя, что не всегда получается сделать хорошо. Методы ранжирования лишены этой проблемы в некотором роде. При этом, попарная задача (pairwise approach) куда большая общая, чем предсказывание рейтинга (pointwise approach), т.е. такую задачу мы можем решать на разнообразных откликах. К примеру, мы показываем 5 товаров человеку, а он выбирает один. Тогда мы знаем, что выбранный товар ему нравится больше, чем любой из оставшихся. И последние преимущество — BPR не привязано к какой-то модели, а это лишь способ оптимизации. Поэтому, мы можем выбрать удобный нам метод или даже придумать свой.

Show must go on

В этот раз мы обсудили много Факторизационных методов в рекомендательных системах, но еще остались нетронутыми Графовые и Нейросетевые, в которых есть тоже очень много интересного.