[Из песочницы] Ограниченность преобразования Фурье или почему стоит доверять своему слуху28.12.2015 16:48

Последние несколько десятков лет задача распознавания аккордов музыкальной композиции ставилась довольно часто. Казалось бы, этот не столь оригинальный сервис был и остается довольно распространенным среди приложений, работающих со звуком (Ableton, Guitar Pro), однако универсального, срабатывающего всегда алгоритма не существует до сих пор. В этой статье я постараюсь раскрыть одну из множества причин неидеальной работы подобных сервисов на примере алгоритмов, использующих в своей основе преобразование Фурье.

Большинство аудиоформатов хранит информацию в виде зависимости амплитуды от времени (например, .wav) или в виде коэффициентов частотного преобразования (.mp3, .aac, .ogg), однако современные сложные алгоритмы цифровой обработки сигналов работают с частотной составляющей звуков. Приходится иметь дело с двойным переходом, из амплитудной области в частотную, затем обратно. На данный момент осуществление такого переход без потерь в качестве является достаточно распространенной проблемой с множеством неоднозначных решений.
Для разложения сигнала на частоты используется распространенное во многих областях преобразование Фурье. Поскольку в большинстве алгоритмах цифровой обработки сигналов приходится иметь дело с некоторой выборкой данных об амплитуде сигнала в конкретный момент времени, удобно использовать одну из многочисленных модификаций преобразования Фурье — дискретное преобразование Фурье. В своей классической интерпретации преобразование Фурье представляет собой сумму вида:

где N — количество компонент разложения,
xn, n = 0…N — 1 — значение отсчета сигнала в момент времени с номером n,
Xk, k = 0…N — 1 — выходные значения преобразования, представляющие собой искомые значения частот,
k — индекс частот.

Полученные в результате прямого преобразования значения Xk представляют собой набор комплексных значений — пар Re (Xk) + i*Im (Xk), характеризующих амплитуду и начальную фазу гармонического сигнала. Применив к полученным значениям обратное преобразование Фурье

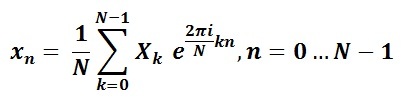
мы восстановим исходный сигнал с некоторой точностью. На практике же часто приходится работать с большими объемами данных. Для значительного ускорения вычисления используют быстрое преобразование Фурье, во многих современных библиотеках именуемое FFT (Fast Fourier Transform). FFT также работает с комплексными числами и отличается тем, что размер самого преобразования обязательно является степенью двойки, на практике это чаще всего мы видим числа 1024 или 2048. Варьируем размер преобразования и величину выборки, получаем приближенный к значениям реального сигнала набор отсчетов, воздействуем на него обратным преобразованием Фурье, и на выходе перед нами исходные частоты, а значит, получение звучавшей последовательности аккордов не должно представлять особой сложности.

Однако. Преобразование Фурье любого вида является сложным универсальным инструментом, сильно зависящим от поставляемых ему данных. Непрерывное преобразование Фурье является развитием идеи рядов Фурье, более обобщенной, результирующим значением частот которого являются комплексные числа. Мы смотрим на классическое прямое преобразование

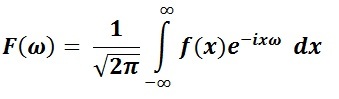
и видим в его реализации интеграл на бесконечном промежутке, на дискретное преобразование — это бесконечная сумма ряда. И о справедливости равенства правой и левой частей мы можем говорить только в том случае, когда исходная функция является функцией бесконечной длины, только тогда, когда перед нами представлен бесконечный сигнал. Легко согласиться, что на практике такие сигналы встретишь не часто.

Создадим искусственный сигнал, соответствующий ноте Ля, взятой в двух разных октавах (частоты равны соответственно 440 Гц и 3440 Гц), пропустим его через прямое преобразование Фурье, а затем через обратное:

dt = 0.001;
T = 1;
t=0:dt:T;
w = 440;
q = 2^(1/12);
//исходный сигнал
x = cos(2*%pi*w*t*q^1) + cos(2*%pi*w*t*q^4);
scf(0);
plot2d(x, rect=[0,0,1200,2]);

// сигнал после преобразования Фурье
y = fft(x);
scf(1);
plot(y);

// обратное преобразование Фурье
z = fft(y,-1);
z1 = z/(T/dt);

scf(2);
plot2d(x, style=[color("red")], rect=[0,0,1200,2]);
plot2d(z1,style=[color("green")], rect=[0,0,1200,2]);

Запускаем код Scilab и видим, что исходный сигнал (x) и сигнал, полученный обратным преобразованием (z1), мягко говоря, разные:

Рис. 1 График функции x исходного сигнала (красный цвет) и восстановленного сигнала z1 (желтый цвет)

Как обходят подобные ограничения с бесконечностью? Поскольку перевод сигнала в частотное представление при помощи FFT производится только блоками, у каждого такого блока мы можем увеличить частоту дискретизации, тем самым увеличив размер FFT блока и, соответственно, количество коэффициентов преобразования. Это даст нам более точный частотный результат на единицу времени. Достаточно разумный подход.

Но как бы мы не приближали длину промежутка к бесконечности, неточности все равно будут иметь место. FFT не знает ничего об исходных гармониках функции. В нашем случае, имелась частота в 440 Гц, а FFT превратил ее в набор гармоник с искаженными частотами, хоть и близкими по значению к исходной. Поэтому полученные значения сигнала являются лишь близкими к первоначальному. Чтобы ликвидировать это искажение, применяются так называемые оконные функции. Перед разложением блок FFT перемножается на оконную функцию W (ω — t), где t — момент времени, соответствующий текущему отсчету. Основное влияние оконной функции заключается в уменьшении коэффициентов перед мнимыми частотами в разложении, тем самым уменьшая их вклад в конечную частотную картину.

Но как мы поймем, что мы отсекли действительно «незначительные» частотные пики? Конечно, можно пытаться экспериментировать с разбиениями и их длиной, длиной промежутков с нулевыми коэффициентами вне оконной функции, однако это лишь частично сгладит итоговую картину. Взять хотя бы случай, когда искомые ноты имеют достаточно низкие частоты, здесь мы можем получить мнимые значения частот, значительно превышающие исходный материал!

Здесь уже явно стоит попробовать эксперименты с оконными функциями разного вида. Например, классическая прямоугольная оконная функция

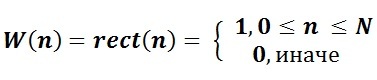
сохранит все исходные значения частот. Но если мы возьмем, скажем, треугольное окно

станет очевидно, что краевые выбивающиеся значения попросту отсекутся, с высокой долей вероятности останется наиболее чистая информация.

Однако. Снова сгенерируем простой ограниченный сигнал и вычислим его спектр:

scf(0);
t=0:0.0001:3*%pi;
x = sin(t);
plot2d(t,x);

y = simp(fft(x));
scf(1);
plot2d(y, rect = [-100, -10000, 40000, 10000]);
disp(y(1000));

Исходный сигнал х:

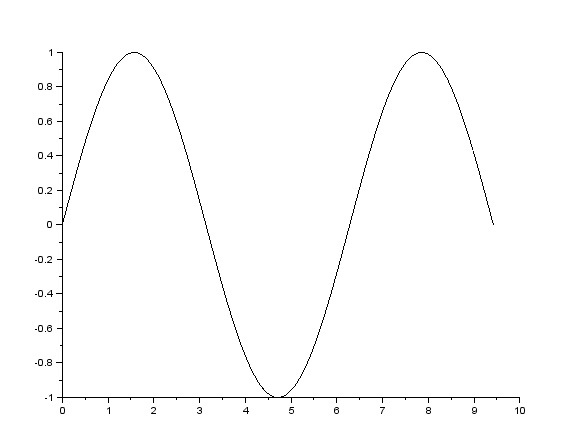
Рис. 2 Исходный сигнал х

Рис. 3 Спектр сигнала y

Что же мы видим? Спектр перестал быть ограниченным, по обоим его сторонам образовались лишние значения, более того, их бесконечное число! Случилось что? В тех двух точках, где произошло соприкосновение с краями оконной функции, функция перестала быть гладкой. На вход Фурье-преобразование ожидает увидеть сигнал, представляющий собой сумму простых синусоид, где точки разрыва можно получить только с помощью бесконечной суммы этих синусоид.

Вот мы уже напрямую столкнулись с самым настоящим принципом неопределенности для области обработки сигналов. Принцип здесь носит название Теоремы Бенедика: функция не может быть одновременно ограниченной в диапазоне времени и в диапазоне частоты. В более строгой формулировке теорема звучит так: функция в пространстве и ее отображение Фурье не могут одновременно иметь один и тот же носитель функции на покрытиях с ограниченной мерой Лебега. И если с сигналами бесконечной длины дело приходится иметь редко, и эта область для практики имеет меньшее значение, то что же со случаем, когда сигнал имеет конечную длину?

И здесь мы не обойдемся без самой известной теоремы в теории обработки звуковых сигналов — теоремы Котельникова-Найкваиста-Шеннона, которая в одной из свои интерпретаций звучит следующим образом: любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчетам тогда, когда значения его отсчетов f > 2Fmax, где Fmax — максимальная частота, которой ограничен спектр исходного сигнала. Исходя из этой теоремы и теоремы Бенедика мы делаем вывод, что в данный момент реальных сигналов, которые можно с бесконечно большой точностью представить в дискретном и ограниченном виде, нет. Мы всегда либо будем иметь дело с сигналом бесконечно большой длины, либо будем получать в ограниченном сигнале неточности разной степени, которые в итоге могут значительно испортить картину исходной аудиозаписи.

Конечно, разработчики подобных сервисов, работающих со звуками, эту проблему в какой-то мере решают. Используют ступенчатую интерполяцию, разные виды линейной интерполяции, фильтры нижних частот для борьбы с отсчетами, превышающими половину частоты дискретизации. Их самыми распространенными недостатками являются данные, которые лишь грубо приближены к исходным значениям частот, а также наличие высокочастотного мусора. Однако и аудиозаписи, с которыми приходится иметь дело, тоже далеко не идеальны. Высокий уровень шума, скорость записи, качество звукозаписи. Здесь уже нужно уметь адаптироваться под каждый сигнал, вычислять скорость игры, длительность аккордов, гасить белый (в лучшем случае) шум, но это уже совсем другая история.