[Из песочницы] Однослойный перцептрон для начинающих
В последнее время всё чаще стали появляться статьи о машинном обучении и о нейронных сетях. «Нейронная сеть написала классическую музыку», «Нейронная сеть распознала стиль по интерьеру», нейронные сети научились очень многому, и на волне возрастющего интереса к этой теме я решил сам написать хотя бы небольшую нейронную сеть, не имея специальных знаний и навыков.
К своему большому удивлению, я не нашел простейших и прозрачных примеров а-ля «Hello world». Да, есть coursera и потрясающий Andrew Ng, есть статьи про нейронные сети на хабре (советую остановиться тут и прочитать, если не знаете самых основ), но нет простейшего примера с кодом. Я решил создать перцептрон для распознования «AND» или «OR» на своем любимом языке C++. Если вам интересно, добро пожаловать под кат.
Итак, что же нам потребуется для создания такой сети:
1) Основные знания C++.
2) Библиотека линейной алгебры Armadillo.
В ArchLinux она ставится просто:
yaourt -S armadillo
Создадим два файла: CMakeLists.txt и Main.cpp.
CMakeLists.txt отвечает за конфигурацию проекта и содержит следующий код:
project(Perc)
cmake_minimum_required(VERSION 3.2)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")
set(CMAKE_BUILD_TYPE Debug)
set(EXECUTABLE_NAME "Perc")
file(GLOB SRC
"*.h"
"*.cpp"
)
#Subdirectories
option(USE_CLANG "build application with clang" ON)
find_package(Armadillo REQUIRED)
include_directories(${ARMADILLO_INCLUDE_DIRS})
set(CMAKE_RUNTIME_OUTPUT_DIRECTORY "${CMAKE_CURRENT_SOURCE_DIR}/bin")
add_executable(${EXECUTABLE_NAME} ${SRC} )
TARGET_LINK_LIBRARIES( ${EXECUTABLE_NAME} ${ARMADILLO_LIBRARIES} )
Main.cpp:
#include
#include
using namespace std;
using namespace arma;
int main(int argc, char** argv)
{
mat A = randu(4,5);
mat B = randu(4,5);
cout << A*B.t() << endl;
return 0;
}
Это тестовый пример для того, чтобы проверить, все ли правильно настроено.
cmake
make
./bin/NeuroBot
Если все работает, то продолжаем!
Как же нейронная сеть работает и понимает, что есть AND, а что есть OR? Так она выглядит:
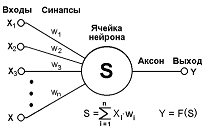
Строго говоря, это лишь нейрон, но в то же время это и основной концепт сети. Обо всем по порядку:
x1 и x2 и x…- наши входные данные. Возьмем логическое «AND»
Наши входные данные — A и B, то есть матрица 4×2, так как с матрицами удобнее работать.
w1 и w2 — «веса», это то, что нейронная сеть и будет обучать. Обычно весов на один больше чем входов, в нашем случае их 3 (+ биас).
Опять матрица: 3×1.
Y — выход, это наш результат, он будет полностью совпадать с Q. Матрица 4×1. Матрицы очень удобно использовать с векторизацией.
Ячейка нейрона — это нейрон, который будет учить w1 и w2. В нашем случае это будет логистическая регрессия. Для обучения w1 и w2 мы будем использовать алгоритм градиентного спуска.
Почему логистическая регрессия и градиентный спуск? Логистическая регрессия используется потому, что это логическая задача 0 / 1. Логистическа регрессия (сигмоида) строит гладкую монотонную нелинейную функцую, имеющую форму буквы «S»:
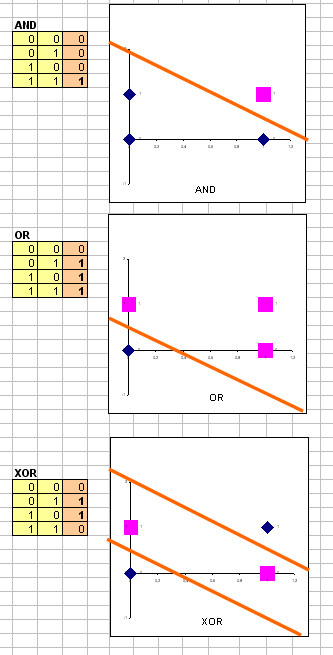
Широко известна также линейная регрессия, но она в основном используется для классификации больших объемов данных. Градиентный спуск — это самый распрастранненый способ обучения, он находит локальный экстремум с помощью движения вдоль градиента (просто спускается).
На этом теоретическая часть заканчивается, перейдем к практике!
Итак, алгоритм следующий:
1) Задаем на вход данные
const int n = 2; //Количество нейронов
const int epoches = 100; //Количество эпох, сколько раз мы "подгоняем" w1 и w2
double lr = 1.0; //Коэффициент обучения
mat samples({
0.0, 0.0, 1.0,
1.0, 0.0, 1.0,
0.0, 1.0, 1.0,
1.0, 1.0, 1.0
});
samples.set_size(4, 3);
//Ответы
mat targets{0.0, 0.0, 0.0, 1.0};
targets.set_size(4, 1);
mat w; w.set_size(3,1);
//Случайные весы от -1 до 1
w.transform([](double val)
{
double f = (double)rand() / RAND_MAX;
val= 1.0 + f * (-1.0 - 1.0);
return val;
});
2) Пока количество эпох не подошло к концу (альтернативный способ: сравнивать заготовленные ответы с полученными и остановиться при первом совпадении), умножаем веса на входные данные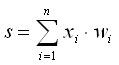 
, применяем логистическую регрессию (сигмоида — sig), 
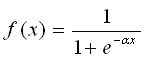подправляем веса с помощью градиентного спуска.
for(int i = 0; i < epoches; i++)
{
mat z = samples * w; //Summator
auto outputs = sig(z);
//Gradient Descend
w -= (lr*((outputs - targets) % sig_der(outputs)).t() * (samples) / samples.size ()).t();
std::cout << outputs << std::endl << std::endl;
}
3) В конце запускаем активационную функцию (Аксон), округляем матрицу и выводим результат.
//Activate function
mat a = samples * w;
mat result = round(sig(a));
std::cout << result;
Перцептрон готов. Измените Y на «OR» и убедитесь, что все правильно работает.
Если вам понравилась статья, то я обязательно распишу, как работает многослойный перцептрон на примере XOR, объясню регуляризацию, и мы дополним имеющийся код.
Ссылка на Main.cpp gist.github.com/Warezovvv/0c1e25723be1e600d8f2.
