[Из песочницы] Моделируем вселенную: небесная механика наглядно

Давайте представим, что нам нужно запустить футбольный мяч на орбиту Земли. Никакие ракеты не нужны! Хватит горы, высотой 100 километров и недюжинной силы. Но насколько сильно нужно пнуть мяч, чтобы он никогда больше не вернулся на Землю? Как отправить мяч в путешествие к звёздам, имея только грубую силу и знание небесной механики?
Сегодня в программе:
- Бесконечные возможности одной формулы
- Как взять энергию у Юпитера
- Откуда у планет берутся кольца
- Как математика помогла открыть Нептун
Благо, мы живём в век компьютерных технологий. Нам не нужно забираться на высокую гору и пинать мяч со всей силы, всё можно смоделировать! Давайте приступим.
Одна формула
Та самая, известная с уроков физики и астрономии:
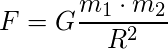
Показывает, насколько сильно будут взаимодействовать тела, в зависимости от их масс, расстояния между ними и гравитационной постоянной G.
Я написал программу, в которой можно расставлять шарики, взаимодействующие друг с другом силами гравитации, при этом у каждого шарика есть своя масса, скорость и координаты. Для наглядности шарики оставляют за собой след.
Давайте поставим большой и массивный голубой шар (Землю) и маленький красный мячик недалеко от него. Запускаем симуляцию:

Он упал!
Для выхода на орбиту нужна скорость, чтобы шарик падал и все время промахивался мимо Земли. Но КАКАЯ скорость? И снова школьные знания приходят на помощь:
Минимальная скорость, необходимая для выхода на орбиту Земли называется первой комической скоростью.
Для Земли она равна 7.91 км/с. А для симуляции её можно легко вычислить:
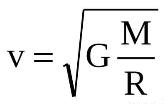
Разгоняем мячик и смотрим результат:

Полёт нормальный!
Шарик описывает окружность с Землёй в центре. Что будет, если придать ему чуть больше скорости? Сейчас проверим:

Теперь форма орбиты эллиптическая, можно выделить 2 очень важные точки — апогей и перигей.
Апогей — это точка, в которой мячик максимально удалён от Земли.
Перигей — наоборот, самая близкая к Земле точка.
При увеличении начальной скорости перигей не меняется, а вот апогей становится всё дальше, и в конце концов имеет бесконечное расстояние до Земли. Тут мы вплотную приблизились к понятию второй космической скорости. Это скорость, которую надо придать шарику, чтобы он преодолел гравитацию Земли и улетел бороздить просторы вселенной. Для земли она равна 11.2 км/с.
Интересный фокус: если мы умножим первую космическую скорость на √2, то получим вторую космическую.
Умножили. Запустили. Получили:

Он улетел безвозвратно! Кстати, теперь он имеет параболическую орбиту. А если запустить шарик ещё сильнее, получим гиперболу. Интересно получается, везде нас преследует математика.
При этом формула остаётся всё той же. Окружность превращается в эллипс, эллипс в параболу, а парабола в гиперболу из-за вытягивания орбиты (увеличения эксцентриситета).
Как взять энергию у Юпитера?
Давайте расширим нашу модель, добавим Солнце, заставим Землю крутиться вокруг него.

Представим, что мячу нужно придать такую скорость, чтобы он улетел за пределы Солнечной системы — третью космическую скорость. В реальном мире она равна 16.7 км/с. К сожалению, эта скорость слишком большая, боюсь, нам не хватит сил…
Постойте! А что, если забрать немного скорости у какого-нибудь массивного тела, например, Юпитера. Мы можем подлететь к чему-то очень массивному и совершить гравитационный манёвр. При пролёте мимо Юпитера силы гравитации взаимно притягивают мячик и газовый гигант, но масса мячика настолько мала, что почти никак не влияет на движение Юпитера, а сам Юпитер разгоняет пролетающее мимо тело до высоких скоростей.
Меньше слов — больше дела:

Момент гравитационного манёвра — шарик подлетел к Юпитеру.

Ура! Мы получили скорость, достаточную для выхода из Солнечной системы, при этом ничего не потратили. Правда, Юпитер стал двигаться чуть медленнее, но мы этого точно не заметим.
Все космические аппараты, запущенные человеком за пределы солнечной системы («Вояджеры» 1 и 2, «Пионеры» 10 и 11, «Новые горизонты») использовали именно такой способ для ускорения.
Увеличиваем масштаб!
Я добавил трение частиц, чтобы, сталкиваясь, они передавали часть энергии друг другу. Также я ввёл силу нормальной реакции, теперь частицы уважают своё личное пространство, отталкивая от себя других.
Поставим случайную генерацию шариков и зададим им случайное направление и скорость. Пусть их будет, допустим, 100 штук.
Полный хаос, каждая частица движется куда хочет, но всё же силы гравитации берут своё, и начинают образовываться скопления шариков:
И через некоторое время получается большое тело, состоящее из 99 шариков и один-единственный шарик, обращающийся вокруг него:

При другом запуске получилось следующее:

Два массивных тела, обращающихся вокруг общего центра масс. Если представить, что эти два объекта — звёзды, то мы получили двойную звезду. Интересно, что примерно половина звёзд в нашей галактике — двойные. Если бы у нашего Солнца была звезда — компаньон, то в небе мы могли бы наблюдать такую картину:

Откуда у планет берутся кольца?
Основная причина появления колец — это разрушение спутников, подлетевших слишком близко к планете, а точнее, пересёкших предел Роша. В таком случае приливные силы, вызываемые гравитацией планеты, становятся больше сил, удерживающих спутник целым, и он разрывается на много частей, оставляя после себя кольцо, которое опоясывает планету. Давайте смоделируем эту ситуацию:

Спутник чуть дальше предела Роша, он вращается вокруг планеты по стабильной круговой орбите. Но что будет, если сгенерировать его чуть-чуть ближе к планете?
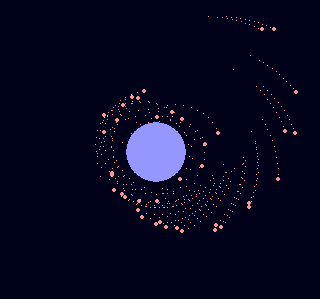
Спутник разлетелся на множество маленьких частей, которые образовали кольца вокруг планеты. Так же и в реальном мире. Тритон (спутник Нептуна) постепенно приближается к планете, и через 2 миллиарда лет будет разорван, а у Нептуна появятся кольца больше, чем у Сатурна.
Как открыли Нептун и при чём здесь математика?
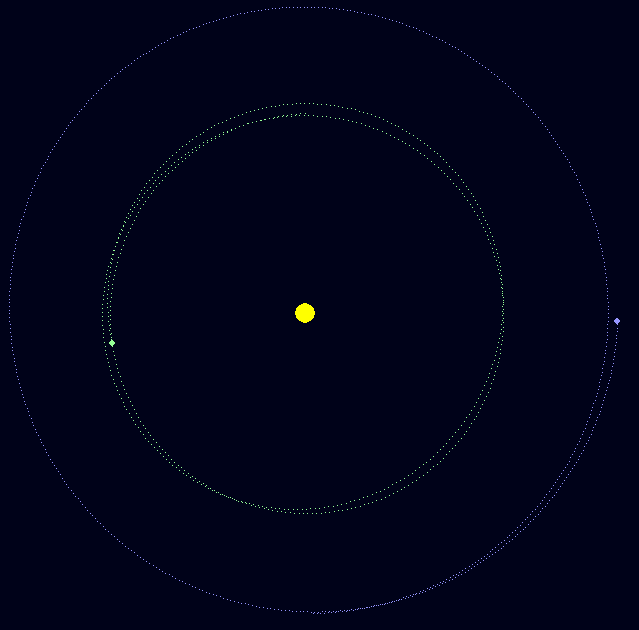
Раз уж зашла речь о Нептуне, давайте поговорим о его открытии. «Планета, открытая на кончике пера» имеет массу, а значит, действует на объекты вокруг. Астрономы 19 века заметили изменения в орбите Урана, его орбита отличалась от расчётной, видимо, что-то влияло на него. Орбита Урана имела возмущения:
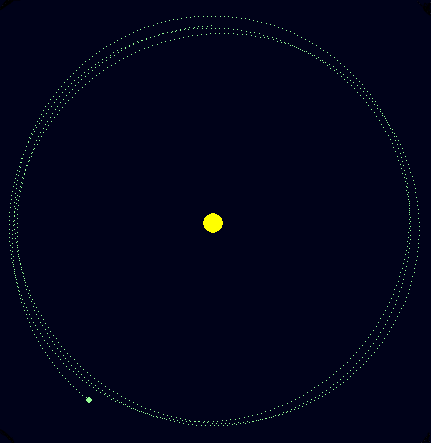
Это утрированная модель показывает, как неизвестное тело за Ураном влияло на его орбиту. Астрономам оставалось только вычислить положение тайной планеты и посмотреть в телескоп. Действительно, планета Нептун оказалась именно там, где её и предсказывали!
Заключение
Конечно, эта симуляция не обобщает все законы и явления, происходящие в космосе, например, здесь не учитывается теория относительности Эйнштейна, так как скорость частиц далека от скорости света. Но есть ещё много интересных вещей, которые можно реализовать в этой симуляции. Попробуйте сами! Понадобится только Python3 и библиотека Pygame.
#Траектория частицы
Track = True
#длина траектории
Track_time = 5
#Гравитационная постоянная
G = 5
#Сила магнитного взаимодействия(одинаковые цвета -
#притягиваются, разные - отталкиваются)
MagnConst = 0
#Количество частиц
count = 100
#Начальная скорость частиц
kv = 6
#Случайная генерация частиц
RANDOM = True
#Радиус случайных частиц
r = 3
#Ширина и высота окна
WIN_WIDTH, WIN_HEIGHT = 900, 650
'''всё, что дальше, лучше не менять'''
#Закон для гравитационного взаимодействия
zg = 2
#Закон для магнитного взаимодействия
zm = 2
#Коэф. трения, чем он больше - тем меньше трение
k = 40
#Отталкивание частиц
antiG = 0.1
max_speed = 3
ResDist = 1
#Притяжение вниз
EarthG = 0
#Отражение частиц от стенок
Mirror = True
import pygame
from math import hypot, ceil, sqrt
from random import randint, random
def custom_pos():
'''Здесь вы можете написать своё расположение планет'''
'''не забудьте установить RANDOM = FALSE'''
B.append(Ball(200, 300, YELLOW, r = 10, mass = 200, vx = 0.151)) #x, y, col, r, vx, vy, mass
B.append(Ball(200, 50, GREEN, r = 6, mass = 10, vx = -(200 * G / 250)**0.5))
class Ball:
def __init__(self, x, y, col, r = 4, vx = 0, vy = 0, mass = 4):
self.x = x
self.y = y
self.r = r
self.col = col
self.vx = vx
self.vy = vy
self.mass = mass
def move(self, Walls, WIN_WIDTH, WIN_HEIGHT, ofs_x, ofs_y):
if Walls:
x = self.x - ofs_x
y = self.y - ofs_y
if x <= 0 and self.vx < 0:
if Mirror:
self.vx = -self.vx
else:
self.x += WIN_WIDTH
self.vx, self.vy = self.v_norm(self.vx, self.vy)
if x >= WIN_WIDTH and self.vx > 0:
if Mirror:
self.vx = -self.vx
else:
self.x -= WIN_WIDTH
self.vx, self.vy = self.v_norm(self.vx, self.vy)
if y <= 0 and self.vy < 0:
if Mirror:
self.vy = -self.vy
else:
self.y += WIN_HEIGHT
self.vx, self.vy = self.v_norm(self.vx, self.vy)
if y >= WIN_HEIGHT and self.vy > 0:
if Mirror:
self.vy = -self.vy
else:
self.y -= WIN_HEIGHT
self.vx, self.vy = self.v_norm(self.vx, self.vy)
self.x += self.vx
self.y += self.vy
def force(self, ind, selfind):
ox = B[ind].x
oy = B[ind].y
m = B[ind].mass
if m < 0.01 and self.mass < 0.01:
return 0
r = B[ind].r
vx = B[ind].vx
vy = B[ind].vy
dist = hypot(self.x - ox, self.y - oy)
min_dist = (self.r + B[ind].r) * ResDist
f = 0
m_relative = self.mass / B[ind].mass
if dist <= min_dist:
newVx = (vx * m + self.vx * self.mass) / (m + self.mass)
newVy = (vy * m + self.vy * self.mass) / (m + self.mass)
self.vx = (newVx + k * self.vx) / (k + 1)
B[ind].vx = (newVx + k * B[ind].vx) / (k + 1)
self.vy = (newVy + k * self.vy) / (k + 1)
B[ind].vy = (newVy + k * B[ind].vy) / (k + 1)
f -= antiG * min(abs(min_dist - dist), min(m, self.mass) * 3)
else:
f += min(self.mass * B[ind].mass * G / (dist ** zg), G / 10)
mf = MagnConst * self.mass / (dist ** zm)
if B[ind].col == B[selfind].col:
mf = - mf
f += mf
fx = f * ((ox - self.x) / dist)
fy = f * ((oy - self.y) / dist)
ax = fx / self.mass
ay = fy / self.mass
self.vx += ax
self.vy += ay + EarthG
B[ind].vx -= ax * m_relative
B[ind].vy -= ay * m_relative - EarthG
@staticmethod
def v_norm(vx, vy):
v = hypot(vx, vy)
if v > max_speed:
vx = max_speed * (vx / v)
vy = max_speed * (vy / v)
return vx, vy
class Point:
def __init__(self, x, y, col, r = 0, max_age = Track_time):
self.age = 0
self.x = x
self.y = y
self.col = col
self.r = r
self.max_age = max_age
def vis(self, ofs_x, ofs_y):
pygame.draw.circle(sc, self.col, (round(self.x - ofs_x),
round(self.y - ofs_y)), self.r, 0)
self.age += 1
if self.age > self.max_age:
T.remove(self)
def rand(count, WIN_WIDTH, WIN_HEIGHT):
global kv
B = []
for i in range(count):
m = r ** 2
x = randint(0, WIN_WIDTH) + random()
y = randint(0, WIN_HEIGHT) + random()
vx = kv * randint(-100, 100) / 100
vy = kv * randint(-100, 100) / 100
col = Colors[randint(0, len(Colors) - 1)]
B.append(Ball(x, y, col, r = r, vx = vx, vy = vy, mass = m))
return B
def createBall(col, x, y, r = r, m = r):
m = r
B.append(Ball(x, y, col))
def get_offset(B):
sum_x, sum_y = 0, 0
m = 0
for i in range(len(B)):
sum_x += B[i].x * B[i].mass
sum_y += B[i].y * B[i].mass
m += B[i].mass
if len(B) == 0:
return 0, 0
return sum_x / m, sum_y / m
def visBalls(B):
for i in range(len(B)):
pygame.draw.circle(sc, B[i].col, (round(B[i].x - ofs_x),
round(B[i].y - ofs_y)), B[i].r, 0)
T.append(Point(B[i].x, B[i].y, B[i].col))
FPS = 60
darkblue = (0, 2, 25)
ORANGE = (255, 200, 150)
RED = (255, 150, 150)
GREEN = (150, 255, 150)
BLUE = (150, 150, 255)
YELLOW = (255, 255, 0)
Colors = [RED, BLUE]#, GREEN]#, ORANGE]
pygame.init()
clock = pygame.time.Clock()
sc = pygame.display.set_mode((WIN_WIDTH, WIN_HEIGHT))
sc.fill(darkblue)
maxF = 0.3
minv = 0.01
Walls = True
Collisions = True
Same = True
Check = False
tt = []
B = []
if RANDOM:
B = rand(count, WIN_WIDTH, WIN_HEIGHT)
else:
custom_pos()
Pause = False
delay = 0
if Track:
T = []
for z in range(100000):
sc = pygame.display.set_mode((WIN_WIDTH, WIN_HEIGHT))
sc.fill(darkblue)
ofs_x, ofs_y = get_offset(B)
ofs_x -= WIN_WIDTH // 2
ofs_y -= WIN_HEIGHT // 2
for i in pygame.event.get():
if i.type == pygame.QUIT:
pygame.quit()
quit()
if i.type == pygame.KEYDOWN:
if i.key == pygame.K_SPACE:
Pause = not Pause
elif i.key == pygame.K_w:
WIN_HEIGHT += 10
WIN_WIDTH += 10
elif i.key == pygame.K_s:
WIN_HEIGHT -= 10
WIN_WIDTH -= 10
pressed = pygame.mouse.get_pressed()
pos = pygame.mouse.get_pos()
x = pos[0]
y = pos[1]
if pressed[0] and delay < 0:
delay = 20
createBall(RED, x + ofs_x, y + ofs_y)
if pressed[2] and delay < 0:
delay = 20
createBall(BLUE, x + ofs_x, y + ofs_y )
delay -= 1
if not Pause:
for i in range(len(B)):
for j in range(i + 1, len(B)):
B[i].force(j, i)
for i in range(len(B)):
B[i].move(Walls, WIN_WIDTH, WIN_HEIGHT, ofs_x, ofs_y)
for i in range(len(T)):
try:
T[i].vis(ofs_x, ofs_y)
except IndexError:
pass
visBalls(B)
pygame.display.update()
clock.tick(FPS)
Надеюсь, эта статья оказалась познавательной для вас. Спасибо за внимание!
