[Из песочницы] Моделируем алгоритм MUSIC для задач определения направления прихода электромагнитной волны03.04.2019 22:50

aaspcats

Предисловие

Начну своё вступление издалека. Давным-давно, в далеких 2016–2017 годах вашему покорному слуге удалось съездить на полугодовое обучение в далекий город Ильменау (Германия), где он успешно (в общем и целом) закончил магистерскую программу Communications and Signal processing. Программа оказалась не из простых, однако сейчас о ней вспоминать даже приятно. Иногда…

Так вот, по окончании этого обучения, кроме диплома, у меня на руках осталось довольно много различных материалов, не поделиться которыми мне показалось неправильным.

Один из таких материалов перед вами.

Какие цели я преследовал, пока готовил семинар:

рассказать о некоторых уже устоявшихся, «умных» подходах в теме антенных решеток наиболее доступно и сделать это на русском языке;
провести небольшое моделирование на языке Python 3, чтобы сагитировать собратьев радиоинженеров присмотреться к языкам программирования (если ещё не присмотрелись);
дать ссылки на хорошую англоязычную литературу — без чтения зарубежных источников, сейчас, увы, никуда.

Что рассмотрим:

Метод MUSIC (MUltiple SIgnal Classification) — к этому, собственно, и отсылка на превью.

Пример по диаграммообразованию и методу MVDR можно найти по ссылке (если по дополнительному материалу будут вопросы или предложения, то обсуждение можно продолжить на Github.Gist).

Как я уже сказал выше, использовать мы будем Python, а именно:

import numpy as np
import matplotlib.pyplot as plt

Почему не MATLAB, один из самых популярных и удобных кандидатов для моделирования с использованием линейной алгебры, спросите вы? Потому что, мне хочется показать, что подобную работу можно сделать и на Python, а сфера применения Python куда шире, чем у MATLAB. Поэтому быть знакомым с синтаксисом Python — дело, на мой взгляд, полезное.

Начнем!

Формулы подготовлены через https://upmath.me/. Спасибо создателям за прекрасный инструмент!

Постановка задачи

Допустим, имеется линейная антенная решетка, состоящая из некоторого количества элементов, разнесенных друг от друга на расстояние $\Delta = \frac{\lambda}{2}$ (шаг антенной решетки), где $\lambda$ — длинна несущей электромагнитной (ЭМ) волны.

На данную антенную решетку с разных направлений падают электромагнитные волны.

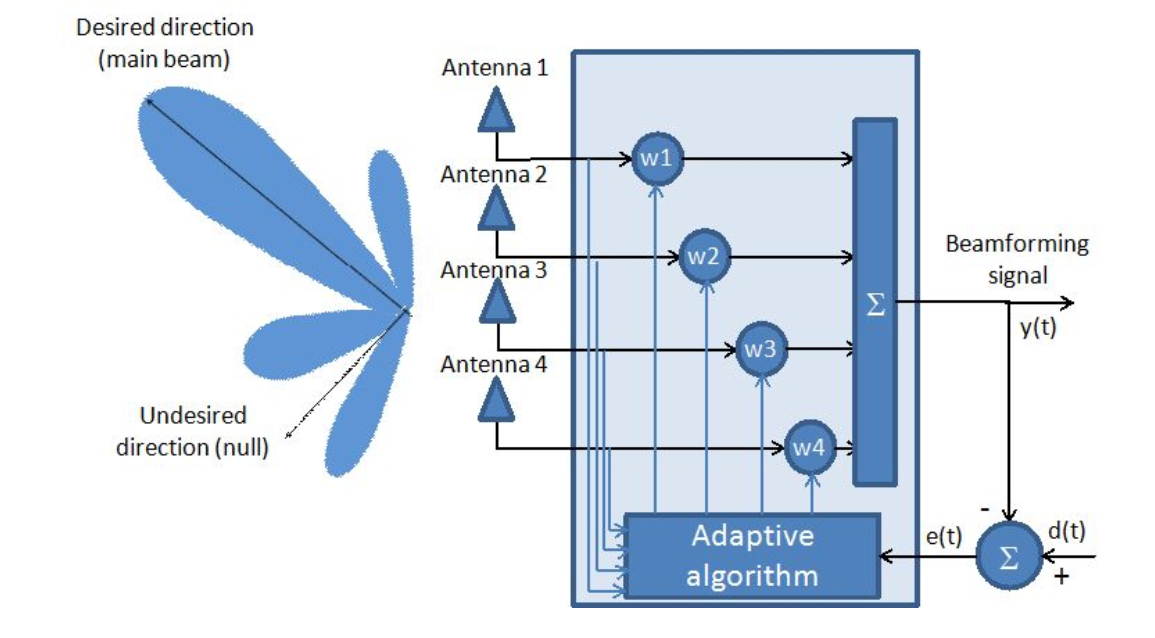
Рис. 1. Адаптивная антенная система.

Как видно из рисунка, антенная решетка рассматривается, как адаптивный фильтр.

Собственно говоря, нахождение оптимального вектора коэффициентов ( $\mathbf{w}_{opt}$ ) и есть основная задача адаптивных антенных решеток с математической точки зрения.

Изначально мы не знаем, с каких именно направлений приходят сигналы и сколько их. Именно для разрешения данного противоречия мы и будем применять алгоритм MUSIC — алгоритм оценки пространственных частот с высоким разрешением.

Моделирование принятого сигнала

Модель принятого сигнала мы можем представить через формулу:

$\mathbf{X} = \mathbf{A} \mathbf{S} + \mathbf{N}$

где $\mathbf{A} = [\mathbf{a}(\theta_1) \quad \mathbf{a}(\theta_2) \quad ... \quad \mathbf{a}(\theta_d)]$ — матрица сканирующих векторов (steering vectors) антенной решетки ( $a_i = \exp(-j \mu m_i)$ , m = 0, 1 ... (M-1) , — количество элементов антенной решетки, — количество источников ЭМ волн, $\theta$ — угол направление прихода ЭМ волны), $\mathbf{S}$ — матрица передаваемых символов, а $\mathbf{N}$ — матрица аддитивных шумов.

ULA

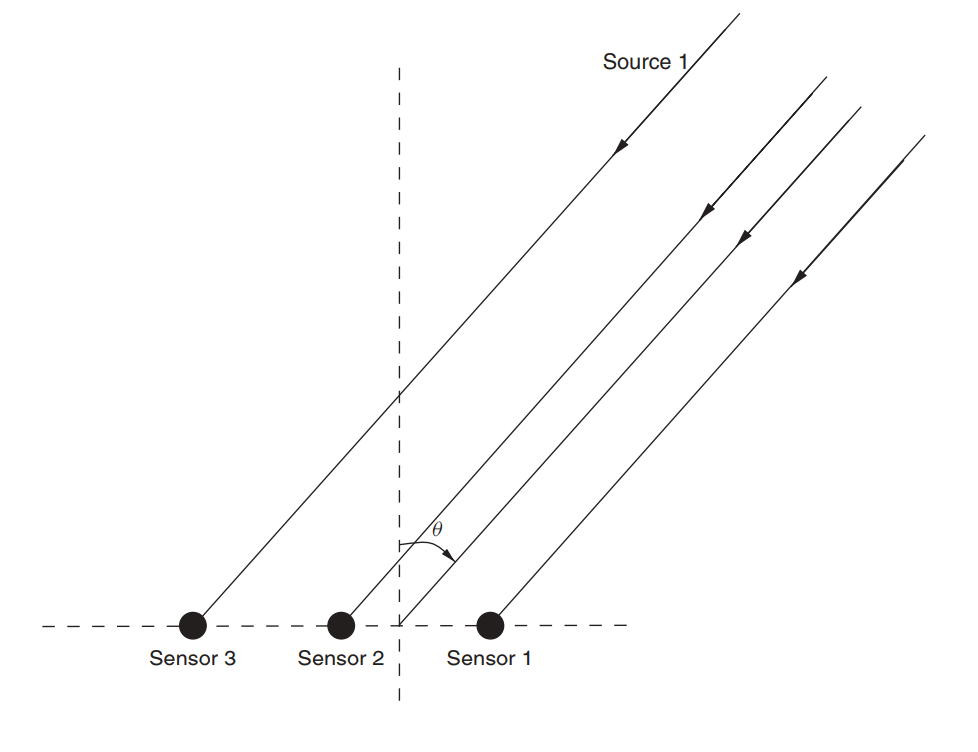
Рис. 2. Ненаправленная линейная антенная решетка (ULAA — uniform linear anntenna array) [1, с. 32].

Переосмыслим данную формулу в «бытовом» ключе: на нашу решетку мы получаем некоторую «кашу» из различных сигналов, которую мы обозначаем через $\mathbf{X}$ . Мы не получаем в явном виде информацию о количестве источников и направлениях, однако, информация об этом всё же содержится в принятом сигнале.

Начинаем искать!

Для этого обычно переходят к манипуляциям не с самими матрицами комплексных амплитуд сигналов, а с их ковариациями (т.е., по сути, с мощностями):

$\mathbf{R}_{xx} = \mathbf{X}\mathbf{X}^H = \mathbf{A} \mathbf{R}_{ss} \mathbf{A}^H + \mathbf{R}_{nn}$

Условия

Введем важное условие к рассмотрению: ограничение углового распознавания по Рэлею (Rayleigh angle resolution limit):

$sin (\theta_R) = \frac{\lambda}{D}$

где $D = M \Delta$ — это длинна линейной решетки.

Переопределим угол прихода электромагнитной волны через понятие пространственной частоты:

$\mu_R = \frac{2 \pi}{\lambda}\Delta sin(\theta_R) = \frac{2 \pi}{\lambda}\Delta \frac{\lambda}{\Delta M} = \frac{2 \pi}{M}$

где $\mu_R$ — есть стандартная ширина главного лепестка ДН (standard beamwidth).

Чтобы проверить насколько наш метод эффективен и при каких условиях, введем некоторые заданные значения для углового разделения:

$\mu_1 = - \mu_R, \quad \mu_2 = 0, \quad \mu_3 = \mu_R \quad$ — разделение в одну ширину луча;
$\mu_1 = -0.5 \mu_R, \quad \mu_2 = 0, \quad \mu_3 = 0.5 \mu_R \quad$ — разделение в одну вторую ширины луча;
$\mu_1 = -0.3 \mu_R, \quad \mu_2 = 0, \quad \mu_3 = 0.3 \mu_R \quad$ — разделение в три десятых ширины луча.

Определим входные параметры:

M = 10 # количество элементов решетки (сенсоров)
SNR = 10 # Отношение сигнал-шум (dB) 
d = 3 # количество источников ЭМ волн
N = 50 # количество "замеров" (snapshots)

S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK

W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN
# Общая формула:
# sqrt(N0/2)*(G1 + jG2), 
# где G1 и G2 - независимые гауссовские процессы.
# т.к. Es(энергия символа) для QPSK равна 1 Вт, спектральная мощность шума (noise spectral density): 
# N0 = (Es/N)^(-1) = SNR^(-1) [Вт] (принимаем в данном примере, что SNR = Es/N0); 
# или в логарифмическом масштабе:
# SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB [дБ]; 
# Нам дано значение SNR в логарифмической шкале (т.е. в дБ), переводим в линейную:
# SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) 

mu_R = 2*np.pi / M

Немного теории о самом методе

Прежде всего отметим, что прародителем метода MUSIC является метод Писаренко (1973). Рассматриваемая задача метода Писаренко заключалась в оценке частот суммы комплексных экспонент в белом шуме. В.Ф. Писаренко продемонстрировал, что частоты можно найти из собственных векторов, соответствующих минимальному собственному значению автокорреляционной матрицы. Впоследствии этот метод стал особым случаем метода MUSIC. [2, c. 459]

Шмидт со своими коллегами предложил алгоритм классификации множественных сигналов (MUSIC) в 1979 году [4]. Основным подходом этого алгоритма является разложение матрицы ковариации принятого сигнала на собственные значения. Поскольку этот алгоритм учитывает некоррелированный шум, порожденная ковариационная матрица имеет диагональный вид. Здесь подпространства сигнала и шума вычисляются с использованием линейной алгебры, и являются ортогональными друг другу. Поэтому алгоритм использует свойство ортогональности для выделения сигнальных и шумовых подпространств [5].

Обобщенный алгоритм MUSIC можно определить следующим образом:

Найти ковариационную матрицу $\mathbf{R}_{xx}$
Найти собственные вектора через EVD или же другой подходящий числовой алгоритм:

$\mathbf{R}_{xx} = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^H \qquad(1)$

Найти псевдоспектр (почему с приставкой псевдо, мы обсудим ниже) MUSIC через следующую формулу:

$P_{MU}(e^{j\omega}) = \frac{1}{\sum \limits_{i=d+1}^{M}|\mathbf{a}^H\mathbf{u}_i|^2} \qquad(2)$

где $\mathbf{a} = \begin{bmatrix} e^{j0\omega} & e^{j1\omega} & e^{j2\omega} & ... & e^{j(M-1)\omega} \end{bmatrix}^T$ — вектор экспонент для частоты ω, лежащей в некотором заданном диапазоне, а $\mathbf{u}_i$ — i-ый собственный вектор (eigen vector) ковариационной матрицы (1), соответствующие шумовому подпространству матрицы (1) — отсюда и индексация с d+1 ( — ранг матрицы (1)).

Для большей наглядности попробуйте прогнать соответствующий MATLAB-скрипт представленный по ссылке. Обратите внимание на два основных момента:

вместо вычисления квадрата второй нормы в знаменателе (2) авторы применяют к собственным векторам алгоритм БПФ, что облегчает моделирование за счет применения встроенных функций и, в общем, не противоречит теории с математической точки зрения;

вычисление ковариационной матрицы производится через сверточные матрицы, выше для оценки пространственных частот был показан другой подход.

Как нетрудно догадаться из названия, MUSIC также является классическим методом оценки направления приема с высоким разрешением. Алгоритм вычисления псевдоспектров в данном контексте приведем ниже:

$\mathbf{U} = [\mathbf{U}_s \quad \mathbf{U}_0]$

выбираем некоторый диапазон поиска:

$a(\mu) = \begin{bmatrix} e^{j0\mu_1} & ... & e^{j0\mu_Q} \\ ... &...&... \\ e^{j(M-1)\mu_1} & ... & e^{j(M-1)\mu_Q} \end{bmatrix}$

где $\mu = -\frac{2\pi f_c}{c}\Delta sin\theta = -\frac{2\pi }{\lambda }\Delta sin\theta$

вычисляем псевдоспектр:

$P_{MU}(\theta)=\frac{\mathbf{a}^H (\theta)\mathbf{a}(\theta)}{\mathbf{a}^H(\theta)\mathbf{U}_0 \mathbf{U}_0^H \mathbf{a}(\theta)}$

Связь между спектральным анализом и анализом углов прихода (DoA — direction of arriaval) ЭМ волн описана в таблице 1.

Таблица 1 Связь между приложениями MUSIC: Обработка массива сигналов и Гармонический поиск [6].

Переменная	Обработка массива сигналов	Гармонический поиск
	Количество сенсоров	Количество временных отрезков
	Количество временных отрезков	Количество экспериментов
	Количество волновых фронтов	Количество комплексных компонент
$\mu$	Пространственные частоты	Нормализованные частоты

В общем и целом, процесс приема через массивы (решетки) можно сравнить с процессом классической дискретизации, т.к. в сущности каждый сенсор, принимая волну с определенной задержкой фазы (т.е. с определенной временной задержкой), выполняет функции дискретизирующего дельта импульса. Количеству реализаций (экспериментов) классического спектрального анализа будет соответствовать количество временных отрезков (snapshots). Каждому источнику будет соответствовать свой волновой фронт, что эквивалентно количеству уникальных синусоид сигнала в случае спектрального анализа.

А теперь вернемся к моменту вычисления собственных векторов. Мы уже упомянули выше, что вектора $a(\theta_i)\epsilon A$ , где i=1,2,..,d ортогональны шумовому подпространству ковариационной матрицы, т.е.:

$a(\theta_i)^TU_0=0^T$

Собственно говоря, мы видим систему уравнений, решая которую мы можем найти корни — собственные вектора. Такой метод в отличие от числовых алгоритмов (к которым, как мы отметили выше, относится и EVD) позволяет получить настоящие, а не приближенные собственные значения. Именно поэтому данный подход позволяет получить не псевдоспектр, а спектр. Эта же идея легла в основу алгоритма Root MUSIC.

Моделирование

Фуф! Наконец-то все формулы описаны и сколько-то объяснены. Можем приступать к моделированию.

cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],]
for idxm, c in enumerate(cases):
    # углы прихода (пространственные частоты):
    mu_1 = c[0]*mu_R
    mu_2 = c[1]*mu_R
    mu_3 = c[2]*mu_R

    # сканирующие вектора
    a_1 = np.exp(1j*mu_1*np.arange(M))
    a_2 = np.exp(1j*mu_2*np.arange(M))
    a_3 = np.exp(1j*mu_3*np.arange(M))

    A = (np.array([a_1, a_2, a_3])).T # матрица сканирующих векторов
    X = np.dot(A,S) + W # матрица принятых сигналов

    R = np.dot(X,np.matrix(X).H)

    U, Sigma, Vh = np.linalg.svd(X, full_matrices=True)
    U_0 = U[:,d:] # шумовое подпространство

    thetas = np.arange(-90,91)*(np.pi/180) # диапазон азимутов
    mus = np.pi*np.sin(thetas) # диапазон пространственных частот
    a = np.empty((M, len(thetas)), dtype = complex)

    for idx, mu in enumerate(mus):
        a[:,idx] = np.exp(1j*mu*np.arange(M))

    # MVDR:
    S_MVDR = np.empty(len(thetas), dtype = complex)
    for idx in range(np.shape(a)[1]):
        a_idx =  (a[:, idx]).reshape((M, 1))
        S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx)))

    # MUSIC:
    S_MUSIC = np.empty(len(thetas), dtype = complex)
    for idx in range(np.shape(a)[1]):
        a_idx =  (a[:, idx]).reshape((M, 1))
        S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\
        / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx))))

    plt.subplots(figsize=(10, 5), dpi=150)
    plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR')
    plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC')
    plt.grid(color='r', linestyle='-', linewidth=0.2)
    plt.xlabel('Azimuth angles θ (degrees)')
    plt.ylabel('Power (pseudo)spectrum (normalized)')
    plt.legend()
    plt.title('Case #'+str(idxm+1))
    plt.show()

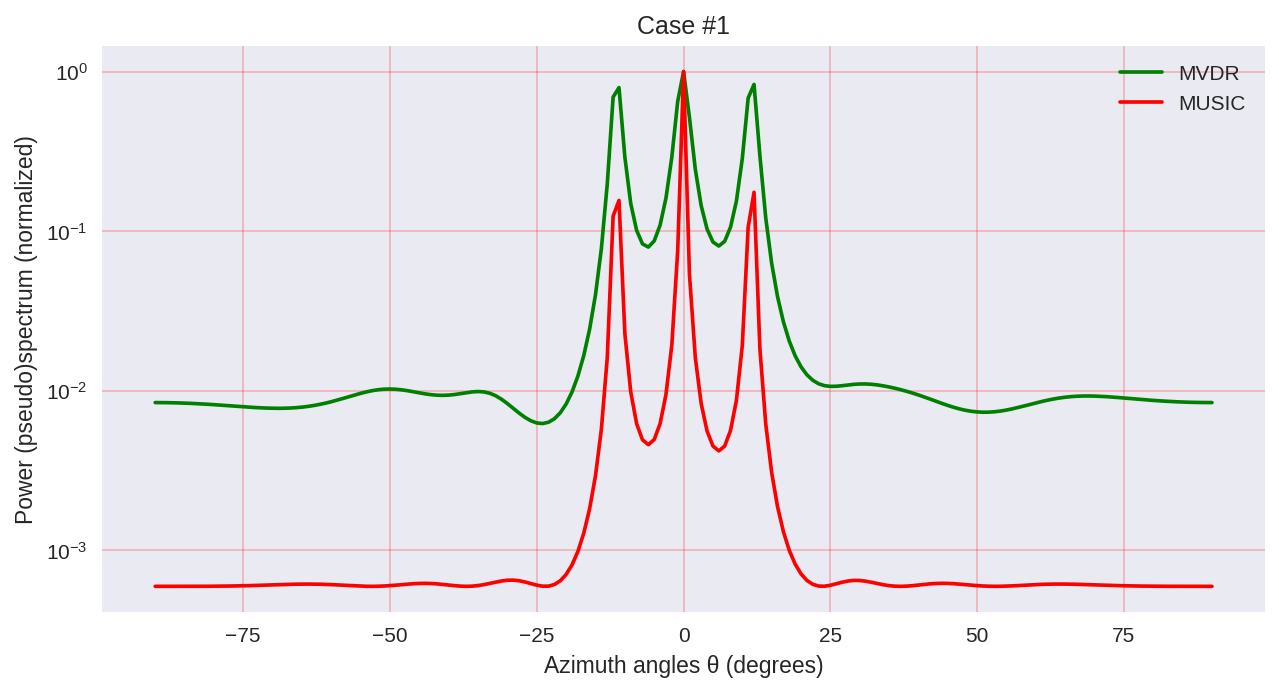
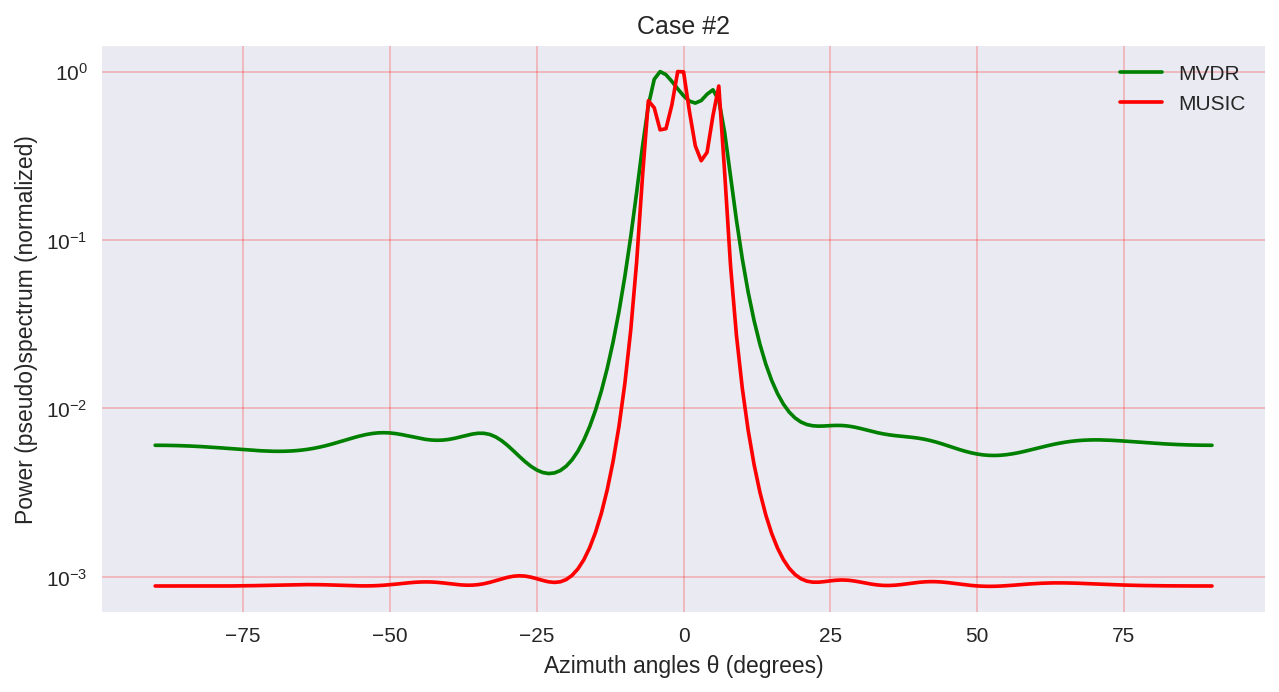
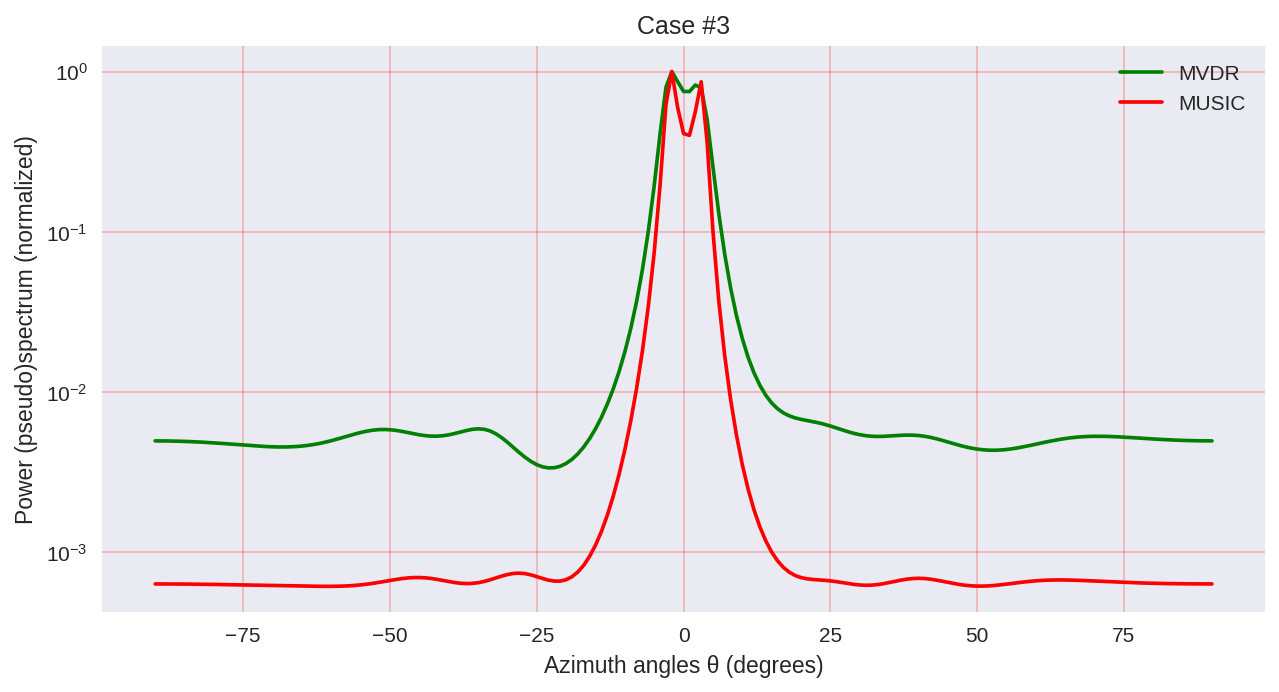
Как мы можем заметить, MUSIC обладает большей разрешающей способностью и позволяет добиться, в целом, лучших результатов, чем, например, позволяет MVDR — такой же представитель параметрических методов спектрального анализа.

Однако нужно учитывать, что при использовании MUSIC мы задействуем более дорогие в вычислительном плане алгоритмы, такие как EVD или SVD, что является некоторой ценой за большую точность.

Такие дела.

Список использованной литературы:

Haykin, Simon, and KJ Ray Liu. Handbook on array processing and sensor networks. Vol. 63. John Wiley & Sons, 2010. pp. 102–107
Hayes M.H. Statistical digital signal processing and modeling. — John Wiley & Sons, 2009.
Haykin, Simon S. Adaptive filter theory. Pearson Education India, 2008. pp. 422–427
Richmond, Christ D. «Capon algorithm mean-squared error threshold SNR prediction and probability of resolution.» IEEE Transactions on Signal Processing 53.8 (2005): 2748–2764.
S.K. P. Gupta, MUSIC and improved MUSIC algorithm to esimate dorection of arrival, IEEE, 2015.
Professor Martin Haardt’s lectures (array array)