[Из песочницы] Минимализм в криптографии, или схема Even–Mansour28.08.2015 12:03

Израильские ученые Шиман Ивэн (Shimon Even) и Ишэй Мансур (Yishay Mansour) еще в 1997 году задались вопросом: насколько минимальной конструкцией может обладать стойкий блочный шифр? Под минимальностью они подразумевали число конструктивных элементов в схеме шифра, а под стойкостью — любую (формально верную) оценку снизу сложностей атак на этот шифр. Как говорится, под катом — описание минимального (и по сей день) блочного шифра с доказуемой стойкостью.

Лирическое отступление

Практически все стандарты шифрования, используемые сегодня, не являются формально стойкими. Никто не дает, и не может дать никаких гарантий, что в них нет закладок, уязвимостей или слабостей. Просто до сих никто не придумал (или, по крайней мере, не опубликовал) никаких способов взломать эти шифры = способов существенно снизить экспоненциальную сложность полного перебора. Вскрытие практически любых криптографических алгоритмов, на которых зиждятся ваши безопасность и конфиденциальность, будь то симметричное, асимметричное шифрование, или хэширование, сводится к решению относительно сложных задач (например, к задаче дискретного логарифмирования). Сложных потому, что относительно простых решений до сих пор никто не предложил. Пока мы не научимся логарифмировать в конечном поле или разлагать числа на множители за полиномиальное время (или пока не построим квантовый компьютер побольше), DH и RSA будут считаться стойкими, и только число бит в ключе будет расти пропорционально мощности персональных компьютеров.

А все потому, что мы пока не умеем получать оценок снизу. Друзья, в математике (и особенно в криптографии) не так много красивых идей и изящных решений, а доказанных оценок снизу — еще меньше. Рассмотренный здесь шифр, на мой взгляд, попадает в пересечение: он максимально прост, и в то же время формально стоек.

Предупреждаю сразу, что эта публикация — не художественное произведение для неподготовленных читателей, хотя и не содержит ничего более сложного, чем формулу условной вероятности Байеса и элементарную арифметику дробей. Неискушенный читатель останется удовлетворенным и описанием конструкции шифра, а строгое доказательство его стойкости приведено здесь для специалистов и истинных ценителей математики.

Израильские ученые Шиман Ивэн (Shimon Even) и Ишэй Мансур (Yishay Mansour) в [EM97] предложили способ построить блочный шифр, обладающий доказуемой стойкостью, на основе единственной случайно выбранной подстановки из $S_{2n}$ .

Прежде, чем я познакомлю вас непосредственно с этим блочным шифром, позволю себе указать список введенных условных обозначений и базовых определений. Впрочем, вы всегда сможете к нему вернуться, поэтому, в том случае, если мне удалось пробудить в вас нешуточный интерес увидеть все «здесь и сейчас», переходите непосредственно к описанию шифра.

Определения и условные обозначения

Израильские ученые Шимон Ивэн (Shimon Even) и Ишай Мансур (Yishay Mansour) в своей работе предложили блочный шифр c доказуемой криптостойкостью, для которого требуется всего одна подстановка $\pi$ , которая случайным (или псевдослучайным) образом выбирается из множества всех перестановок $S_{2^n}$ над открытыми текстами.

При этом предполагается, что выбранная подстановка не является частью ключа, и доступна любому атакающему в виде некоторого «черного ящика».

Утверждается, что, с точки зрения атакующего, предложенный шифр практически неотличим от идеального случайного шифра, и вероятность успешного вскрытия системы (восстановления секретного ключа $\underline{K}$ ) полиномиально мала (основной результат — Теорема 2, Следствие 2.1 из нее, и Теорема 3).

Утверждается также, что использование псевдослучайной подстановки вместо истинно случайной подстановки не изменяет показанной стойкости шифра.

Описание

Пусть $\mathcal{P} \equiv \mathcal{C}$ , и $\pi \in S_{\left\vert\, {\mathcal{P} \,\right\vert}$ — подстановка, выбранная из множества $S_{\left\vert\, {\mathcal{P} \,\right\vert}$ всех подстановок над множеством открытых текстов, а $\pi^{-1}$ — обратная к ней.

Предполагается, что для любых элементов $P \in \mathcal{P}$ и $C \in \mathcal{C}$ множеств открытых и шифртекстов значения $\pi(P)$ и $\pi^{-1} (C)$ могут быть легко получены либо с помощью непосредственного вычисления значения подстановок $\pi$ и $\pi^{-1}$ , либо посредством обращения к общедоступным оракулам $\mathrm{P}_{\pi}$ и $\mathrm{P}^{-1}_{\pi}$ .

Пространства открытых и шифртекстов являются пространствами двоичных $n$ –мерных векторов: $\mathcal{P} \equiv \mathcal{C} = \left\lbrace 0, 1 \right\rbrace^n = \mathbb{Z}_{2}^{n}$ , а пространство ключей системы является пространством двоичных векторов размерности $2n$ : $\mathcal{K} = \left\lbrace 0,1 \right\rbrace^{2n} = \mathbb{Z}_{2}^{2n}$ .

Секретный ключ $\underline{K} \in \mathcal{K}$ является упорядоченной парой двух $n$ –мерных подключей (половин) $\underline{K}_1$ и $\underline{K}_2$ ; каждый подключ выбирается случайно из пространства $n$ –мерных двоичных векторов с равной вероятностью $2^{-n}$ .

Предполагается также, что выбранный секретный ключ $\underline{K}$ известен только легитимным пользователям, и используется ими для шифрования открытых текстов (сообщений) и расшифрования шифртекстов (криптограмм).

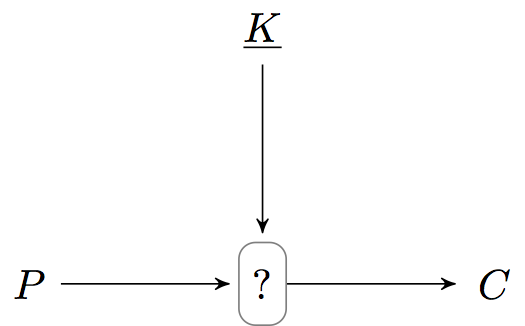
Шифрование открытого текста $P$ с помощью секретного ключа $\underline{K} = \left\langle \underline{K}_1, \underline{K}_2 \right\rangle$ и выбранной подстановки $\pi$ производится следующим образом:

$E_{\underline{K}} (P) = E(P, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle) = \pi(P \oplus \underline{K}_1) \oplus \underline{K}_2,$

а расшифрование шифртекста $C$ с помощью ключа $K$ и выбранной подстановки $\pi$ — следующим:

$D_{\underline{K}} (C) = D(C, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle) = \pi^{-1}(C \oplus \underline{K}_2) \oplus \underline{K}_1.$

Действительно, просто? Взяли сообщение, поксорили с первой половиной ключа, по открытой и доступной всем табличке заменили, поксорили со второй половиной ключа, и получилась криптограмма. Здорово, правда? Почему же никто не использует эту схему на практике? Ведь она намного проще AES, да и DES. Самый простой блочный шифр. Где здесь подвох?

Подвох

Все дело в том, подстановка задана на двоичных $n$ –битных векторах, и хранить таблицу замены для случайно выбранной подстановки совершенно неприемлимо, на это потребуется $\mathcal{O}\!\left(2^n\right)$ памяти. Единственно возможное решение этой проблемы заключается в том, чтобы строить хорошие псевдослучайные подстановки (полиномиально неотличимые от случайных), значения которых можно было бы относительно легко вычислить в любой точке;, а это мы пока не умеем.

О минимальности схемы

Следует отметить, что классическая схема минимальна в том смысле, что удаление любого из элементов этой схемы приводит к значительному ослаблению ее стойкости. Легко показать, что удаление любого из сложений с подключами, либо подстановки $\pi$ сделает схему уязвимой, и, как следствие, совершенно нестойкой.

О стойкости схемы

Предположения стойкости, определения

Стойкость предложенной схемы обусловлена следующими предположениями:

злоумышленнику не известен истинный ключ $\underline{K} \in \mathcal{K}$ ;
злоумышленник имеет возможность шифровать открытые тексты (сообщения) и расшифровывать шифртексты (криптограммы) на секретном ключе $\underline{K}$ ;
злоумышленник имеет возможность вычислять значения перестановки $\pi$ и обратной к ней перестановки $\pi^{-1}$ .

Всякий алгоритм, вскрывающий систему, может обращаться к следующим четырем оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ :

оракул $\mathrm{P}_{\pi}$ вычисляет значение перестановки $\pi \in S_{\left\vert\,\mathcal{P}\right\vert\,}$ на $n$ –мерном двоичном входном наборе $M$ :

$\mathrm{P}_{\pi} \colon \mathbb{Z}_{2}^{n} \mapsto \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{P}_{\pi}}\left[M\right]} = \pi (M);$

оракул $\mathrm{P}^{-1}_{\pi}$ вычисляет значение перестановки $\pi^{-1} \in S_{\left\vert\,\mathcal{P}\,\right\vert}$ на $n$ –мерном двоичном входном наборе $M'$ :

$\mathrm{P}^{-1}_{\pi} \colon \mathbb{Z}_{2}^{n} \mapsto \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{P}^{-1}_{\pi}}\left[M'\right]} = \pi^{-1} (M');$

$\mathrm{E}_{\underline{K}, \pi} \colon \mathcal{P} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{C} \equiv \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{E}_{\underline{K}, \pi}}\left[P\right]} = \underline{K}_2 \oplus \pi (P \oplus \underline{K}_1);$

$\mathrm{D}_{\underline{K}, \pi} \colon \mathcal{C} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{P} \equiv \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{D}_{\underline{K}, \pi}}\left[C\right]} = \underline{K}_1 \oplus \pi^{-1} (C \oplus \underline{K}_2).$

Далее, если подстановка, значение которой вычисляет оракул $\mathrm{P}_{\pi}$ ( $\mathrm{P}^{-1}_{\pi}$ ), выбрана, а шифрование и расшифрование осуществляется на фиксированном ключе $\underline{K}$ , то индекс у обозначений оракулов мы будем опускать: $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Обращаясь к оракулам $\mathrm{P}$ и $\mathrm{P}^{-1}$ с запросами на вычисление значения подстановок $\pi$ и $\pi^{-1}$ в точках $M$ и $M' = \pi(M)$ , алгоритм получает ответы $M'$ и $M$ соответственно.
Таким образом, общение всякого алгоритма с оракулами $\mathrm{P}$ и $\mathrm{P}^{-1}$ сводится к формированию пар вида «точка», «значение подстановки $\pi$ в этой точке»:

$\left\langle M, M' \right\rangle = \left\langle M, \pi(M) \right\rangle.$

Назовем такие пары $P$ –парами, а набор всех $P$ –пар, выработанных некоторым алгоритмом $\mathrm{A}$ в результате его выполнения, обозначим через $\mathsf{P}_{\mathrm{A}}$ , или просто $\mathsf{P}$ .

Обращаясь к оракулам $\mathrm{E}$ и $\mathrm{D}$ с запросами на шифрование открытого текста $P$ и расшифрование шифртекста $C = E(P, \underline{K})$ , алгоритм получает ответы $C$ и $P$ соответственно.
Так, общение всякого алгоритма с оракулами $\mathrm{E}$ и $\mathrm{D}$ сводится к формированию пар вида «открытый текст», «шифртекст»:

$\left\langle P, C \right\rangle = \left\langle M, E(P, \underline{K \right\rangle)}.$

Назовем такие пары $E$ –парами, а набор всех $E$ –пар, выработанных некоторым алгоритмом $\mathrm{A}$ в результате его выполнения, обозначим через $\mathsf{E}_{\mathrm{A}}$ , или просто $\mathsf{E}$ .

Определение
$E$ –пары $\left\langle P_1, C_1 \right\rangle$ и $\left\langle P_2, C_2 \right\rangle$ называются пересекающимися, если $P_1 = P_2$ , либо $C_1 = C_2$ .

Аналогичное определение можно сформулировать и для $P$ –пар.

Определение
$P$ –пары $\left\langle M_1, M_1' \right\rangle$ и $\left\langle M_2, M_2' \right\rangle$ называются пересекающимися, если $M_1 = M_1'$ , либо $M_2 = M_2'$ .

Утверждение 1 (Overlapping pairs are identical)
Ввиду того, что все оракулы $\mathrm{P}_{\sigma}, \mathrm{P}^{-1}_{\sigma}, \mathrm{E}_{K, \sigma}, \mathrm{D}_{K, \sigma}$ честны, для любых фиксированных $\sigma$ и $K$ справедливы утверждения:

пересекающиеся $E$ –пары совпадают;
пересекающиеся $P$ –пары совпадают.

По модулю утверждения 1 можно полагать, что все пары множеств $\mathsf{E}$ и $\mathsf{P}$ не пересекаются между собой.

Вероятностью успеха $p_{\mathrm{A}}$ алгоритма $\mathrm{A}$ назовем вероятность вычисления этим алгоритмом $\mathrm{A}$ корректного выхода на произвольных (но корректных) входах. Так, например, вероятностью $p_{\mathrm{A}}$ успеха алгоритма $\mathrm{A}$ , вычисляющего ключ шифрования по $E$ –паре $\left\langle P, C \right\rangle$ , будет вероятность

$\forall P, C \>\Longrightarrow\> p_{\mathrm{A}} = \Pr{\operatorname{A}\left[\left\langle P, C \right\rangle\right]} = \underline{K}}.$

Под временем выполнения $T_{\mathrm{A}}$ алгоритма $\mathrm{A}$ будем понимать число запросов, выполненных этим алгоритмом к оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Определение
Функция $f(n) \colon \mathbb{N}_0 \mapsto \left[ 0, 1 \right]$ называется полиномиально мaлой (polynomially negligable), если для любого полинома $p(n)$ найдется $n_0$ , такое, что для всех $n > n_0$ выполняется $f(n) < 1 / p(n)$ :

$f(n) \text{ is polynomially negligable} \iff \exists n_0 \mid \forall n > n_0 \>\Longrightarrow\> f(n) < \frac{1}{p(n)}.$

Определение
Задачу $\mathsf{T}$ назовем трудной, если вероятность успеха любого решающего ее алгоритма, полиномиально ограниченного по времени, полиномиально мала.

Описание формальной модели

В предложенной в [EM97] модели злоумышленник в полном объеме обладает знаниями об устройстве шифра и выбранной подстановке $\pi$ . Для вскрытия системы злоумышленник использует некоторый алгоритм $\mathrm{A}$ , который может решать одну из двух задач: задачу дешифрования $\mathsf{CP}$ , или задачу построения новой пары открытый текст / шифртекст $\mathsf{EFP}$ .

Задача дешифрования ( $\mathsf{CP}$ )

Под задачей дешифрования (
$\mathsf{CP}$ , cracking problem) понимается проблема дешифрования злоумышленником некоторого закрытого текста $C_0$ . При этом всякий алгоритм $\mathrm{A}$ , используемый злоумышленником для решения задачи, может обращаться к оракулам $\mathrm{P}$ , $\mathrm{P}^{-1}$ , $\mathrm{E}$ , $\mathrm{D}'$ , где:

$\mathrm{D}_{\underline{K}, \pi}' \colon \mathcal{C} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{P} \equiv \mathbb{Z}_{2}^{n}, \quad \mathrm{D}_{\underline{K}, \pi}' \left[ C \right] = \underline{K}_1 \oplus \pi^{-1} (C \oplus \underline{K}_2) \text{ with } C \neq C_0.$

Алгоритм $\mathrm{A}$ успешно вскрывает систему, если $\operatorname{A}\left[C_0\right]} = D (C_0, \underline{K})$ .

Задача построения новой пары открытый текст / шифртекст ( $\mathsf{EFP}$ )

Под задачей построения новой пары текстов ( $\mathsf{EFP}$ , existential forgery problem) понимается проблема построения такой пары $\left\langle P, C \right\rangle$ , которая бы удовлетворяла соотношению $C = E(P, \underline{K})$ , и при этом не состояла из запроса и ответа к одному из оракулов $\mathrm{E}, \mathrm{D}$ . При этом всякий алгоритм $\mathrm{B}$ , используемый злоумышленником для решения задачи, может обращаться ко всем четырем оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Успехом алгоритма $\mathrm{B}$ считается получение новой корректной пары открытого текста и шифртекста $\left\langle P, C \right\rangle$ .

Сведение задачи построения пары текст / шифртекст к задаче вскрытия ( $\mathsf{EFP} \varpropto \mathsf{CP}$ )

Теорема 1 (EFP to CP reduction)
Пусть $n \in \mathbb{N}$ , и существует алгоритм $\mathrm{A}$ , решающий задачу вскрытия $\mathrm{CP}$ за время $T(n)$ с вероятностью успеха $\xi(n)$ , тогда существует алгоритм $\mathrm{B}$ , строящий пару текстов $\left\langle P, C \right\rangle$ за то же самое время $T(n)$ с вероятностью успеха $\xi(n) / T(n)$ :

$\exists \mathrm{A} \text{ для решения } \mathsf{CP} \mid T_{\mathrm{A}} = T(n),\ p_{\mathrm{A}} = \xi(n) \>\Longrightarrow\> \exists \mathrm{B} \text{ для решения } \mathsf{EFP} \mid T_{\mathrm{B}} \leq T(n),\ p_{\mathrm{B}} = \frac{\xi(n)}{T(n)}.$

Доказательство

Зафиксируем открытый текст $P_0$ , ключ $\underline{K}$ и шифртекст $C_0 = E (P_0, \underline{K})$ , и рассмотрим ход выполнения алгоритма $\operatorname{A}\left[C_0\right]}$ .

Без ограничения общности можно полагать, что, если алгоритм $\mathrm{A}$ успешно дешифрует $C_0$ , то в некоторый критический момент времени $T' < T(n)$ выполнения этого алгоритма злоумышленник проверяет найденный открытый текст, –, кандидат $P_0$ , отправив (впервые) запрос на его шифрование к оракулу $\mathrm{E}$ и сравнив дешифруемый шифртекст $C_0$ с ответом оракула:

$\operatorname{E_K}\left[P_0\right]} \stackrel{?}{=} C_0.$

На основании алгоритма $\mathrm{A}$ построим алгоритм $\mathrm{B}$ , решающий задачу $\mathsf{EFP}$ :

Зафиксируем шифртекст $C_0 \in \mathcal{C}$ ;
Начнем выполнение алгоритма $\operatorname{A}\left[C_0\right]}$ ;
Выберем случайное $\tau$ , распределенное равномерно на отрезке $\left[1, t(n)\right]$ ;
Остановим выполнение алгоритма $\operatorname{A}\left[C_0\right]}$ после $\tau - 1$ запросов к оракулам;
Если в запросе $\tau$ алгоритм $\operatorname{A}\left[C_0\right]}$ запрашивает шифрование $P'$ , то выполнение алгоритма прекращается, и исходная пара — $\left\langle P', C_0 \right\rangle$ .

Легко видеть, что алгоритм $\mathrm{B}$ осуществляет не более $T(n)$ запросов к оракулам $\mathrm{E}, \mathrm{D}$ , при этом искомая пара $\left\langle P', C_0 \right\rangle$ будет построена только в том случае, если алгоритм дешифрования $\mathrm{A}$ успешно дешифрует текст $C_0$ (с вероятностью $p_{\mathrm{A}} = \xi(n)$ ) и $\mathrm{A}$ будет остановлен в критический момент времени $T'$ (с вероятностью $1 / T(n)$ ):

$p_{\mathrm{B}} = p_{\mathrm{A}} \cdot \frac{1}{T(n)} = \frac{\xi(n)}{T(n)},$

что и требовалось доказать.

Следствие 1.1
Пусть задача $\mathsf{EFP}$ трудна (для любого полиномиального решающего алгоритма $\mathrm{B}$ его вероятность успеха $p_{\mathrm{B}}$ полиномиально мала), тогда задача $\mathsf{CP}$ тоже трудна (для любого полиномиального решающего алгоритма $\mathrm{A}$ его вероятность успеха $p_{\mathrm{A}}$ полиномиально мала).

Следует заметить, что обратное утверждение (сводимость $\mathsf{CP} \varpropto \mathsf{EFP}$ ) не верно в общем случае: в некоторых классах криптосистем существуют открытые тексты, такие, что соответствующие им шифртексты заранее известны и не зависят от ключа (например, $P = 1$ в схеме RSA).

Стойкость системы при использовании случайной подстановки $\pi$

Основные идеи доказательства стойкости заключаются в следующем:

показать, что на любом этапе полиномиально ограниченной атаки, множество «хороших» ключей (ключей, истинность которых злоумышленник ни подтвердить, ни опровергнуть на основе имеющихся у него данных) экспоненциально велико (Лемма 1);
показать, что злоумышленник может «угадать» истинный ключ $\underline{K}$ только с полиномиально малой вероятностью (Теорема 2);
показать, что злоумышленник собрать достаточно данных для выявления истинного ключа $\underline{K}$ за полиномиальное число запросов к оракулам (Теорема 2).

Определение
Первый подключ $K_1$ ключа $K = \left\langle K_1, K_2 \right\rangle$ называется плохим относительно алгоритма $\mathrm{A}$ и выработанных им множеств $\mathsf{E}$ и $\mathsf{P}$ , если существуют $E$ –пара $\left\langle P_i, C_i \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P}$ , такие, что $P_i \oplus K_1 = M_j$ ; и хорошим в другом случае:

$K_1 \text{ is a bad key} \iff \exists \left\langle P_i, C_i \right\rangle \in \mathsf{E}, \left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P} \>\Longrightarrow\> P_i \oplus K_L = M_j.$

Другими словами, подключ $K_1$ будем считать хорошим, если на основе материала, полученного в результате выполнения алгоритма $\mathrm{A}$ невозможно выяснить, является ли $K_1$ подключом истинного ключа $\underline{K}$ . Поясним это неформальное определение следующим примером: пусть подключ $K_1$ является плохим, тогда, согласно определению плохого подключа, найдутся $E$ –пара $\left\langle P_i, C_i \right\rangle,$ где $C_i = E(P_i, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle)$ , и $P$ –пара $\left\langle P_i \oplus K_1, \pi (P_i \oplus K_1) \right\rangle$ . Тогда ключ $K = \left\langle K_1, K_2 \right\rangle$ является кандидатом на роль истинного ключа $\underline{K}$ , где

$K_2 = C_i \oplus \left( \pi (P_i \oplus K_1) \right).$

Очевидно, такой ключ $K = \left\langle K_1, K_2 \right\rangle$ удовлетворяет этой $E$ –паре, ведь

$E(P_i, K) = K_2 \oplus \pi (K_1 \oplus P_i) = \big( C_i \oplus (\pi (P_i \oplus K_1))\big) \oplus \pi (K_1 \oplus P_i) = C_i.$

С помощью других собранных $E$ –пар и $P$ –пар злоумышленник имеет возможность проверить, является ли построенный таким образом ключ $K$ истинным ключом $\underline{K}$ вскрываемой системы; и принять (в качестве подключа $\underline{K}_1$ ), либо отбросить подключ $K_1$ .

Аналогичное определение можно сформулировать и для вторых подключей $K_2$ .

Определение
Второй подключ $K_2$ ключа $K = \left\langle K_1, K_2 \right\rangle$ называется плохим относительно алгоритма $\mathrm{A}$ и выработанных им множеств $\mathsf{E}$ и $\mathsf{P}$ , если существуют $E$ –пара $\left\langle P_i, C_i \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P}$ , такие, что $C_i \oplus K_2 = \pi(M_j)$ ; и хорошим в другом случае:

$K_2 \text{ — плохой} \iff \exists \left\langle P_i, C_i \right\rangle \in \mathsf{E}, \left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P} \>\Longrightarrow\> C_i \oplus K_2 = \pi(M_j).$

Определение
Ключ $K = \left\langle K_1, K_2 \right\rangle$ называется хорошим, если оба подключа $K_1$ и $K_2$ являются хорошими, и плохим в другом случае.

Утверждение 2 (True subkeys share goodness)
При секретном ключе $\underline{K} = \left\langle \underline{K}_1, \underline{K}_2 \right\rangle$ и перестановке $\pi$ подключи $\underline{K}_1$ и $\underline{K}_2$ либо оба являются хорошими, либо плохими:

$\underline{K}_1 \text{ is a good key} \iff \underline{K}_2 \text{ is a good key} \quad (\text{when } \underline{K}, \pi \text{ are fixed}).$

Лемма 1 (The fraction of bad keys)
Пусть алгоритм $\mathrm{A}$ выработал множества $\mathsf{E}, \left\vert\,{\mathsf{E}\,\right\vert = l$ и $\mathsf{P}, \left\vert\,{\mathsf{P}\,\right\vert = m$ непересекащихся $E$ –пар и $P$ –пар соответственно, тогда доля $Q$ плохих ключей в ключевом пространстве $\mathcal{K}$ не превышает $2lm / 2^n$ .

Доказательство

Согласно определению плохого подключа, некоторый подключ $K_1$ является плохим, если найдется $E$ –пара $\left\langle P_{i}, C_{i} \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_{j}, \pi(M_{j})\right\rangle \in \mathsf{P}$ , такие, что

$P_{i} \oplus K_1 = M_{j}, \text{ или } K_1 = P_{i} \oplus M_{j}.$

В крайнем случае, последнее равенство может выполниться для всех наборов $i, j$ , тогда, при различных $P_{i} \mid 1 \leq i \leq l$ и $M_{j} \mid 1 \leq j \leq m$ , все $\left\vert\,\mathsf{E}\,\right\vert \cdot \left\vert\,\mathsf{P} \,\right\vert = l \cdot m$ подключей $K_1$ являются плохими.

Аналогичные рассуждения приводят к тому, что наибольшее число плохих подключей $K_2$ тоже не превышает $lm$ .

Оба подключа выбираются из $\mathbb{Z}_{2}^{n}$ , что позволяет получить верхние оценки для числа плохих ключей:

$\# \left\lbrace K \text{ is a bad key} \right\rbrace \leq lm \cdot 2^n + lm \cdot 2^n = 2 lm 2^n,$

и доли плохих ключей в ключевом пространстве $\mathcal{K} = \mathbb{Z}_2^{2n}$ :

$Q \leq \frac{2 lm 2^n}{2^{2n}} = \frac{2lm}{2^n}.$

что и требовалось доказать.

Определение
Пусть $\sigma$ — подстановка из $S_{\left\vert\,\mathcal{P}\,\right\vert}$ , а $K = \left\langle K_1, K_2 \right\rangle$ — некоторый ключ.
Будем говорить, что пара $\left\langle \sigma, K \right\rangle$ удовлетворяет (satisfies) множествам $E$ –пар $\mathsf{E}$ и $P$ –пар $\mathsf{P}$ , если выполняются следующие условия:

подстановка $\sigma$ неотличима от истинной подстановки $\pi$ на полученных множестве $P$ –пар:

$\forall \left\langle M, \pi(M) \right\rangle \in \mathsf{P} \>\Longrightarrow\> \sigma(M) = \pi(m),$

подстановка $\sigma$ неотличима от истинной подстановки $\pi$ на полученных множестве $E$ –пар: