[Из песочницы] Метод фрактального многообразия в задачах Data Science04.05.2018 15:03

1. Постановка задачи

Наборы числовых упорядоченных данных можно разделить на две группы: гауссовы и странные (негауссовы). Если к гауссовым данным можно применять количественное сравнение, то к странным данным такой подход неприменим ввиду их относительности и отсутствия стандарта, что оставляет возможным лишь качественный анализ, который во многих случаях является неоднозначным и трудоемким. При этом такие данные широко распространены, а задача их анализа является актуальной для многих областей науки.

Далее будет представлен вычислительный метод, преобразующий исходные негауссовы данные в гауссовы, что позволяет в дальнейшем сравнивать количественно структурные характеристики больших наборов данных.

Преобразованное значение негауссовых данных, допускающее количественное сравнение, должно быть инвариантно относительно любых линейных преобразований значений исходных данных, нечисловая статистика [1]. Задача имеет решение только для упорядоченных странных данных и с учётом окрестности, в которой проявляется нелинейность.

2. Вычислительный метод

Преобразованное значение негауссовых данных, допускающее количественное сравнение, должно быть инвариантно относительно любых линейных преобразований значений исходных данных [1]. Задача имеет решение только для упорядоченных странных данных и с учётом окрестности, в которой проявляется нелинейность. Как показано в работе, преобразование должно обладать ренормгрупповой инвариантностью в отношении размера окрестности, в которой происходит количественное сравнение проявлений нелинейности.

Далее приводятся ключевые шаги вывода формулы отношения сигнала к шуму, допускающего количественное сравнение. Фрактал пыль Кантора или геометрическая прогрессия с произвольным значением 0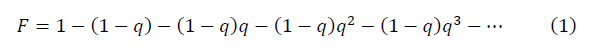
Предлагается следующий способ построения фрактального многообразия. Фрактальное многообразие для n=5 произвольного набора пяти упорядоченных чисел 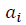имеет вид: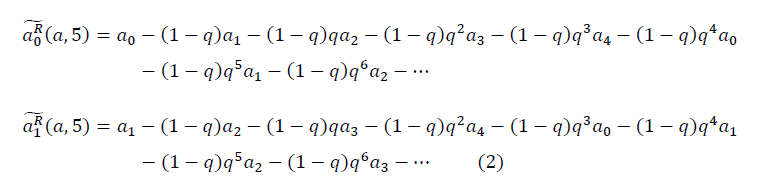

С каждым фрактальным циклом m, где m→∞, появляется новое число 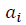из выборки негауссовых данных n и далее по замкнутому контуру. Различается левое и правое направление обхода контура. В общем виде: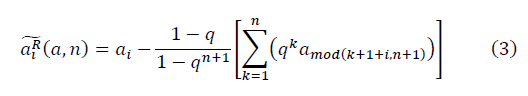

Аналогично для 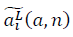 получается: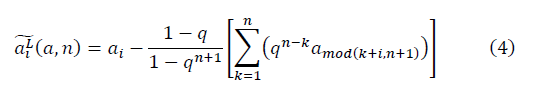

Здесь и далее формулы в обозначении Mathcad.

Множества 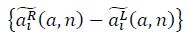и 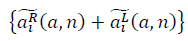 образуют фрактальные многообразия. Определяется выражение для отношения сигнала к шуму: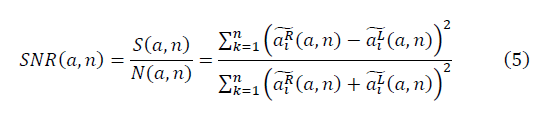

Уникальность функций Гаусса, Бесселя состоит в том, что отношение сигнала к шуму SNR в определении (5) не зависит от значения n. При аппроксимации данных функциями Бесселя коллективный эффект не проявляется.

При моделировании негауссовых данных полуволной 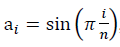, что применяется в расчётах с предварительной аппроксимацией данных конечным рядом Фурье, для достаточно больших значений n выражение отношения сигнала к шуму имеет вид: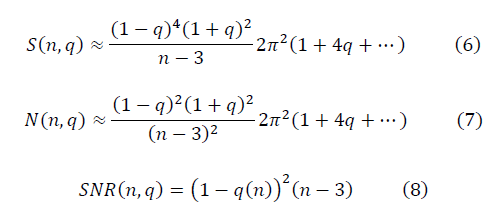

Потребуем выполнение условия ренормгрупповой инвариантности SNR (n, q), приближающее странные данные к гауссовым: при изменении n→n' происходит преобразование q→q', оставляющее значение SNR (n, q) (8) неизменным в методе ренормализационной группы [2]. Требование ренормгрупповой инвариантности выполняется при условии: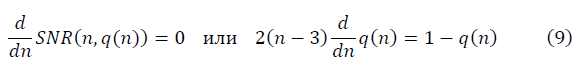

Решение дифференциального уравнения имеет вид: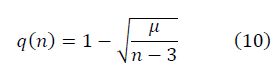

Выбор постоянной величины μ задаёт масштаб отношения сигнала к шуму.

Для больших значений n, асимптотики параметров длины фрактальных многообрази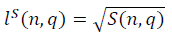й и 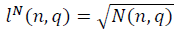 в модели полуволны 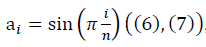, с учётом ренормгруппового уравнения для q (n) (10) имеют вид: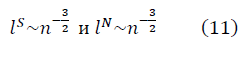

Хаусдорфова фрактальная размерность по Колмогорову [3] для фрактальных многообразий, построенных с учётом направления обхода замкнутого контура из n чисел: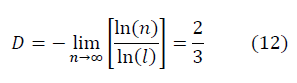

Среднее как для гауссовых чисел: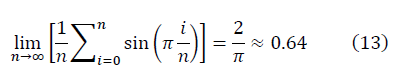

отличается от среднего по Колмогорову для D=2/3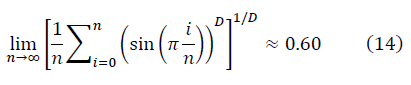

В качестве иллюстрации метода фрактального многообразия приводятся вычисления для биномиальных коэффициентов, близких к гауссову множеству, нормированных на асимптотику: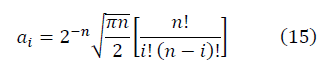

Для достаточно больших значений n выражение отношения сигнала к шуму имеет вид: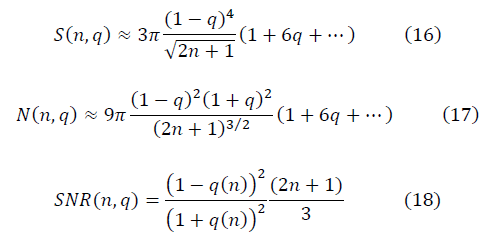

Ренормгрупповое уравнение для q (n):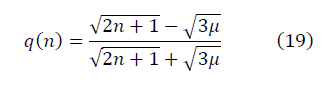

Фрактальная размерность для нормированных биномиальных коэффициентов D=4/5.

Выбор среднего для негауссовых данных как для гауссовых чисел часто применяемый в расчётах, не является однозначным [1]. Не только само значение среднего, но и вид формулы для вычисления среднего значения определяется странными данными. Метод фрактального многообразия позволяет точнее определить такую известную характеристику структуры как среднее значение, используя в качестве инструмента более мелкий масштаб 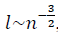, по сравнению с евклидовым масштабом 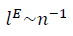и выявить качественно новую структурную характеристику — степень взаимной корреляции данных или степень коллективного состояния данных, определяемой SNR.

Таким образом, появление зависимости SNR от числа выборки n для негауссовых данных объясняется наличием взаимной корреляцией негауссовых данных. Внедрение параметра q фрактала пыль Кантора и применение метода ренормгрупповой инвариантности в отношении SNR позволяет перейти к традиционному анализу гауссовых данных — степени корреляции данных в определении SNR (5).

Проводятся предварительные вычисления при q=0 по формулам (24)-(26). На предварительном этапе расчётов, при сравнении различных наборов упорядоченных данных, получаются критические размеры дескрипторов n (кр1), n (кр2) обеспечивающие максимальные коллективные состояния в наборах данных. Тогда принимается значение 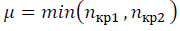-3 в формуле (10) и уточняется значение 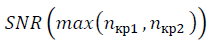с учётом ренормгрупповой инвариантности (20)-(23). Сравнение значений SNR разных наборов данных является корректным при вычислении, выполненном в одном масштабе μ. Пиковые значения 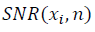характеризуют наличие структуры в данных переменной x, обозначают окрестность коллективного состояния. Понятие критического или коллективного состояния характерно в подходе странной кинетики, обозначая кластер степеней свободы с сильной корреляцией. Поведение системы в окрестности коллективного состояния носит универсальный характер и не зависит от природы взаимодействия, вызывающего корреляцию [5], как и универсальность распределения случайных величин в отсутствии взаимной корреляции.

Параметры аппроксимации конечного ряда Фурье и размер дескриптора n при прохождении упорядоченных данных с единичным шагом определяются из условия максимума целевой функции — максимального коллективного состояния в системе.

В матричном виде ренорм-инвариантные формулы для отношения сигнала к шуму имеют вид: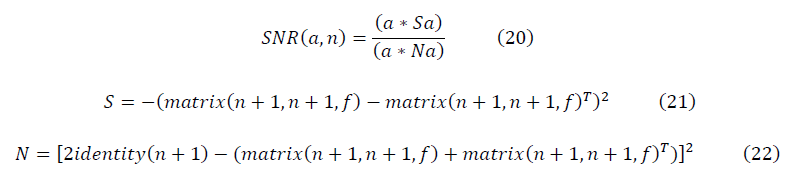

где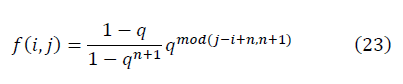

Результаты вычислений по формулам (11)-(14) эквивалентны результатам исходных вычислений по формулам (3)-(5), при этом позволяют составление алгоритма.
В расчётах из K=n/2+1 уникальных упорядоченных данных спектра строится симметричный вектор: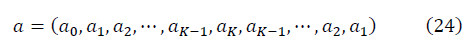

Для достаточно больших K, когда выполняется условие ренормгрупповой инвариантности, и q=0, с учётом симметрии матриц S и N, формулы для отношения сигнала к шуму приобретают вид: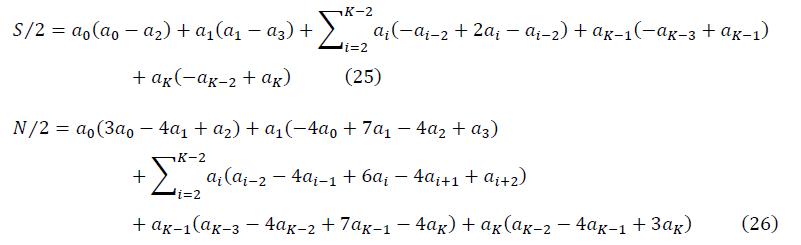

При сопоставлении значений SNR со шкалой упорядочивания, шкала сдвигается влево на размер дескриптора K. Упорядоченный набор данных, с предварительной аппроксимацией конечным рядом Фурье k, проходят дескриптором, размером K, с единичным шагом. Вычисляется 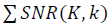по проходу всех точек в наборе данных. Целевая функция определяется как  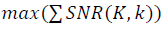при переборе параметров K и k. Как уже отмечалось, корректное сравнение структурных характеристик SNR разных наборов данных должно осуществляться в едином масштабе μ с учётом ренормгрупповой инвариантности ((20)-(23)). Подобно сравнению измерений, выполненных в сантиметрах и дюймах.

Вычислительный метод применяется для больших наборов данных, полученных в хорошем разрешении, что позволяет увеличить масштаб сравнения μ с сохранением ренормгрупповой инвариантности. По порядку величин, в задаче с конформерами общее число данных в спектре рентгеноструктурного анализа — 2250 значений, оптимальный размер дескриптора для данного разрешения K=585, максимальная гармоника конечного ряда Фурье k=3.

3. Выводы

Метод применим в определении областей с сильной корреляцией степеней свободы между собой и количественном сравнении степени корреляции больших наборов упорядоченных данных. Например, когда неприменимо приближение Хартри-Фока. Интерпретация результатов обработки данных основана на построении фрактального многообразия, которое моделирует коллективное или критическое состояние [4] в одномерном пространстве. Интерпретацию усложняет неоднозначность терминологии, описывающей коллективное состояние в разных задачах.

Коллективным состоянием в химии называют гибкость или подвижность молекулярных фрагментов. Гипотеза Кошланда индуцированного соответствия при проявлении биологической активности, основанная на допущении гибкости активного центра фермента, удовлетворительно объясняет действие ферментов. При приближении субстрата к активному центру фермента, в молекуле фермента синхронно происходит конформационная перестройка, затрагивающая большое число степеней свободы. Применение вычислительного метода к спектру трёх конформеров показывает значительное увеличение коллективного эффекта у конформера, отличающегося биологической активностью. Аналогичный, с проявлением биологической активности, пример коллективного эффекта проявляется в методе термомеханической кривой для полимеров с разной молекулярной массой в области высокой эластичности.

Применение универсальной формулы преобразования к большим наборам негауссовых данным с учётом свойств инвариантности относительно любых линейных преобразований и ренормгрупповой инвариантности, делает возможным количественное сравнение коллективных состояний. Метод применяется при решении задач data science в предварительном преобразовании исходных негауссовых данных и сравнении степени взаимной корреляции данных и в поиске количественных соотношений структура — свойство.

4. Литература

1. Орлов А.И. Прикладная статистика. — М.: Экзамен, 2006. — 574 с
2. Боголюбов Н. Н., Ширков Д.В. Введение в теорию квантованных полей. — 4-е изд., испр. — М.: Наука Главной редакции физико-математической литературы, 1984. — 600 с.
3. Колмогоров А.Н., Новый метрический инвариант транзитивных динамических систем и автоморфизмов пространств Лебега, — 1958, Доклады АН СССР, №5, С. 861 — 864
4. Зелёный Л.М., Милованов А.В. Успехи физических наук, Фрактальная топология и странная кинетика: от теории перколяции к проблемам космической электродинамики, — 2004, №8, С. 809 — 852

© Habrahabr.ru