[Из песочницы] Космос как база данных
В статье приводится метод построения проекции галактической орбиты Солнечной системы через анализ пространственного перепада космологического красного смещения. Кроме известных движений вращения вокруг центра Галактики и смещения вверх-вниз относительно её диска, на результатах ясно просматривается «покачивание» оси.

Рис. 0. Визуальное представление минимумов (зелёный) перепада красного смещения на воображаемой гелиоцентрической сфере — результат вращения Солнечной системы вокруг центра Млечного Пути. Чёрная ось — X (положительные направо), красная полупрозрачная — Y (положительные вглубь), синяя — Z (положительные наверх). Жёлтый шар — направление движения согласно жёлтой тенденции (RA 10, DEC -30) — движение Солнечной системы под диск Млечного Пути. Чёрный шар — актуальное направление на Стрельца-А (RA 266, DEC -29), центр Млечного Пути.
Введение
Мне всегда было интересно, что же было в самом начале — снять завесу с тайны творения. Наверное, раньше такие люди становились археологами, и копали землю, песок, глину. Теперь всё изменилось, и копать приходится данные.
Не так давно я наткнулся на результаты работы группы Сола Перлмуттера, за которую он, Брайан Шмидт и Адам Рисс получили Нобелевскую премию по физике за 2011-ый год. Вы, вероятно, об этом слышали, если интересуетесь космологией.

Рис. 1. График зависимости красного смещения (ось абсцисс) и конформного расстояния (ось ординат) для объектов типа сверхновая типа Ia.
Сверхновая достаточно редкое явление, тем более конкретного типа Ia, поэтому в представленной в работе выборке всего 582 позиции.
Уникальность данного явления для исследования космоса в том, что оно протекает в течение известного промежутка времени, с известной кривой изменения светимости. Это с одной стороны. С другой — в гигантских расстояниях, с которых его можно зафиксировать и исследовать.
Таким образом, сверхновые типа Ia выступают своего рода калибратором лестницы расстояний, с помощью которого она может быть значительно увеличена.
Скажу проще, исследование Перлмуттера сопоставило значения космологического красного смещения (далее ККС) с расстояниями, в результате чего был обнаружен не пропорциональный рост ККС, с вытекающим в рамках стандартной космологической модели выводом об ускоренном расширении Вселенной.
Вот здесь хорошо и понятно написано про становление современной космологической модели.
В исследовании Перлмуттера было не много данных, но хороших — с достоверными расстояниями. Я подумал, почему бы, вопреки советам Сенеки, не поискать бриллиант в навозе: порыться в «плохих» данных, где ККС одних источников можно сопоставлять лишь с ККС других источников с учётом их пространственной ориентации.
Тем более что такого «навоза» в разы больше, а инструменты автоматизированы. Многие годы астрономы всего мира собирали по крупицам данные о всевозможных космических объектах, делили их на виды и классы, рассчитывали гелиоцентрические положения, измеряли светимости, красные смещения и прочее.
База ZCAT состоит из данных о 929 094 космических объектах.
Из них мы будем пользоваться данными только о 895 441 объектах — с известным ККС, измеренным в условно одной точке (по космическим масштабам наше смещение за интервалы измерений ничтожно). Для части из них — 563 объекта — известно даже расстояние, вычисленное не связанными с ККС методами.
Инструментарий
Информация об использованных программных продуктах.
Система управления базами данных: Microsoft SQL Server Management Studio 10.0.1600.22 ((SQL_PreRelease).080709–1414) Компоненты доступа к данным (MDAC) 10.0.16299.15 (WinBuild.160101.0800)
Microsoft MSXML 3.0 4.0 5.0 6.0
Microsoft Internet Explorer 9.11.16299.0
Microsoft .NET Framework 2.0.50727.8838
Операционная система 6.3.16299
MS Office ver.10.
Описание БД
У каждого элемента в БД множество полей, из которых нас будут интересовать только его положение на небосводе во второй экваториальной системе координат и его ККС, которое в большинстве случаев было приведено как скорость, и пересчитано в соответствии с источником (по формуле v=zc).
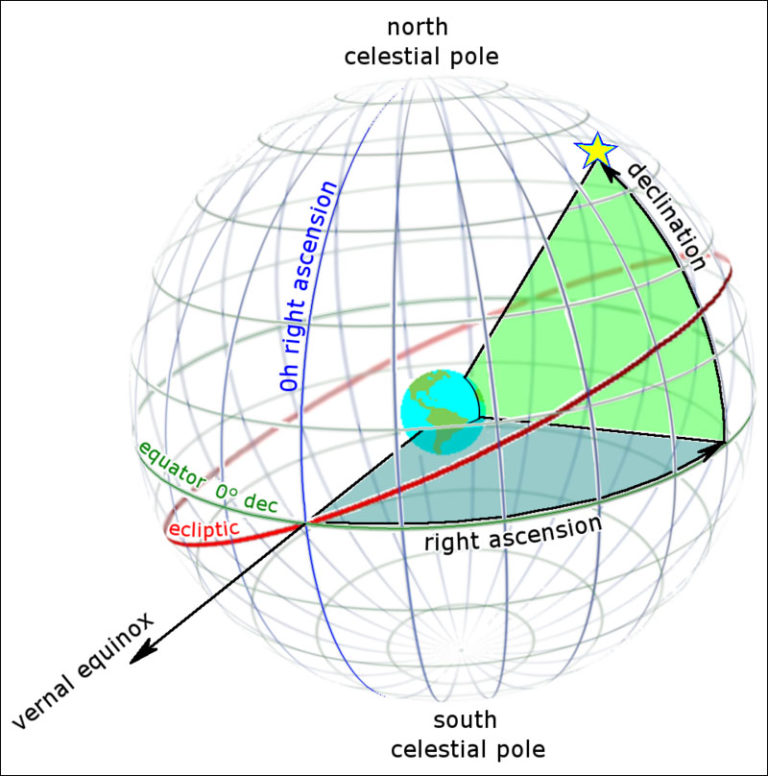
Рис. 2. Вторая экваториальная система координат. Прямое восхождение (right ascension) откладывается по экватору от точки весеннего равноденствия (vernal equinox). Наклонение (declination) — к полюсам (положительное наклонение — к северному, отрицательное — к южному).
Пара замечаний. В базе дынных приведены гелиоцентрические значения, следовательно, в центре рисунка 2 стоит представить Солнце.
Также в БД приведены значения относительно Солнечной системы, без учёта вращения последней вокруг Стрельца-А. Это будет хорошо видно по результатам.
Вообще, меня завораживает наблюдать, пусть даже на графиках и диаграммах, процессы, происходившие миллиарды лет назад. Удивительно, как по характеристикам долетающих до нас фотонов можно восстанавливать картины глубокого прошлого. Пусть даже эти картины по качеству далеки от красивых, цветных фотографий, к которым мы теперь привыкли.
Столбцы исходной базы:
RA_HR — прямое восхождение (часы)
RA_MIN — прямое восхождение (минуты)
RA_SEC — не используется
DEC_Sign — наклонение (знак)
DEC_DEG — наклонение (градусы)
DEC_MIN — наклонение (минуты)
DEC_SEC — не используется
Z — величина ККС, z.
Рассчитанные значения:
Xd, Yd, Zd — рассчитанная величина проекции единичного вектора по лучу направления (d от direction, destination) элемента на оси x, y, z, соответственно.
Метод половин
Если разделить пространство на два полушария любой плоскостью, проходящей через Солнце, то мы получим два множества элементов A и B, в каждом из которых окажется некоторое количество элементов [QuantityA] и [QuantityB] с некоторым суммарным ККС [RSh_SumA] и [RSh_SumB], а в результате — средним количеством ККС на элемент [RSh_midA] и [RSh_midB], и их разностью [RSh_dif].
Для удобства неплохо было бы зафиксировать систему координат.
Осью X будет прямая, содержащая начало координат (Солнце) и точку с прямым восхождением 0 часов 0 минут и наклонением 0 градусов, то есть совпадающая с направлением на точку весеннего равноденствия. Ось Y будет также лежать в плоскости экватора — прямое восхождение 9 часов 0 минут 0 секунд, наклонение 0 градусов. Ось z — наклонение 90 градусов, прямое восхождение любое.
Также определим три опорных плоскости. Удобно это сделать перпендикулярными прямыми:
плоскость α перпендикулярна z, содержит x и y;
плоскость β перпендикулярна y, содержит x и z;
плоскость γ перпендикулярна x, содержит y и z.
И посмотрим на разность среднего смещения для этих плоскостей:
α = 0,07491884 = 22 460,1 км/сек
β = 0,012127832 = 3 635,8 км/сек
γ = -0,034180049 = -10 246,9 км/сек
Я акцентирую внимание читателя на величинах среднего отклонения ККС на каждый объект: каждый космический объект в северном полушарии (здесь и далее речь о второй экваториальной системе координат относительно Солнца), либо верхнем полупространстве, примерно на 0,075 сдвинут по спектру к красному, чем каждый объект в южном полушарии.
Как если бы мы двигались относительно него, удаляясь, со скоростью примерно 11 230 км/с (делим значение перепада относительно α = 22 460,1 км/с на два). Деление на два здесь обусловлено тем, что мы брали значения красного смещения относительно противоположной стороны пространства, к объектам которого получили бы смещение в фиолетовую сторону, равное по величине красному смещению, что обусловило бы двукратную разность смещений по направлениям.
Но такая разность среднего значения «по сторонам света» очень велика в сопоставлении с известными пекулярными скоростями Солнечной системы и Млечного пути, максимальная из которых — относительно реликта — достигает только 627±22 км/с.
Здесь хорошо разложено.
В начале, я предполагал, что основная причина такого перепада кроется в отсутствии выделения масштабной составляющей красного смещения в соответствии с метрикой Фридмана-Робертсона-Уокера.
То есть, по причине того, что по мере удаления от источника красное смещение возрастает нелинейно по времени, оно содержит в себе немалую составляющую от расширения Вселенной, и пекулярная скорость точки приёма относительно «старых пластов» излучения выражена «ярче».
Однако, пекулярная скорость точки приёма относительно излучения любой давности даст одинаковый, не масштабированный результат.
Основная причина перепада кроется в повторяющихся и сонаправленных движениях (вращении) вокруг центра Млечного Пути, которые происходили в масштабе своей эпохи, и потому, вносят теперь огромный вклад в фиксируемый перепад, вместе с тем предоставляя нам потенциальную возможность отделить зёрна от плевел. А также, вероятно, в наличии ещё более длительных направленных движений.
Об этом далее в главе «Эффект памяти КС», а пока копнём глубже, вновь обратившись к данным. Каким образом мы могли бы улучшить понимание физических явлений?
Во-первых, приведённые данные по плоскостям могут составлять проекции некоего вектора движения, который в абсолютном значении должен получиться больше приведённых значений. То есть, если мы хотим проверить предположение о наличии такого движения (например, в рамках явлений тёмного потока или великого аттрактора), стоит повращать делящей плоскостью в поисках максимальных значений.
Во-вторых, мы можем выполнять действие из пункта один — вращение плоскостью, постепенно уменьшая выборку объектов с каждой стороны, ограничивая её за счёт исключения элементов находящихся в тороидальной области вокруг вектора, задающего делящую плоскость. Как если бы мы сужали луч прожектора в каждую сторону от делящей плоскости.
Если перепад красного смещения обусловлен движением точки наблюдения относительно сторон космического пространства, то такое сужение должно последовательно увеличивать среднее значение красного смещения, за счёт того, что исключаемые объекты обладают меньшим вкладом в красное смещение такой природы.
В-третьих, при вращении делящей плоскости мы можем брать в расчёт только часть диапазона ККС, чтобы постараться проследить, как изменялись максимумы и их направления. И совместить это с приёмом из второго пункта.
Вращение делящей плоскости
Это лишь проверка некоторых предположений, потому я облегчил работу своему ноутбуку, сократив один проход по времени до 15–20 минут следующим образом: исключены угловые секунды объектов (их вклад в значения ничтожен); плоскость вращается с шагом в 5°.
Механизм вращения таков: значение прямого восхождения проходит значения от 0° до 360° с шагом 5° для каждого значения наклонения от 0° до 90° с шагом 5°.
Таким образом, мы проходим полусферу под всеми возможными углами. Вторую полусферу проходить нет смысла — она полностью зеркальна с обратным знаком (как, например, и первый проход прямого восхождения для наклонения 0°).
create table [RedShiftResearch].[dbo].[RShField6](
[QNum1] [int] NULL,
[QNum2] [int] NULL,
[RA_surface_ort_angle] [float] NULL,
[DEC_surface_ort_angle] [float] NULL,
[X_ort] [float] NULL,
[Y_ort] [float] NULL,
[Z_ort] [float] NULL,
[Ort_sum] [float] NULL,
[QuantityA] [int] NULL,
[QuantityB] [int] NULL,
[CheckQSum] [int] NULL,
[RSh_sumA] [float] NULL,
[RSh_sumB] [float] NULL,
[RSh_sumCheck] [float] NULL,
[RSh_midA] [float] NULL,
[RSh_midB] [float] NULL,
[RSh_dif] [float] NULL)
DECLARE @DIAPASON_L float = -3;
DECLARE @DIAPASON_H float = 20;
DECLARE @counter1 int = 0;
DECLARE @counter2 int = 0;
DECLARE @Q1 int;
DECLARE @Q2 int;
DECLARE @RA_surf_ort_angle float;
DECLARE @DEC_surf_ort_angle float;
DECLARE @X_ort float;
DECLARE @Y_ort float;
DECLARE @Z_ort float;
DECLARE @X_ort_neg float;
DECLARE @Y_ort_neg float;
DECLARE @Z_ort_neg float;
DECLARE @Ort_sum float;
DECLARE @RA_surf_step float = 5.0;
DECLARE @DEC_surf_step float = 5.0;
DECLARE @QuantityA int;
DECLARE @QuantityB int;
DECLARE @CheckQSum int;
DECLARE @RSh_sumA float;
DECLARE @RSh_sumB float;
DECLARE @RSh_sumCheck float;
DECLARE @RSh_midA float;
DECLARE @RSh_midB float;
DECLARE @RSh_dif float;
DECLARE @threshold float = 2.0;
WHILE (@counter1 < 19)
begin
WHILE (@counter2 < 72)
begin
SET @Q1 = @counter1;
SET @Q2 = @counter2;
SET @RA_surf_ort_angle = @counter2 * @RA_surf_step;
SET @DEC_surf_ort_angle = @counter1 * @DEC_surf_step;
SET @Z_ort = SIN(@DEC_surf_ort_angle/180.0*PI());
SET @X_ort = ROUND(COS(@RA_surf_ort_angle/180.0*PI())*COS(ASIN(@Z_ort)),15);
SET @Y_ort = ROUND(SIN(@RA_surf_ort_angle/180.0*PI())*COS(ASIN(@Z_ort)),15);
SET @X_ort_neg = -1 * @X_ort;
SET @Y_ort_neg = -1 * @Y_ort;
SET @Z_ort_neg = -1 * @Z_ort;
SET @Ort_sum = @X_ort*@X_ort+@Y_ort*@Y_ort+@Z_ort*@Z_ort;
SELECT @QuantityA = COUNT(*) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE([Xd]+@X_ort)+SQUARE([Yd]+@Y_ort)+SQUARE([Zd]+@Z_ort))>@threshold);
SELECT @QuantityB = COUNT(*) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE([Xd]+@X_ort_neg)+SQUARE([Yd]+@Y_ort_neg)+SQUARE([Zd]+@Z_ort_neg))>@threshold);
SET @CheckQSum = @QuantityA+@QuantityB;
SELECT @RSh_sumA = SUM([Z]) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE([Xd]+@X_ort)+SQUARE([Yd]+@Y_ort)+SQUARE([Zd]+@Z_ort))>@threshold);
SELECT @RSh_sumB = SUM([Z]) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE([Xd]+@X_ort_neg)+SQUARE([Yd]+@Y_ort_neg)+SQUARE([Zd]+@Z_ort_neg))>@threshold);
SET @RSh_sumCheck = @RSh_sumA+@RSh_sumB;
SET @RSh_midA = @RSh_sumA / @QuantityA;
SET @RSh_midB = @RSh_sumB / @QuantityB;
SET @RSh_dif = @RSh_midA - @RSh_midB;
insert into RShField6(QNum1, QNum2, RA_surface_ort_angle, DEC_surface_ort_angle, X_ort, Y_ort, Z_ort, Ort_sum, QuantityA, QuantityB, CheckQSum, RSh_sumA, RSh_sumB, RSh_sumCheck, RSh_midA, RSh_midB, RSh_dif)
values (@counter1,
@counter2,
@RA_surf_ort_angle,
@DEC_surf_ort_angle,
@X_ort,
@Y_ort,
@Z_ort,
@Ort_sum,
@QuantityA,
@QuantityB,
@CheckQSum,
@RSh_sumA,
@RSh_sumB,
@RSh_sumCheck,
@RSh_midA,
@RSh_midB,
@RSh_dif
);
set @counter2 = @counter2+1;
end
set @counter1 = @counter1+1;
set @counter2 = 0;
end
select *
from [dbo].[RShField6];
На выходе для полного диапазона красного смещения получаем таблицу, сопоставляющую значение перепада с направлением вектора, задающего делящую плоскость. После чего уже в MS Excel она приводится к виду, позволяющему визуализировать данные, как представлено на диаграмме ниже.
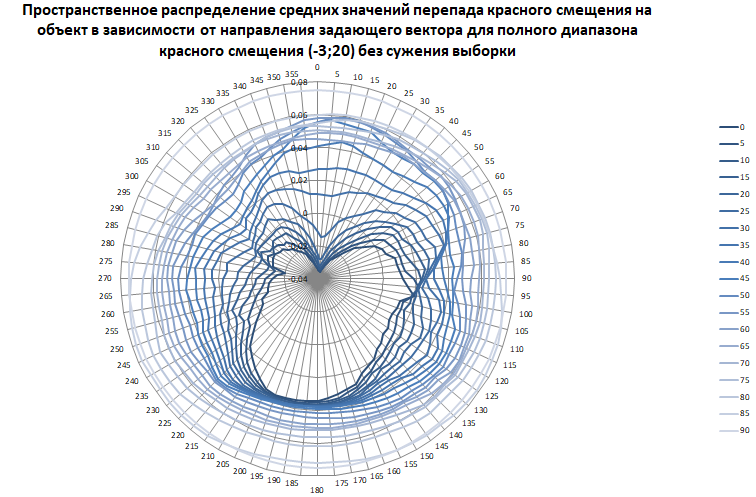
Рис. 3. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати без сужения выборки.
Абсолютный минимум: минус 0,03535 при 0° наклонении 10° (40 минут) прямого восхождения.
Абсолютный максимум: 0,078 при 85° наклонении 125° (8 часов 20 минут) прямого восхождения.
Всего в выборке для максимума 895439 объектов.
На рисунке 3 показано как изменяется среднее значение по мере изменения направления.
Одна замкнутая кривая — проход на 360° при неизменном наклонении. Чем темнее цвет кривой, тем ближе она к экватору, и наоборот, чем светлее — тем ближе к северному полюсу.
Удобная интерпретация диаграммы такова: мы как бы смотрим на Солнечную систему с южного полюса координат; лучи, приходящие по экватору на воображаемую сферу с центром — Солнцем, формируют более тёмные линии, чем блекнущие по мере удаления к северному полюсу сферы лучи.
Диаграмма для южного полушария будет являться зеркальной диаграммой северного полушария с обратным знаком.
Максимум, действительно, оказался больше, чем любое из ранее приведённых значений для опорных плоскостей α, β и γ, и сонаправлен с α. Однако он не является векторной суммой их значений, потому что значения α и γ, как видно из диаграммы, являются результатами разных процессов. Всего таких тенденций три. Я отмечу две из них зелёным и жёлтым цветом на следующем рисунке.
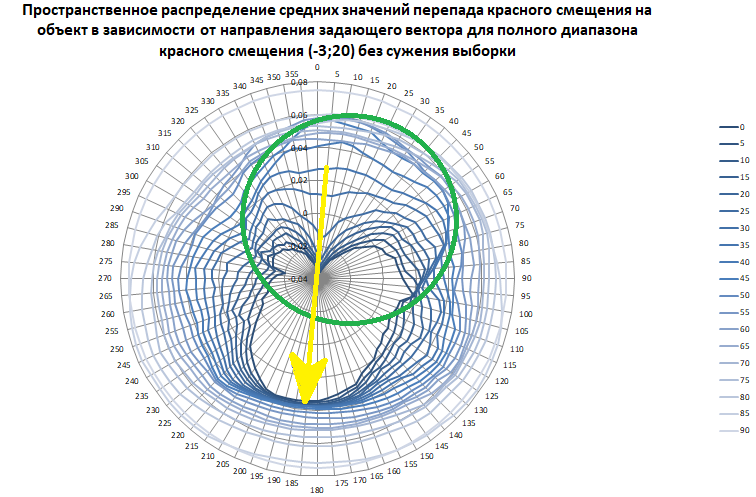
Рис. 4. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати без сужения выборки. С обозначением тенденций зелёным и жёлтым цветом.
Не изображённой тенденцией остаётся красная. Она словно шапка надета на диаграмму и форму двух других тенденций. Это увеличение среднего перепада КС с увеличением наклонения.
Большая красная стрелка указывает с южного полюса через Солнце на северный. Ну, почти. Максимум — наклонение 85° прямое восхождение 125° (8 часов 20 минут).
Снова же отставим анализ, продолжим путешествие по данным.
Изменение характера выборки
Тем, кто читал пример запроса, будет понятнее, но постараюсь максимально развёрнуто.
SELECT @QuantityA = COUNT (*) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE ([Xd]+@X_ort)+SQUARE ([Yd]+@Y_ort)+SQUARE ([Zd]+@Z_ort))>@threshold);
SELECT @QuantityB = COUNT (*) FROM dbo.RSh8 where ([Z]>@DIAPASON_L) AND ([Z]<@DIAPASON_H) AND ([Z]<>0) AND ((SQUARE ([Xd]+@X_ort_neg)+SQUARE ([Yd]+@Y_ort_neg)+SQUARE ([Zd]+@Z_ort_neg))>@threshold);
Условием соответствия множеству A или B в программе запроса принято соответствие длины векторной суммы орта расположения объекта и орта, перпендикулярного делящей плоскости, требованию >@threshold (порог).
Проще говоря, если направление на объект находится с той же стороны опорной плоскости, например α, что и задающий её орт x, направленный на точку весеннего равноденствия, то длина их векторной суммы должна быть больше корня из двух.
С корнем работать неудобно, поэтому оставим просто два и левую часть уравнения тоже оставим в квадрате, как в примере выше. Это порог для множества объектов A.
SET @X_ort_neg = -1 * @X_ort;
SET @Y_ort_neg = -1 * @Y_ort;
SET @Z_ort_neg = -1 * @Z_ort;
Для наглядности приведу условия двух выборок в плоскости на рисунках 5 и 6.
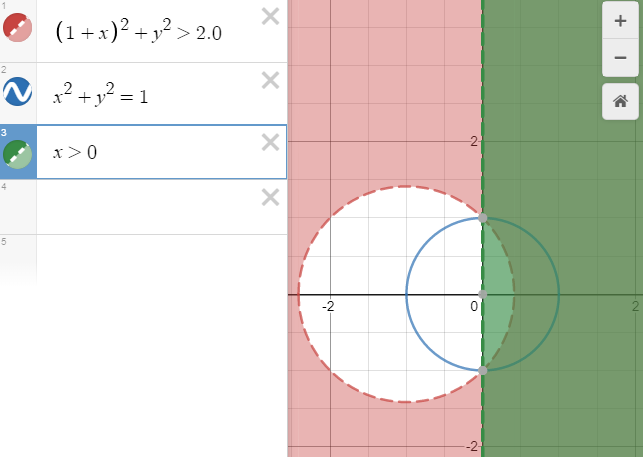
Рис. 5. Первое условие: суммой крайнего вектора направления (0;1) и орта (1;0) будет вектор длиной SQRT (2)
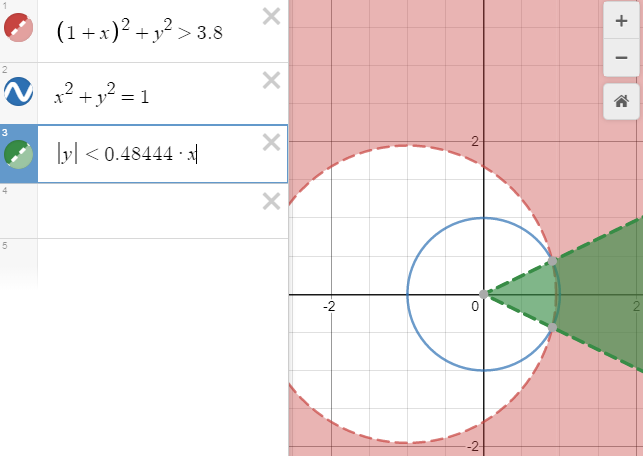
Рис. 6. Первое условие: суммой крайнего вектора направления и орта (1;0) будет вектор длиной SQRT (3.8). Второе условие: координаты орта направления всегда являются катетами треугольника с гипотенузой равной единице. В итоге (зелёным), в выборку попадут все точки, направление на которые совпадает с ортом, задающим плоскость, и откланяется от него не более, чем до точки пересечения двух предыдущих условий. То есть не более, чем на угол ≈25.8°, для коэффициента сужения 3.8.
Если для обоих случаев на рисунках 5 и 6 провернуть область вокруг оси абсцисс на 180°, то получится пространственное ограничение выборки в виде бездонного конуса для рисунка 6, и его вырожденного варианта — полупространства — для рисунка 5.
Для противоположной выборки условие зеркально — симметрично относительно оси ординат.
То есть, если мы начинаем увеличивать коэффициент сужения, то в выборку перестают попадать объекты, находящиеся в тороидальной обрасти вокруг оси задающих векторов, симметричной относительно делящей плоскости.
Теперь проверим как ведут себя установленные зелёная, жёлтая и красная тенденции с сужением выборки указанным выше способом.
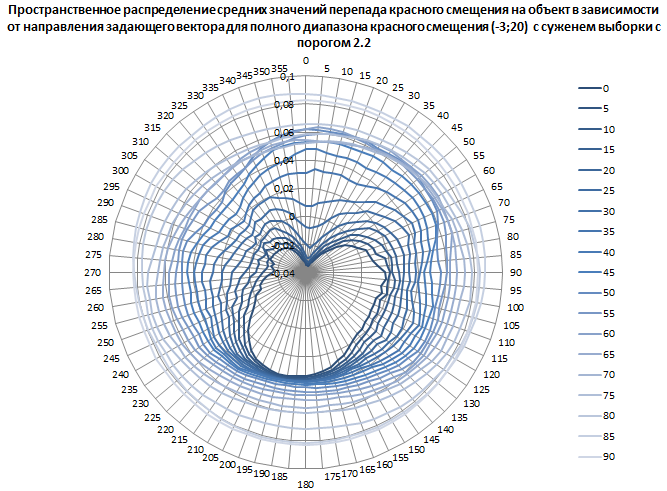
Рис. 7. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 2.2.
Абсолютный минимум: минус 0,035112483 при 0° наклонении 15° (1 час) прямого восхождения.
Абсолютный максимум: 0,088327442 при 85° наклонении 340° (22 часа 40 минут) прямого восхождения.
В выборке для максимума 662 761 объектов.
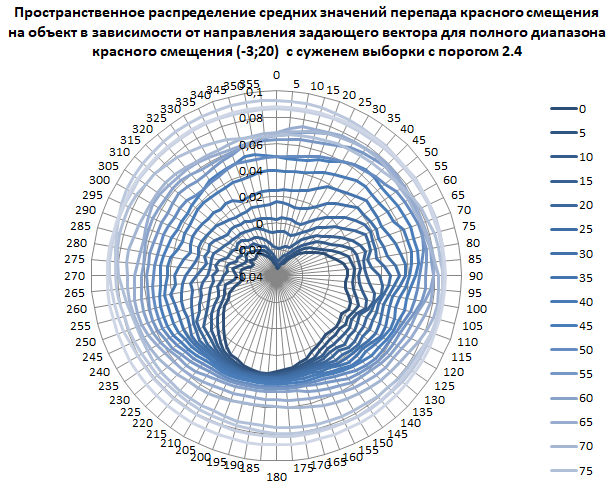
Рис. 8. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 2.4.
Абсолютный минимум: минус 0,034270309 при 0° наклонении 5° (20 минут) прямого восхождения.
Абсолютный максимум: 0,085673496 при 90° наклонении.
Всего в выборке для максимума 572 258 объектов.

Рис. 9. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 2.6.
Абсолютный минимум: минус 0,030690323 при 0° наклонении 5° (20 минут) прямого восхождения.
Абсолютный максимум: 0,085673496 при 85° наклонении 140° (9 часов 20 минут) прямого восхождения.
Всего в выборке для максимума 527 397 объектов.
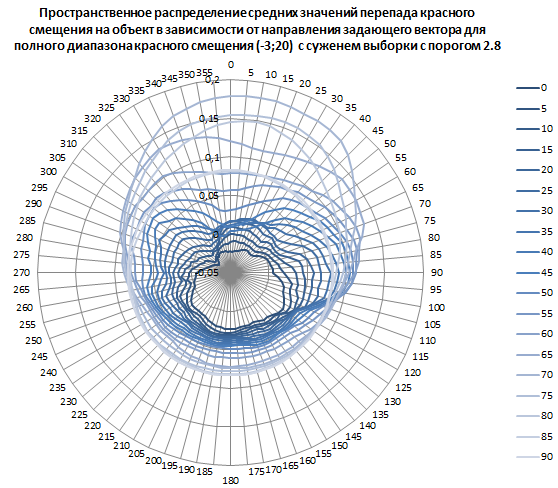
Рис. 10. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 2.8.
Абсолютный минимум: минус 0,0328635 при 0° наклонении 305° (20 часов 20 минут) прямого восхождения.
Абсолютный максимум: 0,180024201 при 70° наклонении 10° (40 минут) прямого восхождения.
Всего в выборке для максимума 341 945 объектов.
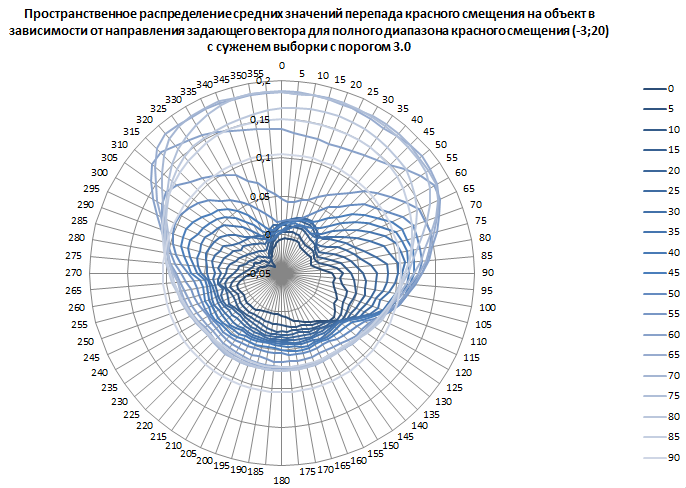
Рис. 11. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 3.0.
Абсолютный минимум: минус 0,037789532 при 0° наклонении 310° (20 часов 40 минут) прямого восхождения.
Абсолютный максимум: 0,187621081 при 70° наклонении 340° (22 часа 20 минут) прямого восхождения. Всего в выборке для максимума 260 398 объектов.
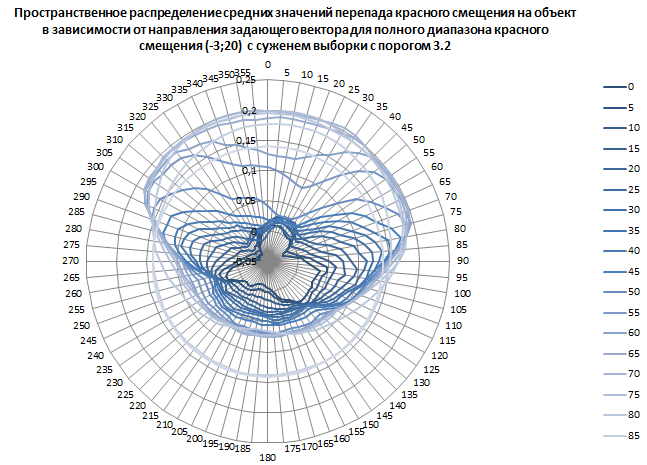
Рис. 12. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 3.2.
Абсолютный минимум: минус 0,037522009 при 0° наклонении 280° (18 часов 40 минут) прямого восхождения.
Абсолютный максимум: 0,204479206 при 70° наклонении 30° (2 часа 0 минут) прямого восхождения. Всего в выборке для максимума 156 482 объектов.
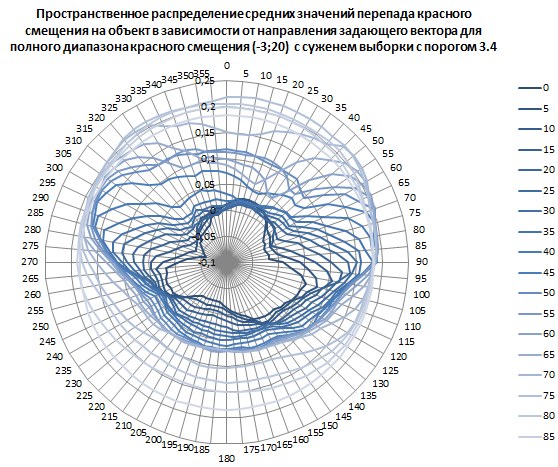
Рис. 13. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 3.4.
Абсолютный минимум: минус 0,058609459 при 0° наклонении 285° (19 часов 0 минут) прямого восхождения.
Абсолютный максимум: 0,221096202 при 75° наклонении 15° (1 час 0 минут) прямого восхождения. Всего в выборке для максимума 92 908 объектов.

Рис. 14. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 3.6.
Абсолютный минимум: минус 0,084653998 при 0° наклонении 290° (19 часов 20 минут) прямого восхождения.
Абсолютный максимум: 0,2319195 при 85° наклонении 25° (1 час 40 минут) прямого восхождения. Всего в выборке для максимума 72 887 объектов.
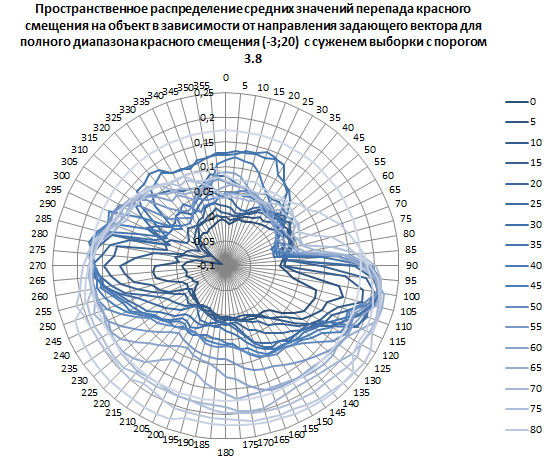
Рис. 15. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для полного диапазона красного смещения от минус трёх до двадцати с сужением выборки с порогом 3.8.
Абсолютный минимум: минус 0,09141836 при 0° наклонении 290° (19 часов 20 минут) прямого восхождения.
Абсолютный максимум: 0,242047091 при 80° наклонении 125° (8 час 20 минут) прямого восхождения. Всего в выборке для максимума 45 782 объектов.
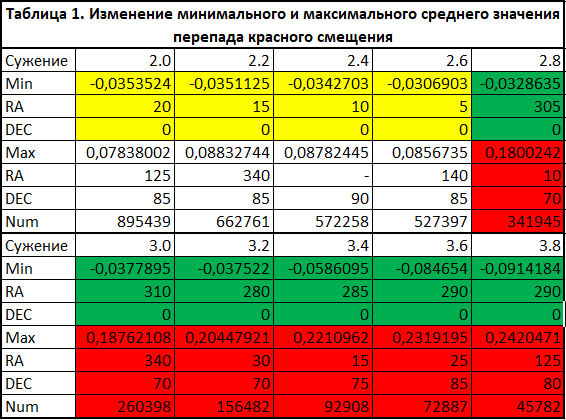
Пояснение к таблице 1. Значение коэффициента сужения 2.0 соответствует ограничению выборки полупространством, ограниченным делящей плоскостью; 2.0 < сужение < 4.0 – выборка ограничена объектами, расположенными внутри области конической формы, получаемой в результате вращения прямой относительно орта, задающего делящую плоскость (90° > угол прямой к орту > 0°, соответственно); 4.0 — выборка ограничена объектами, расположенными на прямой, совпадающей по направлению с ортом, задающим делящую плоскость.
Назовём такой приём фокусировкой.
Повторюсь, физический смысл уменьшения выборки по применённому геометрическому принципу таков, что оно должно усиливать показатели перепада для тенденций, обусловленных относительным движением объектов, если траектория его находится продольно «лучу прожектора».
Получается, что фокусировка — сужение «луча прожектора» — разделяет между собой весомые длительные тенденции, обусловленные относительным перемещением точки наблюдения и протекающие без изменения направления движения. Данный приём делает такие тенденции чётче, снижая их взаимное влияние и затирая иные слабые эффекты.
А если говорить ещё конкретнее, то чем меньше угол траектории движения точки наблюдения к направлению излучения области, попадающей в выборку, тем выше будет фиксируемый средний перепад КС.
Как видно из диаграмм, выраженность жёлтой тенденции с сужением луча угасает, что можно проследить, например, и по изменению значения/направления минимума в таблице 1. Этот процесс теряет выраженность к значению коэффициента сужения 2.8 (соответствует углу ≈70°).
И заменяет его, похоже, именно зелёная тенденция (или близкая ей по направлению), которая к значению коэффициента сужения 3.0 становится, фактически единственной видимой на экваторе, и далее с ростом коэффициента сужения только усиливается, демонстрируя симметрию вращения.
Красная же тенденция также становится менее выраженной на промежутке коэффициента сужения от 2.0 до 2.6 (соответствует углу ≈75°), а затем резко усиливается и дальше только растёт.
Однако же одновременно с этим она, хоть и не меняет направления принципиально, всё же приобретает значительное отклонение направления на точку максимума от значения к значению.
На момент резкого усиления на значении коэффициента сужения 2.8: количество элементов в выборке 341 945, что составляет более трети от общего числа объектов. А перепад среднего значения красного смещения на объект в выборках составляет уже ≈0,18.
Сам факт последовательного увеличения значения среднего перепада КС на объект с сужением выборки говорит в пользу наличия пекулярной скорости точки наблюдения, даже несмотря на некоторое брожение ориентации максимума. В стандартной космологической модели других причин у меня найти не получается.
Таким образом, если интерпретировать это явление как результат наличия пекулярной скорости точки наблюдения относительно трети известных космических объектов, то скорость будет равна ≈27 тыс. км/с (0,18×299 792,458 / 2).
Это уже десятая часть скорости света, и этот факт кажется весьма значительным, но я бы пока не обольщался, ведь, напомню, это результат по полному диапазону красных смещений без учёта масштаба времени.
Изменение диапазона
Глядя на приведённые до сих пор диаграммы, у читателя может сложиться ложное представление о том, что наша Солнечная система несёт пирожки своей бабушке: увеличение угла наклонения делящей плоскости всегда вело к росту перепада красного смещения.
Однако если взять лишь часть диапазона, например, от 1.8 до 2.2 (см. рис. 16), то становится очевидно, что так было не всегда. Красная шапочка надета здесь на экватор.
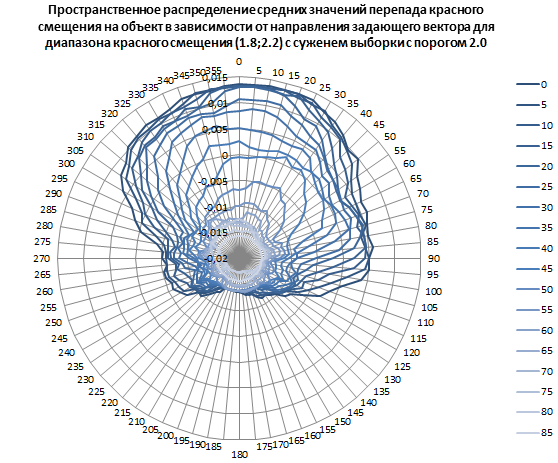
Рис. 16. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для диапазона красного смещения от 1.8 до 2.2 без сужения выборки (с порогом 2.0).
Абсолютный минимум: минус 0,017505519 при 85° наклонении 230° (15 часов 20 минут) прямого восхождения.
Абсолютный максимум: 0,013703 при 0° наклонении 20° (1 час 20 минут) прямого восхождения. Всего в выборке для максимума 14 533 объектов.
Прежде, чем продолжить возводить мыслительные конструкции, ответим на вопрос наиболее внимательных и пытливых читателей:, а произойдёт ли увеличение перепада красного смещения при фокусировке для приведённого диапазона?
Признаться, я делаю запросы параллельно написанию статьи, и на момент написания данных строк не знаю ответа. Не буду строить предположений, давайте просто посмотрим на рисунок 17.
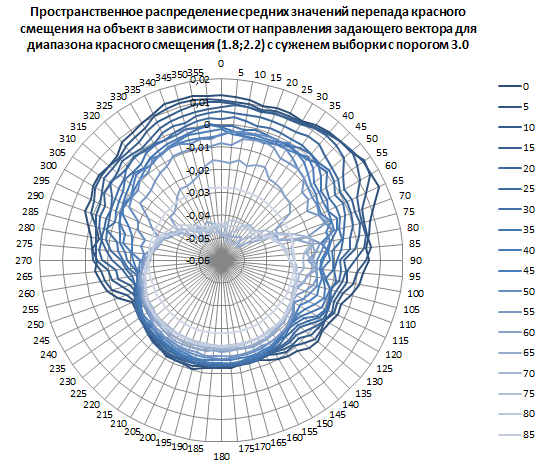
Рис. 17. Пространственное распределение средних значений перепада красного смещения на объект в зависимости от направления задающего вектора для диапазона красного смещения от 1.8
до 2.2 с сужением выборки с порогом 3.0.
Абсолютный минимум: минус 0,051811403 при 65° наклонении 50° (3 часов 20 минут) прямого восхождения.
Абсолютный максимум: 0,016826963 при 5° наклонении 55° (3 часа 40 минут) прямого восхождения. Всего в выборке для максимума 6 983 объектов.
Увеличение есть, но при этом ощутимо меняется направление при общем сохранении формы. Причина такой конфигурации данных может скрываться в кривизне траектории движения, если это движение, лежащего в основе красной тенденции. Вероятно, это течение с очень большим радиусом.
Мы к этому ещё вернёмся, а пока резюмирую: величина красной тенденции, полученная в результате фокусировки (в конце предыдущей главы), в результате полного учёта траектории точки приёма — Солнца — относительно Стрельца-А, вероятно, будет ещё значительнее.
Поговорим об этом развёрнуто.
Эффект памяти КС
Как я уже писал ранее, те цветные тенденции, что мы видели на рисунке 4, имеют характер, зависящий как от скорости точки в момент приёма, так и от перемещения её в прошлом.
На величину абсолютного значения красного смещения в общем случае влияет несколько факторов:
- пекулярная скорость источника, которая в применённой методике никак не учитывается, а принимается как неизбежная погрешность (скорость движения Солнечной системы относительно объектов собственной галактики на порядок меньше, чем, например, выявленный перепад по красной тенденции);
- гравитационный потенциал точек наблюдения и приёма, который также методикой совершенно не учитывается в связи с ещё меньшим влиянием, чем у пекулярных скоростей;
- скорость и направление движения точки наблюдения в момент приёма;
- и, наконец, скорость и направление движения точки наблюдения относительно удалённого временного диапазона, которые можно выделить за счёт нелинейно меняющегося масштаба.
Именно этот последний фактор нас интересует. Его наличие создаёт предпосылки для отслеживания траектории точки наблюдения с помощью относительного (сравниваемого с аналогичным) красного смещения окружающего излучения.
Как в примере из фильма BBC с каплей красителя, растворённой в раковине. Досконально зная состояния всех физических частиц в раковине, можно ретроспективно восстановить как давно, под каким углом, с какими скоростью и ускорением и прочее в раковину попала капля с красителем. Даже если к настоящему моменту её молекулы равномерно распределились среди прочих.
Так и пространственное перемещение точки приёма записано во всё более дальних областях излучения в виде влияния относительного перемещения на красное смещение. Причём, и на геометрическое смещение, и на пространственную ориентацию.
Упрощённо эффект показан на следующем рисунке 18.
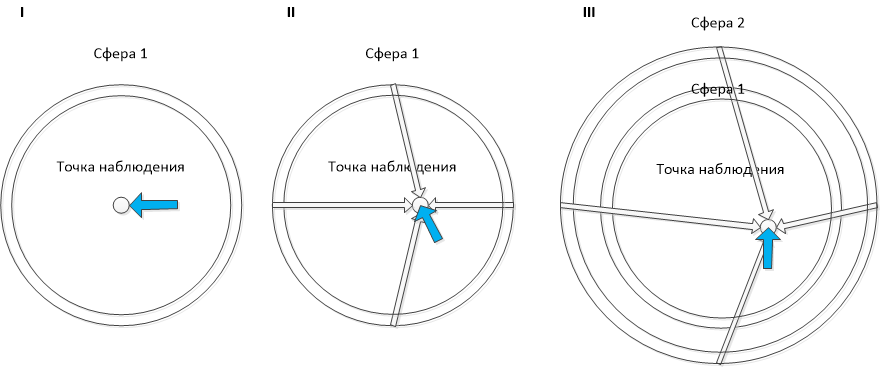
Рис. 18. Эффект «памяти» красного смещения космического излучения.
- Возьмём некоторую условную сферу 1 и точку наблюдения. Понятие сфера очень условно, потому что в части определения расстояния до её точек от центра мы опираемся на тот же показатель, который используем в сравнении для определения перепада — неоднородности — красного смещения. То есть, в итоге, радиусы сферы измеряются в показателе красного смещения, а сама сфера — это выборка всех объектов в определённом диапазоне красных смещений. Даже при этом пространственная неоднородность вполне различима для достаточно узких диапазонов.
- Относительно излучения сферы 1 пространственное распределение среднего перепада красного смещения на объект таково как если бы точка наблюдения была расположена и ориентирована со смещением от геометрического центра сферы 1, потому что двигалась в определённом направлении и с определённой скоростью всё то время, пока излучение объектов сферы 1 её достигнет.
- Сфера 2 — сфера большего радиуса, чем сфера 1, но с таким же диапазоном. Относительно её излучения пространственное распределение среднего перепада красного смещения на объект покажет предыдущее положение и ориентацию точки наблюдения.
Это пока только гипотеза и задел для следующей статьи.
Итак, на рисунке 4, фактически, отображены основные усреднённые тенденции для полного диапазона значений красного смещения, что означает их относительное постоянство на большом промежутке существования видимого космоса.
Два безусловных претендента на пространственные перемещения, формирующие такие возмущения «поля красного смещения» (я позволю себе далее работать с ним как с полем, сокращённо — ПКС) как на рисунке 4 — это вращение солнечной системы вокруг Стрельца-А и циклическое смещение солнечной системы вверх-вниз относительно галактического экватора.
Ориентировочный период первого — 190–250 миллионов лет (разные источники и орбиты), второго — 33 миллиона лет.
Размер красной даже без учёта выявленного вращения, то есть без учёта того, что на полной диаграмме она размазана, в разы превышает внутригалактические скорости солнечной системы, что говорит о её длительности и относительном постоянстве. Поэтому предположим, что зелёная и жёлтая тенденции — результат внутригалактического движения солнечной системы. Нам необходимо с ними разобраться, чтобы затем, оценив их траектории и скорости, пересчитать диаграммы относительно Стрельца-А.
В конечном итоге, это должно позволить рассмотреть движение галактики Млечный путь относительно дальнего космоса.
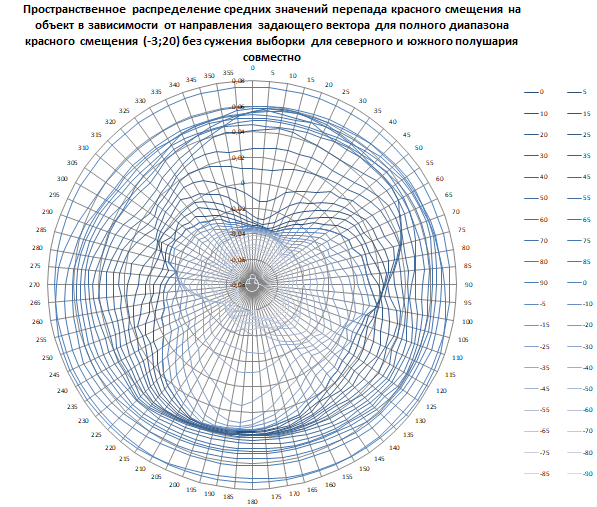
Рис. 19. Совмещённая общая диаграмма перепада средних значений красного смещения на объект для северного и южного полушарий.
На рисунке 19 для наглядности показаны пространственные контуры перепада значений КС для северного и южного полушарий, хотя контуры южного полушар
