[Из песочницы] История одного диплома или как сделать шаробота26.07.2016 18:03

История этого проекта начинается в 2014 году, когда я учился на 4-м курсе в ведущем техническом вузе России на кафедре «Робототехнические системы». В это время я уже начал задумываться над темой диплома и искал проект, который был бы интересен мне, и при этом в нем присутствовала некоторая новизна. И вот однажды, увидев видео шаробота Rezero, я захотел попробовать повторить успех. Кому интересно, что из этого получилось — прошу под кат.

Введение

В начале хотелось бы поговорить о достоинствах шаробота. Благодаря единственной точке контакта с поверхностью, шаробот одинаково легко передвигается во всех направлениях, являясь чрезвычайно подвижным и манёвренным, по сравнению с обычными колесными роботами. Манёвренность шаробота ограничена только его динамикой, в отличие от механических ограничений, налагаемых колёсами (например, невозможность движения боком).

Следующее важное достоинство — робот может быть высоким, и чем выше он будет, тем он будет устойчивее. Почему устойчивее? Это видно из уравнения динамики обратного маятника. Ускорение отклонения от вертикального положения равновесия обратно-пропорционально расстоянию до центра масс, т.е. более высокий обратный маятник будет медленнее падать. Это снижает требования к скорости реакции системы управления, но, возможно, увеличивает момент, который должны развивать привода.

Еще одно преимущество — он может ездить по наклонным и подвижным поверхностям, например, палуба корабля или пол самолета при взлете. Да и согласитесь, движется он гораздо красивее, чем обычные колесные роботы.

Один из главных недостатков шаробота — возможность потери вертикального положения равновесия. Но лично я думаю, что это вполне решаемая инженерная задача. Инженеры роботов Aido и Mobi решили ее следующим образом: при превышении некоторого угла отклонения выдвигаются «ноги», чтобы робот не потерял устойчивость.

Мой рассказ состоит из следующих частей:
— Математическая модель
— Разработка алгоритмов управления
— Конструкция
— Аппаратно-программное обеспечение
— Результаты

1 Математическая модель

Вывод уравнений движения необходим для дальнейшего синтеза управления и моделирования движения. В этом разделе будет немного математики и механики.

На данный момент все существующие математические модели шаробота составлены с учетом некоторых упрощений с помощью уравнений Лагранжа 2-го рода. А так как шаробот является неголономной механической системой, то применять уравнения Лагранжа 2-го рода к такой систему некорректно. В роботе CMU модель шаробота рассматривается как три независимые плоские модели, тем самым не учитывается взаимовлияние этих моделей. В Rezero разработали трехмерную математическую модель, в которой не учитываются гироскопические эффекты, возникающие при вращении омниколес.

Я поставил цель создать наиболее полную математическую модель робота с минимальным количеством допущений. В достижении этой цели мне помог мой научный руководитель С.Л. Крутиков, за что я выражаю ему огромную благодарность.

1.1 Кинематика

Для кинематического описания системы я ввел подвижные системы координат, показанные на рисунке.

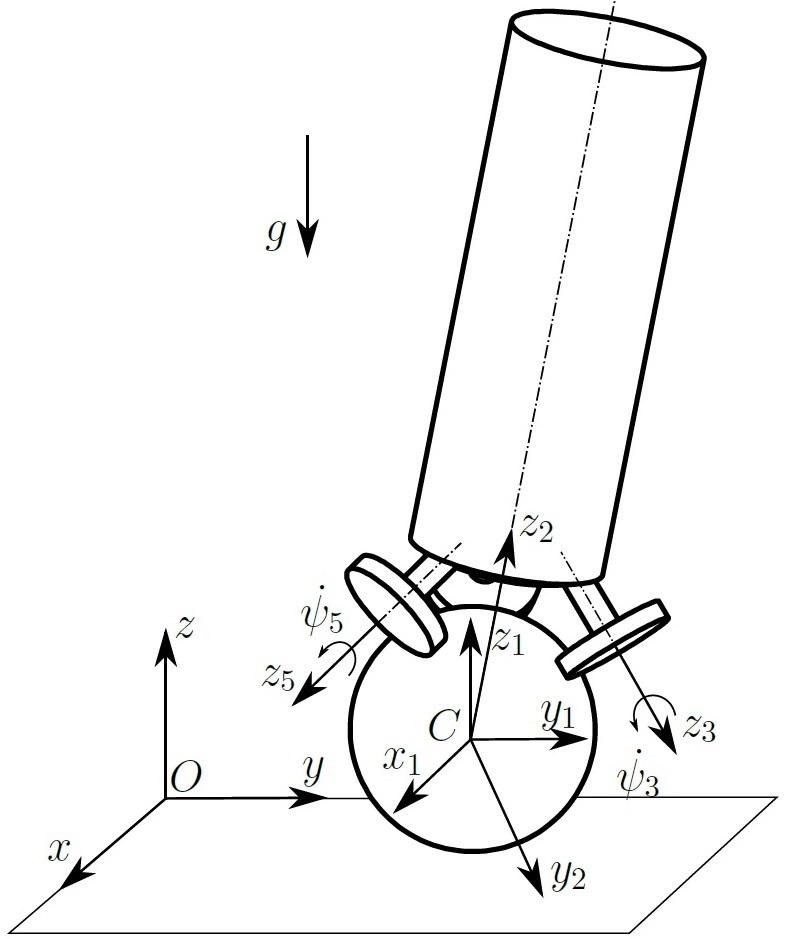
Инерциальная система координат обозначена как $xyz$ . Система координат $x_1y_1z_1$ находится в центре шара. Для перехода от инерциальной системы отсчёта к центру шара используется следующая однородная матрица:

$\begin{equation*} \m{A}_c=\begin{pmatrix} \nonumber 1 & 0 & 0 & x \\ 0 & 1 & 0 & y\\ 0 & 0 & 1 & r_{ball} \\ 0 & 0 & 0 & 1 \end{pmatrix}, \end{equation*}$

где $x$ и $y$ смещение центра шара вдоль оси $x$ и $y$ соответственно.

Для описания вращения шара удобно использовать кардановы углы или углы Tait–Bryan. Таким образом, система координат $x'_1y'_1z'_1$ , связанная с шаром, получается путем поворота $Cx_1y_1z_1$ на углы $\varphi_{x}$ , $\varphi_{y}$ и $\varphi_{z}$ вокруг осей $x_1, y_1$ и $z_1$ соответственно. Данную последовательность поворотов можно представить в виде произведения матриц поворота:

$\begin{equation*} \label{eq:m_rotaion_ball} \m{R}_{\varphi} = \m{R}_x(\varphi_x) \m{R}_y(\varphi_y) R_z(\varphi_z). \end{equation*}$

Аналогично можно описать вращение тела шаробота в пространстве. Система координат $x_2y_2z_2$ 2-го звена, связанная с телом, получается путем поворота $x_1y_1z_1$ на углы $\vartheta_{x}$ , $\vartheta_{y}$ и $\vartheta_{z}$ вокруг осей $x_1, y_1$ и $z_1$ соответственно. Данную последовательность поворотов также можно представить в виде произведения матриц поворота:

$\begin{equation} \label{eq:m_rotaion_body} \m{R}_{\vartheta} = \m{R}_x(\vartheta_{x}) \m{R}_y(\vartheta_{y}) \m{R}_z(\vartheta_{z}). \nonumber \end{equation}$

3-я, 4-ая и 5-ая системы координат связаны с омниколесами. Чтобы перейти от системы координат тела к системе координат омниколеса требуется выполнить ряд элементарных преобразований (два поворота, перенос, затем опять поворот), я не буду их описывать здесь.

Последовательность переходов представлена в виде следующего кинематического графа:

Для описания положения системы используется следующий вектор обобщенных координат:

$\begin{equation} \ve{q}=(x, y, \varphi_x, \varphi_y, \varphi_z, \vartheta_x, \vartheta_y, \vartheta_z, \psi_1, \psi_2, \psi_3)^T, \nonumber \end{equation}\\$

где $x, y$ — координаты центра шара, $\varphi_x, \varphi_y, \varphi_z, \vartheta_x, \vartheta_y, \vartheta_z$ — кардановы углы, описывающие вращение шара и тела соответственно, $\psi_1, \psi_2, \psi_3$ — углы поворота омниколеса вокруг оси двигателя.

1.2 Динамика

Исходя из неголономности системы было принято решения использовать уравнения Аппеля для составления дифференциальных уравнений движения шаробота.

На систему наложено 6 неголономных связей: три связи качения омниколес по шару, две связи для скорости центра шара и одна связь отсутствия верчения шара. Таким образом, число обобщенных координат m=11, число связей s=6, а число степеней свободы n=5. Будем использовать следующий вектор псевдоскоростей:

$\begin{equation*} \bm{\dot{\pi}} = (\dot{x}, \dot{y}, \dot{\vartheta_x}, \dot{\vartheta_y}, \dot{\vartheta_z})^T. \end{equation*}$

Для составления уравнений движения необходимо вычислить энергию ускорений для каждого звена:

$\begin{equation*} S= \sum\limits_{i=1}^N \frac{1}{2} \cdot tr( \ddot{\m{T}}_{i} \m{H}_{i} \ddot{\m{T}}^\m{T}_{i}}), \end{equation*}$

где $N$ — количество звеньев, $\m{T}_{i}$ — матрица перехода от инерциальной системы координат к системе координат $i$ -го звена, $\m{H}_{i}$ — матрица инерции $i$ -го звена, а $tr$ — след матрицы. В общем случае $S$ является функцией от $\ddot{q}_1,...,\ddot{q}_m, t$ . С помощью уравнений связи энергия ускорений сводится к функции, зависящей только от $\ddot{\pi}_1,...,\ddot{\pi}_n, t$ .

Массо-инерционные параметры

Матрица инерции шара имеет диагональный вид, т.к. оси системы координат $Ox_1y_1z_1$ являются главными центральными осями инерции:

$\begin{equation*} \m{H}_{1}=\begin{pmatrix} %\nonumber I_{1,xx} & 0 & 0 & 0\\ 0 & I_{1,yy} & 0 & 0\\ 0 & 0 & I_{1,zz} & 0\\ 0 & 0 & 0 & m_{1} \end{pmatrix}. \end{equation*}$

Т.к. плоскости $Cx_2z_2$ и $Cy_2z_2$ являются плоскостями симметрии тела, центробежные моменты инерции $I_{xy}, I_{xz}$ и $I_{yz}$ равны нулю. Матрица инерции тела будет иметь следующий вид:

$\begin{equation*} \m{H}_{2}=\begin{pmatrix} %\nonumber I_{2,xx} & 0 & 0 & 0 \\ 0 & I_{2,yy} & 0 & 0 \\ 0 & 0 & I_{2,zz} & m_{2} \cdot l \\ 0 & 0 & m_{2} \cdot l & m_{2} \end{pmatrix}, \end{equation*}$

где $l$ — расстояние от центра шара до центра масс тела вдоль оси $Cz_2$ .

Матрица инерции омниколес имеет диагональный вид, т.к. оси системы координат омниколеса образуют плоскости симметрии:

$\begin{equation*} \m{H}_{3,4,5}=\begin{pmatrix} %\nonumber I_{w, xx} & 0 & 0 & 0 \\ 0 & I_{w, yy} & 0 & 0\\ 0 & 0 & I_{w, zz} & 0 \\ 0 & 0 & 0 & m_{wheel} \end{pmatrix}. \end{equation*}$

В приведенном моменте инерции $I_{w,zz}$ необходимо также учесть момент инерции ротора двигателя:

$I_{w,zz} =I'_{w,zz} + i^2 \cdot I_{\text{рот}},$

где $i$ — передаточное число редуктора.

Дифференциальное уравнение движения Аппеля в псевдокоординатах:

$\begin{equation} \label{eq:appel} \frac{\partial{S}}{\partial{ \boldsymbol{\ddot{\pi}} }} = \m{Q}_1 + \m{Q}_2, \end{equation}$

где $\m{Q}_1$ — обобщенная сила от моментов приводов, $\m{Q}_2$ — обобщенная сила от сил тяжести.

Записываем уравнения Аппеля в матричной форме и решаем относительно $\ddot{\pi}$ :

$\begin{equation*} \boldsymbol{\ddot{\pi}} = \m{A}^{-1}(\boldsymbol{\ve{q}}) (\m{Q}_{1} - \boldsymbol{b(\ve{q}, \dot{\pi})} - \boldsymbol{c(\ve{q})}) \end{equation*}$

Чуть-чуть подробнее

Уравнения движения можно записать в матричной форме

$\begin{equation*} \boldsymbol{f}(\boldsymbol{q}, \boldsymbol{\dot{\pi}}, \boldsymbol{\ddot{\pi}}, \boldsymbol{\tau}, t) = \m{A}(\boldsymbol{q}) \boldsymbol{\ddot{\pi}} + \boldsymbol{b}(\boldsymbol{q}, \boldsymbol{\dot{\pi}}) + \boldsymbol{c}(\boldsymbol{q}) - \m{Q}_1 = 0, \end{equation}$

где

$\begin{equation*} \m{A}(\boldsymbol{q}) = \frac{\partial{\boldsymbol{f}}}{ \partial{\boldsymbol{\ddot{\pi}}} }, \\ \boldsymbol{b}(\boldsymbol{q}, \boldsymbol{\dot{\pi}}) = \boldsymbol{f} - \m{A} \cdot \boldsymbol{\ddot{\pi}}, \\ &\boldsymbol{c}(\boldsymbol{q}) = - \m{Q}_{2}. \end{equation*}$

Все вычисления выполнялись символьно с помощью Maple. Затем полученные уравнения были перенесены из Maple в Matlab для моделирования.

2 Разработка алгоритмов управления

Еще немного теории управления и матчасть на этом закончится. В теории управления хорошо развиты методы анализа линейных систем. Для вполне наблюдаемых систем наиболее часто применяется оптимальное управление с квадратичным функционалом (линейно-квадратичный регулятор, LQR), которое гарантирует стабилизацию системы в случае, если система вполне управляема. Шаробот является вполне наблюдаемой системой, т.к. вектор состояния может быть полностью измерен. Вычислив ранг матрицы управляемости, я также убедился в управляемости системы.

Для получения линейно-квадратичного регулятора в начале необходимо линеаризовать систему в окрестности вертикального положения неустойчивого равновесия $\boldsymbol{q} = 0, \boldsymbol{\dot{\pi}} = 0, \boldsymbol{\ddot{\pi}} = 0$

$\begin{equation*} \boldsymbol{\dot{x}} &= \m{A} \cdot \boldsymbol{x} + \m{B} \cdot \boldsymbol{u}, \nonumber \\ \boldsymbol{y} &= \m{C} \cdot \boldsymbol{x} + \m{D} \cdot \boldsymbol{u}, \nonumber \\ \boldsymbol{x} &= (x, y, \vartheta_x, \vartheta_y, \vartheta_z, \dot{x}, \dot{y}, \dot{\vartheta_x}, \dot{\vartheta_y}, \dot{\vartheta_z})^T, \nonumber \\ \m{C} &= \m{E}_{10}, \quad \m{D} = 0. \nonumber \end{equation*}$

Вектор $\boldsymbol{x}$ — вектор состояния или фазовый вектор, $\boldsymbol{y}=\boldsymbol{x}$ — вектор измерения и $\boldsymbol{u}=(\tau_1, \tau_2, \tau_3)^T$ — управление (моменты приводов).

LQR регулятор имеет следующий критерий оптимальности:

$\begin{equation*} \label{eq:cost} \m{J} = \int\limits_{0}^{\infty}(\boldsymbol{x}^T \m{Q} \boldsymbol{x} + \boldsymbol{u}^T \m{R} \boldsymbol{u})dt, \end{equation*}$

где $\m{Q}$ и $\m{R}$ — положительно определённая матрица. Задача минимизации данного функционала сводится к решению матричного алгебраического уравнения Риккати:

$\begin{equation*} \label{eq:ricatti} \Phi \cdot \m{B} \cdot \m{R}^{-1} \cdot \m{B}^T \cdot \Phi - \Phi \cdot \m{A} - \m{A}^T \cdot \Phi - \m{Q} = 0. \end{equation*}$

Для линейно-квадратичного регулятора управление записывается в виде $\boldsymbol{u}=-\m{K}\boldsymbol{x}$ , где $\m{K}=\m{R}^{-1}\m{B}\Phi$ , $\Phi$ — решение уравнения Риккати. В итоге мы имеет матрицу коэффициентов обратной связи:

$\begin{equation*} \m{K} = \begin{pmatrix} 0 & -1.0 & 9.63 & 0 & -0.7 & 0 & -1.34 & 1.88 & 0 & -0.18 \\ 0.86 & 0.5 & -4.81 & 8.34 & -0.7 & 1.16 & 0.67 & -0.9 & 1.63 & -0.18 \\ -0.86 & 0.5 & -4.81 & -8.34 & -0.7 & -1.16 & 0.67 & -0.9 & -1.63 & -0.18 \\ \end{pmatrix}. \nonumber \end{equation*}$

При умножении данной матрицы на вектор состояния $\boldsymbol{x}$ мы получим три момента, которые необходимо подать на двигатели для стабилизации системы. LQR является PD регулятором, в случае если вектор состояния состоит из координат и их производных. Как вы понимаете, использовать обычный PID регулятор и подбирать коэффициенты вручную в такой системе почти невозможно.

Модель в Matlab simulink c трехмерной визуализацией

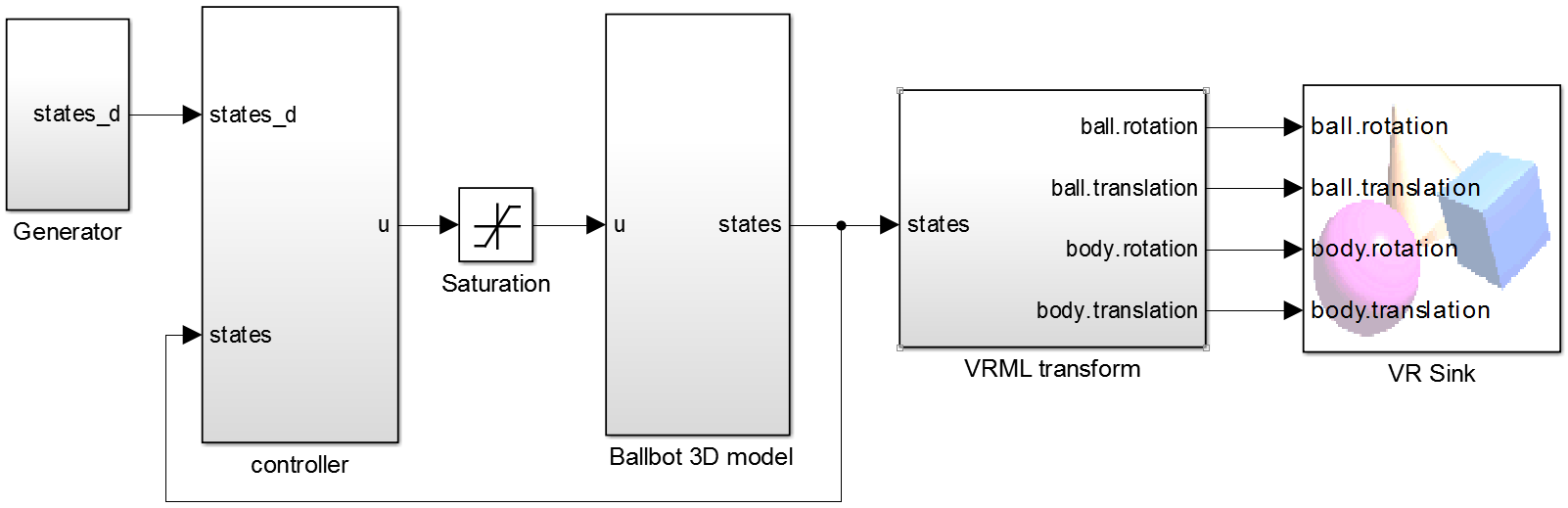
Дам небольшие пояснения к каждому блоку. В блоке «Ballbot 3D model» реализованы уравнения Аппеля. На вход подается управление $\boldsymbol{u}$ (три момента), на выходе получается вектор состояния $\boldsymbol{x}$ (см. п.2).

Блок «VRML transform» преобразует вектор состояния в координаты для визуализации. «VR Sink» содержит модель в формате vrml и именно этот блок отрисовывает графику.

На вход блоку «controller» подается вектор состояния $\boldsymbol{x}$ и желаемый вектор состояния $\boldsymbol{x}_d$ , с помощью которого можно задавать траекторию движения и скорость. Блок производит элементарное уможножение матриц для получения трех моментов $\boldsymbol{u}=-\m{K}(\boldsymbol{x}-\boldsymbol{x}_d)$ .

Так как момент, который развивают привода, ограничен, я добавил звено насыщения (saturation).

Для трехмерной визуализации была сделана простая модель шаробота в SolidWorks. Затем она была экспортирована в формате vrml и добавлена в блок VR Sink.

Результаты моделирования при начальном отклонении в 10 градусов

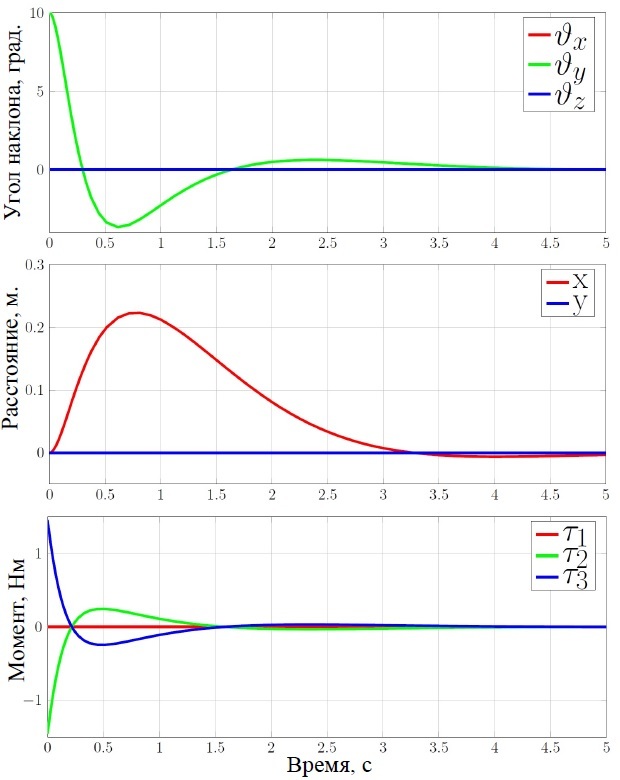
3 Конструкция

Конструкция робота разработана в CAD системе Siemens NX. На основании построенной модели были определены массовые и инерционные характеристики звеньев робота.

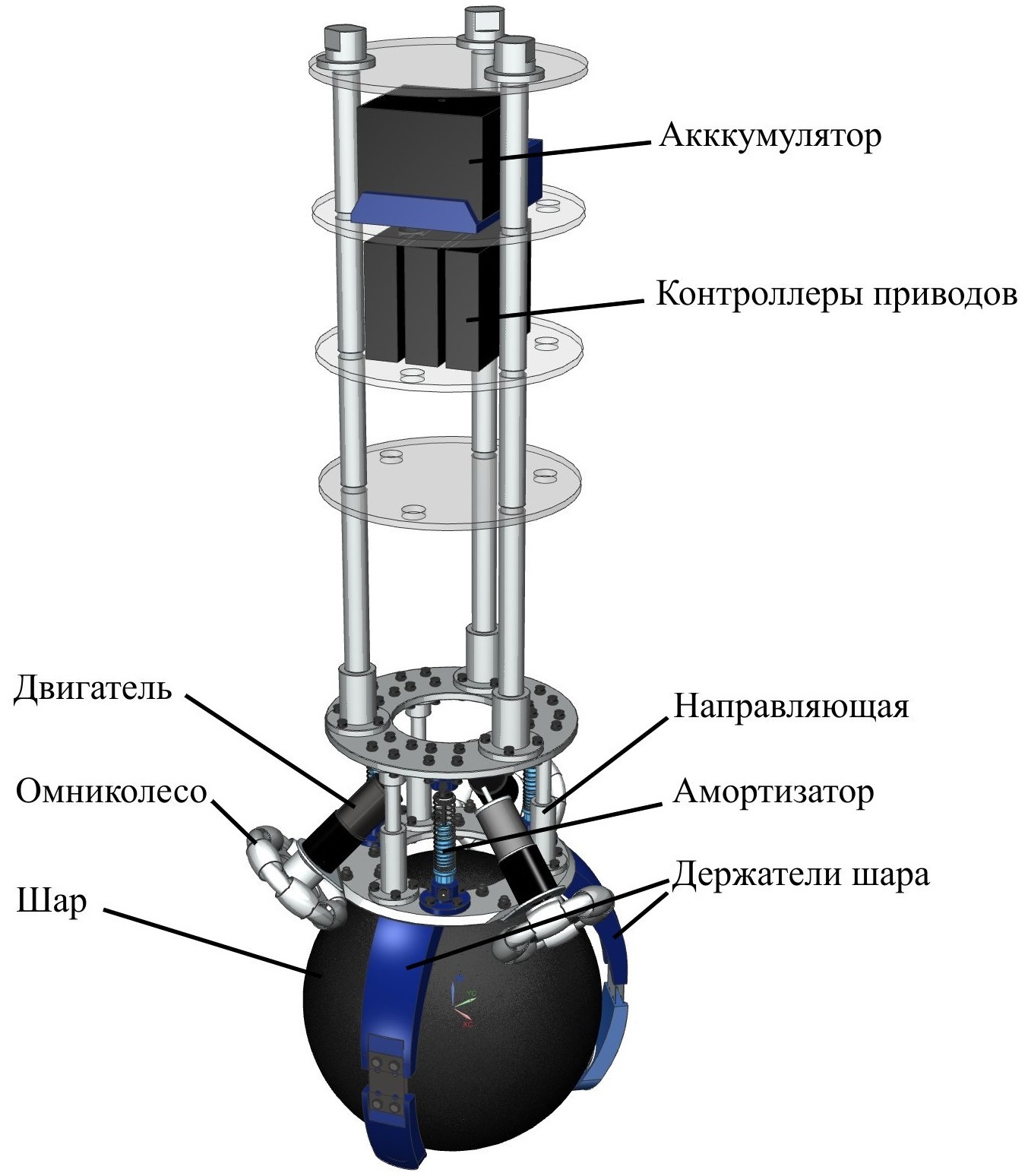
Конструкция состоит из двух алюминиевых оснований. На нижнем основании закреплены три двигателя, которые приводят в движение омниколеса. Верхнее основание крепится к нижнему с помощью амортизаторов и направляющих. Задача амортизаторов заключалась в уменьшении вибраций верхней части корпуса, где находится вся электроника, правда на практике это не помогло.

Полки сделаны из оргстекла для облегчения конструкции. На них располагается вся бортовая электроника: аккумулятор, контроллеры приводов, микроконтроллер, инерциалка и др.

В качестве шара используется баскетбольный мяч диаметром 240 мм. Держатели шара прижимают его к омниколесам, тем самым увеличивают трение. К сожалению, их не получилось изготовить, так как на нашей кафедре нет 3D принтера, а печатать на заказ дорого, т.к. они не маленькие и коэффициент заполнения нужен большой для прочности.

Омниколеса были приобретены на Aliexpress по 120$ за штуку. Самая дорогая часть робота, после приводов, конечно.

Все металлические детали изготовлены из дюралюминия на заказ на одном Московском заводе. На этом же заводе нам сделали полки из оргстекла. Заказ вышел на сумму 30 000р, примерно.

Немного фотографий сборки с комментариями

Друг помог мне развести плату, на которой находятся DC-DC преобразователь, IMU и логический преобразователь уровней для I2C. Сверху втыкается ODROID

Это самый первый вариант конструкции с приводами Dynamixel MX64. Коробки для приводов напечатаны.

Амортизаторы фирмы HSP для радиоуправляемых моделей с масштабом 1:10.

В таком виде я получил комплект приводов и контроллеров.

Чтобы надеть омниколесо на вал двигателя пришлось вытачивать втулку.

Это уже финальный результат.

4 Аппаратно-программное обеспечение

Почти все аппаратные компоненты шаробота представлены на функциональной схеме. Скажу пару слов про каждый элемент, двигаясь «снизу вверх».

4.1 Привода и контроллеры приводов

Всех сложнее было найти привода и контроллеры приводов. На выходе LQR регулятора у нас момент, следовательно надо иметь контроллер с возможностью управления по току (т.е. по моменту). Видимо, эта задача встречается очень редко в повседневной жизни, и я нашел только одно доступное по деньгам решение — Dynamixel. Мы купили и попробовали привода Dynamixel MX64, в которых есть режим управления по току. К сожалению, их быстродействия не хватало для стабилизации робота.

Я уже было потерял надежду на создание реального шаробота, но к счастью мне помог Ярослав из НУЦ «Робототехника» и предоставил на некоторое время три привода Maxon с контроллерами, за что я ему очень благодарен. В итоге у меня оказался бесколлекторный двигатель постоянного тока Maxon EC-max 30 40Вт со следующими характеристиками:

Номинальное напряжение 24В
Номинальная скорость вращения 7220 об/c
Номинальный момент 33.8 мНм
Удерживающий момент 160 мНм

Планетарный редуктор Maxon GP 32 с передаточным числом n=14 и контроллер привода Maxon EPOS 24/5, который имеет режим управления по току.

Как вы можете заметить, привода не очень мощные и передаточное число маленькое, поэтому момента на выходе едва ли хватает для стабилизации шаробота. У Rezero, например, используются двигатели 200Вт и редуктор с передаточным числом 51.

4.2 Микроконтроллер, инерциальный модуль, трансивер

В качестве микроконтроллера я использовал STM32F4-Discovery, который имеет необходимые нам интерфейсы: CAN, UART и I2C. Он получает данные с гироскопа и акселерометра по I2C и энкодеров по шине CAN. На основе полученных данных рассчитывает управление и отправляет задание на контроллеры приводов по шине CAN. Чтобы не реализовывать протокол для связи с EPOS контроллерами самому, я использовал библиотеку libepos. Для того, чтобы подключить STM’ку к CAN сети необходим приемопередатчик CAN (трансивер) за 4$.

В качестве инерциального модуля я использовал плату GY-521 за 3$ на основе микросхемы MPU6050, которая включает в себя 3-х осевой гироскоп и 3-х осевой акселерометр. Для обработки показаний этих датчиков я использовал фильтр Маджвика, который в последнее время так полюбили коптероводы.

Для упрощения разработки под STM я использовал STM32Cube HAL (hardware abstraction layer).

Частота на которой работает управление равна примерно 300 Гц, т.е. 300 раз в секунду мы считываем показания всех датчиков, рассчитываем управление и отправляем задание на привода. Все это происходит в бесконечном цикле, который можно представить в виде следующего псевдокода:

int main()
{
    initialize_imu();/* инициализация IMU по I2C */
    initialize_motors(); /* инициализация двигателей по CAN */

    while (1) {     
        read_imu(); /* чтение и фильтрация данных IMU */
        get_omniwheels_speed(); /* чтение данных энкодеров по CAN */

        /* поступила команда по UART от odroid */
        if (uart_rx_flag) {
            uart_rx_flag = 0;

            struct joystick_data* joystick = (struct joystick_data*)UARTdev_Get_RX_buf();
            process_joystick_input(joystick);
        }

        calculate_control(); /* вычисление управления */
        set_torque(); /* отправка задания на привода по CAN */
    }
}

4.3 Одноплатный компьютер, аккумулятор, DC-DC преобразователь, джойстик

Бортовой одноплатный компьютер ODROID U3 принимает данные от джойстика через Bluetooth адаптер и передает их на микроконтроллер через UART. На нем установлена операционная система lubuntu c Linux ядром 3.8.13.26-rt31 c поддержкой реального времени.

Свинцово-кислотный аккумулятор Delta 12045 ёмкостью C = 4.5 Ач. Его хватает примерно на час работы.

Напряжение питания одноплатного компьютера Odroid-U3 5В, максимальный потребляемый ток 2А.Т. к. источник питания 12В, необходим понижающий LM2596S DC-DC преобразователь за 2$.

Для управления шароботом используется Bluetooth джойстик Terios. Джойстик передает команды по Bluetooth на ODROID, в котором стоит Asus USB-BT400 адаптер. Для чтения команд джойстика я использовал следующую библиотеку. Поступившая команда парсится, пакуется и отправляется по UART на STM32, где на прием каждого байта происходит прерывание.

Так же к ODROID можно подключится по SSH. При запуске одройд создает Ad-hoc сеть через WiFi адаптер.

Результаты

Итого у меня получилось собрать работающего шаробота и защитить диплом. На реализацию этого проекта у меня ушло ровно 2 года. Скажем так, у меня не получилось приблизиться к результатам Rezero, так как у меня не было таких человеческих и финансовых ресурсов как у студентов из Швейцарии. Думаю, если бы были более мощные двигатели и более продвинутый инерциальный модуль, то результаты были бы на порядок лучше.

Исходный код я не открываю по некоторым причинам. Если хотите знать детали реализации — напишите мне, я с удовольствием поделюсь с вами кодом индивидуально. Двигатели пришлось вернуть и на данный момент «железяка» стоит без них. Возможно, проект будет дальше развиваться студентами, если найдутся подходящие движки и найдутся желающие. Например, было бы интересно разработать нелинейные алгоритмы управления.

Я достаточно поверхностно рассказал про процесс разработки, так что буду рад ответить на ваши вопросы.