[Из песочницы] Дифференциальная геометрия кривых. Часть 1
Предисловие
Привет всем читателям. Просто решил написать статью о дифференциальной геометрии кривых. На мой взгляд, тема из «непрерывной» математики будет большинству читателей Хабра полезна, по крайней мере ближайший час =), учитывая что это IT ресурс, а IT это где то ближе к дискретной математике (опять таки на мой несовершенный взгляд). Но кое где, знаю точно есть не только дискретка, например, CAD системы проектирования имеют движки построенные на дифференциальной геометрии (ну конечно, не на одной лишь, и вычислительная геометрия там есть и прочее). Возможно в играх используется, я не знаю. Ведь игра — это обычно движение, а чтобы описать движение — хорошо бы знать геометрию.
Введение
Дифференциальная геометрия кривых (как понятно из названия) занимается геометрией кривых, но методами дифференциального исчисления, или матанализа.
Для тех, кто кривые задавал только на плоскости, в таком виде:
$$display$$ y = ax + b $$display$$
или тому подобное:
$$display$$ y = \frac{1}{\sigma\sqrt{2\pi}} \exp\left (-\frac{(x-\mu)^2}{2\sigma^2}\right) $$display$$
даже так (неявное задание):
$$display$$ y^{3}x = 7x^{2} + 4 $$display$$
скажу, что это не лучший способ, то есть не универсальный, а может неудобен (для пространств большей размерности). Можно конечно и так, для своих задач будет хорошо, но в общем виде кривые задают в параметрической форме. Потому что, если подобным образом задавать уже в 3D пространстве, получится нечто вроде:
\begin{equation*}
\begin{cases}
z=2x-y,
\\
z= x^{2}+y^{2}
\end{cases}
\end{equation*}
а то и так:
\begin{equation*}
\begin{cases}
z=2x-y,
\\
y= x^{2}+z^{2}
\end{cases}
\end{equation*}
Что можно интерпретировать как пересечение двух произвольных поверхностей. Именно пересечение нам и задает пространственную кривую. И еще примерчик окружности:
\begin{equation*}
\begin{cases}
x^{2}+y^{2}+z^{2}=1,
\\
x+y+z=1
\end{cases}
\end{equation*}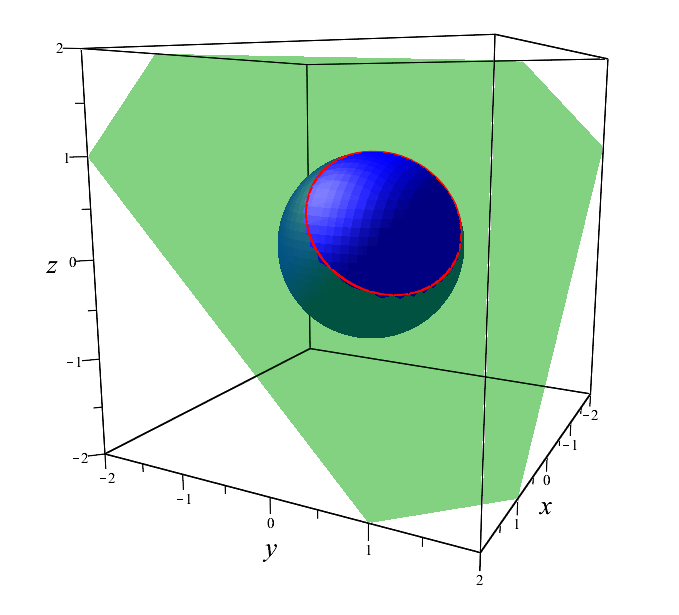
Картинка для лучшего восприятия того что происходит при пересечении
А вы спросите почему эти способы подобны. Ну смотрите, в плоскости мы имеем в общем виде неявное задание кривой $inline$F (x, y)=0.$inline$ Тогда в 3D пространстве, по аналогии, хочется записать уравнение, добавив одну координату $inline$F (x, y, z)=0.$inline$ Но это всё равно получается не кривая, а поверхность. Тогда если добавить еще одно уравнение, получается система, или две поверхности:
\begin{equation}
\begin{cases}
F (x, y, z)=0,
\\
G (x, y, z)=0.
\end{cases}
\end{equation}
которые, вообще говоря, могут и не пересекаться, потому произвольные $inline$F$inline$ и $inline$G$inline$ не всегда дадут кривую.
А потому давайте уже скорее перейдем к параметрическому заданию кривых.
Параметрическое задание кривой
«Задать кривую параметрически» означает задать координату каждой точки кривой. То бишь, каждая координата по-отдельности будет функцией от общего параметра.
\begin{equation*}
\begin{cases}
x = x (t),
\\
y = y (t),
\\
z = z (t).
\end{cases}
\end{equation*}
Эту штуку обычно называют радиус вектором $inline$\vec{r}(t) = (x, y, z).$inline$ Или, если быть точнее, правильней так:
$$display$$\vec{r}(t) = (x, y, z)^{T}=\begin{bmatrix} x \\ y \\ z \end{bmatrix} $$display$$
Обычный вектор — это вектор-столбец, или транспонированный вектор-строка. Если еще вдаваться в дебри тензорного анализа, то вектор-столбец = вектор, а вектор-строка = ковектор. Но нам это не суть важно, потому что всё равно в ортогональном нормированном базисе, в коем мы и работаем, разница между ними исчезает. Дальше я буду записывать вектора в строку, это ни на что не влияет, зато компактно получается.
Кстати, если взглянуть на систему 1, и для удобства обозначив, например, $inline$z=t$inline$:
\begin{equation*}
\begin{cases}
F (x, y, t)=0,
\\
G (x, y, t)=0.
\end{cases}
\end{equation*}
то формально решив эту систему уравнений относительно $inline$x, y$inline$, получим решение зависящее от параметра $inline$ \{x (t), y (t)\} $inline$. А теперь, если всё объединить в один вектор:
\begin{equation*}
\begin{cases}
x = x (t),
\\
y = y (t),
\\
z = t,
\end{cases}
\end{equation*}
получаем некоторую параметризацию кривой, до недавнего времени заданной как пересечение поверхностей.
Ну хорошо, например, винтовая линия:
\begin{equation*}
\begin{cases}
x = cos (t),
\\
y = sin (t),
\\
z = t
\end{cases}
\end{equation*}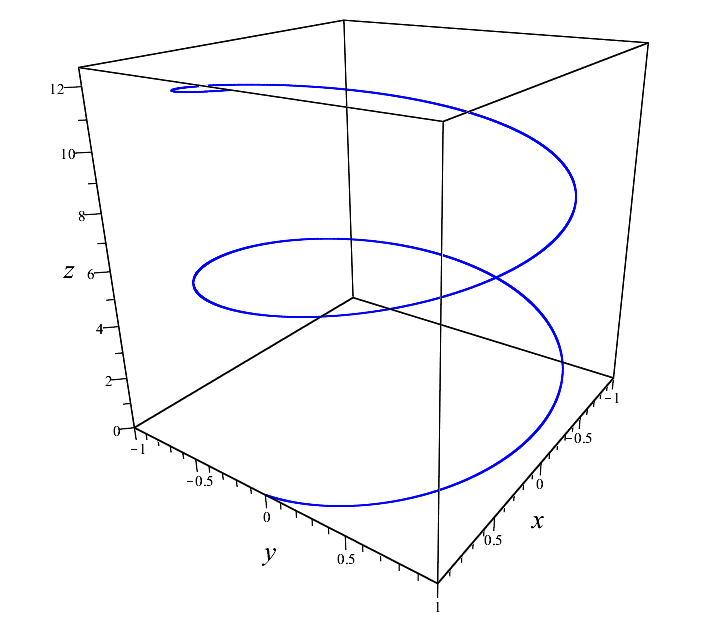
Винтовая линия
Здесь на картинке параметр $inline$t$inline$ пробегает значения от $inline$0$inline$ до $inline$4\pi$inline$. Кстати, предложением ранее, я сказал «некоторую параметризацию». И это неспроста. Потому что параметризаций этой конкретной винтовой линии может быть бесконечно много.
Например, та же самая линия:
\begin{equation*}
\begin{cases}
x = cos (t^{2}),
\\
y = sin (t^{2}),
\\
z = t^{2}
\end{cases}
\end{equation*}
это та же самая винтовая линия, и картинка будет та же самая (не буду еще раз вставлять), правда, $inline$t$inline$ пробегает значения от $inline$0$inline$ до $inline$2\sqrt{\pi}$inline$.
Да и вообще, сделав замену $inline$t = g (\tilde{t})$inline$, это будет всё та же винтовая линия (при условии, что $inline$g (\tilde{t})$inline$ — монотонная):
\begin{equation*}
\begin{cases}
x (\tilde{t}) = cos (g (\tilde{t})),
\\
y (\tilde{t}) = sin (g (\tilde{t})),
\\
z (\tilde{t}) = g (\tilde{t}).
\end{cases}
\end{equation*}
Про параметризации мы еще поговорим дальше, и про особенную параметризацию, называемую «естественной», но уже в следующих статьях (возможно).
Производная и касательный вектор
А сейчас, самое время начать дифференциальный анализ кривых. Не переживайте, определение производной вектора быстро проскочим ;) Итак, вот у нас вектор, зависящий от параметра $inline$t$inline$: $inline$\vec{r}(t) = (x (t), y (t), z (t)).$inline$
Можно записать его разложенным по базису: $inline$\vec{r}(t) = x (t)\vec{i} + y (t)\vec{j} + z (t)\vec{k}$inline$.
А производная, по обычаю, определяется как предел:
$$display$$ \dot{\vec{r}} = \frac{d\vec{r}}{dt} = \lim_{\Delta t\to 0} \frac{\Delta\vec{r}}{\Delta t} = \lim_{\Delta t\to 0} \frac{\vec{r}(t+\Delta t) — \vec{r}(t) }{\Delta t}, $$display$$
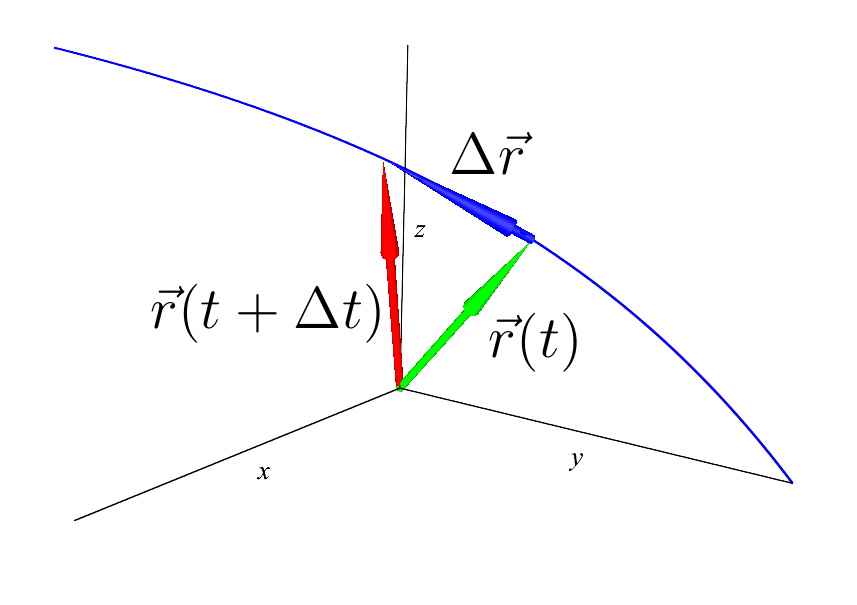
Производная векторной функции (почти)
сам предел векторной функции — это есть пределы каждой из компонент:
\begin{equation*}
\dot{\vec{r}} = \lim_{\Delta t\to 0} \frac{[x (t+\Delta t)\vec{i} + y (t+\Delta t)\vec{j} + z (t+\Delta t)\vec{k}] — [x (t)\vec{i} + y (t)\vec{j} + z (t)\vec{k}] }{\Delta t} = \\
\lim_{\Delta t\to 0} \frac{[x (t+\Delta t)-x (t)]\vec{i} + [y (t+\Delta t)-y (t)]\vec{j} + [z (t+\Delta t)-z (t)]\vec{k}] }{\Delta t} = \\
\lim_{\Delta t\to 0} \frac{x (t+\Delta t)-x (t) }{\Delta t}\vec{i} + \lim_{\Delta t\to 0}… = \\ \dot{x}\vec{i} + \dot{y}\vec{j} + \dot{z}\vec{k} = (\dot{x}, \dot{y}, \dot{z}).
\end{equation*}
Ну и даже на рисунке видно, где $inline$\Delta t$inline$ еще даже к нулю не устремили, что этот вектор $inline$\dot{\vec{r}}$inline$ является касательным к кривой. В теормехе его интерпретируют как скорость и обозначают так:
$$display$$ \dot{\vec{r}} = \vec{v},$$display$$
а саму кривую, соответственно как траекторию движения материальной точки, но мы об этом еще поговорим, потом.
Так вот, этот вектор $inline$\vec{v}$inline$ является касательным к нашей кривой всюду, кроме особых точек (в смысле что в особых точках касательного вектора может и не существовать). Но их так мало, что давайте о них пока даже не будем. И получается, что наш вектор $inline$\vec{v}$inline$ есть как бы базис нашей кривой, показывает куда кривая дальше пойдет. Потому лучше бы его сделать единичным как и все остальные орты. Просто поделим на его длину и обозначим по привычному:
$$display$$ \vec{\tau} = \frac{\vec{v}}{v},$$display$$
теперь то, он всегда равен единице:
$$display$$ \langle \vec{\tau}, \vec{\tau} \rangle = \langle \frac{\vec{v}}{v}, \frac{\vec{v}}{v} \rangle = \frac{\langle \vec{v}, \vec{v} \rangle}{v^{2}} = \frac{v^{2}}{v^{2}} = 1 $$display$$
Вектор нормали
А теперь это равенство можно продифференцировать, ради забавы, как левую так и правую часть (в общем в таких делах, всё что не встретишь, лучше продифференцируй на всякий случай):
$$display$$ \frac{d\langle \vec{\tau}, \vec{\tau} \rangle}{dt} = \frac{d (1)}{dt}, $$display$$
справа понятное дело — ноль. А вот слева мы дифференцируем скалярное произведение векторов. Учитывая правила дифференцирования скалярных, векторных произведений и прочих вещей (которые совершенно не сложно доказать, даже имея в наличии лишь то, что написано выше в этой статье):
$$display$$ \frac{d\langle \vec{a}, \vec{b} \rangle}{dt} = \langle \dot{\vec{a}}, \vec{b} \rangle + \langle \vec{a}, \dot{\vec{b}} \rangle, $$display$$
$$display$$ \frac{d[\vec{a}, \vec{b}]}{dt} = [ \dot{\vec{a}}, \vec{b}] + [\vec{a}, \dot{\vec{b}} ], $$display$$
$$display$$ \frac{d (k\vec{a})}{dt} = \dot{k}\vec{a} + k\dot{\vec{a}}, $$display$$
в последнем выражении $inline$ k = k (t) $inline$ скалярная функция, зависящая от параметра.
Ну теперь то, без проблем закончим дело:
$$display$$ \langle \dot{\vec{\tau}}, \vec{\tau} \rangle + \langle \vec{\tau}, \dot{\vec{\tau}} \rangle = 0, $$display$$
$$display$$ 2 \langle \vec{\tau}, \dot{\vec{\tau}} \rangle = 0, $$display$$
$$display$$ \langle \vec{\tau}, \dot{\vec{\tau}} \rangle = 0, $$display$$
тут еще учли свойство симметричности скалярного произведения, оттуда и двойка вылезла:
$$display$$ \langle \vec{a}, \vec{b} \rangle = \langle \vec{b}, \vec{a} \rangle. $$display$$
Ну всё, теперь можно делать выводы. Последнее скалярное произведение равно нулю. А такое бывает лишь тогда, когда либо хотя бы один из векторов нулевой, либо они перпендикулярны. Так как наш $inline$\vec{\tau}$inline$ совершенно произвольный (мы то зачем все это делаем? Чтобы вычислять касательный вектор абсолютно для любой кривой), то делаем вывод что производный вектор от единичного касательного есть всегда ему перпендикулярен, расположен под углом $inline$ 90^{\circ} $inline$:
$$display$$ \vec{\tau} \perp \dot{\vec{\tau}}. $$display$$
Отлично. Этот производный вектор можно назвать вектором нормали к нашей кривой. Но мы ведь хотим чтобы он был тоже единичным, а это совершенно необязательно на данный момент. Потому просто разделим на его же длину, тогда уж точно никуда не денется:
$$display$$ \vec{n} = \frac{\dot{\vec{\tau}}}{|\dot{\vec{\tau}}|}. $$display$$
Вспоминая что такое $inline$\vec{\tau}$inline$, найдем его производную:
$$display$$ \dot{\vec{\tau}} = \frac{d\vec{\tau}}{dt} = \frac{d}{dt}\left (\frac{\vec{v}}{v}\right), $$display$$
здесь дифференцируемая функция — скаляр умноженный на вектор $inline$ k (t)\vec{v}(t) $inline$, где $inline$ k (t) = \frac{1}{v} = v^{-1} $inline$, тогда:
$$display$$ \frac{d}{dt}\left (\frac{\vec{v}}{v}\right) = \frac{d}{dt}\left (v^{-1}\vec{v}\right) = \frac{d (v^{-1})}{dt}\vec{v} + v^{-1}\frac{d\vec{v}}{dt}. $$display$$
Второе слагаемое понятно:
$$display$$ \frac{d\vec{v}}{dt} = \dot{\vec{v}} = (\ddot{x}, \ddot{y}, \ddot{z}), $$display$$
а с первым сейчас разберемся, просто дифференцируя как сложную функцию:
$$display$$ \frac{d (v^{-1})}{dt} = (-1)v^{-2}\frac{dv}{dt}, $$display$$
здесь $inline$ v = \sqrt{\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2}} = \sqrt{\langle \vec{v}, \vec{v} \rangle} $inline$ — модуль нашего вектора скорости, скалярная функция, потому будем просто дальше дифференцировать её как сложную:
$$display$$ \frac{dv}{dt} = \frac{d\sqrt{\langle \vec{v}, \vec{v} \rangle}}{dt} = \frac{1}{2\sqrt{\langle \vec{v}, \vec{v} \rangle}}\frac{d\langle \vec{v}, \vec{v} \rangle}{dt} = \frac{1}{2v}2\langle \vec{v}, \dot{\vec{v}} \rangle = \dfrac{\langle \vec{v}, \dot{\vec{v}} \rangle}{v}, $$display$$
а теперь всё можно собрать воедино:
$$display$$ \frac{d (v^{-1})}{dt} = (-1)v^{-2}\dfrac{\langle \vec{v}, \dot{\vec{v}} \rangle}{v} = -\dfrac{\langle \vec{v}, \dot{\vec{v}} \rangle}{v^{3}}, $$display$$
и наконец:
$$display$$ \dot{\vec{\tau}} = -\dfrac{\langle \vec{v}, \dot{\vec{v}} \rangle}{v^{3}}\vec{v} + v^{-1}\dot{\vec{v}} = \frac{\dot{\vec{v}}}{v} -\vec{v}\dfrac{\langle \vec{v}, \dot{\vec{v}} \rangle}{v^{3}} = \dfrac{\dot{\vec{v}}v^{2} — \vec{v}\langle \vec{v}, \dot{\vec{v}} \rangle }{v^{3}} = \dfrac{\dot{\vec{v}}\langle \vec{v}, \vec{v} \rangle — \vec{v}\langle \vec{v}, \dot{\vec{v}} \rangle}{v^{3}}. $$display$$
Числитель сильно напоминает формулу «бац минус цаб» — двойного векторного произведения:
$$display$$ \left[ \vec{a}, \left[ \vec{b}, \vec{c} \right] \right] = \vec{b}\langle \vec{a}, \vec{c} \rangle — \vec{c}\langle \vec{a}, \vec{b} \rangle, $$display$$
теперь, если принять $inline$ \vec{b} = \dot{\vec{v}}, \vec{a} = \vec{v}, \vec{c} = \vec{v}: $inline$
$$display$$ \dot{\vec{v}}\langle \vec{v}, \vec{v} \rangle — \vec{v}\langle \vec{v}, \dot{\vec{v}} \rangle = \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right]. $$display$$
Теперь совсем не сложно записать вектор нормали, и всё будет понятно при этом еще:
$$display$$ \vec{n} = \frac{\dot{\vec{\tau}}}{|\dot{\vec{\tau}}|} = \dfrac{\left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] / v^{3}}{\left| \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] \right| /v^{3}} = \dfrac{\left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right]}{\left| \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] \right|}. $$display$$
Вектор бинормали
Вроде бы всё готово, но такое чувство, что чего то не хватает… Наша кривая живет в трехмерном пространстве, где число базисных векторов должно быть 3. Мы же пока получили два перпендикулярных единичных вектора. Ну не вопрос, третий легко получить с помощью векторного произведения первых двух. Причем, он будет перпендикулярен исходным, и плюс еще единичным, так как касательный и нормаль — единичные. Люди до нас его назвали «бинормаль»:
$$display$$ \vec{b} = \left[ \vec{\tau}, \vec{n} \right], $$display$$
но чтобы не травмировать психику тройным векторным произведением, давайте запишем вектор нормали в таком виде:
$$display$$ \vec{b} = \left[ \frac{\vec{v}}{v}, \dfrac{\dot{\vec{v}}v^{2} — \vec{v}\langle \vec{v}, \dot{\vec{v}} \rangle}{\left| \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] \right|} \right] = \dfrac{1}{v\left| \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] \right|}\left (v^{2}\left[ \vec{v}, \dot{\vec{v}} \right] — \langle \vec{v}, \dot{\vec{v}} \rangle\left[ \vec{v}, \vec{v} \right] \right), $$display$$
где второе слагаемое — ноль, ибо векторное произведение вектора самого на себя = 0. А чтобы упростить знаменатель, запишем:
$$display$$ \left| \left[ \vec{v}, \left[ \dot{\vec{v}}, \vec{v} \right] \right] \right| = v\left|\left[ \dot{\vec{v}}, \vec{v} \right] \right|\sin (\phi), $$display$$
где $inline$ \phi = \frac{\pi}{2} $inline$ — угол между векторами $inline$ \vec{v} $inline$ и $inline$ \left[ \dot{\vec{v}}, \vec{v} \right] $inline$. Естественно он прямой, так как вектор $inline$ \left[ \dot{\vec{v}}, \vec{v} \right] $inline$ перпендикулярен своим родителям, если так выразиться.
Итого имеем вектор бинормали:
$$display$$ \vec{b} = \dfrac{v^{2}\left[ \vec{v}, \dot{\vec{v}} \right]}{v^{2}\left|\left[ \dot{\vec{v}}, \vec{v} \right] \right|} = \dfrac{\left[ \vec{v}, \dot{\vec{v}} \right]}{\left|\left[ \vec{v}, \dot{\vec{v}} \right] \right|}. $$display$$
Ну теперь всё, мы с вами получили выражения для вычисления касательного, нормального, и вектора бинормали для произвольной параметризации кривой. Давайте их запишем все вместе:
$$display$$ \vec{\tau} = \frac{\vec{v}}{v},$$display$$
$$display$$ \vec{n} = \dfrac{\left[ \left[ \vec{v}, \dot{\vec{v}} \right], \vec{v} \right]}{\left| \left[ \left[ \vec{v}, \dot{\vec{v}} \right], \vec{v} \right] \right|}, $$display$$
$$display$$ \vec{b} = \dfrac{\left[ \vec{v}, \dot{\vec{v}} \right]}{\left|\left[ \vec{v}, \dot{\vec{v}} \right] \right|}. $$display$$
Тут мы вектор нормали немного отредактировали, чтобы всё было в хорошем тоне. То есть переставили во внутренней скобке вектора, и во внешней. Два раза, потому знак остался прежним.
Пример
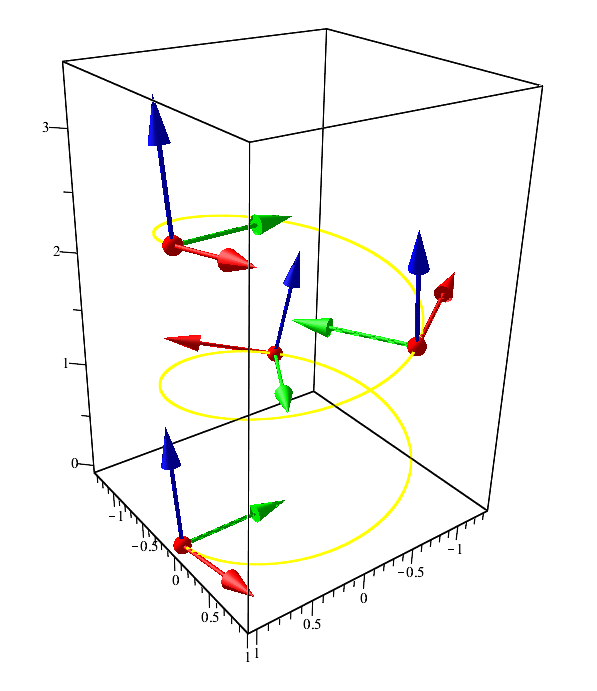
Кривая «винтовая линия» и её вектора: касательный — красный, нормальный — зеленый, бинормальный — синий
Ссылки:
Дифференциальная геометрия кривых
Продолжение, по возможности, следует…
